VAE는 input image와 비슷해지게 Reconstruction term과 샘플링 하기 위한 정규분포가 표준정규분포와 유사하게 만드는 Regularization term이 있다.
이번 포스터에서는 Reconstruction term에서의 Reparameterization trick과
Regularization term에서의 Regularity를 알아보겠다.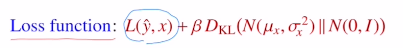
Reparameterization trick
x를 인코더로 넣으면 두 개의 vector를 output으로 꺼낸다.
하나는 평균에 관한 것, 하나는 표준편차에 관한 것이다.
이 평균과 시그마를 나타내는 가우시안 분포에서 랜덤 샘플링을 하게 된다. 그리고 얻은 샘플을 디코더로 보내서 yhat을 구하게 된다.
이렇게 아래와 같이 인코더로 뮤,시그마 분포를 만들고 여기서 qΘ를 따르는 z를 뽑는 random sampling이 진행된다. 이를 디코더로 보내는 것인데, 이 random sampling은 미분을 할 수 없기에 나중 backpropagation이 불가하다.
이 문제를 해결하기 위해 Reparameterization trick을 이용한다.
ε을 N(0,1)에서 뽑고 우리는 N(μ,σ^2)에서 뽑은 것을 원하기에 z = μ + σㆍε(element wise multiplication)로 만들어 이 sample을 사용하게 되는 것이다!
이렇게 되면 기존과 달리 backpropagation을 진행할 때, random sampling하는 곳을 지나지 않게 된다! random component가 분리되기에 역전파를 계산할 때 입실론을 상수로 여겨 무시하게 되는 것이다!
(z = μ + σㆍε를 μ에대해 미분하면 그냥 1이 되고, σ에 대해 미분하면 ε이 나오며 미분이 가능하다.)
이 Reparameterization trick은 VAE뿐만 아니라 Bayesian Deep Learning에서도 핵심 아이디어로 사용되기에 매우 중요하다.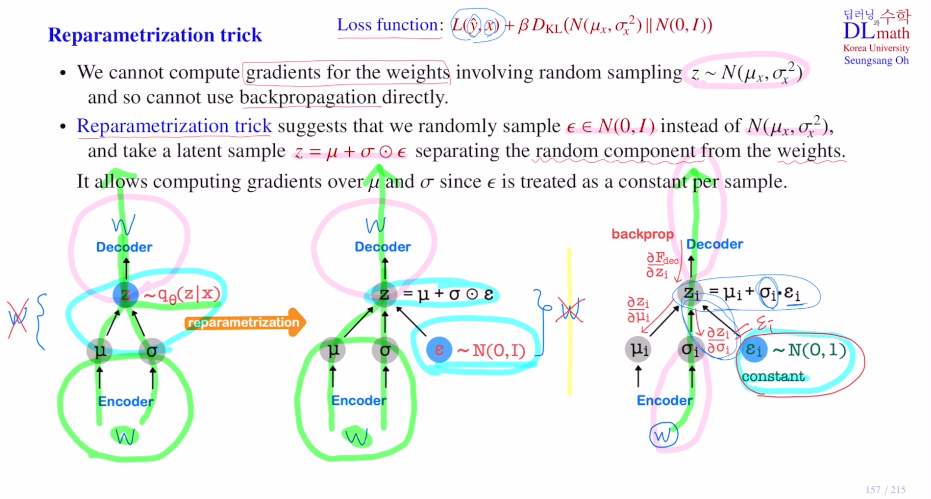
Regularizaiton
latent space가 Regularity를 만족해야 새로운 데이터를 generate 잘 할 수 있게 된다.
두 가지를 만족해야 regularity라고 하는데
첫 번째는 Continuity이다.
아래 latent space를 보면 각 input data에 대해 latent space 내 distribution이 만들어져 있다. 이 latent space 안에 아주 가까운 두 점을 뽑고 이를 디코더를 통해 generate하면 이 reconstructed output이 굉장히 비슷해야 한다는 것이다. 이것이 continuity이다.
하지만 아주 가깝지만 서로 다른 확률분포에 속해 있을 때는 완전히 다른 output이 나오게 된다. 이런 경우는 continuity가 적다고 한다.
두 번째는 Completeness이다.
적당한 한 점을 샘플 z로 뽑았다고 했을 때, 이 z를 Dec(z)로 보내게 될 텐데 이 output이 input data에서 다루는 의미 있는 데이터가 되어야 한다는 것이다. 전혀 다른 이상한 output이 나오면 안 된다는 것이다. 아래를 예시로 들면 흰색 부분과 같이 포함되어 있지 않은 것을 뽑으면 이상한 output이 나오게 되는데 이런 경우는 completeness가 좋지 않은 것이다.
즉! continuity로 서로 가까운 점은 비슷한 것을 generate하고, 확률분포들이 서로 인접하여 아예 다른 이상한 샘플이 뽑히지 안게 completeness를 만족해야 한다는 것이다.
따라서 VAE에서는 이 regularity를 만족시키기 위해 regularization term이 추가된 것이다. 표준정규분포로 만듬으로 Continuity와 Completeness를 만족하게 해준다.
++ covariance matrix to be close to I : 시그마가 1로 간다.
++ 평균은 reconstruction term때문에 0에 가지는 않지만 0에 가깝게 하여 분포들이 서로 가깝게 가게 해준다. 이를 통해 latent space 내 어떤 점을 찍더라도 그것을 표현하는 분포가 존재하여 output이 아름답게 나온다.
아래 그림은 input data에 대한 인코더가 만들어낸 latent space를 나타낸 것이다.
AE의 핵심은 input data에 대해 lower dimensional latent vector를 만드는 것이다. 이는 generative model로는 별로 좋지 않다. 그 이유는 latent space가 irregular하기 때문에 각 데이터마다 값들을 얼마나 수정해야 할지 모르기 때문이다. 아래를 보면 데이터마다 latent space가 얇기도 하고 굵기도 하다. 또한 가까운 데이터는 비슷한 것을 생성해야 하지만 가까이 있어도 각기 아예 다른 것을 만들게 되는 점도 있다. 즉, continuity가 잘 성립되지 않는다.
cluster간 거리도 일정하지 않는다. gap이 있기 때문에 이 사이에 있는 점은 이상한 output을 내보내게 된다. completeness도 없다.
AE는 없이 KL-divergence를 사용하면 분포가 모두 일정하게 바뀌어 데이터들을 구별할 수 없게 된다.
VAE는 이 둘을 합한 것으로 recontruction term과 regularization term이 있어 output도 잘 생성하고, 분포도 서로 가깝고(평균을 0으로 가깝게 하기에) 고르게 해주며(표준편차를 1로) continuity도 만족하고 gap이 없이 completeness도 만족하는 아주 이상적인 latent space를 만들게 된다.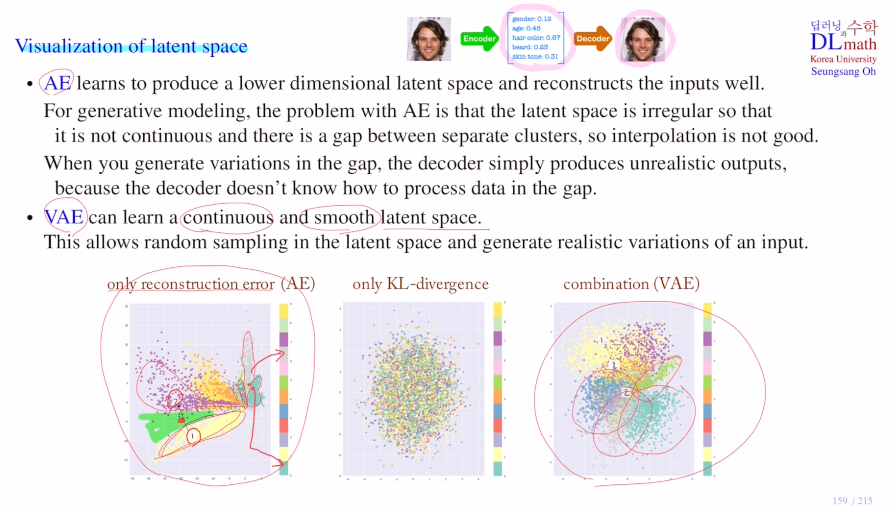
고려대학교 오승상 교수님 딥러닝 강의 : https://www.youtube.com/watch?v=bKzN-k4lMRI&list=PLvbUC2Zh5oJvByu9KL82bswYT2IKf0K1M&index=37
