VAE를 마치고 이제부터는 GAN을 알아보자!
GAN은 Generative Adversarial Network로 생성적 적대 신경망 이다. (비지도 학습)
GAN : Generative Adversarial Nets - 논문 리뷰
을 참고하면 좋을 것 같다.
VAE의 목적은 기존의 데이터에서 확연히 다른 데이터를 만들어 내는 것이 아니라, 하나의 input data를 약간 변형시켜 만든 많은 data들을 생성하는 것이 목적이다. 그렇기에 만들어 낸 데이터가 새로운 데이터이다 라고 말하기는 어렵다.
그에 반해 GAN은 아예 새로운 데이터를 만들어 낸다. 진정한 의미로 새롭게 생성했다고 할 수 있는 것이다.
VAE는 data augnetation처럼 데이터 양을 늘리기 위해서 사용된다면,
GAN은 원래 generative model의 목적과 같이 새로운 데이터를 생성하는 모델이다.
GAN은 생성자와 판별자가 있어 서로가 서로를 적대적으로 생각하며 학습하는 것이다. 이 부분은 목적함수에서 잘 조절하는데 개념을 말한 이후 구체적인 방법을 말해보겠다.
여기서 사용되는 network는 MLP, CNN, RNN, AE, DRL에도 적용할 수 있다.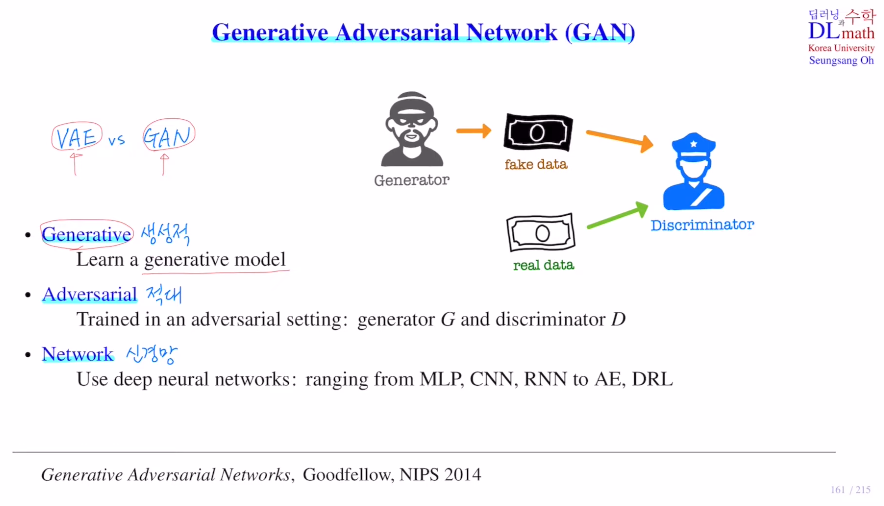
GAN은 2014년에 발표되었고 AI산업에 큰 영향을 미쳤다.
특징1) GAN이전에는 지도학습에 초점이 맞추어져 있었는데, 비지도학습으로 확장되었다.
특징2) GAN 이후 generative model이 활발하게 연구되었고 fake data를 만드는데 real data와 구별하기 굉장히 어려울 정도이다.
특징3) 하지만 training하는 것 자체가 굉장히 어렵다. 그 이유는 non-convergence problem과 mode collapse problem이다.
우선 non-convergence problem을 알아보자. 보통 딥러닝 알고리즘은 loss ft을 정한 후 이 loss ft을 gradient descent 알고리즘으로 minimize시키는 쪽으로 학습한다. iteration을 반복할 수록 loss가 점점 줄어든다. 하지만 GAN에서 사용되는 loss ft은 minimax형태로 되어 있다. 이 minimax는 convergence가 보장되어 있지 않다. 따라서 GAN은 학습할 때 항상 좋은 쪽으로 가는 것이 아니라, 전혀 학습을 하지 못하고 weight parameter들이 엉망이 될 수도 있다는 것이다.
두 번째로 mode collapse problem을 알아보자. MNIST 데이터셋을 학습할 때 생성자가 7을 잘 만들어 판별자가 구분 못 한다면 생성자는 7만 계속 생성해 낸다. 즉, 생성자가 만드는 데이터의 다양성이 떨어지게 된다. 이를 방지하고 다양한 데이터를 만들 수 있게 하는 것은 아주 어려운 문제가 된다.
GAN의 구조에 대하여 알아보자!
GAN은 위에서 설명했듯 Generator network G와 Discriminator network D로 이루어져 있다.
생성자는 noise가 섞인 latent variable z(random variable)를 받게 된다. 이를 생성자가 sample data(fake data) G(z)를 만든다. 그리고 real dataset에서 뽑은 real sample을 x라고 한다면, 판별자 D는 들어오는 데이터가 x : real인지 G(z) : fake인지 (fake)0~1(real)값으로 판별하는 것이다. 이를 통해 loss를 만들고 학습하게 된다.
=> 생성자 G는 판별자 D가 최대한 1을 내보내도록 학습하게 되고, 판별자 D는 최대한 잘 구분할 수 있게 학습하게 된다.
이렇게 적대적으로 한다. 하지만 서로가 서로를 이기기 위해 성장하며 서로 같이 성장하게 된다.
경쟁적이면서도 서로 돕는다.
여기서 어려운 점은 서로 적대적이기에 학습을 진행할 때 loss ft을 잡기 어렵다.
동시에 학습할 수 없기에, 판별자 D를 학습할 때는 생성자 G의 파라미터들을 고정시키고 업데이트를 하지 않은 상태에서 판별자만 학습을 진행한다.
이후 어느 정도 지나면, 판별자를 고정시키고 생성자만 weight update를 진행하며 학습을 하게 된다.
이것을 계속해서 반복하며 서로의 성능이 점점 좋아지게 된다!
그 후 GAN의 최종 목적인 새로운 데이터를 생성하는 것을 위해 학습을 마친 후에는 생성자만을 통해 많은 새로운 데이터를 생성하게 된다.
(판별자는 오직 생성자를 학습시키기 위해 사용된 것이다.)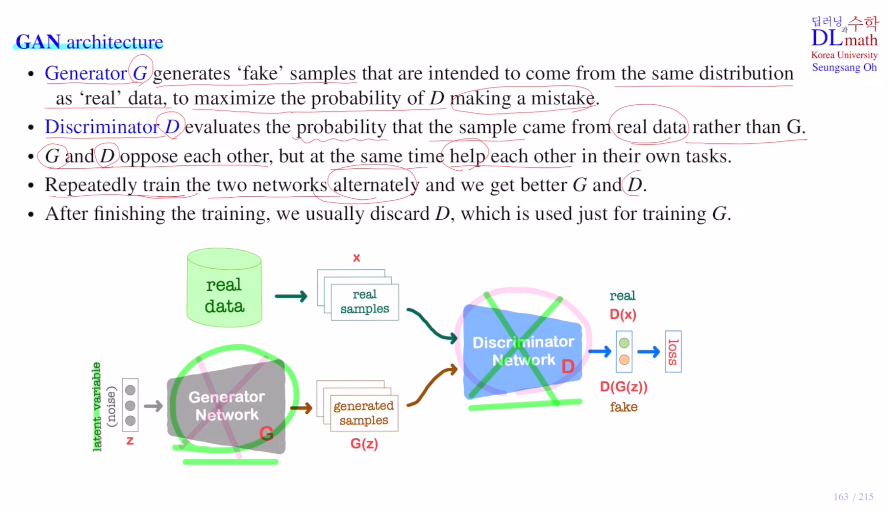
이제 GAN network를 학습하기 위한 Object function(loss ft과 똑같은데 GAN에서는 minimize도 하지만 maximize도 하기에 이렇게 부른다.)을 알아보자.
이 전체 값에 대해서 생성자는 minimize시키고 판별자는 maximize를 한다.
pdata(x)는 real data의 분포로 x는 이 real data분포를 따른다는 것이다.
pz(z)는 latent variable로 주로 uniform or normal 분포가 된다.
D()는 판별자가 들어온 값이 real인지 fake인지 구분하는 것으로 판별자의 입장에서는 D(x)는 1로, D(G(z))는 0으로 판단하는 것이 좋다. 그렇기에 전체 값이 maximize시키는 쪽으로 학습시키는 것이다.
반대로 생성자 입장에서는 왼쪽은 G가 없기에 오른쪽만 사용하면 된다. G는 오른쪽 식의 D(G(z))를 최대한 1로 만들어 전체적인 값을 낮추는 것을 목표로 학습하게 된다.
결국 동일한 object ft을 두고 two player가 minimax ploblem을 실행하는 것이다.
이 solution은 Nash equilibrium인데, 이는 real data의 분포와 fake data의 분포가 동일하게 될 때 Nash equilibrium라고 한다.(D=1/2이라는 것은 찍는 다는 것으로 아주 좋은 생성자이다.)
위에서 말한 내쉬 균형을 알아보자.
경제학의 게임이론에서 배웠던 내용이기에 반갑다.
어떤 플레이어도 그 이상 좋은 선택을 할 수 없는 것으로, 한 플레이어가 선택할 때 다른 플레이어는 고정되어 있다고 가정하고 진행한다.
게임에 따라 균형이 많을 수도 없을 수도 있다.
Saddle model에 적용해 보자. player A는 x쪽, player B는 y쪽이라고 할 때,
min(A)max(B) L(A,B) = x^2 - y^2 문제를 풀어보자.
여기서는 유니크 내쉬 균형 x=y=0이 나오며 이 곳은 안장점 saddle point가 된다.
이렇게 minimax problem 에서 solution은 pdata=pg가 되는 것이다.
고려대학교 오승상 교수님 딥러닝 강의 : https://www.youtube.com/watch?v=TYixl1I-QEo&list=PLvbUC2Zh5oJvByu9KL82bswYT2IKf0K1M&index=38
