저번 포스터에서 GAN의 구조와 어떻게 학습할지, 최종적으로 내쉬 균형에 의해 D=1/2이 되는 것 등을 알아보았다.
이번 포스터에서 구체적으로 수식과 함께 알아보자!
우선 Discriminator를 학습하는 것을 확인해보자.
생성자는 고정시켜놓고 학습하지 않는다.
gradient ascent(object ft의 maximize를 위해)를 수행하기 위해 Mini batch가 m이라고 할 때, real data xi m개와 fake data zi m개를 가져온다.
총 2m개의 data를 판별자의 input으로 사용하는 것이다.
이를 통해 생성자는 gradient를 계산하지 않고 판별자에 대해서만 gradient 를 계산하여 파라미터를 업데이트 시킨다.
(backpropagation은 빨간 선까지만 한다!)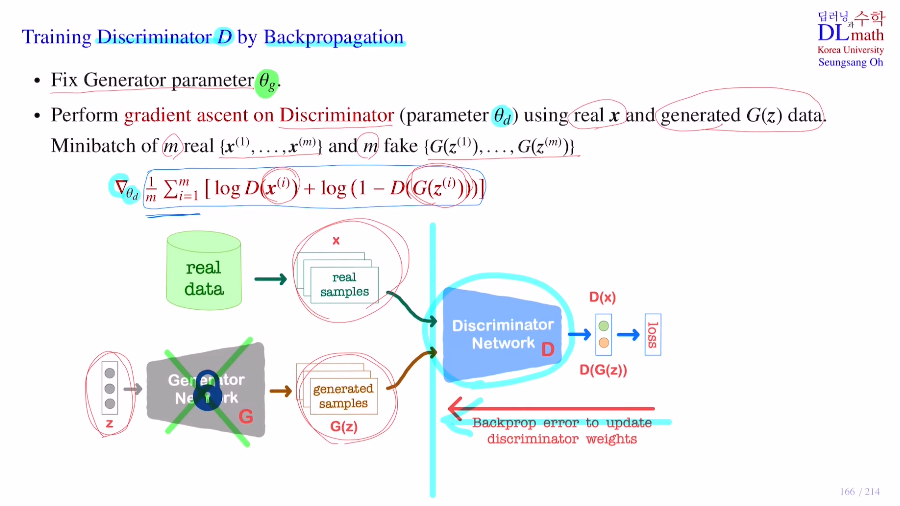
다음으로는 Generator를 학습하는 것을 확인해보자.
이번에는 판별자의 파라미터들을 고정시키고 업데이트 하지 않는다!
생성자는 random variable z를 받는데, 이 z는 N(0,1) or U(-1,1)에서 가져올 수 있다.
생성자에서는 real data는 필요없기에 object ft의 뒷 부분만 가져온다.
이를 통해 generator의 파라미터에 대해서만 gradient 를 계산하고 weight update를 진행하게 된다. 이번에는 minimize를 위해 gradient descent를 사용한다.
식은 아래와 같이 두 가지 종류가 있다. 둘 다 같은 목적을 가지고 있다.
오른쪽이 유용한 경우가 있는데, 생성자가 보통 더 학습하기 어렵다. 학습 초반에는 생성자 성능이 좋지 않아 판별자는 생성자가 만든 데이터를 쉽게 가짜라고 판단한다. 그렇기에 보통 D(G(z))=0으로 많이 출력할 텐데 아래의 경우 초록색 선이 gradient를 계산하면 훨씬 빠른 속도로 minimum에 다가갈 수 있게 해주는 것이다. 따라서 학습 초반에는 오른쪽 식을 주로 사용한다.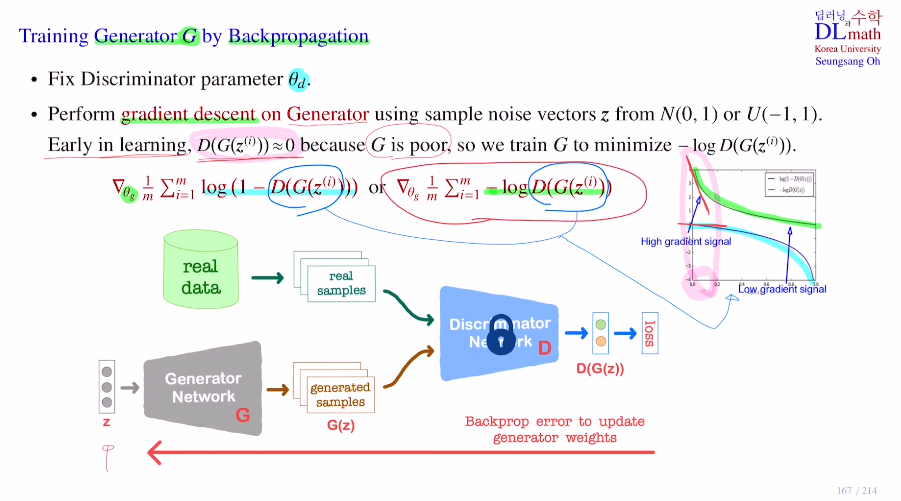
아래는 GAN의 수도코드이다.
판별자와 생성자는 따로 업데이트하기로 했기에 구분되어 있다.
목적함수도 마찬가지로 따로 구분되어 있다.
아래는 GAN 논문에서 소개된 그림으로 optimal로 가는 과정을 나타낸 것이다.
검정 : real data 분포
실선 : fake data 분포
Uniform 분포에서 sample z를 만들어 낼 때 치우치지 않고 중심으로 가는 것이 real data 분포를 따르게 된다.
첫 번째 그림을 보면 판별자가 아직 완전히 학습되지 않았기에 대충 맞기는 하지만 들쭉날쭉하다.
두 번째는 생성자를 고정시키고 판별자를 학습한 것이다. 판별자가 학습하며 점점 optimal 한 값으로 가게 된다. 그것은 D 이며 아래 수식과 같다. 그림에서 만나는 지점은 딱 1/2이 된다. pdata=pg라고 하면 1/2이 되기에. 그 지점을 기준으로 왼쪽은 real data가 더 많기에 D 가 점점 커지므로 판별자의 값이 점점 커진다. 또한 오른쪽은 fake data가 더 많기에 D* 가 점점 작아지므로 판별자의 값이 점점 0으로 간다. 따라서 생성자를 고정시키고(fake data고정) 판별자를 학습시킨다면, 두 번째 그림과 같이 스무스한 판별자값이 나오게 된다.
세 번째는 판별자를 고정시키고 생성자를 학습시키는 것으로 판별자가 fake data를 1에 가깝게 도출해내도록 fake data의 분포를 중심으로 이동시키는 것이다.
이렇게 되면 판별자는 다시 첫 번째 그림과 같이 들쭉날쭉 부정확해진다.
이 세 싸이클을 반복적으로 진행하면 결국 fake data의 분포가 real data의 분포와 같게 되어 결국 둘 다 업데이트를 하지 않게 되어 D=1/2이 된다. 결국 판별자는 찍게 된다.
이 Global optimality : pdata= pg인 내쉬균형을 수학적인 방법으로 알아보자.
G를 고정시키고 maximal D가 D = pdata/(pdata+pg) 인지 증명해보자.
우선 목적함수에서 평균을 적분형태로 표현하고 g(z)를 x로 놓아보자. 그렇게 한 후 이를 극대화시키는 것을 찾는 것인데 alog(y)+blog(1-y)의 maximum값은 미분에 의해 y=a/(a+b) in [0,1] 이 된다. 따라서 G가 고정되어있을 때, D를 maximize시키는 값은 D = pdata/(pdata+pg)이 되는 것이다.
이번에는 위와 같은 값으로 고정해놓고 G를 minimize시켜보자.
이번에는 목적함수에서 logD(x)->log(D* = pdata/(pdata+pg))로 바뀌었다. 그 상태에서 식을 조정해주고 KL발산 식을 이용하면 아래와 같이 바꿀 수 있다.
그 후 KL div의 특징인 항상0보다 크거나 같음, P,Q 순서 바꾸기 불가능(not symmetric), q가0으로 감에 따른 무한대 발산이 있기에,
Jensen-Shannon div를 사용하여 항상 0보다 크거나 같고, 순서바꿀 수 있고, 무한대 발산이 없게 하여 아래와 같이 바꾼다. 이것을 minimum을 갖게 하기 위해서는 0이 되는 값 P=Q일 때이다. 즉, pdata=pg일 때인 것이다.
D와 G가 충분히 수용력이 있어 성능이 계속 올라갈 수 있다면, D가 optimal D* 에 도달을 하고, 그 optimal 한 값을 기준으로 해서 G가 업데이트를 하여 fake data의 분포가 점점 좋아지고, 결국 이를 반복하면 fake data의 분포가 real data의 분포로 converge하게 되는 것이다.
이것이 GAN의 핵심적인 수학적 이론이다.

고려대학교 오승상 교수님 딥러닝 강의 : https://www.youtube.com/watch?v=a5tfIt-WMGw&list=PLvbUC2Zh5oJvByu9KL82bswYT2IKf0K1M&index=39
