Part1. 머신러닝

ch3. 분류

1. image 데이터 확인

%matplotlib inline
import matplotlib as mpl
import matplotlib.pyplot as plt

some_digit = X[0]
some_digit_image = some_digit.reshape(28, 28)
plt.imshow(some_digit_image, cmap=mpl.cm.binary)
plt.axis("off")

plt.show()

2. 교차 검증에 관하여

cross_val_score:
cross_val_score 함수는 간단한 교차 검증을 수행하기 위해 사용됩니다. 주어진 모델과 데이터에 대해 K-폴드 교차 검증을 수행하고, 각 폴드에서 모델의 성능을 평가하여 평균 성능을 반환합니다. 이 함수를 사용하면 간단하게 교차 검증을 수행할 수 있으며, 모델의 성능을 평가하거나 다양한 모델 간 성능을 비교하는 데 유용합니다. cross_val_score 함수는 내부적으로 KFold 교차 검증을 수행합니다.

StratifiedKFold:
StratifiedKFold는 KFold의 변형으로, 클래스 분포가 고려된 계층화된 샘플링을 제공합니다. 이 함수는 분류 문제에서 클래스의 분포를 유지하면서 교차 검증을 수행합니다. 클래스 불균형이 있는 데이터셋에서 모델을 평가할 때 유용하며, 각 폴드에서 훈련 및 검증 세트의 클래스 비율이 원본 데이터셋의 클래스 비율과 유사하도록 보장합니다. 이로써 모델이 각 클래스의 성능을 더 정확하게 평가할 수 있습니다.

=> 요약하면, cross_val_score는 모델의 성능 평가를 위해 간단한 교차 검증을 수행하는 함수이며, StratifiedKFold는 클래스 불균형을 고려하여 계층화된 샘플링을 사용하여 교차 검증을 수행하는 함수입니다.

1) cross_val_score

from sklearn.model_selection import cross_val_score
cross_val_score(sgd_clf, X_train, y_train_5, cv=3, scoring="accuracy")

2) StratifiedKFold

from sklearn.model_selection import StratifiedKFold
from sklearn.base import clone

skfolds = StratifiedKFold(n_splits=3, shuffle=True, random_state=42)

for train_index, test_index in skfolds.split(X_train, y_train_5):
    clone_clf = clone(sgd_clf)
    X_train_folds = X_train[train_index]
    y_train_folds = y_train_5[train_index]
    X_test_fold = X_train[test_index]
    y_test_fold = y_train_5[test_index]

    clone_clf.fit(X_train_folds, y_train_folds)
    y_pred = clone_clf.predict(X_test_fold)
    n_correct = sum(y_pred == y_test_fold)
    print(n_correct / len(y_pred))

3. Confusion matrix

cross_val_predict를 바탕으로 혼동행렬 구성

from sklearn.model_selection import cross_val_predict

y_train_pred = cross_val_predict(sgd_clf, X_train, y_train_5, cv=3)

---

from sklearn.metrics import confusion_matrix

confusion_matrix(y_train_5, y_train_pred)

4. 정밀도 재현율 curve

• 정밀도/재현율 trade-off
  정밀도 : 무조건 걸러야 하는 (어린아이 맞춤 동영상)
  재현율 : 틀리더라도 최대한 (좀도둑 CCTV)
  -> 임계값에 따라 값을 내리면 재현율이 높아지고 정밀도가 낮아지고, 올리면 재현율이 낮아지고 정밀도가 높아지고.

from sklearn.metrics import precision_recall_curve

precisions, recalls, thresholds = precision_recall_curve(y_train_5, y_scores)

---

def plot_precision_recall_vs_threshold(precisions, recalls, thresholds):
    plt.plot(thresholds, precisions[:-1], "b--", label="Precision", linewidth=2)
    plt.plot(thresholds, recalls[:-1], "g-", label="Recall", linewidth=2)
    plt.legend(loc="center right", fontsize=16) # Not shown in the book
    plt.xlabel("Threshold", fontsize=16)        # Not shown
    plt.grid(True)                              # Not shown
    plt.axis([-50000, 50000, 0, 1])             # Not shown



recall_90_precision = recalls[np.argmax(precisions >= 0.90)]
threshold_90_precision = thresholds[np.argmax(precisions >= 0.90)]


plt.figure(figsize=(8, 4))                                                                  # Not shown
plot_precision_recall_vs_threshold(precisions, recalls, thresholds)
plt.plot([threshold_90_precision, threshold_90_precision], [0., 0.9], "r:")                 # Not shown
plt.plot([-50000, threshold_90_precision], [0.9, 0.9], "r:")                                # Not shown
plt.plot([-50000, threshold_90_precision], [recall_90_precision, recall_90_precision], "r:")# Not shown
plt.plot([threshold_90_precision], [0.9], "ro")                                             # Not shown
plt.plot([threshold_90_precision], [recall_90_precision], "ro")                             # Not shown
save_fig("precision_recall_vs_threshold_plot")                                              # Not shown
plt.show()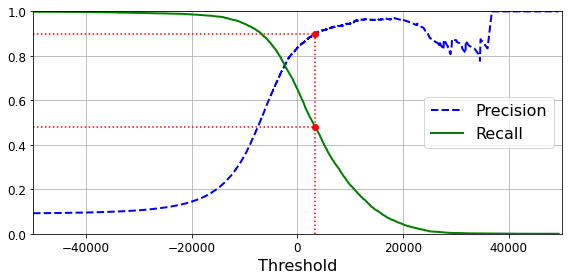

def plot_precision_vs_recall(precisions, recalls):
    plt.plot(recalls, precisions, "b-", linewidth=2)
    plt.xlabel("Recall", fontsize=16)
    plt.ylabel("Precision", fontsize=16)
    plt.axis([0, 1, 0, 1])
    plt.grid(True)

plt.figure(figsize=(8, 6))
plot_precision_vs_recall(precisions, recalls)
plt.plot([recall_90_precision, recall_90_precision], [0., 0.9], "r:")
plt.plot([0.0, recall_90_precision], [0.9, 0.9], "r:")
plt.plot([recall_90_precision], [0.9], "ro")
save_fig("precision_vs_recall_plot")
plt.show()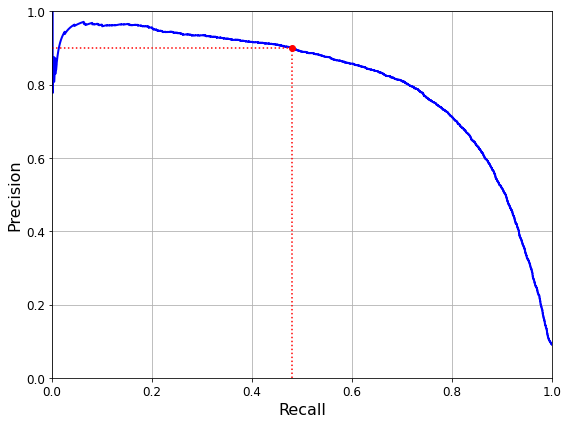

5. Roc curve

재현율과 1-특이도의 그래프로 점선에서 멀리 떨어져 있을 수록 좋은 분류기 입니다.
그래프 아래 면적이 1이면 완벽한 분류기이며, 여기서도 trade-off가 존재합니다.

from sklearn.metrics import roc_curve

fpr, tpr, thresholds = roc_curve(y_train_5, y_scores)

---


def plot_roc_curve(fpr, tpr, label=None):
    plt.plot(fpr, tpr, linewidth=2, label=label)
    plt.plot([0, 1], [0, 1], 'k--') # dashed diagonal
    plt.axis([0, 1, 0, 1])                                    # Not shown in the book
    plt.xlabel('False Positive Rate (Fall-Out)', fontsize=16) # Not shown
    plt.ylabel('True Positive Rate (Recall)', fontsize=16)    # Not shown
    plt.grid(True)                                            # Not shown

plt.figure(figsize=(8, 6))                                    # Not shown
plot_roc_curve(fpr, tpr)
fpr_90 = fpr[np.argmax(tpr >= recall_90_precision)]           # Not shown
plt.plot([fpr_90, fpr_90], [0., recall_90_precision], "r:")   # Not shown
plt.plot([0.0, fpr_90], [recall_90_precision, recall_90_precision], "r:")  # Not shown
plt.plot([fpr_90], [recall_90_precision], "ro")               # Not shown
save_fig("roc_curve_plot")                                    # Not shown
plt.show()

---

from sklearn.metrics import roc_auc_score

roc_auc_score(y_train_5, y_scores)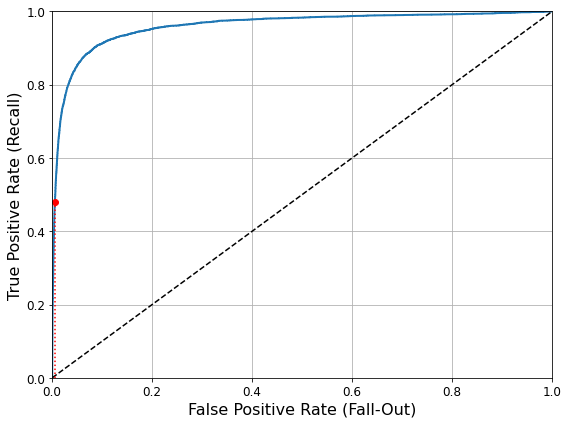

6. 에러 분석

y_train_pred = cross_val_predict(sgd_clf, X_train_scaled, y_train, cv=3)
conf_mx = confusion_matrix(y_train, y_train_pred)
conf_mx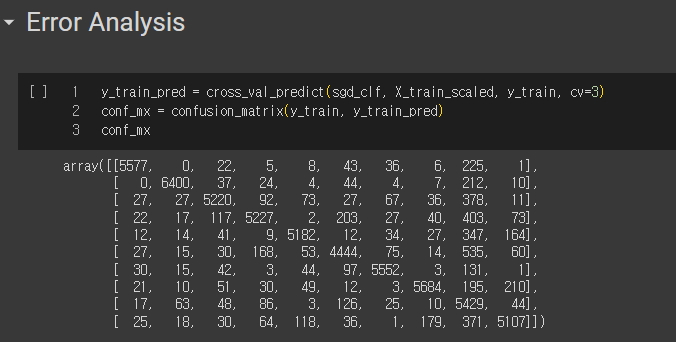

# since sklearn 0.22, you can use sklearn.metrics.plot_confusion_matrix()
def plot_confusion_matrix(matrix):
    """If you prefer color and a colorbar"""
    fig = plt.figure(figsize=(8,8))
    ax = fig.add_subplot(111)
    cax = ax.matshow(matrix)
    fig.colorbar(cax)
    
---

plt.matshow(conf_mx, cmap=plt.cm.gray)
save_fig("confusion_matrix_plot", tight_layout=False)
plt.show()

주대각선이 밝은 것으로 보아 성능이 나쁘지 않음을 확인할 수 잇습니다.

• 주대각선만 0으로 채워 그래프를 확인

row_sums = conf_mx.sum(axis=1, keepdims=True)
norm_conf_mx = conf_mx / row_sums

---

np.fill_diagonal(norm_conf_mx, 0)
plt.matshow(norm_conf_mx, cmap=plt.cm.gray)
save_fig("confusion_matrix_errors_plot", tight_layout=False)
plt.show()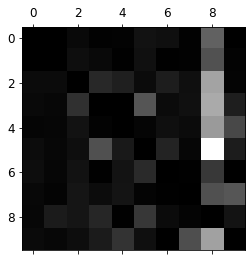

클래스의 8열이 상당히 밝으므로, 8로 잘못 분류되는 것을 줄이도록 개선할 필요가 있습니다.
예를 들어 8처럼 보이는(하지만 8이 아닌) 숫자의 훈련 데이터를 더 많이 모아서 실제 8과 구분하도록 분류기를 학습시킬 수 있습니다.

8. 다중 레이블 분류

단순하게 기존 분류는 y의 dim=1이었다면, 이번에는 concat하는 것 입니다.

from sklearn.neighbors import KNeighborsClassifier

y_train_large = (y_train >= 7)
y_train_odd = (y_train % 2 == 1)
y_multilabel = np.c_[y_train_large, y_train_odd]

knn_clf = KNeighborsClassifier()
knn_clf.fit(X_train, y_multilabel)

---

knn_clf.predict([some_digit])

-> 결과 : array([[False, True]])

숫자 5는 "크지 않고, 홀수" 라고 결과가 나왔습니다!

• 평가는 어떻게 할까요?
  적절한 지표는 많지만 예를 들어 F1 score의 평균을 통해 정하는 방법이 있습니다.
  여기에서는 가중치를 주지 않았지만, 지지도(target label에 속한 샘플 수)를 통해 가중치를 줄 수도 있습니다.

y_train_knn_pred = cross_val_predict(knn_clf, X_train, y_multilabel, cv=3)
f1_score(y_multilabel, y_train_knn_pred, average="macro")