핸즈온 머신러닝

Part1. 머신러닝 ch8. 차원 축소

1. 차원의 저주 Curse of dimensionality

데이터 양에 비해 특성이 너무 많다면 훈련을 느리게 할 뿐 아니라, 좋은 솔루션을 찾기 어려워 집니다. 이러한 문제를 차원의 저주 : Curse of Dimensionality라고 합니다.

차원이 늘어남에 따라 데이터들의 거리들이 늘어납니다. 이는 새롭게 들어오는 샘플 데이터 또한 훈련 샘플과 멀리 떨어져 있을 가능성이 높다는 의미인데, 이 경우 예측이 불안정하게 됩니다.

이러한 문제를 해결하기 위해 데이터의 양을 충분히 늘려 훈련 샘플들의 밀도가 높아지게 하는 방법이 있습니다. 하지만 차원이 너무 큰 경우에는 데이터의 양을 굉장히 많이 증가시켜야 합니다.

두 번째 방법은 차원 축소입니다. 차원축소를 진행하는데 이점들을 살펴보겠습니다.
우선 차원축소를 통해 위에서 언급한 차원의 저주 문제를 해결할 수 있습니다. 또한 2,3차원으로 줄임으로 데이터 시각화를 통해 중요한 통찰을 얻을 수 있고, 판단에 대한 근거를 설명하는데 용이합니다.

2. 차원 축소를 위한 접근 방법

차원 축소는 데이터의 차원을 줄이는 과정입니다. 데이터의 차원이 높을수록 데이터를 이해하고 처리하기 어려워집니다. 따라서 차원 축소는 데이터 분석, 머신 러닝, 컴퓨터 비전 등 다양한 분야에서 활용되고 있습니다.

차원 축소 접근법은 크게 두 가지로 나눌 수 있습니다.

투영(projection) 접근법은 고차원 데이터를 저차원 공간으로 투영하는 방법입니다. 투영은 데이터의 분산을 보존하는 것을 목표로 합니다. 대표적인 투영 알고리즘으로는 주성분 분석(PCA), 카이제르-라이트리히-매뉴엘(KLM) 등이 있습니다.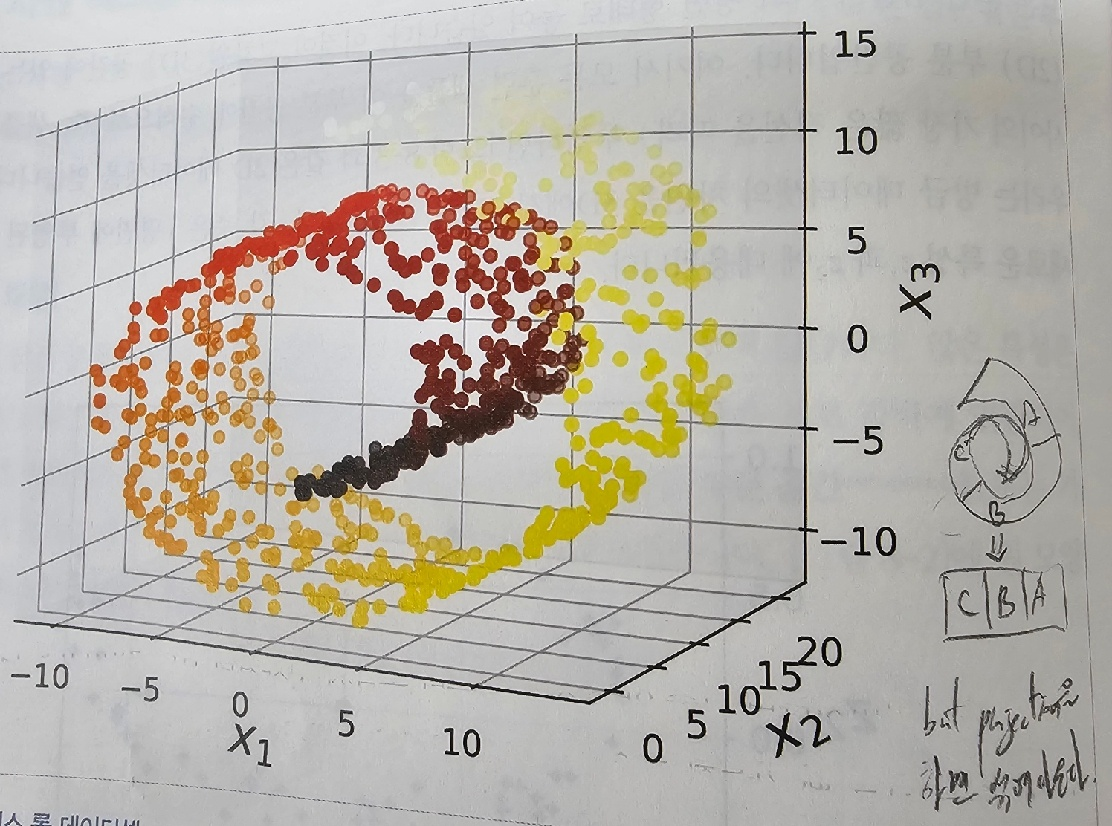

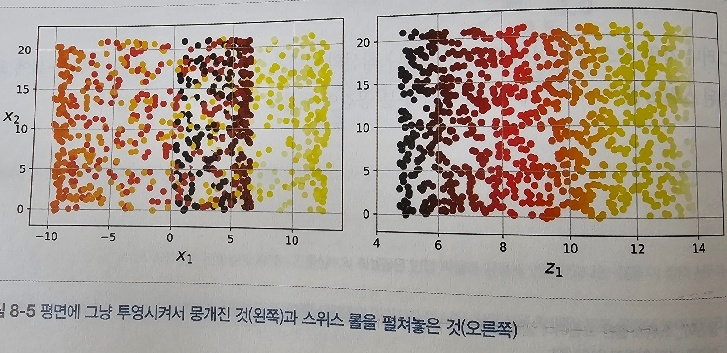
매니폴드 학습(manifold learning) 접근법은 고차원 데이터가 매니폴드(manifold) 위에 있다고 가정하고, 매니폴드를 저차원 공간으로 매핑하는 방법입니다. 매니폴드 학습은 데이터의 구조를 보존하는 것을 목표로 합니다. 대표적인 매니폴드 학습 알고리즘으로는 지역 선형 임베딩(LLE), t-SNE 등이 있습니다.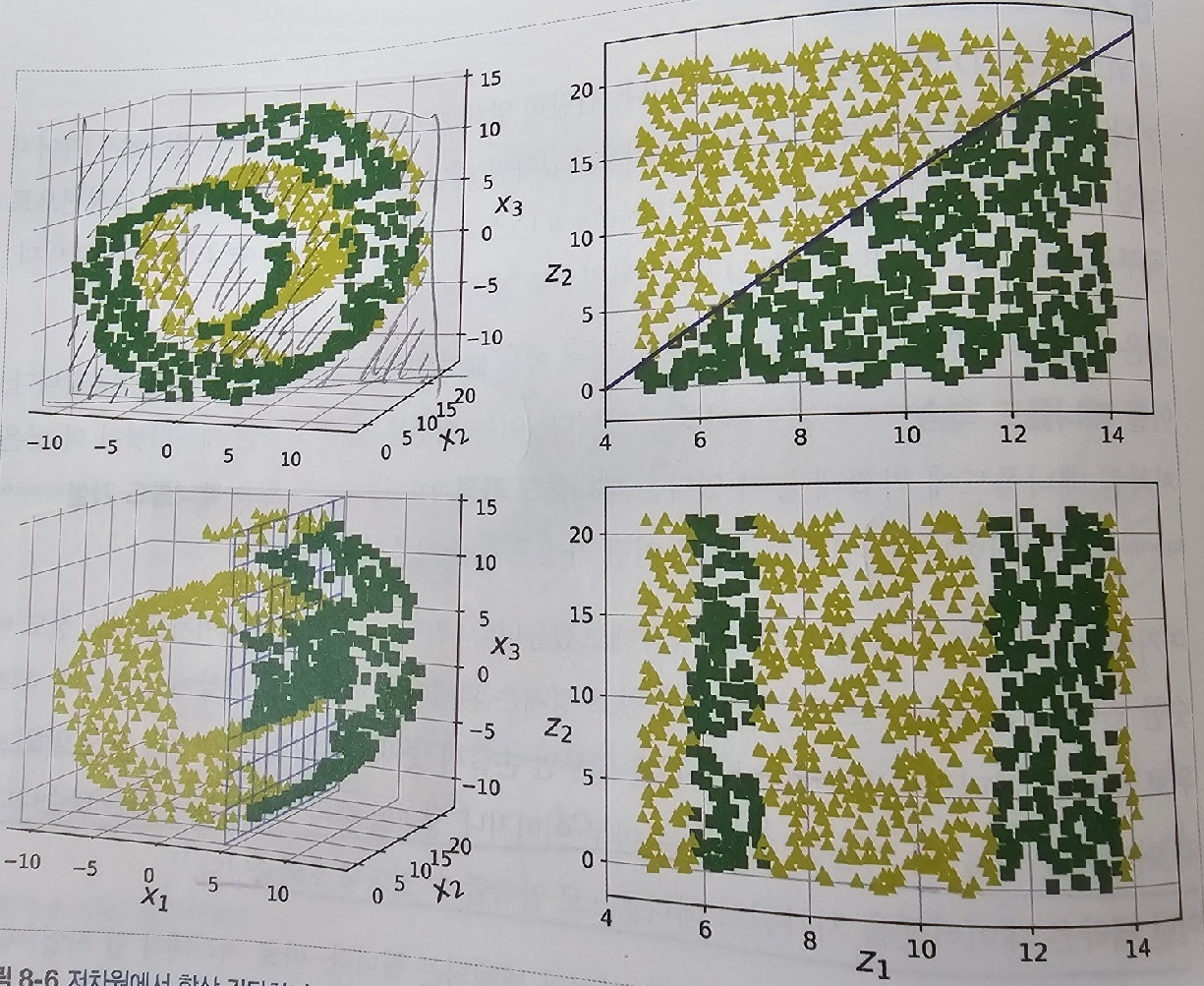

투영 접근법

투영 접근법은 고차원 데이터의 분산을 보존하는 것을 목표로 합니다. 분산은 데이터의 다양성을 측정하는 지표입니다. 데이터의 분산을 보존하면 데이터의 구조를 잘 보존할 수 있습니다.

주성분 분석(PCA)은 투영 접근법의 대표적인 알고리즘입니다. PCA는 데이터의 분산을 가장 큰 차원부터 차례대로 설명하는 차원을 선택합니다. PCA는 데이터의 분산을 최대한 보존하면서 데이터의 차원을 줄일 수 있습니다.

카이제르-라이트리히-매뉴엘(KLM)은 PCA와 유사한 알고리즘입니다. KLM은 PCA와 달리 데이터의 분산을 가장 작은 차원부터 차례대로 설명하는 차원을 선택합니다. KLM은 데이터의 분산을 최소한으로 보존하면서 데이터의 차원을 줄일 수 있습니다.

매니폴드 학습

매니폴드 학습은 고차원 데이터가 매니폴드 위에 있다고 가정하고, 매니폴드를 저차원 공간으로 매핑하는 방법입니다. 매니폴드 학습은 데이터의 구조를 보존하는 것을 목표로 합니다.

지역 선형 임베딩(LLE)은 매니폴드 학습의 대표적인 알고리즘입니다. LLE는 각 데이터 포인트의 가장 가까운 이웃을 사용하여 데이터의 구조를 학습합니다. 그런 다음 학습된 구조를 저차원 공간으로 매핑합니다.

t-SNE는 매니폴드 학습의 또 다른 대표적인 알고리즘입니다. t-SNE는 데이터 포인트의 밀도를 사용하여 데이터의 구조를 학습합니다. 그런 다음 학습된 구조를 저차원 공간으로 매핑합니다.

투영 접근법과 매니폴드 학습의 차이점

투영 접근법과 매니폴드 학습은 모두 차원 축소를 위한 방법이지만, 다음과 같은 차이점이 있습니다.

목표: 투영 접근법은 데이터의 분산을 보존하는 것을 목표로 하지만, 매니폴드 학습은 데이터의 구조를 보존하는 것을 목표로 합니다.
가정: 투영 접근법은 데이터가 고차원 공간에서 선형으로 분포되어 있다고 가정하지만, 매니폴드 학습은 데이터가 고차원 공간에서 비선형으로 분포되어 있다고 가정합니다.
적용: 투영 접근법은 데이터의 분산을 보존해야 하는 경우에 적합하지만, 매니폴드 학습은 데이터의 구조를 보존해야 하는 경우에 적합합니다.
결론

차원 축소 접근법은 데이터의 차원을 줄여 데이터를 이해하고 처리하기 쉽게 만드는 데 도움이 됩니다. 투영 접근법과 매니폴드 학습은 모두 차원 축소를 위한 방법이지만, 각각의 장단점이 있으므로 데이터의 특성에 따라 적절한 방법을 선택해야 합니다.