3. PCA
PCA는 주성분 분석이라고 부르며, 분산이 가장 큰 component를 찾고, 그 principal component를 기반으로 orthogonal한 축 중 다시 한 번 분산을 최대로 보존하는 것을 찾아 나가는 것 입니다.
이를 통해 데이터의 분산을 최대한으로 보존하며 차원을 축소시켜 curse of dimensionality를 막을 수 있게 됩니다.
쉽게 말해 n개의 데이터가 주어졌을 때, nxn 공분산 행렬에서 결국 축을 바꾸어도 전체 합은 유지되기에 축을 변경해 나가며 분산이 큰 순으로 matrix의 diagonal에 적어 나가고, 이 중 일정 threshold를 넘지 못하는 값 혹은 앞에서 부터의 누적합 을 통해 principal component 몇 개만 남겨 차원 축소를 진행하게 됩니다.
Q. 그렇다면 분산을 왜 최대호 보존되는 축을 선택해야 할까요?
이것이 데이터의 정보가 가장 적게 손실되므로 합리적이기 때문입니다.
Q. 이 주성분은 어떻게 찾을 수 있을까요?
바로 singular value decomposition을 통해 훈련 data set 을 세 개의 행렬의 곱으로 표현하고 X=U∑VT (m,m)(m,n)(n,n)(m:샘플개수,n:특성개수)의 V(주성분)에서 원하는 만큼의 단위 벡터를 추출할 수 있습니다.
PCA는 데이터 셋의 평균이 0이라고 가정하기에 sklearn.decomposition import PCA를 쓰지 않고 직접 구현할 경우에는 아래와 같이 평균을 0으로 맞춰주어야 합니다!
X_centered = X - X.mean(axis=0)
U, s, Vt = np.linalg.svd(X_centered)
c1 = Vt.T[:, 0]
c2 = Vt.T[:, 1]
# d차원으로 축소
W2 = Vt.T[:, :2]
X2D = X_centered.dot(W2)아래는 바로 사이킷런에서 PCA사용 코드입니다. 별도의 평균을 빼는 작업이 필요 없습니다!
from sklearn.decomposition import PCA
pca = PCA(n_components=2)
X2D = pca.fit_transform(X)직접 구현과 시이킷런 이용 방법은 같은 값이 나오지만 축이 반대로 바뀌는 정도의 차이가 있을 수 있습니다.(부호 반대)
그렇다면 복원은 어떻게 할까요?
X3D_inv = pca.inverse_transform(X2D)
# SVD 방식의 역변환
X3D_inv_using_svd = X2D_using_svd.dot(Vt[:2, :])위와 같이 pca.inverse를 사용할 수 있지만, 일부 정보를 잃어버리기에 완전히 원본 데이터와 같지는 않습니다.
np.allclose(X3D_inv, X)
=> False
# 재구성 오차
np.mean(np.sum(np.square(X3D_inv - X), axis=1))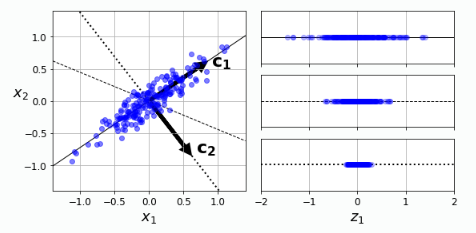
이제 PCA를 계산하는 방법을 알았습니다. 그렇다면 적절한 차원의 수는 어떻게 선택할까요?
PCA로 fit을 진행한 후 pca.explainedvariance_ratio 를 cumsum 을 진행하여 인덱스를 뽑아 냅니다.
pca = PCA()
pca.fit(X_train)
cumsum = np.cumsum(pca.explained_variance_ratio_)
d = np.argmax(cumsum >= 0.95) + 1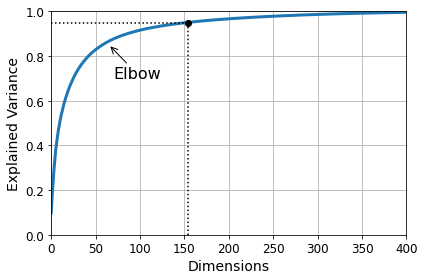
이제 이렇게 찾은 값을 적용시켜 줍니다.
pca = PCA(n_components=0.95)
X_reduced = pca.fit_transform(X_train)
np.sum(pca.explained_variance_ratio_)
=> 0.9504334914295707- 추가적인 PCA
1) PCA
# auto, randomized, full
rnd_pca = PCA(n_components=154, svd_solver=" ", random_state=42)
X_reduced = rnd_pca.fit_transform(X_train)2) 점진적 PCA
from sklearn.decomposition import IncrementalPCA
n_batches = 100
inc_pca = IncrementalPCA(n_components=154)
for X_batch in np.array_split(X_train, n_batches):
inc_pca.partial_fit(X_batch)
X_reduced = inc_pca.transform(X_train)3) 커널 PCA - 스위스 롤과 같은 데이터셋 잘 축소
lin_pca = KernelPCA(n_components=2, kernel="linear", fit_inverse_transform=True)
rbf_pca = KernelPCA(n_components=2, kernel="rbf", gamma=0.0433, fit_inverse_transform=True)
sig_pca = KernelPCA(n_components=2, kernel="sigmoid", gamma=0.001, coef0=1, fit_inverse_transform=True)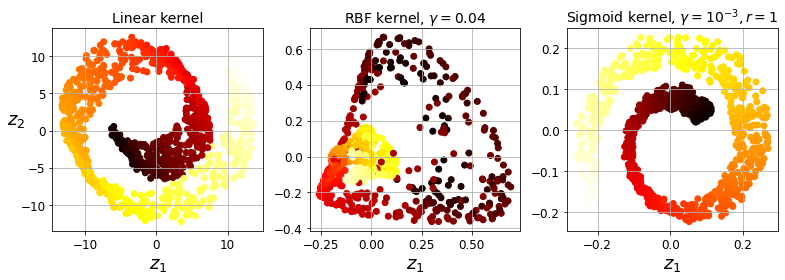
- 하이퍼 파라미터 튜닝
from sklearn.model_selection import GridSearchCV
from sklearn.linear_model import LogisticRegression
from sklearn.pipeline import Pipeline
clf = Pipeline([
("kpca", KernelPCA(n_components=2)),
("log_reg", LogisticRegression(solver="lbfgs"))
])
param_grid = [{
"kpca__gamma": np.linspace(0.03, 0.05, 10),
"kpca__kernel": ["rbf", "sigmoid"]
}]
grid_search = GridSearchCV(clf, param_grid, cv=3)
grid_search.fit(X, y)
print(grid_search.best_params_)PCA 압축 후 이점
예를 들어 MNIST데이터셋에 분산 95% 유지 PCA를 적용하면, 특성의 개수를 784->150 정도로 줄일 수 있습니다. 이렇게 축소시킨 데이터셋은 분산을 잘 유지할 뿐 아니라, 모델 알고리즘의 속도를 크게 높일 수 있습니다.
고려대학교 응용수학 - 1. Five importance Factorization를 참고하시면 좋습니다.
데이터 압축의 한 예시

Wallis의 "dressed to kill" 광고 이미지들중 하나인데, 이 600x367 이미지를 SVD로 압축해보자.
truncated SVD를 이용하여 근사행렬 A'을 구한 후 이를 다시 이미지로 표시해 보면 아래와 같다.
1) 100개의 singular value로 근사 (t = 100)

2) 50개의 singular value로 근사 (t = 50)

3) 20개의 singular value로 근사 (t = 20)

기존의 이미지는 367x600 = 220x200의 메모리가 필요했지만, singular value 20개로 줄여
-> 600x20 (U) + 20x367 (Σ) + 20x367 (V) = 19,360 으로
압축률 = (19,360 / 220,220) x 100 = 8.8% 임을 알 수 있다.
화질을 보면 좋은 압축 방법은 아님을 알 수 있지만 truncated SVD를 통한 데이터 근사가 원래의 데이터 핵심을 잘 잡아내고 있음을 알 수 있다!
4. LLE : locally linear embedding
LLE는 지역 선형 임베딩으로 mainfold learning의 한 비선형 차원 축소 입니다.
이 알고리즘은 이전 PCA와 달리 투영에 의존하지 않습니다.
LLE
1) 이웃 찾기 : n neighbors
먼저 가장 가까운 이웃에 얼마나 선형적으로 연관되어 있는 지 측정
2) 이웃에 대한 선형 함수로 재구성
국부적인 관계가 가장 잘 보존되는 훈련 셋의 저차원 표현 찾기=> 이러한 방법을 통해 꼬인 매니폴드를 펼치는 데 잘 작동합니다.
우선 이웃을 몇 개로 할 지 정해줍니다.
그 후 아래와 같이 각 데이터에 대해 이웃과의 제곱 거리가 최소가 되는 w값을 찾습니다.
(여기서 목적함수와 minimize식을 이용하여 라그랑주 승수법을 통해 w를 구합니다.)

이렇게 가중치 행렬을 구하고 이번에는 매핑후에도 관계를 잘 보존하기 위해 원본 데이터 xi가 subspace에 매핑된 이미지를 z라고 했을 때, 이 z를 찾는 과정을 수행합니다.
(이번에는 w가 변하는 값이 아닙니다! w 고정)

하지만 이 알고리즘은 계산 복잡도가 O(dm^2)으로 인해 대량의 데이터셋에는 적용하기 어렵습니다.
코드는 아래와 같습니다.
from sklearn.manifold import LocallyLinearEmbedding
lle = LocallyLinearEmbedding(n_components=2, n_neighbors=10)
X_reduced = lle.fit_transform(X)