Stochastic Gradient Descent (SGD)
1. SGD Classifier
- 판다스 데이터프레임을 생성한다.
import pandas as pd
fish = pd.read_csv('https://bit.ly/fish_csv_data')- Species 열을 제외한 나머지 5개를 입력 데이터로 사용한다.
fish_input = fish[['Weight','Length','Diagonal','Height','Width']].to_numpy()
fish_target = fish['Species'].to_numpy()- 데이터를 훈련 세트와 테스트 세트로 나눈다.
from sklearn.model_selection import train_test_split
train_input, test_input, train_target, test_target = train_test_split(
fish_input, fish_target, random_state=42)- 훈련 세트와 테스트 세트의 특성을 표준화 전처리한다.
from sklearn.preprocessing import StandardScaler
ss = StandardScaler()
ss.fit(train_input)
train_scaled = ss.transform(train_input)
test_scaled = ss.transform(test_input)scikit-learn에서 확률적 경사 하강법을 제공하는 대표적인 분류용 class는 SGDClassifier이다.
SGDClassifier의 객체를 만들 때, 2개의 매개변수를 지정합니다.
loss = 손실 함수의 종류 지정
max_iter = 수행할 에포크 횟수 지정
from sklearn.linear_model import SGDClassifier
sc = SGDClassifier(loss='log', max_iter=10, random_state=42)
sc.fit(train_scaled, train_target)
print(sc.score(train_scaled, train_target))
# 0.773109243697479
print(sc.score(test_scaled, test_target))
# 0.775출력된 훈련 세트와 테스트 세트 정확도가 낮다.
확률적 경사 하강법은 점진적 학습이 가능하다.
훈련한 모델 sc를 추가로 더 훈련해 보자.
모델을 이어서 훈련할 때는 partial_fit() method를 사용한다.
이 method는 fit() method와 사용법이 같지만, 호출할 때마다 1 에포크씩 이어서 훈련할 수 있다.
sc.partial_fit(train_scaled, train_target)
print(sc.score(train_scaled, train_target))
# 0.8151260504201681
print(sc.score(test_scaled, test_target))
# 0.85아직 점수가 낮긴 하지만, 에포크를 한 번 더 실행하니 정확도가 향상되었다.
이 모델을 여러 에포크에서 더 훈련해 볼 필요가 있는데, 얼마나 훈련을 더 해야할 지에 대한 기준이 필요하다.
2. Epoch and Overfitting/Underfitting
확률적 경사 하강법을 사용한 모델은 에포크 횟수에 따라 underfitting이나 overfitting이 될 수 있다.
적은 에포크 횟수 동안에 훈련한 모델은 훈련 세트를 덜 학습하여 underfitting된 모델일 가능성이 높다.
반대로, 많은 에포크 횟수 동안에 훈련한 모델은 훈련 세트에 너무 잘 맞아, 테스트 세트에는 오히려 점수가 나쁜 overfitting된 모델일 가능성이 높다.
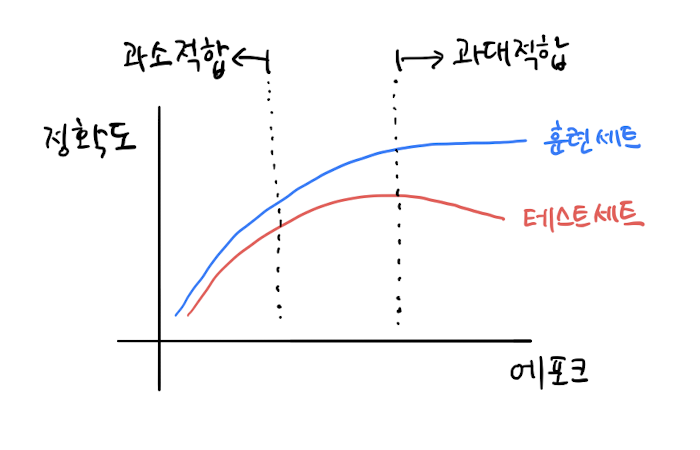
훈련 세트 점수는 에포크가 진행될수록 꾸준히 증가하지만, 테스트 세트 점수는 어느 순간 감소한다. 이 지점이 이 모델이 overfitting되기 시작하는 곳이다.
여기서는 partial_fit() method만 사용할 건데, 그럴려면 훈련 세트에 있는 전체 클래스의 레이블을 partial_fit() method에 전달해 주어야 한다.
import numpy as np
sc = SGDClassifier(loss='log', random_state=42)
train_score = []
test_score = []
classes = np.unique(train_target)
# -----
# 300번의 에포크 진행
for _ in range(0, 300):
sc.partial_fit(train_scaled, train_target, classes=classes)
train_score.append(sc.score(train_scaled, train_target))
test_score.append(sc.score(test_scaled, test_target))
# -----
import matplotlib.pyplot as plt
plt.plot(train_score)
plt.plot(test_score)
plt.xlabel('epoch')
plt.ylabel('accuracy')
plt.show()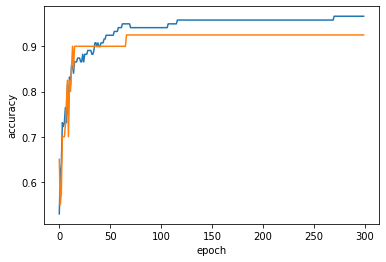
백 번째 에포크 이후에는 훈련 세트와 테스트 세트의 점수가 조금씩 벌어지고 있다. 또한, 에포크 초기에는 과소적합되어 훈련 세트와 테스트 세트의 점수가 낮다.
에포크를 100으로 줄이고 다시 훈련을 해보자.
sc = SGDClassifier(loss='log', max_iter=100, tol=None, random_state=42)
sc.fit(train_scaled, train_target)
print(sc.score(train_scaled, train_target))
# 0.957983193277311
print(sc.score(test_scaled, test_target))
# 0.925SGDClassifier는 일정 에포크 동안 성능이 향상되지 않으면 더 훈련하지 않고 자동으로 멈춘다.
tol 매개변수는 향상될 최솟값을 지정한다.
SGDClassifier의 loss 매개변수에 대해 잠시 살펴보면, loss 매개변수의 기본값은 hinge이다.
Hinge loss는 support vector machine(SVM)이라 불리는 손실 함수이다.
sc = SGDClassifier(loss='hinge', max_iter=100, tol=None, random_state=42)
sc.fit(train_scaled, train_target)
print(sc.score(train_scaled, train_target))
# 0.9495798319327731
print(sc.score(test_scaled, test_target))
# 0.925Feature Engineering and Regularization
1. Data Preparation
지난 시간에는 하나의 특성을 사용해 선형 회귀(linear regression)을 훈련시켰다.
이번 시간에는 여러 개의 특성을 사용할 건데, 이처럼 여러 개의 특성을 사용한 선형 회귀를 다중 회귀(multiple regression) 라고 부른다.
이 예제에서는 농어의 길이뿐만 아니라 농어의 깊이와 두께도 함께 사용한다.
또한 3개의 특성을 각각 제곱하여 추가하고 각 특성을 서로 곱해서 또 다른 특성을 만든다.
이렇게 기존의 특성을 사용해 새로운 특성을 뽑아내는 작업을 특성 공학(feature engineering) 이라고 부른다.
import pandas as pd
df = pd.read_csv('https://bit.ly/perch_csv_data')
perch_full = df.to_numpy()
print(perch_full)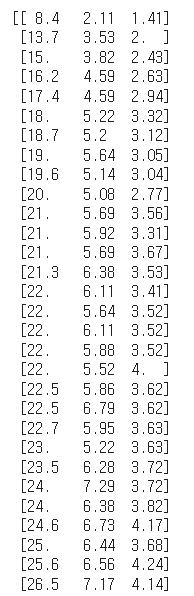
(일부분만 크롭)
perch_full과 perch_weight를 훈련 세트와 테스트 세트로 나누자.
# target data
import numpy as np
perch_weight = np.array(
[5.9, 32.0, 40.0, 51.5, 70.0, 100.0, 78.0, 80.0, 85.0, 85.0,
110.0, 115.0, 125.0, 130.0, 120.0, 120.0, 130.0, 135.0, 110.0,
130.0, 150.0, 145.0, 150.0, 170.0, 225.0, 145.0, 188.0, 180.0,
197.0, 218.0, 300.0, 260.0, 265.0, 250.0, 250.0, 300.0, 320.0,
514.0, 556.0, 840.0, 685.0, 700.0, 700.0, 690.0, 900.0, 650.0,
820.0, 850.0, 900.0, 1015.0, 820.0, 1100.0, 1000.0, 1100.0,
1000.0, 1000.0]
)
# -----
from sklearn.model_selection import train_test_split
train_input, test_input, train_target, test_target =
train_test_split(perch_full, perch_weight, random_state=42)2. Transformer of Scikit-learn
scikit-learn은 특성을 만들거나 전처리하기 위한 다양한 클래스를 제공한다. 이런 클래스를 변환기(transformer)라고 부른다.
2개의 특성으로, 2와 3으로 이루어진 샘플 하나를 적용하자.
fit() method는 새롭게 만들 특성 조합을 찾고, transform() method는 실제로 데이터를 변환한다.
from sklearn.preprocessing import PolynomialFeatures
poly = PolynomialFeatures()
poly.fit([[2, 3]])
print(poly.transform([[2, 3]]))
# [[1. 2. 3. 4. 6. 9.]]2개의 특성(원소)을 가진 샘플 [2,3]이 6개의 특성을 가진 샘플 [[1. 2. 3. 4. 6. 9.]]로 바뀌었다.
poly = PolynomialFeatures(include_bias=False)
poly.fit([[2, 3]])
print(poly.transform([[2, 3]]))
# [[2. 3. 4. 6. 9.]]절편을 위한 항이 제거되고 특성의 제곱과 특성끼리 곱한 항만 추가되었다.
poly = PolynomialFeatures(include_bias=False)
poly.fit(train_input)
train_poly = poly.transform(train_input)
print(train_poly.shape) # (42, 9)PolynomialFeatures class는 get_feature_names() method를 호출하면 9개의 특성이 각각 어떤 입력의 조합으로 만들어졌는지 알려 준다.
poly.get_feature_names_out()
# array(['x0', 'x1', 'x2', 'x0^2', 'x0 x1', 'x0 x2', 'x1^2', 'x1 x2'
# ,'x2^2'], dtype=object)
test_poly = poly.transform(test_input)'x0'은 첫 번째 특성을 의미하고, 'x0^2'는 첫 번째 특성의 제곱, 'x0 x1'은 첫 번째 특성과 두 번째 특성의 곱을 나타내는 식이다.
3. Training Multiple Regression Model
from sklearn.linear_model import LinearRegression
lr = LinearRegression()
lr.fit(train_poly, train_target)
print(lr.score(train_poly, train_target))
# 0.9903183436982124
print(lr.score(test_poly, test_target))
# 0.9714559911594134테스트 세트에 대한 점수는 높아지지 않았지만, 농어의 길이만 사용했을 때 있던 underfitting 문제는 더 이상 나타나지 않는다.
특성을 더 추가하여, 5제곱 항까지 특성을 만들어 출력해보자.
poly = PolynomialFeatures(degree=5, include_bias=False)
poly.fit(train_input)
train_poly = poly.transform(train_input)
test_poly = poly.transform(test_input)
print(train_poly.shape) # (42, 55)train_poly 배열의 열의 개수가 특성의 개수이다.
이 데이터를 사용해 선형 회귀 모델을 다시 훈련하자.
lr.fit(train_poly, train_target)
print(lr.score(train_poly, train_target))
# 0.9999999999991097
print(lr.score(test_poly, test_target))
# -144.40579242684848훈련 세트에 대한 점수는 거의 완벽하지만, 테스트 세트에 대한 점수는 아주 큰 음수이다.
특성의 개수를 크게 늘리면 선형 모델은 훈련 세트에 대해 거의 완벽하게 학습할 수 있다.
하지만 이런 모델은 너무 overfitting되므로 테스트 세트에서는 점수가 크게 떨어진다.
4. Regularization
Regularization은 모델이 훈련 세트에 overfitting되지 않도록 만드는 것이다.
선형 회귀 모델의 경우, 특성에 곱해지는 계수(또는 기울기)의 크기를 작게 만든다.
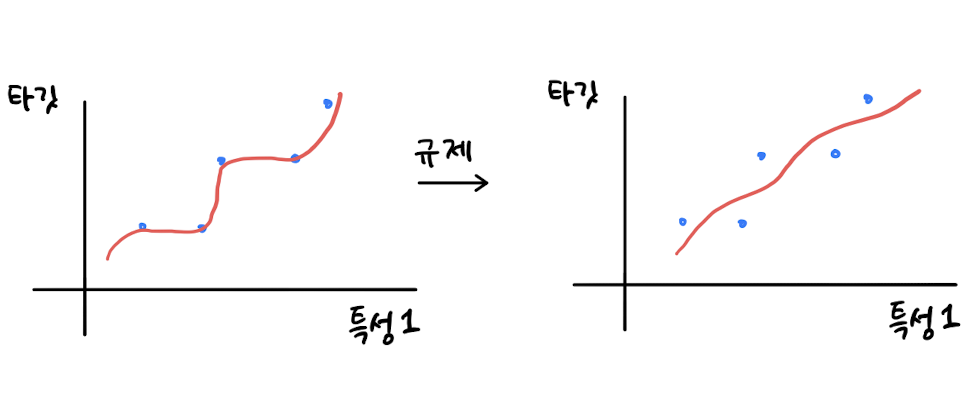
앞서 55개의 특성으로 훈련한 선형 회귀 모델의 계수를 규제하여 훈련 세트의 점수를 낮추고, 대신 테스트 세트의 점수를 높여 보자.
그 전에, 특성의 스케일을 정규화하기 위해 scikit-learn에서 제공하는 StandardScaler class를 사용하여 표준점수로 변환하자.
from sklearn.preprocessing import StandardScaler
ss = StandardScaler()
ss.fit(train_poly)
train_scaled = ss.transform(train_poly)
test_scaled = ss.transform(test_poly)선형 회귀 모델에 regularization을 추가한 모델을 Ridge와 Lasso 라고 부른다.
Ridge는 계수를 제곱한 값을 기준으로 규제를 적용하고,
Lasso는 계수의 절대값을 기준으로 규제를 적용한다.
두 알고리즘 모두 계수의 크기를 줄이지만, Lasso는 아예 0으로 만들 수도 있다.
Ridge (L2 Regularization)
train_scaled 데이터로 Ridge 모델을 훈련해 보자.
from sklearn.linear_model import Ridge
ridge = Ridge()
ridge.fit(train_scaled, train_target)
print(ridge.score(train_scaled, train_target))
# 0.9896101671037343
print(ridge.score(test_scaled, test_target))
# 0.9790693977615397Ridge와 Lasso 모델을 사용할 때, regularization의 양을 임의로 조절할 수 있다. 모델 객체를 만들 때, alpha 매개변수로 regularization의 강도를 조절한다.
적절한 alpha 값을 찾는 한 가지 방법은 alpha 값에 대한 R^2 값의 그래프를 그려 보는 것이다.
alpha 값을 바꿀 때마다 score() method의 결과를 저장할 리스트를 만든다.
import matplotlib.pyplot as plt
train_score = []
test_score = []
# alpha 값을 0.001에서 100까지 10배씩 늘려가며
# Ridge 회귀 모델을 훈련한 다음,
# 훈련 세트와 테스트 세트의 점수를 파이썬 리스트에 저장
alpha_list = [0.001, 0.01, 0.1, 1, 10, 100]
for alpha in alpha_list:
# 릿지 모델을 만듦
ridge = Ridge(alpha=alpha)
# 릿지 모델을 훈련
ridge.fit(train_scaled, train_target)
# 훈련 점수와 테스트 점수를 저장
train_score.append(ridge.score(train_scaled, train_target))
test_score.append(ridge.score(test_scaled, test_target))
plt.plot(np.log10(alpha_list), train_score)
plt.plot(np.log10(alpha_list), test_score)
plt.xlabel('alpha')
plt.ylabel('R^2')
plt.show()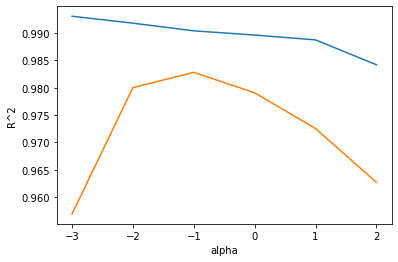
위는 훈련 세트 그래프, 아래는 테스트 세트 그래프이다.
적절한 alpha 값은 두 그래프가 가장 가깝고 테스트 세트의 점수가 가장 높은 -1, 즉 0.1이다.
alpha 값을 0.1로 하여 최종 모델을 훈련하자.
ridge = Ridge(alpha=0.1)
ridge.fit(train_scaled, train_target)
print(ridge.score(train_scaled, train_target))
# 0.9903815817570366
print(ridge.score(test_scaled, test_target))
# 0.9827976465386926Lasso (L1 Regularization)
from sklearn.linear_model import Lasso
lasso = Lasso()
lasso.fit(train_scaled, train_target)
print(lasso.score(train_scaled, train_target))
# 0.989789897208096
print(lasso.score(test_scaled, test_target))
# 0.9800593698421883
train_score = []
test_score = []
alpha_list = [0.001, 0.01, 0.1, 1, 10, 100]
for alpha in alpha_list:
# 라쏘 모델을 만듦
lasso = Lasso(alpha=alpha, max_iter=10000)
# 라쏘 모델을 훈련
lasso.fit(train_scaled, train_target)
# 훈련 점수와 테스트 점수를 저장
train_score.append(lasso.score(train_scaled, train_target))
test_score.append(lasso.score(test_scaled, test_target))
plt.plot(np.log10(alpha_list), train_score)
plt.plot(np.log10(alpha_list), test_score)
plt.xlabel('alpha')
plt.ylabel('R^2')
plt.show()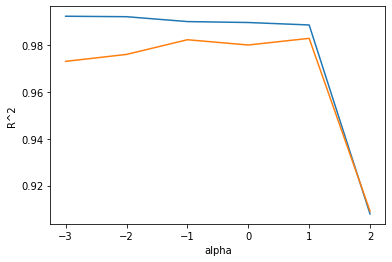
Lasso 모델에서 최적의 alpha 값은 1, 즉 10이다.
이 값으로 다시 모델을 훈련하자.
lasso = Lasso(alpha=10)
lasso.fit(train_scaled, train_target)
print(lasso.score(train_scaled, train_target))
# 0.9888067471131867
print(lasso.score(test_scaled, test_target))
# 0.9824470598706695Lasso 모델은 계수 값을 아예 0으로 만들 수 있다.
coef_ 속성을 통해 계수가 0인 것을 확인해보자.
print(np.sum(lasso.coef_ == 0)) # 40
