분류 (classification) - 몇 개의 클래스 중 하나를 분류
회귀 (regression) - 임의의 어떤 숫자를 예측
K-NN의 한계
저번 실습에서는 도미와 농어의 데이터를 가지고 분류 실습을 진행했다.
이번에는 농어의 데이터만 가지고 농어의 길이만으로 무게를 예측해보자!
1. 산점도 그려보기
import matplotlib.pyplot as plt
plt.scatter(perch_length, perch_weight)
plt.xlabel('length')
plt.ylabel('weight')
plt.show()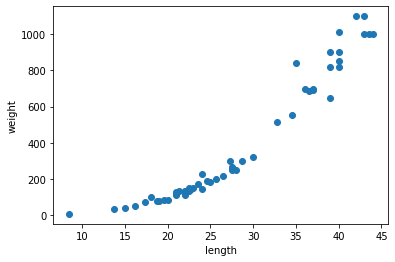
길이가 늘어남에 따라 무게가 늘어나는 것을 볼 수 있다.
2. 훈련/테스트 세트 분리
from sklearn.model_selection import train_test_split
# 훈련 세트와 테스트 세트로 나눕니다.
train_input, test_input, train_target, test_target = train_test_split(
perch_length, perch_weight, random_state=42)Scikit-learn에 사용할 훈련 세트는 2차원 배열이어야 한다.
지난 시간까지는 2개의 특성을 사용했기 때문에 자연스럽게 열이 2개인 2차원 배열을 사용했다.
이번 예제에서는 길이 특성 1개만 사용하기 때문에 수동으로 2차원 배열을 만들어야 한다. 넘파이 배열은 크기를 바꿀 수 있는 reshape() method를 사용하면 된다.
#reshape 예제
test_array = test_array.reshape(2, 2) # (4,) -> (2,2)
# 실제 코드
# -1 : 나머지 원소 개수로 모두 채우라는 뜻
train_input = train_input.reshape(-1, 1)
test_input = test_input.reshape(-1, 1)
print(train_input.shape, test_input.shape)
3. K-NN 훈련 (K=3)
from sklearn.neighbors import KNeighborsRegressor
knr = KNeighborsRegressor(n_neighbors=3) # 모델을 만들고
knr.fit(train_input, train_target) # 모델을 훈련
print(knr.predict([[50]])) # 길이가 50인 농어의 무게 예측
# [1033.33333333]길이가 50인 농어의 무게를 1033.33333333으로 예측했다.
하지만 실제 이 농어의 무게는 훨씬 더 많이 나간다.
무엇이 잘못되었는지 보기 위해 산점도를 다시 그려보자.
4. 산점도로 문제 상황 분석
import matplotlib.pyplot as plt
# 50cm 농어의 이웃을 구한다.
distances, indexes = knr.kneighbors([[50]])
# 훈련 세트의 산점도를 그린다.
plt.scatter(train_input, train_target)
# 훈련 세트 중에서 이웃 샘플만 다시 그린다.
plt.scatter(train_input[indexes], train_target[indexes], marker='D')
# 50cm 농어 데이터
plt.scatter(50, 1033, marker='^')
plt.xlabel('length')
plt.ylabel('weight')
plt.show()
print(np.mean(train_target[indexes])) # 1033.3333333333333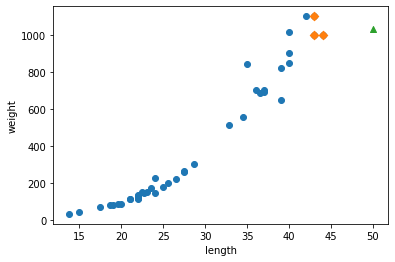
50cm 농어에 가장 가까운 이웃은 45cm 근방이기 때문에 K-NN은 이 샘플들의 평균을 계산한다.
그렇기 때문에 100cm 농어를 input으로 주어도 1033.3333333333333이 나올 것이다.
이런 식이라면, 농어의 길이가 늘어나도 농어의 무게 예측값은 늘어나지 않는다.
이럴 때, 선형 회귀(linear regression) 알고리즘을 사용하자.
Linear regression
선형 회귀 (linear regression)는 널리 사용되는 대표적인 회귀 알고리즘이다.
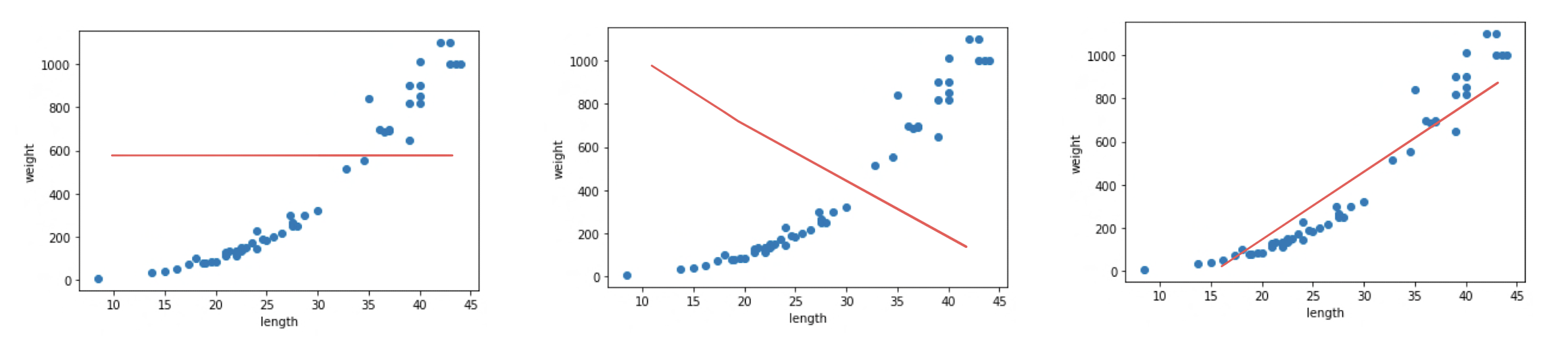
Scikit-learn의 sklearn.linear_model 패키지 아래에 LinearRegression 클래스로 선형 회귀 알고리즘을 구현되어있다.
이 클래스의 객체를 만들어 훈련을 하자.
from sklearn.linear_model import LinearRegression
lr = LinearRegression() # 객체 생성
# 선형 회귀 모델 훈련
lr.fit(train_input, train_target)
print(lr.predict([[50]])) # [1241.83860323]K-NN 회귀와 다르게 선형 회귀는 50cm 농어의 무게를 더 높게 예측했다.

선형 회귀가 학습한 직선은 (농어 무게) = a * (농어 길이) + b이고, LinearRegression 클래스는 데이터에 가장 잘 맞는 a와 b를 찾았다고 볼 수 있다.
LinearRegression 클래스가 찾은 a와 b는 lr 객체의 coef와 intercept 속성에 저장되어 있다.
print(lr.coef_, lr.intercept_)
# [39.01714496] -709.0186449535477coef와 intercept는 머신러닝 알고리즘을 통해 찾은 값이라는 의미로 모델 파라미터(model parameter) 라고 부른다.
대부분 사용하는 많은 머신러닝 알고리즘의 훈련 과정은 최적의 모델 파라미터를 찾는 것과 같다. 이를 모델 기반 학습이라고 부른다.
하지만, 앞서 실습한 K-NN에는 모델 파라미터가 없다.
훈련 세트를 저장하는 것이 훈련의 전부였다. 이를 사례 기반 학습이라고 부른다.
이제 산점도에 선형 회귀 직선을 그려보자.
# 훈련 세트의 산점도
plt.scatter(train_input, train_target)
# 15에서 50까지 1차 방정식 그래프를 그린다
plt.plot([15, 50], [15*lr.coef_+lr.intercept_, 50*lr.coef_+lr.intercept_])
# 50cm 농어 데이터
plt.scatter(50, 1241.8, marker='^')
plt.xlabel('length')
plt.ylabel('weight')
plt.show()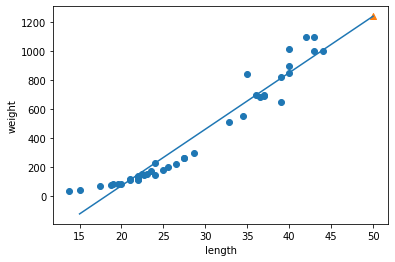
이 직선이 선형 회귀 알고리즘을 통해 찾은 최적의 직선이다.
길이가 50cm인 농어의 무게는 직선의 연장선에 존재한다.
이번에는 훈련 세트와 테스트 세트에 대한 점수를 확인해 보자.
여기서 점수는 이전 분류에서의 점수와는 조금 다르다.
분류의 경우는 테스트 세트에 있는 샘플을 정확하게 분류한 개수의 비율로 정확도라고 불렀다.
하지만, 회귀에서는 정확한 숫자를 맞힌다는 것은 거의 불가능하다.
회귀의 경우에는 조금 다른 값으로 평가하는데, 이 점수를 결정계수(coefficient of determination)라고 부른다. 또는 간단히 R^2라고도 부른다.
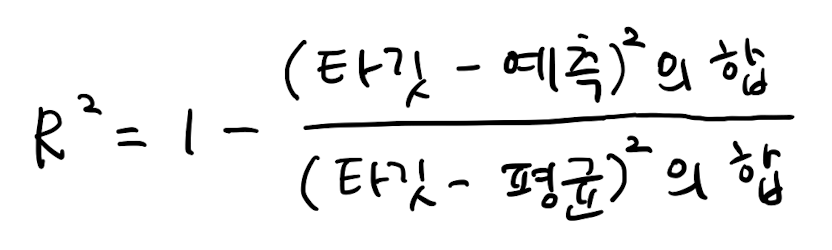
훈련 세트와 테스트 세트의 R^2를 계산해보자.
print(lr.score(train_input, train_target)) # 훈련 세트
# 0.939846333997604
print(lr.score(test_input, test_target)) # 테스트 세트
0.8247503123313558훈련 세트와 테스트 세트의 점수가 조금 차이가 나는 것을 볼 수 있다.
훈련 세트에서 점수가 굉장히 좋았는데 테스트 세트에서는 점수가 굉장히 나쁘다면, 모델이 훈련 세트에 과대적합(overfitting)되었다고 말한다.
반대로, 훈련 세트보다 테스트 세트의 점수가 높거나 두 점수가 모두 낮은 경우는 모델이 훈련 세트에 과소적합(underfitting)되었다고 말한다.
즉, 모델이 너무 단순하여 훈련 세트에 적절히 훈련되지 않은 경우를 말한다.
Polynomial Regression
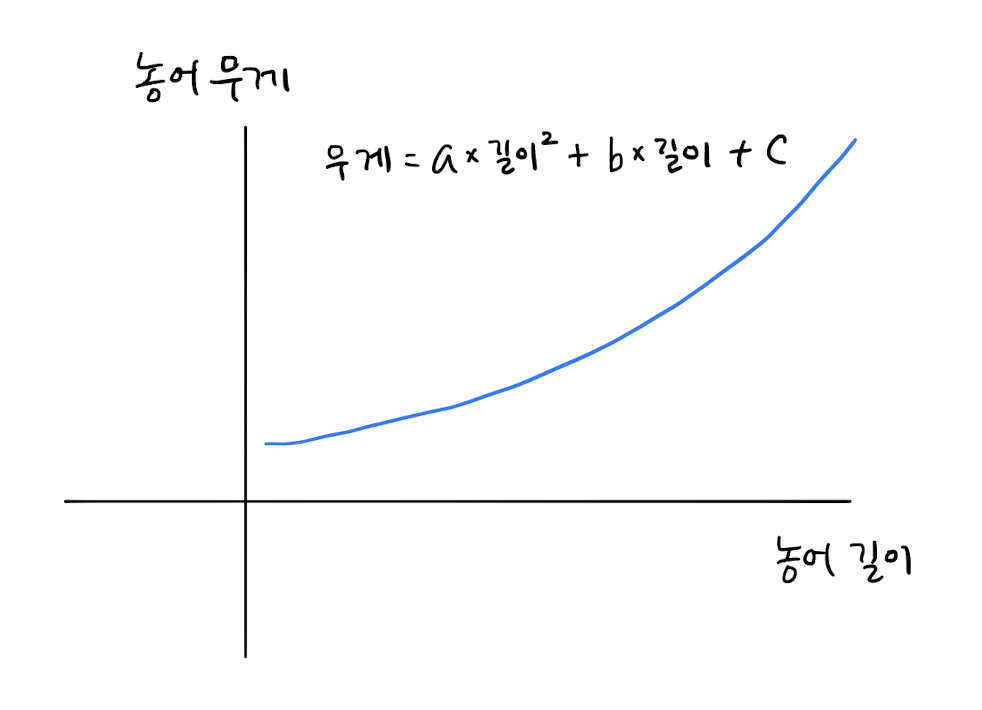
위와 같은 2차 방정식의 그래프를 그리려면 길이를 제곱한 항이 훈련 세트에 추가되어야 한다.
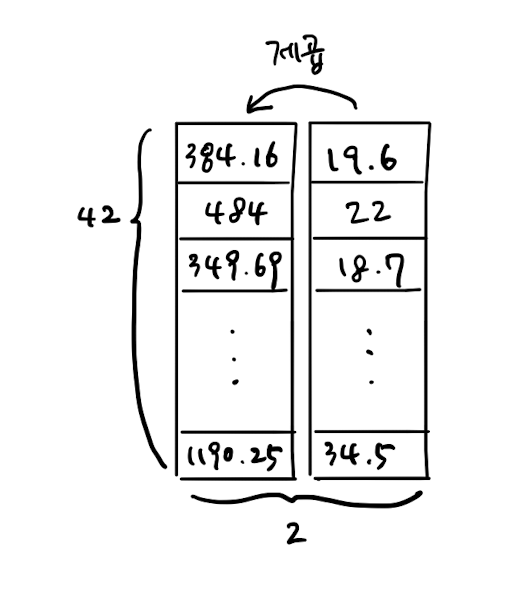
위 사진처럼 농어의 길이를 제곱해서 원래 데이터 앞에 붙여 보자.
column_stack() 함수를 사용하면 간단하게 구현할 수 있다.
train_poly = np.column_stack((train_input ** 2, train_input))
test_poly = np.column_stack((test_input ** 2, test_input))원래 특성인 길이를 제곱하여 왼쪽 열에 추가했기 때문에 훈련 세트와 테스트 세트 모두 열이 2개로 늘어났다.
이제 train_poly를 사용해 선형 회귀 모델을 다시 훈련한 다음 50cm짜리 농어에 대해 무게를 예측해 보자.
lr = LinearRegression()
lr.fit(train_poly, train_target)
print(lr.predict([[50**2, 50]]))
# [1573.98423528]이전에 예측한 1241.83860323보다 높은 값을 예측했다.
모델이 훈련한 계수와 상수항을 살펴보자.
print(lr.coef_, lr.intercept_)
# [ 1.01433211 -21.55792498] 116.0502107827827즉, 모델이 학습한 그래프는 아래와 같다.
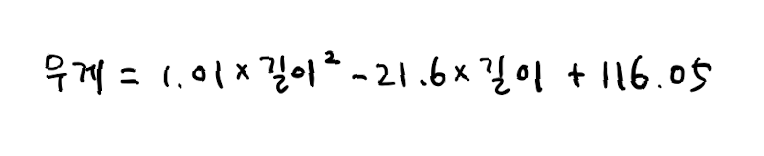
이런 방정식을 다항식이라고 부르며 다항식을 사용한 선형 회귀를 다항 회귀(polynomial regression) 라고 부른다.
다항 회귀 그래프의 산점도를 그리면 아래와 같다.
# 구간별 직선을 그리기 위해 15에서 49까지 정수 배열을 만든다
point = np.arange(15, 50)
# 훈련 세트의 산점도를 그린다
plt.scatter(train_input, train_target)
# 15에서 49까지 2차 방정식 그래프를 그린다.
plt.plot(point, 1.01*point**2 - 21.6*point + 116.05)
# 50cm 농어 데이터
plt.scatter([50], [1574], marker='^')
plt.xlabel('length')
plt.ylabel('weight')
plt.show()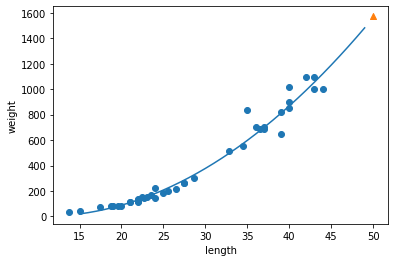
훈련 세트와 테스트 세트의 R^2를 평가해보자.
print(lr.score(train_poly, train_target))
# 0.9706807451768623
0.9775935108325122
print(lr.score(test_poly, test_target))
# 0.9775935108325122기존 0.939846333997604,0.8247503123313558과 비교했을 때 점수가 크게 높아진 것을 볼 수 있다.
Logistic Regression
이름은 회귀지만, 실제로는 분류 모델이다.
1. Data preparation
판다스(pandas) 는 유명한 데이터 분석 라이브러리입니다.
데이터프레임(dataframe)은 판다스의 핵심 데이터 구조입니다.
넘파이 배열과 비슷하게 다차원 배열을 다룰 수 있지만 훨씬 더 많은 기능을 제공합니다.
판다스를 이용해 데이터를 인터넷에서 내려받아 데이터프레임에 저장하고, 넘파이 배열로 변환해 모델을 훈련해봅시다.
판다스 데이터프레임을 만들기 위해 많이 사용하는 파일은 CSV 파일이다. CSV 파일은 아래 그림처럼 콤마로 나누어져 있는 텍스트 파일입니다.
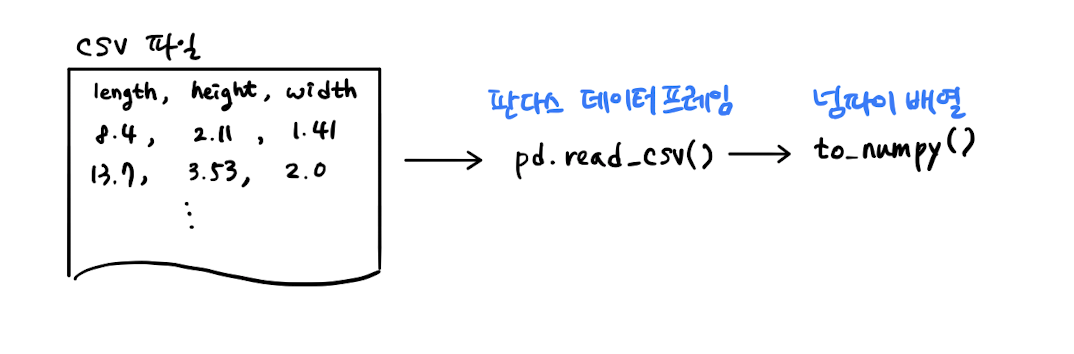
import pandas as pd
fish = pd.read_csv('https://bit.ly/fish_csv_data')
fish.head() # 처음 5개를 출력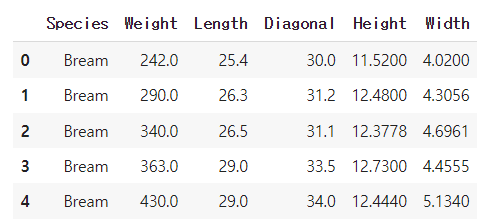
판다스의 unique 함수를 이용하여 Species 열에서 고유한 값들을 추출할 수 있다.
print(pd.unique(fish['Species']))
# ['Bream' 'Roach' 'Whitefish' 'Parkki' 'Perch' 'Pike' 'Smelt']이 데이터프레임에서 Species 열을 타깃으로 만들고, 나머지 5개 열은 입력 데이터로 사용하자.
데이터프레임에서 열을 선택하는 방법은 데이터프레임에서 원하는 열을 리스트로 나열하면 된다.
fish_input = fish[['Weight','Length','Diagonal','Height','Width']].to_numpy()
이제 동일한 방법으로 타깃 데이터를 만들자.
fish_target = fish['Species'].to_numpy()이제 훈련 세트와 테스트 세트를 나누자.
그리고 Scikit-learn의 StandardScaler 클래스를 사용해 훈련 세트와 테스트 세트를 표준화 전처리하자.
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
train_input, test_input, train_target, test_target = train_test_split(
fish_input, fish_target, random_state=42)
ss = StandardScaler()
ss.fit(train_input)
train_scaled = ss.transform(train_input)
test_scaled = ss.transform(test_input)2. Probability Prediction of K-NN Classifier
from sklearn.neighbors import KNeighborsClassifier
kn = KNeighborsClassifier(n_neighbors=3)
kn.fit(train_scaled, train_target)
print(kn.score(train_scaled, train_target))
# 0.8907563025210085
print(kn.score(test_scaled, test_target))
# 0.85앞서 fish 데이터프레임에서 7개의 생선이 있었다. 타깃 데이터를 만들 때 fish['Species']를 사용해 만들었기 때문에 훈련 세트와 테스트 세트의 타깃 데이터에도 7개의 생선 종류가 들어가 있다.
이렇게 타깃 데이터에 2개 이상의 클래스가 포함된 문제를 다중 분류(multi-class classification) 라고 부른다.
이진 분류를 사용했을 때는 양성 클래스와 음성 클래스를 각각 1과 0으로 지정하여 타깃 데이터를 만들었다.
다중 분류에서도 타깃값을 숫자로 바꾸어 입력할 수 있지만, Scikit-learn에서는 편리하게도 문자열로 된 타깃 값을 그대로 사용할 수 있습니다.
이때 주의할 점은 타깃값을 그대로 Scikit-learn 모델에 전달하면 순서가 자동으로 알파벳 순으로 매겨지므로, pd.unique(fish['Species'])로 출력했던 순서와 다르다
KNeighborsClassifier에서 정렬된 타깃값은 classes_ 속성에 저장되어 있습니다.
print(kn.classes_)
# ['Bream' 'Parkki' 'Perch' 'Pike' 'Roach' 'Smelt' 'Whitefish']
# -> 알파벳 순으로 정렬됨테스트 세트에 있는 5개 샘플의 타깃값을 예측해보자.
print(kn.predict(test_scaled[:5]))
# ['Perch' 'Smelt' 'Pike' 'Perch' 'Perch'] Scikit-learn의 분류 모델은 predict_proba() method로 클래스별 확률값을 반환한다.
테스트 세트에 있는 처음 5개의 샘플에 대한 확률을 출력해 보자.
넘파이 round() 함수는 기본으로 소수점 첫째 자리에서 반올림 하는데, decimals 매개변수로 유지할 소수점 아래 자릿수를 지정할 수 있습니다.
import numpy as np
proba = kn.predict_proba(test_scaled[:5])
print(np.round(proba, decimals=4)) # 소수점 네 번째 자리까지 표기, 다섯 번째 자리에서 반올림.
# [[0. 0. 1. 0. 0. 0. 0. ]
# [0. 0. 0. 0. 0. 1. 0. ]
# [0. 0. 0. 1. 0. 0. 0. ]
# [0. 0. 0.6667 0. 0.3333 0. 0. ]
# [0. 0. 0.6667 0. 0.3333 0. 0. ]]출력 순서는 classes_ 속성의 순서와 동일하다.
['Bream' 'Parkki' 'Perch' 'Pike' 'Roach' 'Smelt' 'Whitefish']

이 모델이 계산한 확률이 가장 가까운 이웃의 비율과 맞는지 4번째 샘플을 사용하여 확인해보자.
distances, indexes = kn.kneighbors(test_scaled[3:4])
print(train_target[indexes])
# [['Roach' 'Perch' 'Perch']]이 샘플의 이웃은 다섯 번째 클래스인 'Roach'가 1개이고 세 번째 클래스인 'Perch'가 2개이다.
따라서, 다섯 번째 클래스에 대한 확률은 1/3 = 0.3333이고, 세 번째 클래스에 대한 확률은 2/3 = 0.6667이 된다.
앞서 출력한 네 번째 샘플의 클래스 확률과 같다.
3. Logistic Regression
로지스틱 회귀(logistic regression)는 이름은 회귀이지만 분류 모델이다. 이 알고리즘은 선형 회귀와 동일하게 선형 방정식을 학습한다.
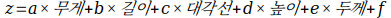
여기에서 a, b, c, d, e는 가중치 혹은 계수이다. 특성은 늘어났지만 다중 회귀를 위한 선형 방정식과 같습니다. z는 어떤 값도 가능하다.
하지만 확률이 되려면 0 ~ 1(또는 0~100%) 사이 값이 되어야 합니다. z가 아주 큰 음수일 때 0이 되고, z가 아주 큰 양수일 때 1이 되도록 바꾸려면 시그모이드 함수(sigmoid function) = 로지스틱 함수(logistic function) 를 사용하면 됩니다.

왼쪽의 식이 시그모이드 함수이다.
- 선형 방정식의 출력의 음수를 사용해
- 자연 상수 e를 거듭제곱하고 1을 더한 값의
- 역수를 취한다.
시그모이드 함수의 그래프는 오른쪽과 같다.
z가 어떤 값이 되더라도 𝜙는 절대로 0 ~ 1 사이의 범위를 벗어날 수 없다.
그렇다면 0 ~ 1 사이 값을 0 ~ 100%까지 확률로 해석할 수 있다.
Perform Binary Classification with Logistic Regression
훈련을 하기 전 간단한 이진 분류를 수행해보자.
이진 분류일 경우, 시그모이드 함수의 출력이 0.5보다 크면 양성 클래스, 0.5보다 작으면 음성 클래스로 판단한다.
도미와 빙어 2개를 사용해서 이진 분류를 수행해 보자.
불리언 인덱싱(boolean indexing)을 사용하여 넘파이 배열에서 True, False 값을 전달해 행을 선택한다.
다음과 같이 'A'에서 'E'까지 5개의 원소로 이루어진 배열이 있을 때, 'A'와 'C'만 골라내려면 첫 번째와 세 번째 원소만 True이고 나머지 원소는 모두 False인 배열을 전달하면 된다.
char_arr = np.array(['A', 'B', 'C', 'D', 'E'])
print(char_arr[[True, False, True, False, False]])
# ['A' 'C']이와 같은 방식을 사용해, 훈련 세트에서 도미(Bream)와 빙어(Smelt)의 행만 골라내보자.
비교 연산자를 사용하면 도미와 빙어의 행을 모두 True로 만들 수 있다.
예를 들어, 도미인 행을 골라내려면 train_target=='Bream'과 같이 쓴다. 이 비교식은 train_target 배열에서 'Bream'인 것은 True이고 그 외는 모두 False인 배열을 반환한다.
도미와 빙어에 대한 비교 결과를 비트 OR 연산자(|)를 사용해 합치면 도미와 빙어에 대한 행만 골라낼 수 있다.
bream_smelt_indexes = (train_target == 'Bream') | (train_target == 'Smelt')
train_bream_smelt = train_scaled[bream_smelt_indexes]
target_bream_smelt = train_target[bream_smelt_indexes]bream_semlt_indexes 배열은 도미와 빙어일 경우 True이고 그 외는 모두 False 값이 들어가 있다.
따라서, 이 배열을 사용해 train_scaled와 train_target 배열에 불리언 인덱싱을 적용하면 손쉽게 도미와 빙어 데이터만 골라낼 수 있다.
이제 이 데이터로 로지스틱 회귀 모델을 훈련해 보자.
LogisticRegression 클래스는 선형 모델이므로, sklearn.linear_model 패키지 아래 있다.
from sklearn.linear_model import LogisticRegression
lr = LogisticRegression()
lr.fit(train_bream_smelt, target_bream_smelt)KNeighborsClassifier와 마찬가지로 예측 확률은 predict_proba() method에서 제공한다.
train_bream_smelt에서 처음 5개 샘플의 예측확률을 출력해보자.
print(lr.predict_proba(train_bream_smelt[:5]))
# [[0.99759855 0.00240145]
# [0.02735183 0.97264817]
# [0.99486072 0.00513928]
# [0.98584202 0.01415798]
# [0.99767269 0.00232731]]샘플마다 2개의 확률이 출력되었다. 첫 번째 열이 음성 클래스(0)에 대한 확률이고 두 번째 확률이 양성 클래스(1)에 대한 확률이다.
K-NN 분류기에서 봤듯이 Scikit-learn은 타깃값을 알파벳순으로 정렬하여 사용한다. 그러므로, Smelt(빙어)가 양성 클래스가 된다.
로지스틱 회귀가 학습한 계수를 확인해보자.
print(lr.coef_, lr.intercept_)
# [[-0.4037798 -0.57620209 -0.66280298 -1.01290277 -0.73168947]] [-2.16155132]이를 방정식으로 표현하면 아래와 같다.
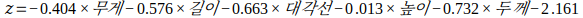
LogisticRegression 클래스는 decision_function() method로 z 값을 출력할 수 있다.
train_bream_smelt의 처음 5개 샘플의 z 값을 출력해 보자.
decisions = lr.decision_function(train_bream_smelt[:5])
print(decisions)
# [-6.02927744 3.57123907 -5.26568906 -4.24321775 -6.0607117 ]이 값을 시그노이드 함수에 통과시키면 확률을 얻을 수 있다.
파이썬의 Scipy 라이브러리에도 시그모이드 함수인 expit()가 있다.
np.exp() 함수를 사용해 분수 계산을 하는 것보다 훨씬 편리하고 안전합니다.
expit() 함수를 이용해 decisions 배열의 값을 확률로 변환해 봅시다.
from scipy.special import expit
print(expit(decisions))
# [0.00240145 0.97264817 0.00513928 0.01415798 0.00232731]출력된 값을 보면 predict_proba() method 출력의 두 번째 열의 값과 동일하다.
즉, decision_function() method는 양성 클래스에 대한 z 값을 반환한다.
Perform Multiple Classification with Logistic Regression
이번에는 7개의 생선을 분류하는 다중 분류 문제를 수행해보자.
LogisticRegression 클래스는 기본적으로 반복적인 알고리즘을 사용한다. max_iter 매개변수에서 반복 횟수를 지정하며, 기본값은 100입니다.
여기에 준비한 데이터셋을 사용해 모델을 훈련하면 반복 횟수가 부족하다는 경고가 발생한다. 충분하게 훈련시키기 위해 반복 횟수를 1,000으로 늘려주자.
또 LogisticRegression은 기본적으로 릿지 회귀와 같이 계수의 제곱을 규제한다. 이런 규제를 L2 규제라고도 부른다.
LogisticRegression에서 규제를 제어하는 매개변수는 C이다. C가 작을수록 규제가 커지며, C의 기본값은 1이다. 여기에서는 규제를 조금 완화하기 위해 20으로 늘리자.
이제 LogisticRegression 클래스로 다중 분류 모델을 훈련해보자.
7개의 생선 데이터가 모두 들어 있는 train_scaled와 train_target을 사용한다.
# C 완화, 반복 횟수 늘리기
lr = LogisticRegression(C=20, max_iter=1000)
lr.fit(train_scaled, train_target) # 훈련
print(lr.score(train_scaled, train_target))
# 0.9327731092436975
print(lr.score(test_scaled, test_target))
# 0.925
# 처음 5개 샘플에 대한 예측 확률
proba = lr.predict_proba(test_scaled[:5])
print(np.round(proba, decimals=3))
# [[0. 0.014 0.841 0. 0.136 0.007 0.003]
# [0. 0.003 0.044 0. 0.007 0.946 0. ]
# [0. 0. 0.034 0.935 0.015 0.016 0. ]
# [0.011 0.034 0.306 0.007 0.567 0. 0.076]
# [0. 0. 0.904 0.002 0.089 0.002 0.001]]첫 번째 샘플을 보면 세 번째 열의 확률이 84.1%로 가장 높다. 세 번째 열이 농어(Perch)에 대한 확률인지 classes_ 속성에서 클래스 정보를 확인해 보자.
print(lr.classes_)
# ['Bream' 'Parkki' 'Perch' 'Pike' 'Roach' 'Smelt' 'Whitefish']세 번째 열이 농어에 대한 확률이 맞았음을 확인할 수 있다.
print(lr.coef_.shape, lr.intercept_.shape)
# (7, 5) (7,)이 데이터는 5개의 특성을 사용하므로 coef 배열의 열은 5개이다.
그런데 행이 7이고 intercept도 7개가 있다.
이는 이진 분류에서 보았던 z를 7개나 계산한다는 의미이다.
즉, 다중 분류는 클래스마다 z 값을 하나씩 계산한다.
가장 높은 z 값을 출력하는 클래스가 예측 클래스가 된다.
이진 분류에서 확률은 시그모이드 함수를 사용해 z를 0과 1 사이의 값으로 변환했다.
다중 분류는 이와 달리, 소프트맥스(softmax) 함수를 사용해 7개의 z 값을 확률로 변환합니다.
소프트맥스 계산 방식은 다음과 같다.
- 7개의 z 값의 이름을 z1에서 z7이라고 붙인다.
- z1 ~ z7까지 값을 사용해 지수 함수 e^{z1} ~ e^{z7}을 계산해 모두 더한다. => e_sum
(e_sum = e^{z1} + e^{z2} + .. + e^{z7})- e^{z1} ~ e^{z7}을 각각 e_sum으로 나누어 준다.
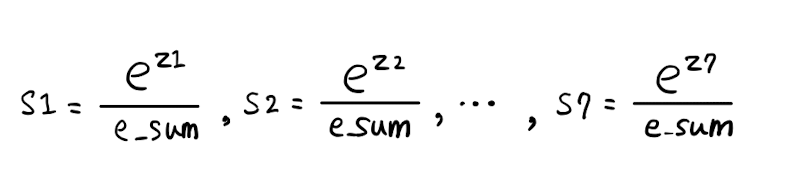
s1에서 s7까지 모두 더하면 분자와 분모가 같아지므로 1이 된다.
# 테스트 세트의 처음 5개 샘플에 대한 z1 ~ z7의 값
decision = lr.decision_function(test_scaled[:5])
print(np.round(decision, decimals=2))
#[[ -6.5 1.03 5.16 -2.73 3.34 0.33 -0.63]
# [-10.86 1.93 4.77 -2.4 2.98 7.84 -4.26]
# [ -4.34 -6.23 3.17 6.49 2.36 2.42 -3.87]
# [ -0.68 0.45 2.65 -1.19 3.26 -5.75 1.26]
# [ -6.4 -1.99 5.82 -0.11 3.5 -0.11 -0.71]]
from scipy.special import softmax
proba = softmax(decision, axis=1)
print(np.round(proba, decimals=3))
# [[0. 0.014 0.841 0. 0.136 0.007 0.003]
# [0. 0.003 0.044 0. 0.007 0.946 0. ]
# [0. 0. 0.034 0.935 0.015 0.016 0. ]
# [0.011 0.034 0.306 0.007 0.567 0. 0.076]
# [0. 0. 0.904 0.002 0.089 0.002 0.001]]앞서 구한 decision 배열을 softmax() 함수에 전달했다.
softmax()의 axis 매개변수는 소프트맥스를 계산할 축을 지정한다. 여기에서는 axis=1로 지정하여 각 행, 즉 각 샘플에 대해 소프트맥스를 계산합니다.
만약 axis 매개변수를 지정하지 않으면 배열 전체에 대해 소프트맥스를 계산합니다.
출력 결과가 앞서 구한 proba 배열과 비교하면 결과가 정확히 일치하는 것을 볼 수 있다.

