1. ML(Machine Learning)

1-0) ML 이란?

① 어떠한 작업 T에 대해서
② 경험E와 함께
③ 성능P를 향상시킨다.
즉, 데이터와 출력값을 주어서 컴퓨터가 스스로 프로그램을 만드는 것

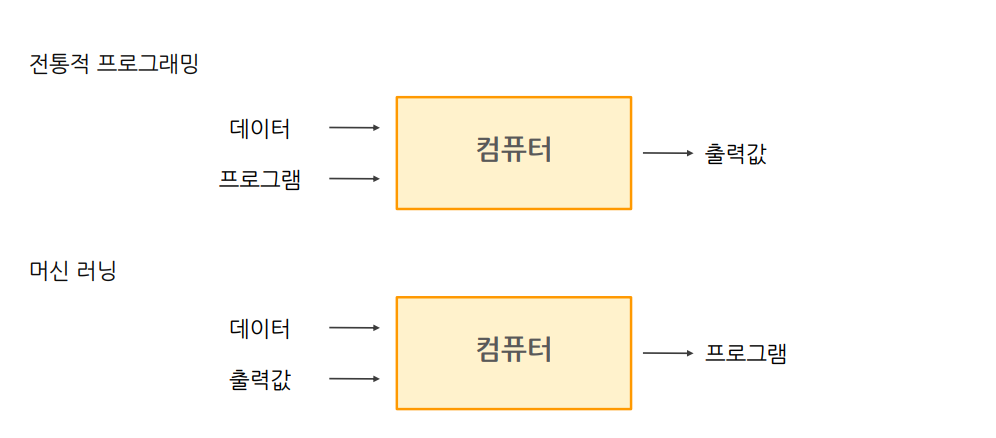
1-1) 학습의 종류

1-1-0) 지도학습

• 학습데이터와 레이블(원하는 출력)을 세트로 제공해서 컴퓨터가 최대한 맞는 답을 찾도록 하는 것.

1-1-0) 비지도학습

• 학습데이터만이 제공되면 원하는 출력이 없다. 알아서 잘 합리적으로 분리하도록 기대.

1-1-0) 강화학습

• 일련의 행동에 따른 보상을 하도록 함..!

1-2) 머신러닝 라이플 사이클

1. Project Plan Setup
2. Collection and Labelling Data
3. Model Exploration
4. Refinement of Model
5. Test and Evaluate
6. Deployment of Model

2. Linear Regression

• 정의 : 선형회귀는 종속 변수와 하나 이상의 독립 변수 간의 관계를 모델링하는 통계적 방법
  👉 독립변수의 값을 통해 종속변수의 값을 예측하기 위함.

2-0) Linear Regression 가정

① 선형성 : 종속변수와 독립변수의 관계는 선형적이어야 함.
② 독립성 : 관측값들은 서로 독립적이어야 함.
③ 등분산성 : 오류의 분산이 일정해야 함
④ 정규성 : 오류가 정규 분포를 따릅니다.

2-1) OLS(Ordinary Least Square)

: 관측값과 예측값의 차이(잔차)의 제곱합을 최소화하는 매개변수 $m$과 $b$ 를 추정하는 방법

$Cost(m,b) = \sum(y_i - (mx_i +b))^2$

2-2) 모델 평가지표

① 평균 절대 오차(MAE)

$\text{MAE} = \frac{1}{n} \sum_{i=1}^{n} \left|y_i -\hat{y}_i \right|$

예측 값과 실제 값과 얼마나 차이나는지 절대값으로 계산해 평균화한 지표

②
$\text{MSE} = \frac{1}{n} \sum_{i=1}^{n} \left(y_i - \hat{y}_i\right)^2$

실제 값과 예측 값 간의 차이의 제곱을 평균낸 값

2-3) Neighbor Classifier

import numpy as np
class NearestNeighbor:
	def __init__(self):
    	pass
    
    def train(self, images, labels):
    	self.images = images
        self.labels = labels
        
	def predict(self, test_image):
    	min_dist = sys.maxint
        for i in range(self.images.shape[0]):
        	dist = np.sum(np.abs(self.images[i,:] - test_image))
            if dist < min_dist:
            	min_dist = dist
                min_index = i
    return self.labels[min_index]

3. 필요한 수학적 수식

3-0) Sigmoid

$\sigma(x) = \frac{1}{1 + e^{-x}}$

3-1) Softmax

$\text{Softmax}(x_i) = \frac{e^{x_i}}{\sum_{j=1}^{n} e^{x_j}}$

3-2) Cross_Entropy

$H(y, \hat{y}) = - \sum_{i=1}^{n} y_i \log(\hat{y}_i)$

3-3) Gradient_Descent

$\theta := \theta - \eta \nabla_\theta J(\theta)$