목차 (Table of Contents)

1. 0. 사전지식
   1.1 KL Divergence
   1.2 Bayes Rule

2. 1. What is a generative model?

3. 2. Why we use generative models?

   • Statistical Generative Models
     • 개념 정리
     • Priors (사전 지식)
     • 모델 학습
     • 요약

4. 3. How to train generative models?

   • 1) 최대우도 학습(MLE)
   • 2) 잠재변수(latent 변수) 모델
   • 3) 마진Likelihood(주변우도)와 부분 관측 데이터
   • 4) 근사 기법 1: Naive Monte Carlo
   • 5) 근사 기법 2: 중요도 샘플링
   • 6) 세 번째 시도: 변분 추론(Variational Inference)
   • 7) 변분 추론(Variational Inference) 개념과 ELBO 도입

5. [5] 변분 추론(Variational Inference) 개념과 ELBO 도입

6. [6] ELBO 최적화를 통한 (\theta)와 (\phi)의 동시 학습

7. [7] ELBO의 해석

   • (8) 정리

8. 1. Partially Observed Data의 로그-우도( Log-Likelihood ) 계산의 어려움

9. 2. Jensen's Inequality ( concave 함수에 대한 부등식 )

10. 3. ELBO( Evidence Lower Bound )의 정의 및 해석

11. 4. Auto-Encoding Variational Bayes (VAE) 구조 개요

12. 5. VAE의 학습 목표: ELBO 최적화

13. 6. VAE의 동작 과정

14. 7. VAE 훈련 목표(직관적 해석)

15. 종합 요약

---

0. 사전지식

KL Divergence

• $KL(q\|p)$ 는 “$q$ 분포에서 뽑힌 표본을 $p$로 설명하려고 할 때 드는 정보 손실”로 해석할 수 있습니다.
• $KL(p\|q)$ 는 “$p$ 분포에서 뽑힌 표본을 $q$로 설명하려고 할 때 드는 정보 손실”에 가깝습니다.
• 두 형태는 일반적으로 값이 다르고, ‘누구를 기준으로 삼고, 누구를 타겟으로 보는가?’에 따라 의미와 ‘페널티(손실을 주는 방식)’가 달라집니다.

1. 기본 정의 복습

두 분포 $p(x)$와 $q(x)$가 있을 때,

이 두 값은 일반적으로 같지 않습니다.
(즉, $KL(q\|p) \;\neq\; KL(p\|q)$)

2. 해석에서의 차이

2.1 $KL(q\|p)$: “$q$에서 본 표본을 $p$로 부호화할 때의 정보 손실”

• 중심이 되는 분포: $q$

  • 내가 ‘현재 쓰고 싶은(혹은 근사하고 싶은)’ 분포가 $q$일 때,
  • 실제(타겟) 분포는 $p$라고 했을 때,
  • “$q$가 만들어내는 샘플들”을 “$p$가 얼마나 잘 맞출 수 있나?”를 보는 관점.

• 즉, 평균적으로 $q(x)$가 큰 부분(자주 발생시키는 지점)에서, $p(x)$가 너무 작으면 $\log\frac{q(x)}{p(x)}$ 항이 커져서 $KL(q\|p)$가 커집니다.

• $KL(q\|p)$를 최소화하려면,

  • $q$가 많이 분포(mass)를 두는 지점에서 $p$가 그걸 놓치지 않게끔(즉, $p$가 너무 0에 가깝지 않도록) 해야 합니다.

• 흔히 말하는 “모드 커버링(mode covering)” 성향이 있습니다.

  • $q$가 커버하는(자주 등장하는) 영역을 $p$가 놓치면 큰 손실이 되기 때문입니다.

2.2 $KL(p\|q)$: “$p$에서 본 표본을 $q$로 부호화할 때의 정보 손실”

• 중심이 되는 분포: $p$

  • 내가 ‘참 분포(ground truth)’라고 생각하는 것이 $p$라면,
  • 이 표본(샘플)들을 $q$로 설명하려고 할 때 정보 손실이 얼마나 되는가?

• 평균적으로 $p(x)$가 큰 부분(자주 등장하는 실제 데이터 영역)에서, $q(x)$가 너무 작으면 $\log\frac{p(x)}{q(x)}$가 커져 $KL(p\|q)$가 커집니다.

• $KL(p\|q)$를 최소화하려면,

  • $p$가 자주 발생시키는 영역을 $q$가 확실히 커버해야 합니다.

• 오히려 $p(x)\approx0$인 영역(실제 데이터가 거의 등장하지 않는 곳)에서 $q(x)$가 약간 커도 큰 페널티가 아닙니다.

• 따라서 $KL(p\|q)$를 최소화하는 쪽은 “모드 추구(mode seeking)” 혹은 “대표 모드에 집중”하는 경향을 띱니다.

3. 예시로 보는 차이

3.1 단순 예시: 양봉 vs. 벌통

• $p$: 실제 벌들이 자주 모이는 위치 분포
• $q$: 우리가 추정하거나 인위적으로 배치한 벌통(벌집) 위치 분포

$KL(q\|p)$:

• “우리가 벌통을 여기저기 놨는데, 실제 벌들이 과연 거기에 오는가?”
• 벌통이 놓인 지점($q$가 큰 곳)에 실제 벌($p$)이 거의 없다면 헛벌통 → 손실이 큼.

$KL(p\|q)$:

• “실제로 벌이 많이 모이는 장소에 벌통이 없으면, 그만큼 손실이 크다.”
• $p$가 큰 지점을 $q$가 놓치면 페널티가 큼.

즉, “샘플이 어디서 오느냐”에 따라 페널티가 달라지는 것을 볼 수 있습니다.

4. 요약

$KL(q\|p)$

• $q$가 자주 등장하는 지역을 $p$가 놓치면 큰 페널티.
• 모드 커버링(mode covering) 경향.
• 변분추론에서 자주 $KL(q\|p)$ 형태를 사용.
  • “$q$”(근사분포)가 표현하고자 하는 지점을 “$p$”(목표분포)가 놓치면 손실이 커짐.

$KL(p\|q)$

• $p$에서 자주 등장하는 지역을 $q$가 놓치면 큰 페널티.
• 모드 추구(mode seeking) 성향.
• MLE(Maximum Likelihood Estimation) 같은 관점에서 “실제 데이터 분포($p$)를 모델($q$)로 피팅”할 때 사용.
• GAN 등에서 $JSD(p\|q)$나 다른 지표를 사용하는 것도 모드 소실(mode collapse) 문제와 연관됨.

결국, $KL(q\|p)$ vs. $KL(p\|q)$는

• “샘플이 $q$에서 오고, 그것을 $p$로 설명하려 하는가?”
• “샘플이 $p$에서 오고, 그것을 $q$로 설명하려 하는가?”
  라는 시점 차이로 인해 페널티가 달라지고, 최적화 결과도 달라지게 됩니다.

Bayes' Rule

베이즈 정리는 관측된 데이터(증거, evidence)를 바탕으로 불확실한 사건(또는 파라미터)에 대한 사후 확률(posterior probability)을 업데이트하는 방법을 제시합니다.

1. 공식 (Bayes’ Rule)

• 사전확률(Prior): 실제 데이터를 관측하기 이전에, 파라미터(또는 가설) $\theta$에 대해 갖고 있던 신념(확률).
• 가능도(Likelihood): 관측 데이터 $x$가, 특정 파라미터(가설) $\theta$로부터 얼마나 잘 설명되는지(발생 가능한가)를 나타내는 함수.
• 증거도(Evidence): 실제로 관측된 데이터 $x$ 그 자체의 확률. (일종의 정규화 상수 역할)
• 사후확률(Posterior): 데이터를 관측한 이후, 파라미터(가설) $\theta$에 대한 업데이트된 신념(확률).

2. 예시: 의료 검진 테스트

가령, 어떤 질병(A)이 있을 확률(유병률)이 1%라고 하자.
이제 검진 테스트를 해봤는데, 결과가 "양성"이 나왔다고 했을 때, 실제로 병에 걸렸을 확률이 얼마인지 알고 싶습니다.

1. 사전확률(Prior)

   • 질병 A를 가지고 있을 확률: 0.01
   • 질병 A가 없을 확률: 0.99

2. 가능도(Likelihood)

   • 테스트가 정확도가 95%라고 가정해 봅시다. (양성일 때 95% 확률로 양성으로 진단, 음성일 때 95% 확률로 음성으로 진단)
   • 질병 A가 있을 때(test ‘양성’일 확률): 0.95
   • 질병 A가 없을 때(test ‘양성’일 확률): 0.05

3. 증거도(Evidence)

   • 실제 ‘양성’ 결과가 나올 전체 확률:
     $p(\text{양성}) = p(\text{양성}\mid A)\,p(A) + p(\text{양성}\mid \neg A)\,p(\neg A) = 0.95 \times 0.01 + 0.05 \times 0.99 = 0.0095 + 0.0495 = 0.059.$

4. 사후확률(Posterior)

   • 베이즈 정리에 따라,
     $p(A \mid \text{양성}) = \frac{p(\text{양성}\mid A)\,p(A)}{p(\text{양성})} = \frac{0.95 \times 0.01}{0.059} = \frac{0.0095}{0.059} \approx 0.161.$
   • 즉, 검진에서 양성이 나왔어도, 실제로 질병에 걸렸을 확률은 약 16.1%라는 의미입니다.

3. 요약

• 베이즈 정리란, 관측 데이터를 통해 기존의 ‘사전확률(prior)’을 업데이트하여 ‘사후확률(posterior)’을 얻는 과정입니다.
• 수식:
  $p(\theta \mid x) = \frac{p(x \mid \theta)\, p(\theta)}{p(x)}.$
• 예시(질병 검사): 유병률이 낮은 병을 검사했을 때, 양성 판정이 나와도 실제 발병 확률은 낮을 수 있음을 잘 보여줍니다.

1. What is a generative model?

The Era of Generative AI

Transformer & Diffusion

• Language: ChatGPT
• Vision: Stable Diffusion
• Multimodal: GPT4

GAN의 출현과 생성 모델의 발전 흐름 (Ver. 2021)

GAN모델이 세상을 거진 10년이나 지배하였습니다. 그후에 21년에 유명한 NeRF 논문이 나왔고 OpenAI에서 DALLE(VQ-VAE)를 출시하면서 이 세상에 없는 이미지 아보카토 이미지들을 생성해내기 시작하였습니다.

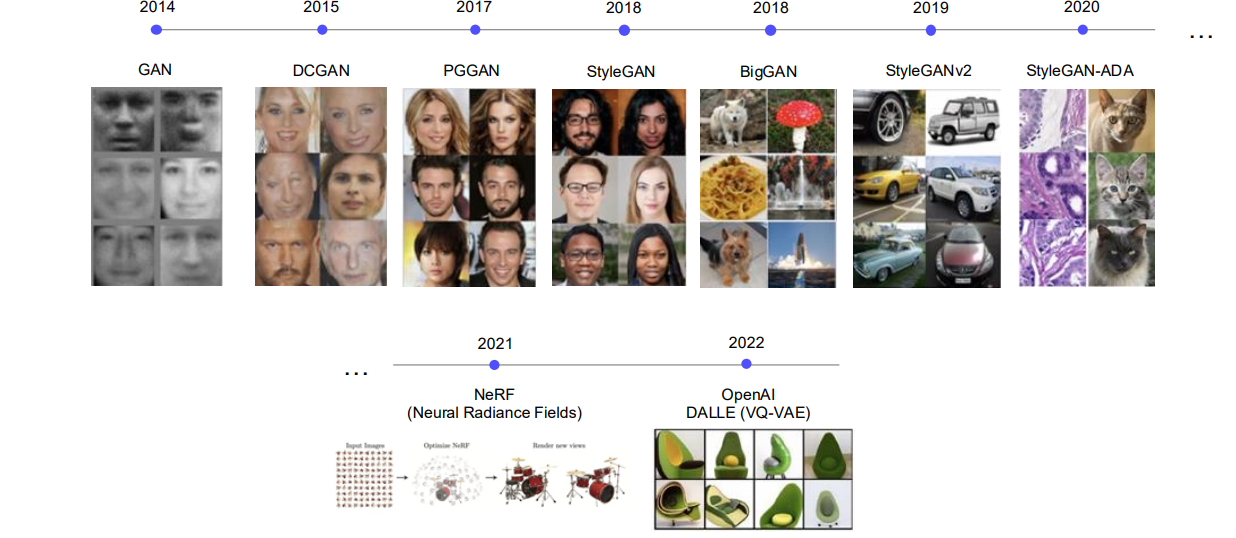
Diffusion based Generative Model의 출현 (Ver. 2022)

이미지의 퀄리티가 높아지고 video로도 생성이 가능해졌습니다.

그렇다면 Generative modeling 이라는 것이 무엇인가?

분포도를 예상하여 이미지를 생성하는 것입니다.

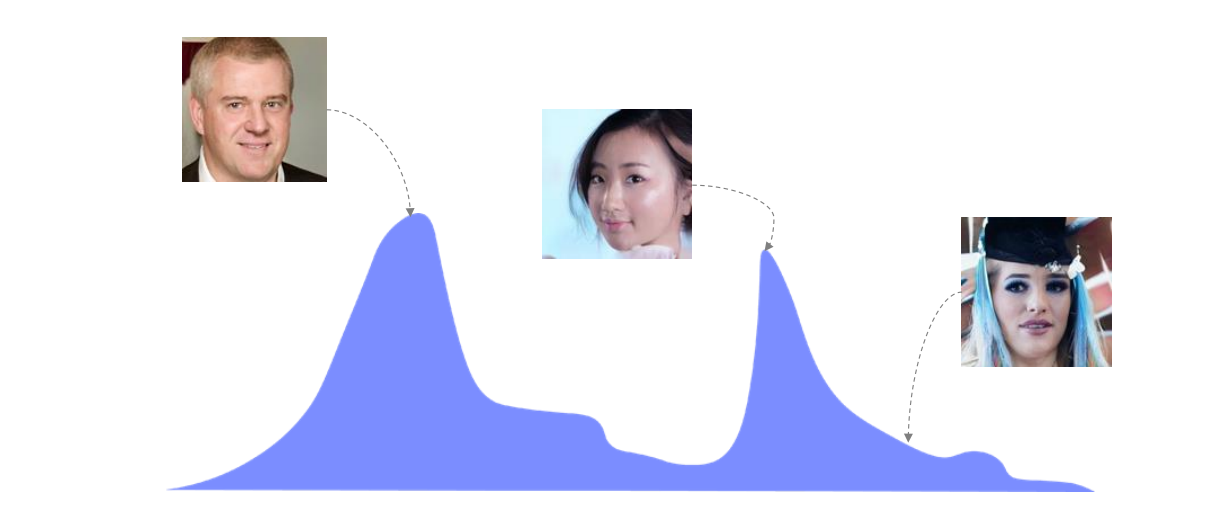
2. Why we use generative models?

Statistical Generative Models

1. 개념 정리

• Statistical generative model은 학습된 확률분포 $p(x)$를 통해 데이터를 생성할 수 있는 모델을 말합니다.
• 데이터를 관측(샘플)하고, 사전지식(예: 분포의 형태 가정, 손실함수, 최적화 알고리즘 등)을 활용하여 모델을 학습합니다.
• 학습이 끝나면, $p(x)$에서 샘플링함으로써 새로운 데이터를 만들어낼 수 있으므로 ‘생성 모델(generative model)’이라고 부릅니다.
  

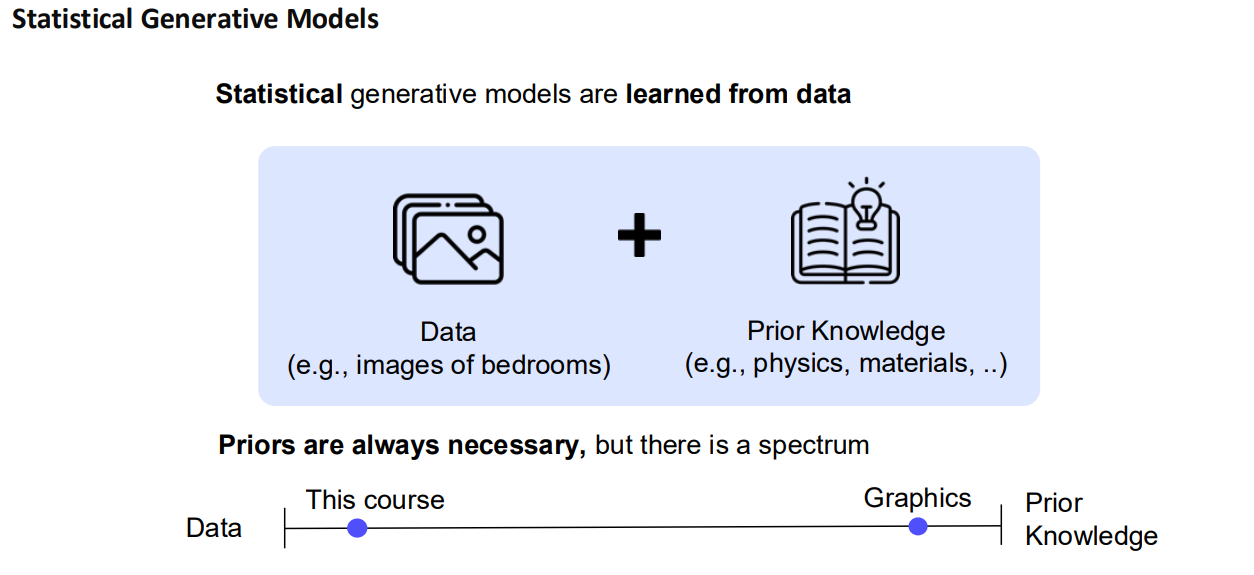
2. Priors (사전 지식)

• 사전 분포(prior)는 반드시 필요하지만, 그 정도는 모델마다 다릅니다.
  • 예: 간단한 가우시안 분포 가정, 복잡한 신경망 기반 분포 등
  • 얼마나 강한 사전지식을 사용하느냐에 따라 모델의 유연성과 복잡도가 달라집니다.

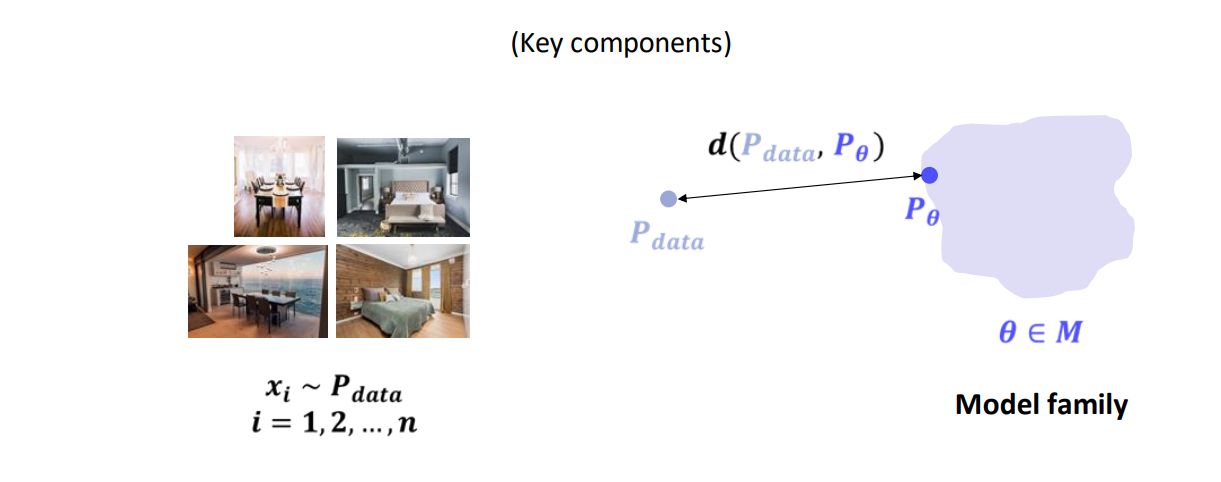
3. 모델 학습: $\min_\theta \, \text{Distance}(P_\theta, P_{\text{data}})$

• 우리가 가지고 있는 데이터 분포를 $P_{\text{data}}$라고 할 때,
• 어떤 모델 패밀리 $\theta$ (예: $\theta$가 가우시안의 평균·분산이 될 수도 있고, 복잡한 뉴럴넷 파라미터가 될 수도 있음)가 주어지면,
• “$P_{\text{data}}$와 가장 가깝도록” $\theta$를 학습하는 과정을 거칩니다.
  • 이는 흔히 “$\text{Distance}(P_\theta, P_{\text{data}})$를 최소화”하는 문제로 표현할 수 있습니다.
  • 구체적인 거리(혹은 손실함수)로 KL 다이버전스, MSE, 크로스 엔트로피 등 다양한 방식이 쓰일 수 있습니다.

4. 요약

1. Statistical Generative Model: 확률분포 $p(x)$를 학습해서 새로운 데이터를 생성할 수 있는 모델
2. 데이터 & 사전지식:
   • 데이터: 예) 침실 이미지를 모은 샘플들
   • 사전지식: 분포 형태, 손실함수, 최적화 알고리즘 등
3. 학습 목표: 모델 분포 $P_\theta$가 실제 데이터 분포 $P_{\text{data}}$와 ‘가장 가깝도록’ $\theta$를 찾아내는 것
4. 생성: 학습된 분포 $p_\theta(x)$에서 샘플링해 새로운 이미지를 생성할 수 있음

Note:

• “Distance” 또는 “가장 가깝다”는 용어는 모델링 상황에 따라 KL 다이버전스, 로그우도 최대화, MSE 등으로 구체화됩니다.
• Priors(사전 지식)는 모델의 편향(bias)을 일종의 ‘약간의 가정’ 형태로 넣는 것인데, 가정이 단순할수록 모델이 제한될 수 있고, 가정이 복잡해질수록 학습 난이도도 올라갑니다.

3. How to train generative models?

[1] 최대우도 학습(MLE: Maximum Likelihood Estimation)

가장 먼저 최대우도 학습 아이디어부터 알아봅시다.
데이터 $D = \{x^{(1)}, x^{(2)}, \dots, x^{(m)}\}$가 주어졌을 때, 우리가 원하는 모델의 파라미터 $\theta$를 찾는 과정입니다.

• 목표

  $\max_{\theta} \ \frac{1}{|D|} \sum_{x \in D} \log p_{\theta}(x)$
  • 즉, 데이터가 나올 확률(likelihood)을 최대화하는 $\theta$를 찾습니다.
  • 로그를 씌운 뒤 합을 취하면, 곱셈(우도)을 쉽게 다룰 수 있게 됩니다.

• 직관

  • 관측된 모든 $x \in D$를 잘 설명(확률이 크게)하는 $\theta$를 찾는다.
  • 확률 모델에서 자주 쓰이는 대표적인 파라미터 추정 방법입니다.

[2] 잠재변수(latent 변수) 모델

위의 최대우도 학습은 모든 변수(피처)가 관측된 경우 상대적으로 단순합니다.
그런데 실제로는 관측되지 않은 변수(= 잠재 변수, hidden/latent)가 있을 때가 많습니다.

• 예시
  • 클러스터링: 군집 레이블이 관측되지 않음
  • Unsupervised 학습: 어떤 특성이 숨어 있을지 모름

이처럼 잠재변수 모델을 쓰면:
1. 복잡한 분포 $p(x)$를 단순한 조건부 분포 $p(x \mid z)$의 묶음으로 표현 가능
2. 다양한 비지도 학습(representation learning 등)에 활용 용이

단점은?

• No Free Lunch: 실제로는 학습이 훨씬 복잡해집니다.

[3] 마진Likelihood(주변우도)와 부분 관측 데이터(Partially Observed Data)

3.1 주변우도(Marginal Likelihood)

잠재 변수가 있는 경우, 우리가 원하는 것은 결국 $p_{\theta}(x)$입니다.
하지만 잠재 변수 $z$가 관측되지 않는다면,

이렇게 $z$에 대해 모두 합(적분)해야 합니다.

• 문제점
  • $z$가 이산형이고 $z \in \{0,1\}^{30}$라면 $2^{30}$개 경우의 수!
  • 연속형이라면 적분이 복잡하여 닫힌형 해를 구하기 어려움.
  • 결과적으로 우도를 계산하기가 매우 비싸집니다.

3.2 부분 관측 데이터 문제

• 실제 데이터에서 일부 픽셀이 가려지거나, 잠재 변수들이 아예 관측되지 않는 상황.
• $\log \sum_{z} p(x,z;\theta)$ 형태의 항을 매 데이터마다 계산해야 함 → 연산량 폭발.
• 따라서 근사 기법(Approximation)이 필수적!

[4] 근사 기법 1: Naive Monte Carlo

가장 단순한(첫 번째) 시도는 몬테 카를로(Monte Carlo) 샘플링 기법을 쓰는 것입니다.

1. $z$를 가능한 값 전체에서 일부만 샘플한다고 가정
   • 예: $z^{(1)}, z^{(2)}, \dots, z^{(k)}$를 무작위로 뽑음
2. 샘플 평균으로 $\sum_z p_\theta(x,z)$를 근사
   $\sum_{z} p_{\theta}(x, z) \approx |Z| \cdot \frac{1}{k} \sum_{j=1}^k p_{\theta}(x, z^{(j)})$
   • $|Z|$는 $z$의 전체 가능한 경우의 수를 의미(이산형일 때).
   • $\frac{1}{k}\sum_j p_{\theta}(x, z^{(j)})$가 $\mathbb{E}[p_{\theta}(x,z)]$에 대한 표본평균.

• 장점

  • 구현이 쉽고, 아이디어가 직관적.

• 단점

  • $z$의 공간이 매우 큰 경우, 샘플 수 $k$를 크게 잡아야 정확도가 확보됨.
  • 이는 계산량 문제가 되어 이 방법만으로는 비효율일 수 있음.

[4] 근사기법 2 : 중요도 샘플링(Importance Sampling)

(1) 아이디어

우리가 구하고 싶은 $p_\theta(x)$를 직접 합(적분)하기 어렵다면,
'중요도 분포'로 불리는 다른 분포 $q(z)$를 도입해, 아래처럼 쓰는 방법이 있습니다:

즉, $q(z)$라는 분포에서 샘플을 뽑은 뒤, $\frac{p_\theta(x,z)}{q(z)}$를 평균 내는 방식으로 $p_\theta(x)$를 근사하는 것입니다.

(2) 중요도 몬테 카를로 근사

샘플링

1. $z^{(1)}, z^{(2)}, \dots, z^{(k)}$를 (가능한) $z$의 공간에서 $q(z)$로부터 무작위로 샘플한다.

근사

2. 아래 식으로 $p_\theta(x)$를 추정한다:

• 이렇게 하면, 모든 $z$에 대해 합을 하지 않고도,
  $k$개의 샘플만으로 $p_\theta(x)$를 근사할 수 있습니다.

(3) $q(z)$는 어떻게 고르나?

중요도 샘플링에서 핵심은 $q(z)$를 잘 선택해야 한다는 점입니다.

• 너무 분산이 큰 샘플(즉, $p_\theta(x,z)/q(z)$가 들쑥날쑥하면) 근사가 잘 안 될 수 있습니다.
• 너무 좁은 분포를 쓰면, 중요한 $z$값들을 놓칠 수 있습니다.

이상적으로는 $q(z)$가 후방 분포 $p(z \mid x)$에 가깝도록 고르는 것이 좋습니다.

• $p(z \mid x)$가 크다 = 관측된 $x$를 잘 설명하는 $z$
• 이 근처를 자주 샘플링하면, $\frac{p_\theta(x,z)}{q(z)}$가 안정적으로 작동

하지만 실제로 $p(z \mid x)$ 자체도 구하기 어려운 경우가 많습니다.

• 그렇다면 어떻게 $q(z)$를 만들고, 학습할까요?

[4] 세 번째 시도: 변분 추론(Variational Inference)

(1) 직관

• 문제: $p(z\mid x)$를 직접 계산하거나, KL$(\,q(z)\mid p(z\mid x)\!)$ 등을 직접 최적화하려면 $p(x)$를 알아야 하는데, 이것도 마찬가지로 어려움.
• 아이디어: $q(z;\phi)$라는 파라미터화된 분포(예: 가우시안, 베르누이 등)를 설정하고,
  $\phi$(=변분 파라미터)를 최적화해서 $p(z \mid x)$를 가장 근사하도록 한다.

예를 들어, $q(z;\phi)$를

• 평균 $\phi_1$, 공분산(분산) $\phi_2$를 갖는 가우시안으로 잡는다고 해봅시다.
• $\phi$를 잘 조정하면, $p(z\mid x;\theta)$ 모양과 최대한 비슷해집니다.

(2) 최적화 문제

우리는

를 풀고 싶습니다.
하지만 이는 여전히 $\log p(x)$를 알아야 해서 직접 풀 수가 없습니다.

증거 하한(Evidence Lower Bound, ELBO)

KL을 직접 최소화하는 대신,
ELBO라는 다른 손실 함수를 최대화하면,
결과적으로 같은 목적을 달성할 수 있음을 보입니다:

이 식을 재배열하면,

• 이 오른쪽 식을 ELBO라 부릅니다.
• $q(z)$(또는 $\phi$)를 학습하여, 이 ELBO를 최대화하면,
  결국 $\text{KL}\bigl(q(z)\,\|\,p(z\mid x)\bigr)$를 낮추게 됩니다.

(3) 결론

• 중요도 샘플링에서는 $q(z)$를 잘 골라야 하는데, 직접 골라 쓰기 힘든 경우가 많습니다.
• 변분 추론에서는 $q(z;\phi)$를 스스로 학습(최적화)하여, $p(z\mid x)$를 근사하게 만듭니다.
• 이 과정을 통해 $p_\theta(x)$ 계산도 간접적으로 해결할 수 있고, 대규모 데이터에서도 빠른 근사가 가능해집니다.

요약

1. 중요도 샘플링:

   • $p_\theta(x) = \mathbb{E}_{z\sim q(z)}[\frac{p_\theta(x,z)}{q(z)}]$
   • $q(z)$가 중요! → 가능한 한 $p(z\mid x)$에 가까워야 분산이 적어짐.

2. 변분 추론:

   • $q(z;\phi)$를 파라미터화하고, ELBO를 최대화하여 $p(z\mid x)$ 근사.
   • $\log p(x)$를 직접 계산하기 어려운 문제를, 최적화 문제로 전환.

3. 의의:

   • 부분 관측(혹은 잠재 변수) 문제에서 생성 모델을 학습할 때,
   • 우도를 근사하고 후방 분포를 추정하는 핵심 아이디어로 널리 쓰임.

정리

1. 최대우도 학습: 우리가 얻은 데이터 확률을 최대로 만드는 모델 파라미터 $\theta$ 찾기.
2. 잠재변수 모델: 관측되지 않은 변수를 모델 내부에 두어 표현력을 높이지만, 계산이 복잡해짐.
3. 마진Likelihood: $p_{\theta}(x) = \sum_z p_{\theta}(x,z)$ 형태라 직접 계산이 난해.
4. Naive Monte Carlo: 일부 $z$ 샘플을 뽑아 우도를 근사. 간단하지만 큰 공간에서 비효율.

위 내용을 통해 부분 관측 데이터나 잠재변수가 포함된 복잡한 생성 모델에서도,
어떻게든 우도를 최대화하려면 결국 근사 기법이 필요함을 알 수 있습니다.

[5] 변분 추론(Variational Inference) 개념과 ELBO 도입

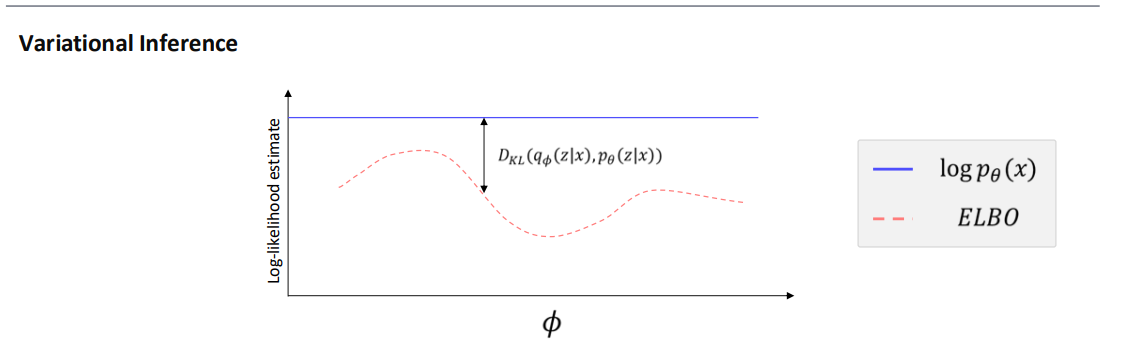
1. 로그 우도와 ELBO

   • 파란색 실선으로 표시된 $\log p_\theta(x)$는 우리가 최대화하고 싶은 “진짜” 데이터의 로그 가능도(log-likelihood)입니다.
   • 빨간색 점선으로 표시된 ELBO(Evidence Lower BOund)는 $\log p_\theta(x)$의 하한(lower bound) 역할을 합니다.

2. KL 발산(KL Divergence)

   • 두 확률분포 $q_\phi(z|x)$와 $p_\theta(z|x)$ 간의 차이를 나타내는 척도가 바로 $\mathrm{D}_{\mathrm{KL}}(q_\phi(z|x)\|p_\theta(z|x))$입니다.
   • $\mathrm{D}_{\mathrm{KL}}$이 작아질수록 $q_\phi(z|x)$가 참 후분포 $p_\theta(z|x)$를 잘 근사하게 되고, 결과적으로 ELBO와 $\log p_\theta(x)$ 사이의 차이가 줄어듭니다.

즉, “$q_\phi$가 posterior를 잘 근사할수록” ELBO가 “진짜 로그 우도”에 가까워집니다.

[6] ELBO 최적화를 통한 $\theta$와 $\phi$의 동시 학습

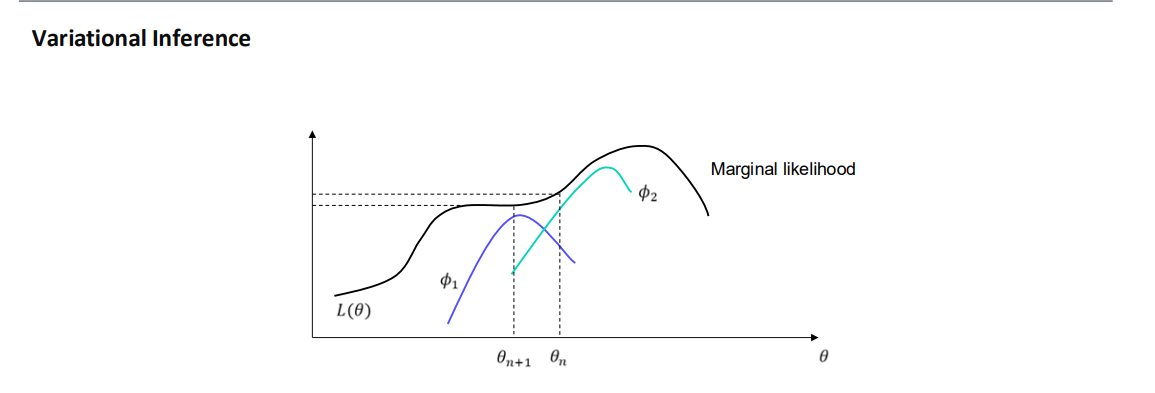
• $\theta$는 생성 모델(Generator)의 파라미터, $\phi$는 근사 posterior(Variational Distribution)의 파라미터입니다.
• $\theta$만 최적화하는 것이 아니라, $\phi$도 함께 최적화해 ELBO를 최대화(maximize)하는 과정을 거칩니다.
• 그림에서 $\phi_1, \phi_2$가 각각 다른 Variational Distribution을 나타내고, 각 $\phi$에 대해 구한 하한 $L(x; \theta, \phi)$도 서로 다르게 나타납니다.
• 우리는 $\theta$와 $\phi$를 동시에 갱신하면서 점차 “마진널 가능도(marginal likelihood)”에 근접하도록 만듭니다.

[7] ELBO의 해석

• ELBO는 다음과 같은 형태를 가집니다.
  $L = \sum_{z} q(z) \log p(z, x; \theta) + H(q)$
  여기서 $H(q)$는 $q(z)$의 엔트로피(entropy)로, 분포 $q(z)$가 얼마나 퍼져 있는지를 나타내는 항입니다.
• 왼쪽 그림에서 $p(x,z)$는 참 분포(데이터와 잠재 변수를 함께 고려)이고, $q^*(z|x)$는 근사 posterior입니다.
• $\mathrm{H} = -\infty$부터 점점 커질수록 분포 $q(z)$가 퍼져서 엔트로피가 커지는 모습을 볼 수 있습니다.

(8) 정리

1. ELBO = $\log p_\theta(x)$에 대한 하한 역할을 한다.
2. KL 발산을 줄이는 방향(즉, $q_\phi(z|x)$가 $p_\theta(z|x)$를 잘 맞추는 방향)으로 $\phi$를 학습한다.
3. $\theta$와 $\phi$를 동시에 최적화하여 데이터의 마진널 가능도(evidence)에 근접한다.

1. Partially Observed Data의 로그-우도( Log-Likelihood ) 계산의 어려움

• 부분 관측 데이터(Partially Observed Data)에 대한 모델의 우도(Likelihood)를 계산하려고 할 때,
  $\log \left(\sum_{z \in \mathcal{Z}} p_\theta(x, z)\right)$
  는 직접적으로 계산하기가 어렵다.
• 이 때 임의의 분포 $q(z)$를 도입하여,
  $\log \left(\sum_{z \in \mathcal{Z}} \frac{q(z)}{q(z)} p_\theta(x, z)\right) = \log \left(\mathbb{E}_{z \sim q(z)}\left[\frac{p_\theta(x,z)}{q(z)}\right]\right)$
  처럼 표현할 수 있다.
• 하지만 여전히 이 로그 안에 있는 기댓값(Expectation)을 직접 최적화하기는 쉽지 않다.

2. Jensen's Inequality ( concave 함수에 대한 부등식 )

• $\log(\cdot)$는 오목(concave) 함수이므로, Jensen's Inequality를 적용할 수 있다.
• Jensen's Inequality(오목 함수 버전)
  $\log \left(\mathbb{E}_{z \sim q(z)}[f(z)]\right) \;\;\ge\;\; \mathbb{E}_{z \sim q(z)}[\log(f(z))].$
• 이 때 $f(z)$를 적절히 설정하여, ELBO(Evidence Lower BOund)의 형태로 유도한다.
• 보통 $f(z) = \frac{p_\theta(x,z)}{q(z)}$ 로 두게 되면,
  $\log \Bigl(\mathbb{E}_{z \sim q(z)}\bigl[\frac{p_\theta(x,z)}{q(z)}\bigr]\Bigr) \;\;\ge\;\; \mathbb{E}_{z \sim q(z)}\Bigl[\log \bigl(\frac{p_\theta(x,z)}{q(z)}\bigr)\Bigr].$

3. ELBO( Evidence Lower Bound )의 정의 및 해석

• 위 부등식을 다시 정리하면,
  $\log p_\theta(x) = \log\Bigl(\sum_z p_\theta(x,z)\Bigr) \;\;\ge\;\; \mathbb{E}_{z \sim q(z)} \left[\log p_\theta(x,z) - \log q(z)\right].$
• 여기서 우변(우도의 하한)을 ELBO라 부르고, 다음과 같이 표기한다:
  $\text{ELBO}(q) = \mathbb{E}_{z \sim q(z)}[\log p_\theta(x,z)] \;-\; \mathbb{E}_{z \sim q(z)}[\log q(z)].$
• 이를 또 다른 형태로 분해하면,
  $\text{ELBO}(q) = \underbrace{\mathbb{E}_{z \sim q(z)}[\log p_\theta(x \mid z)]}_{\text{Likelyhood term}} \;-\; \underbrace{\text{KL}\bigl(q(z) \;\|\; p(z)\bigr)}_{\text{Prior term}}$
  와 같은 식으로 해석할 수 있다 (중간 과정에서 $\log p(x,z) = \log p(x \mid z) + \log p(z)$를 활용).

4. Auto-Encoding Variational Bayes (VAE) 구조 개요

• VAE(Variational Autoencoder)는 인코더와 디코더로 구성된 확률적 생성 모델이다.
• 인코더(Encoder)
  • $q_\phi(z \mid x)$ 로 표기하며, 관측 데이터 $x$를 잠재 변수 $z$의 분포로 매핑한다.
  • 보통 뉴럴넷으로 $\mu(x), \sigma(x)$ 같은 파라미터를 예측해, 가우시안 분포 $\mathcal{N}(z; \mu(x), \sigma^2(x)I)$에서 샘플링하는 식으로 구현된다.
• 디코더(Decoder)
  • $p_\theta(x \mid z)$ 로 표기하며, 잠재 변수 $z$로부터 원본 데이터 $x$를 복원(혹은 생성)한다.
• 이 때, 잠재 분포(Latent distribution)는 $q_\phi(z \mid x)$이며, 사전분포(Prior)는 보통 $\mathcal{N}(0, I)$와 같은 단순한 분포 $p(z)$로 두는 것이 일반적이다.

5. VAE의 학습 목표: ELBO 최적화

• VAE의 학습 목표($\mathcal{L}(x;\theta,\phi)$)는 결국 ELBO를 최대화하는 것이다.

• 공식

  $\mathcal{L}(x;\theta,\phi) = \mathbb{E}_{q_\phi(z \mid x)} \big[\log p_\theta(z,x) - \log q_\phi(z \mid x)\big].$

• 이를 좀 더 풀어서 쓰면,

  $\mathcal{L}(x;\theta,\phi) = \mathbb{E}_{q_\phi(z \mid x)} [\log p_\theta(x \mid z) + \log p_\theta(z)] \;\;-\;\; \mathbb{E}_{q_\phi(z \mid x)} [\log q_\phi(z \mid x)].$

• 결과적으로는

  $\mathcal{L}(x;\theta,\phi) = \underbrace{\mathbb{E}_{q_\phi(z \mid x)} [\log p_\theta(x \mid z)]}_{\text{재구성 항(reconstruction term)}} \;-\; \underbrace{\text{KL}\bigl(q_\phi(z \mid x)\;\|\;p(z)\bigr)}_{\text{정규화 항(regularization term)}}$

  로 많이 알려져 있다.

  

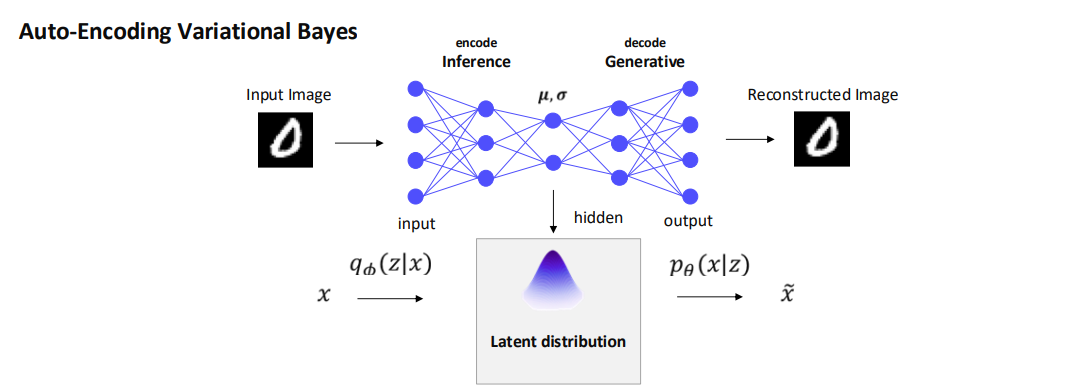
6. VAE의 동작 과정

1. 입력 데이터 $\mathbf{x}^i$를 준비한다.
2. 인코더 $q_\phi(z \mid \mathbf{x}^i)$에서 잠재변수 $\mathbf{z}$를 샘플링한다.
3. 디코더 $p_\theta(x \mid \mathbf{z})$에서 샘플링하여, $\mathbf{x}^i$와 유사한 $\hat{\mathbf{x}}$ (재구성된 이미지/데이터)를 얻는다.

7. VAE 훈련 목표(직관적 해석)

• 재구성 항(Reconstruction Term): $\hat{x}$가 원본 $x$와 유사해지도록(=$p_\theta(x\mid z)$가 크도록) 만든다.
• 정규화 항(Prior Regularization Term): 잠재변수 $z$가 미리 정한 사전분포 $p(z)$에 가깝도록(=KL이 작도록) 만든다.
• 따라서, 재구성 능력과 잠재 변수의 일반성(regularization)을 균형 있게 맞추는 것이 목적이다.

종합 요약

1. Partially Observed Data에서 $\log p_\theta(x)$ (즉, $\log \sum_z p_\theta(x,z)$)를 직접 계산하기 어려우므로, 분포 $q(z)$를 사용해 Jensen's Inequality로 하한(ELBO)를 구한다.

2. 이 ELBO는 $\log p_\theta(x)$의 하한이 되며, VAE(Variational Autoencoder)에서는 이를 최대화(학습)하는 방식으로 인코더와 디코더 파라미터($\theta,\phi$)를 최적화한다.

3. 최적화의 결과, 재구성 에러를 줄이면서(데이터 복원 능력) 잠재변수 공간에서는 사전분포와 유사하게(일반화 능력) 만드는 모델을 얻게 된다.