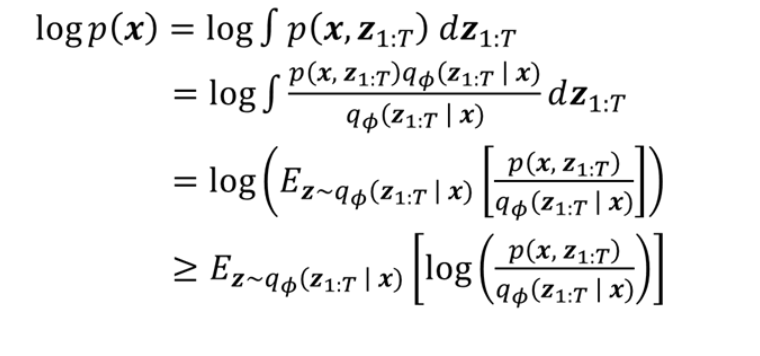1. Recap
(1). Latent Variable Models
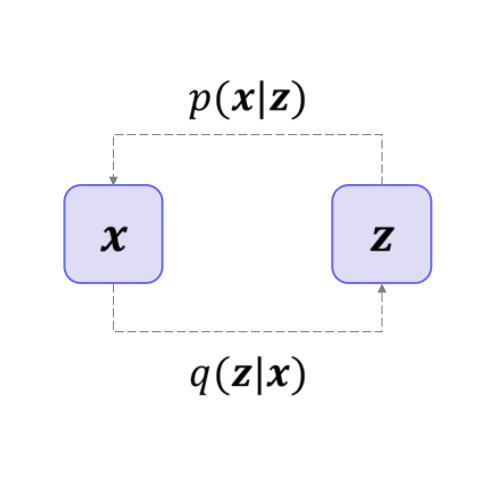
잠재변수 모델은 관측 데이터 x \mathbf{x} x 잠재 변수 z \mathbf{z} z p ( x ) p(\mathbf{x}) p ( x ) p ( x ∣ z ) p(\mathbf{x} \mid \mathbf{z}) p ( x ∣ z )
주요 특징
복잡한 모델링을 단순화
직접 x \mathbf{x} x z \mathbf{z} z p ( x ) = ∫ p ( x ∣ z ) p ( z ) d z p(\mathbf{x}) = \int p(\mathbf{x} \mid \mathbf{z})\,p(\mathbf{z})\,d\mathbf{z} p ( x ) = ∫ p ( x ∣ z ) p ( z ) d z
비지도 학습에 유리
클러스터링, 표현 학습, 생성 모델 등에서 잠재 변수를 통해 데이터의 잠재 구조 를 학습할 수 있습니다.
학습 난이도 (No free lunch)
잠재 변수가 관측되지 않으므로, 완전히 관측된 모델에 비해 학습 과정이 더 복잡 합니다.
보통 최대가능도 추정(EM 알고리즘), 변분 추론(ELBO), MCMC 등 다양한 기법이 필요합니다.
(2). Hierarchical Variational Autoencoders
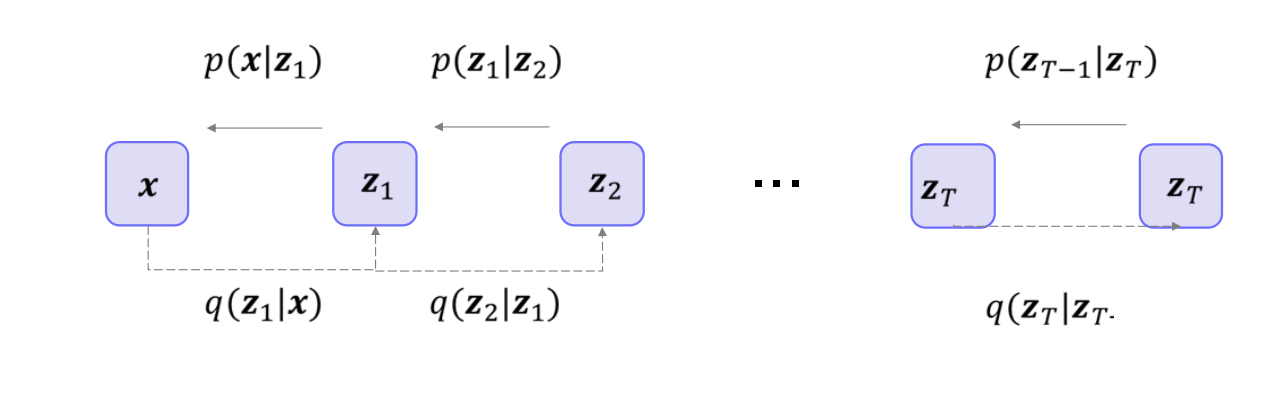
정의 잠재 변수를 여러 개의 층위(hierarchy) 로 쌓아서 표현합니다.z z z z 1 , z 2 , … , z L z_1, z_2, \dots, z_L z 1 , z 2 , … , z L
왜 여러 층위(hierarchies)를 쓰나?
복잡한 데이터 구조 를 더 잘 표현하기 위해
예를 들어, 사람 얼굴 이미지를 모델링할 때,
첫 번째 잠재 변수가 전반적인 형태 (예: 얼굴 윤곽)을,
두 번째 잠재 변수가 세부 특성 (예: 눈, 코, 입 배치)을,
세 번째 잠재 변수가 더 미세한 특징 (예: 주근깨, 표정)계층적으로 특징을 분리해서 나타낼 수 있습니다.
더 풍부한 표현력
단일 층위의 VAE보다 훨씬 복잡하고 세밀한 분포를 학습할 수 있습니다.
어떻게 동작하나?
인코더(Encoder)
입력 x x x
예: q ϕ ( z L ∣ x ) , q ϕ ( z L − 1 ∣ x , z L ) , … q_{\phi}(z_L \mid x), \; q_{\phi}(z_{L-1} \mid x, z_L), \;\dots q ϕ ( z L ∣ x ) , q ϕ ( z L − 1 ∣ x , z L ) , …
위에서부터 차례대로 잠재 변수를 샘플링해 내려가는 구조입니다.
디코더(Decoder)
마지막 층위부터 순차적으로(혹은 동시에) 잠재 변수들을 입력받아, 최종적으로 x x x
예: p θ ( x ∣ z 1 , z 2 , … , z L ) p_{\theta}(x \mid z_1, z_2, \dots, z_L) p θ ( x ∣ z 1 , z 2 , … , z L )
상위 층위의 z z z z z z
학습 (ELBO 최적화)
일반 VAE와 마찬가지로, 증거 하한(ELBO) 을 최대화하는 방식으로 학습합니다.
다만 다층 구조 때문에, ELBO 역시 여러 층위의 KL 발산 항 등을 포함하게 됩니다.
+추가) HVAE의 ELBO
log p ( x ) \log p(\mathbf{x}) log p ( x )
log p ( x ) = log ∫ p ( x , z 1 : T ) d z 1 : T . \log p(\mathbf{x}) = \log \int p(\mathbf{x}, \mathbf{z}_{1:T}) \, d\mathbf{z}_{1:T}. log p ( x ) = log ∫ p ( x , z 1 : T ) d z 1 : T .
z 1 : T \mathbf{z}_{1:T} z 1 : T z 1 , z 2 , … , z T \mathbf{z}_1, \mathbf{z}_2, \dots, \mathbf{z}_T z 1 , z 2 , … , z T
임의의 분포 q ϕ ( z 1 : T ∣ x ) q_{\phi}(\mathbf{z}_{1:T} \mid \mathbf{x}) q ϕ ( z 1 : T ∣ x )
log p ( x ) = log ∫ p ( x , z 1 : T ) q ϕ ( z 1 : T ∣ x ) q ϕ ( z 1 : T ∣ x ) d z 1 : T . \log p(\mathbf{x}) = \log \int \frac{p(\mathbf{x}, \mathbf{z}_{1:T}) \, q_{\phi}(\mathbf{z}_{1:T} \mid \mathbf{x})} {q_{\phi}(\mathbf{z}_{1:T} \mid \mathbf{x})} \, d\mathbf{z}_{1:T}. log p ( x ) = log ∫ q ϕ ( z 1 : T ∣ x ) p ( x , z 1 : T ) q ϕ ( z 1 : T ∣ x ) d z 1 : T .
분모·분자를 q ϕ ( z 1 : T ∣ x ) q_{\phi}(\mathbf{z}_{1:T} \mid \mathbf{x}) q ϕ ( z 1 : T ∣ x )
기댓값 형태로 표현
= log E z 1 : T ∼ q ϕ ( z 1 : T ∣ x ) [ p ( x , z 1 : T ) q ϕ ( z 1 : T ∣ x ) ] . = \log \mathbb{E}_{\mathbf{z}_{1:T} \sim q_{\phi}(\mathbf{z}_{1:T} \mid \mathbf{x})} \biggl[ \frac{p(\mathbf{x}, \mathbf{z}_{1:T})}{q_{\phi}(\mathbf{z}_{1:T} \mid \mathbf{x})} \biggr]. = log E z 1 : T ∼ q ϕ ( z 1 : T ∣ x ) [ q ϕ ( z 1 : T ∣ x ) p ( x , z 1 : T ) ] .
Jensen's Inequality 적용 → ELBO 하한
log E z 1 : T ∼ q ϕ ( z 1 : T ∣ x ) [ … ] ≥ E z 1 : T ∼ q ϕ ( z 1 : T ∣ x ) [ log ( p ( x , z 1 : T ) q ϕ ( z 1 : T ∣ x ) ) ] . \log \mathbb{E}_{\mathbf{z}_{1:T} \sim q_{\phi}(\mathbf{z}_{1:T} \mid \mathbf{x})} \bigl[\dots\bigr] \;\;\ge\;\; \mathbb{E}_{\mathbf{z}_{1:T} \sim q_{\phi}(\mathbf{z}_{1:T} \mid \mathbf{x})} \Bigl[ \log \bigl(\frac{p(\mathbf{x}, \mathbf{z}_{1:T})}{q_{\phi}(\mathbf{z}_{1:T} \mid \mathbf{x})}\bigr) \Bigr]. log E z 1 : T ∼ q ϕ ( z 1 : T ∣ x ) [ … ] ≥ E z 1 : T ∼ q ϕ ( z 1 : T ∣ x ) [ log ( q ϕ ( z 1 : T ∣ x ) p ( x , z 1 : T ) ) ] .
이를 다시 풀어서 쓰면,
log p ( x ) ≥ E z 1 : T ∼ q ϕ ( z 1 : T ∣ x ) [ log p ( x , z 1 : T ) ] ⏟ 우도 항 − E z 1 : T ∼ q ϕ ( z 1 : T ∣ x ) [ log q ϕ ( z 1 : T ∣ x ) ] ⏟ 엔트로피(또는 정규화) 항 \log p(\mathbf{x}) \;\;\ge\;\; \underbrace{ \mathbb{E}_{\mathbf{z}_{1:T}\sim q_\phi(\mathbf{z}_{1:T}\mid \mathbf{x})} [\log p(\mathbf{x},\mathbf{z}_{1:T})] }_{\text{우도 항}} \;-\; \underbrace{ \mathbb{E}_{\mathbf{z}_{1:T}\sim q_\phi(\mathbf{z}_{1:T}\mid \mathbf{x})} [\log q_\phi(\mathbf{z}_{1:T}\mid \mathbf{x})] }_{\text{엔트로피(또는 정규화) 항}} log p ( x ) ≥ 우도 항 E z 1 : T ∼ q ϕ ( z 1 : T ∣ x ) [ log p ( x , z 1 : T ) ] − 엔트로피 ( 또는 정규화 ) 항 E z 1 : T ∼ q ϕ ( z 1 : T ∣ x ) [ log q ϕ ( z 1 : T ∣ x ) ] 이를 ELBO(증거 하한) 라고 하며, HVAE에서는 z 1 : T \mathbf{z}_{1:T} z 1 : T
2. 해석
p ( x , z 1 : T ) p(\mathbf{x}, \mathbf{z}_{1:T}) p ( x , z 1 : T ) x \mathbf{x} x z 1 : T \mathbf{z}_{1:T} z 1 : T q ϕ ( z 1 : T ∣ x ) q_{\phi}(\mathbf{z}_{1:T} \mid \mathbf{x}) q ϕ ( z 1 : T ∣ x ) x \mathbf{x} x z 1 : T \mathbf{z}_{1:T} z 1 : T ELBO : L ( x ; ϕ , θ ) = E q ϕ ( z 1 : T ∣ x ) [ log p θ ( x , z 1 : T ) − log q ϕ ( z 1 : T ∣ x ) ] . \mathcal{L}(\mathbf{x}; \phi, \theta) = \mathbb{E}_{q_{\phi}(\mathbf{z}_{1:T}\mid \mathbf{x})} \bigl[ \log p_{\theta}(\mathbf{x}, \mathbf{z}_{1:T}) - \log q_{\phi}(\mathbf{z}_{1:T}\mid \mathbf{x}) \bigr]. L ( x ; ϕ , θ ) = E q ϕ ( z 1 : T ∣ x ) [ log p θ ( x , z 1 : T ) − log q ϕ ( z 1 : T ∣ x ) ] .
여기서 z 1 : T \mathbf{z}_{1:T} z 1 : T log p θ ( x , z 1 : T ) \log p_{\theta}(\mathbf{x}, \mathbf{z}_{1:T}) log p θ ( x , z 1 : T ) log p θ ( x ∣ z 1 , … , z T ) + log p θ ( z 1 : T ) \log p_{\theta}(\mathbf{x} \mid \mathbf{z}_1, \dots, \mathbf{z}_T) + \log p_{\theta}(\mathbf{z}_{1:T}) log p θ ( x ∣ z 1 , … , z T ) + log p θ ( z 1 : T )
log q ϕ ( z 1 : T ∣ x ) \log q_{\phi}(\mathbf{z}_{1:T}\mid \mathbf{x}) log q ϕ ( z 1 : T ∣ x ) ( z l ∣ z l + 1 , … ) (z_{l}\mid z_{l+1},\dots) ( z l ∣ z l + 1 , … )
3. 요점 정리
Hierarchical VAE(HVAE) 에서는 잠재변수 z \mathbf{z} z z 1 : T \mathbf{z}_{1:T} z 1 : T ELBO 를 유도하는 기본 방식(log p ( x ) \log p(\mathbf{x}) log p ( x ) 잠재변수를 적분(또는 합)하는 범위 가 z 1 , … , z T \mathbf{z}_{1}, \dots, \mathbf{z}_{T} z 1 , … , z T 그 결과, 복잡한 z 1 : T \mathbf{z}_{1:T} z 1 : T 를 모델링하기 위한 ELBO 가 자연스럽게 도출되며, 이는 여러 KL term, 혹은 여러 조건부 분포 항을 포함하게 됩니다.
장점 & 단점
장점
(1) 복잡한 데이터 를 더 잘 모델링 가능
(2) 계층적 표현 학습 : 레이어별로 데이터의 추상화 수준이 달라짐
단점
(1) 구조가 복잡해 학습 난이도가 높음
(2) 계산 비용이 증가: 여러 층위를 거치므로 파라미터 수도 많아짐
결론
HVAE는 잠재 변수의 다층 구조 를 통해 데이터를 더 풍부하고 계층적으로 표현할 수 있는 방법입니다.더 복잡한 분포 를 학습하게 만든 모델이라고 이해할 수 있습니다.
2. Variational Diffusion Model
(1). Variational Diffusion Model
VDM은 기본적으로 Markovian HVAE (Hierarchical VAE)의 한 형태로 볼 수 있습니다. 다만, 다음 세 가지 핵심 제약 을 둠으로써 “Diffusion”(확산) 과정을 활용 하는 모델이 됩니다:
잠재 공간의 차원 이 데이터 차원과 동일 하다.
q ( z 1 : T ∣ x ) = q ( z 1 ∣ x ) ∏ t = 2 T q ϕ ( z t ∣ z t − 1 ) q(z_{1:T} \mid x) = q(z_1 \mid x)\,\prod_{t=2}^T q_\phi\bigl(z_t \mid z_{t-1}\bigr) q ( z 1 : T ∣ x ) = q ( z 1 ∣ x ) t = 2 ∏ T q ϕ ( z t ∣ z t − 1 ) can be rewritten as:
q ( x 1 : T ∣ x 0 ) = ∏ t = 1 T q ϕ ( x t ∣ x t − 1 ) . q(x_{1:T} \mid x_0) = \prod_{t=1}^T q_\phi\bigl(x_t \mid x_{t-1}\bigr). q ( x 1 : T ∣ x 0 ) = t = 1 ∏ T q ϕ ( x t ∣ x t − 1 ) .
각 타임스텝에서의 잠재 인코더 구조 는 학습되지 않으며, 선형 가우시안(linear Gaussian) 형태 로 고정 된다.
즉, 아래와 같은 형태를 가정합니다: q ( x t ∣ x t − 1 ) = N ( x t ; α t x t − 1 , ( 1 − α t ) I ) , q(x_t \mid x_{t-1}) = \mathcal{N}\bigl(x_t \; ; \; \sqrt{\alpha_t} x_{t-1} \;, (1-\alpha_t) I\bigr), q ( x t ∣ x t − 1 ) = N ( x t ; α t x t − 1 , ( 1 − α t ) I ) , x t − 1 x_{t-1} x t − 1 x t x_t x t
최종 타임스텝 T T T 잠재 변수(또는 데이터)가 표준 정규분포 (standard Gaussian)가 되도록 α t \alpha_t α t α t \alpha_t α t p ( x 0 : T ∣ x t − 1 ) = p ( x T ) ∏ t = 1 T p θ ( x t − 1 ∣ x t ) p(x_{0:T} \mid x_{t-1}) = p(x_T)\,\prod_{t=1}^T p_\theta\bigl(x_{t-1} \mid x_t\bigr) p ( x 0 : T ∣ x t − 1 ) = p ( x T ) t = 1 ∏ T p θ ( x t − 1 ∣ x t )
where
p ( x T ) = N ( x T ; 0 , I ) . p(x_T) = \mathcal{N}(x_T \; ; \; 0, I). p ( x T ) = N ( x T ; 0 , I ) .
즉, 시간이 지남에 따라 노이즈가 점차 강해져서 마지막엔 완전한 가우시안 상태에 가까워진다는 설정입니다.
왜 이런 제약을 두나?
(1) 데이터 차원과 동일 :z z z 시간에 따라 “이미지(데이터)” 자체가 변형 되므로, 잠재 변수도 데이터와 같은 차원을 갖게 됩니다.
(2) 선형 가우시안 형태(학습 X) :노이즈를 섞는 과정 이 고정된 수식대로 진행된다고 가정하여, 모델이 학습해야 할 파라미터 를 크게 줄입니다. 대신 디코더(역방향 확산 과정) 가 학습의 주요 대상이 됩니다.(선형 가우시안”이라고 부르는 이유는, “가우시안 노이즈를 추가하는 규칙” 이 시간 t t t
(3) 표준 정규화로 귀결 :
마지막 스텝이 완전한 노이즈 상태(정규분포)라는 가정으로, 생성 과정(디노이징 역방향) 을 명확히 정의할 수 있습니다.
정리하면, Variational Diffusion Model(VDM) 은 Markovian HVAE 에 “시간에 따라 점진적으로 데이터에 노이즈를 추가하는 인코더”를 도입한 형태입니다. 이 노이즈 추가 과정은
데이터 차원 과 동일한 잠재공간에서고정된 선형 가우시안 수식 으로최종적으로 표준 가우시안 에 도달하도록이미지를 “노이즈 → 깨끗한 이미지” 방향으로 학습 (역방향 확산)하는 방식을 사용합니다.
(2). ELBO: 1st try
Diffusion Model(또는 Variational Diffusion Model, VDM)에서도, 다른 확률 생성 모델(예: HVAE)과 마찬가지로 ELBO 를 최대화하는 방식으로 학습할 수 있습니다.
1. log p ( x ) \log p(x) log p ( x )
우리가 구하고 싶은 것은 log p ( x ) \log p(x) log p ( x )
하지만 p ( x ) = ∫ p ( x 0 : T ) d x 1 : T p(x) = \int p(x_{0:T}) \, dx_{1:T} p ( x ) = ∫ p ( x 0 : T ) d x 1 : T x 1 : T x_{1:T} x 1 : T 직접 계산 이 매우 어렵습니다.
2. 보조 분포 q ( x 1 : T ∣ x 0 ) q(x_{1:T} \mid x_0) q ( x 1 : T ∣ x 0 )
아이디어
q ( x 1 : T ∣ x 0 ) q ( x 1 : T ∣ x 0 ) \frac{q(x_{1:T}\mid x_0)}{q(x_{1:T}\mid x_0)} q ( x 1 : T ∣ x 0 ) q ( x 1 : T ∣ x 0 ) p ( x 0 : T ) p(x_{0:T}) p ( x 0 : T ) 이처럼 q ( ⋅ ) q(\cdot) q ( ⋅ ) 기댓값 형태 로 바꾸어 ELBO를 유도합니다.
적분을 기댓값으로
log ∫ p ( x 0 : T ) d x 1 : T = log ∫ p ( x 0 : T ) q ( x 1 : T ∣ x 0 ) q ( x 1 : T ∣ x 0 ) d x 1 : T = log ( E q ( x 1 : T ∣ x 0 ) [ p ( x 0 : T ) q ( x 1 : T ∣ x 0 ) ] ) . \log \int p(x_{0:T}) \, dx_{1:T} = \log \int \frac{p(x_{0:T}) \, q(x_{1:T}\mid x_0)}{q(x_{1:T}\mid x_0)} \, dx_{1:T} = \log \Bigl( E_{q(x_{1:T}\mid x_0)} \bigl[ \frac{p(x_{0:T})}{q(x_{1:T}\mid x_0)} \bigr] \Bigr). log ∫ p ( x 0 : T ) d x 1 : T = log ∫ q ( x 1 : T ∣ x 0 ) p ( x 0 : T ) q ( x 1 : T ∣ x 0 ) d x 1 : T = log ( E q ( x 1 : T ∣ x 0 ) [ q ( x 1 : T ∣ x 0 ) p ( x 0 : T ) ] ) .
Jensen's Inequality
log E [ ⋅ ] ≥ E [ log ( ⋅ ) ] \log E[\cdot] \ge E[\log(\cdot)] log E [ ⋅ ] ≥ E [ log ( ⋅ ) ] 따라서log p ( x ) = log ∫ p ( x 0 : T ) d x 1 : T ≥ E q ( x 1 : T ∣ x 0 ) [ log p ( x 0 : T ) q ( x 1 : T ∣ x 0 ) ] . \log p(x) = \log \int p(x_{0:T})\, dx_{1:T} \;\ge\; E_{q(x_{1:T}\mid x_0)} \Bigl[\log \frac{p(x_{0:T})}{q(x_{1:T}\mid x_0)}\Bigr]. log p ( x ) = log ∫ p ( x 0 : T ) d x 1 : T ≥ E q ( x 1 : T ∣ x 0 ) [ log q ( x 1 : T ∣ x 0 ) p ( x 0 : T ) ] .
오른쪽 식이 바로 ELBO(증거 하한)의 형태가 됩니다.
3. ELBO의 구체적 형태
p ( x 0 : T ) p(x_{0:T}) p ( x 0 : T ) p ( x 0 ∣ x 1 ) p(x_0 \mid x_1) p ( x 0 ∣ x 1 ) p ( x t ∣ x t + 1 ) p(x_t \mid x_{t+1}) p ( x t ∣ x t + 1 ) q ( x 1 : T ∣ x 0 ) q(x_{1:T}\mid x_0) q ( x 1 : T ∣ x 0 ) E q ( x 1 : T ∣ x 0 ) [ log ( p ( x 0 : T ) q ( x 1 : T ∣ x 0 ) ) ] = E q [ log p ( x 0 ∣ x 1 ) ] − (KL 항들의 합) − … E_{q(x_{1:T}\mid x_0)}\Bigl[\log \bigl(\frac{p(x_{0:T})}{q(x_{1:T}\mid x_0)}\bigr)\Bigr] = E_{q}\bigl[\log p(x_0\mid x_1)\bigr] \;-\; \text{(KL 항들의 합)} \;-\; \dots E q ( x 1 : T ∣ x 0 ) [ log ( q ( x 1 : T ∣ x 0 ) p ( x 0 : T ) ) ] = E q [ log p ( x 0 ∣ x 1 ) ] − (KL 항들의 합 ) − … 이때 항들을 Likelihood(재구성 항) , Prior matching(KL 항) , Consistency 항 등으로 해석할 수 있습니다.
🤔어떻게 저렇게 3개로 딱 떨어지는 건가??
아예 처음부터 “왜 이렇게 식이 분해되고, 저항들이 어디서 나오는지”를 직관적으로 짚어보면 이해가 조금 더 쉬울것입니다. 핵심은 다음 두 가지 과정입니다.
확률분포를 전개(factorization)해서 분자와 분모를 쪼갠다. 쪼개진 로그항들을 다시 묶어서(혹은 재배치해서) KL 발산(KL divergence)이나 로그우도(log-likelihood) 형태로 정리한다.
아래에서는 이 과정을 단계별로 풀어서 설명하겠습니다.
1. 식의 시작: log p ( x 0 : T ) q ( x 1 : T ∣ x 0 ) \log\frac{p(x_{0:T})}{q(x_{1:T}\mid x_0)} log q ( x 1 : T ∣ x 0 ) p ( x 0 : T )
시작점이 되는 항은 다음과 같습니다.
log ( p ( x 0 : T ) q ( x 1 : T ∣ x 0 ) ) . \log\Bigl(\frac{p(x_{0:T})}{q(x_{1:T}\mid x_0)}\Bigr). log ( q ( x 1 : T ∣ x 0 ) p ( x 0 : T ) ) .
x 0 x_0 x 0 조건(관측) 이라 생각하고, x 1 : T x_{1:T} x 1 : T 숨겨진(잠재) 시계열 변수 로 생각할 수 있습니다.p ( x 0 : T ) p(x_{0:T}) p ( x 0 : T ) q ( x 1 : T ∣ x 0 ) q(x_{1:T}\mid x_0) q ( x 1 : T ∣ x 0 )
즉, log ( p / q ) \log\bigl(p/q\bigr) log ( p / q ) “진짜(모델) 분포와 근사(변분) 분포가 얼마나 다른가” 를 드러내는 표현입니다.
2. 분자(p ( x 0 : T ) p(x_{0:T}) p ( x 0 : T ) q ( x 1 : T ∣ x 0 q(x_{1:T}\mid x_0 q ( x 1 : T ∣ x 0 어떻게 쪼갰나?
식에서 보면 분자가 이렇게 되어 있습니다.
p ( x 0 : T ) = p ( x T ) p θ ( x 0 ∣ x 1 ) ∏ t = 1 T − 1 p θ ( x t ∣ x t + 1 ) . p(x_{0:T}) = p(x_T)\,p_\theta\bigl(x_0 \mid x_1\bigr)\,\prod_{t=1}^{T-1}p_\theta\bigl(x_t \mid x_{t+1}\bigr). p ( x 0 : T ) = p ( x T ) p θ ( x 0 ∣ x 1 ) t = 1 ∏ T − 1 p θ ( x t ∣ x t + 1 ) . 그리고 분모는
q ( x 1 : T ∣ x 0 ) = q ( x T ∣ x T − 1 ) ∏ t = 1 T − 1 q ( x t ∣ x t − 1 ) . q(x_{1:T} \mid x_0) = q\bigl(x_T \mid x_{T-1}\bigr) \prod_{t=1}^{T-1} q\bigl(x_t \mid x_{t-1}\bigr). q ( x 1 : T ∣ x 0 ) = q ( x T ∣ x T − 1 ) t = 1 ∏ T − 1 q ( x t ∣ x t − 1 ) .
원래 연쇄법칙(chain rule) 으로 p ( x 0 : T ) p(x_{0:T}) p ( x 0 : T ) p ( x 0 ) ∏ t = 1 T p ( x t ∣ x 0 , … , x t − 1 ) \displaystyle p(x_0)\prod_{t=1}^T p(x_t \mid x_0,\dots, x_{t-1}) p ( x 0 ) t = 1 ∏ T p ( x t ∣ x 0 , … , x t − 1 )
그런데 여기서는 모델이 “역방향”으로 조건을 거는 형태 (x t ∣ x t + 1 x_t \mid x_{t+1} x t ∣ x t + 1
이건 “Hidden Markov Model”을 뒤집어서 본다든지, “backward RNN” 같은 걸 떠올리시면 됩니다.
즉, “x t + 1 x_{t+1} x t + 1 x t x_t x t
분모 역시, 우리가 설정한 변분분포 q q q Markov 구조 를 가정해서
q ( x 1 : T ∣ x 0 ) = ∏ t = 1 T q ( x t ∣ x t − 1 ) , q(x_{1:T}\mid x_0) \;=\; \prod_{t=1}^T q\bigl(x_t \mid x_{t-1}\bigr), q ( x 1 : T ∣ x 0 ) = t = 1 ∏ T q ( x t ∣ x t − 1 ) , (단, x − 1 ≡ x 0 x_{-1}\equiv x_0 x − 1 ≡ x 0
3. log ( p q ) \log(\frac{p}{q}) log ( q p ) 각 항별로 묶어서 쓰기
위처럼 분자를
p ( x T ) p θ ( x 0 ∣ x 1 ) ∏ t = 1 T − 1 p θ ( x t ∣ x t + 1 ) , p(x_T)\,p_\theta\bigl(x_0 \mid x_1\bigr)\,\prod_{t=1}^{T-1}p_\theta\bigl(x_t \mid x_{t+1}\bigr), p ( x T ) p θ ( x 0 ∣ x 1 ) t = 1 ∏ T − 1 p θ ( x t ∣ x t + 1 ) , 분모를
q ( x T ∣ x T − 1 ) ∏ t = 1 T − 1 q ( x t ∣ x t − 1 ) , q\bigl(x_T \mid x_{T-1}\bigr)\,\prod_{t=1}^{T-1} q\bigl(x_t \mid x_{t-1}\bigr), q ( x T ∣ x T − 1 ) t = 1 ∏ T − 1 q ( x t ∣ x t − 1 ) , 로 써놓고, log ( p q ) \log\bigl(\frac{p}{q}\bigr) log ( q p )
log ( p ( x 0 : T ) q ( x 1 : T ∣ x 0 ) ) = log ( p ( x T ) p θ ( x 0 ∣ x 1 ) ∏ t = 1 T − 1 p θ ( x t ∣ x t + 1 ) q ( x T ∣ x T − 1 ) ∏ t = 1 T − 1 q ( x t ∣ x t − 1 ) ) . \log\Bigl(\frac{p(x_{0:T})}{q(x_{1:T}\mid x_0)}\Bigr) = \log\left( \frac{p(x_T)\,p_\theta(x_0 \mid x_1)\,\prod_{t=1}^{T-1} p_\theta(x_t \mid x_{t+1})} {q(x_T \mid x_{T-1})\,\prod_{t=1}^{T-1} q(x_t \mid x_{t-1})} \right). log ( q ( x 1 : T ∣ x 0 ) p ( x 0 : T ) ) = log ( q ( x T ∣ x T − 1 ) ∏ t = 1 T − 1 q ( x t ∣ x t − 1 ) p ( x T ) p θ ( x 0 ∣ x 1 ) ∏ t = 1 T − 1 p θ ( x t ∣ x t + 1 ) ) . 즉,
= log ( p ( x T ) ) + log ( p θ ( x 0 ∣ x 1 ) ) + ∑ t = 1 T − 1 log ( p θ ( x t ∣ x t + 1 ) ) − ( log ( q ( x T ∣ x T − 1 ) ) + ∑ t = 1 T − 1 log ( q ( x t ∣ x t − 1 ) ) ) . = \log\Bigl(p(x_T)\Bigr) + \log\Bigl(p_\theta(x_0 \mid x_1)\Bigr) + \sum_{t=1}^{T-1}\log\Bigl(p_\theta(x_t \mid x_{t+1})\Bigr) \;-\; \Bigl( \log\bigl(q(x_T \mid x_{T-1})\bigr) + \sum_{t=1}^{T-1}\log\bigl(q(x_t \mid x_{t-1})\bigr) \Bigr). = log ( p ( x T ) ) + log ( p θ ( x 0 ∣ x 1 ) ) + t = 1 ∑ T − 1 log ( p θ ( x t ∣ x t + 1 ) ) − ( log ( q ( x T ∣ x T − 1 ) ) + t = 1 ∑ T − 1 log ( q ( x t ∣ x t − 1 ) ) ) . “로그 분자의 합 – 로그 분모의 합”이 되는 거죠.
그런 다음 필요한 항들을 서로 묶어서
log p θ ( x 0 ∣ x 1 ) \log p_\theta(x_0\mid x_1) log p θ ( x 0 ∣ x 1 ) p ( x T ) p(x_T) p ( x T ) q ( x T ∣ x T − 1 ) q(x_T\mid x_{T-1}) q ( x T ∣ x T − 1 ) p θ ( x t ∣ x t + 1 ) p_\theta(x_t\mid x_{t+1}) p θ ( x t ∣ x t + 1 ) q ( x t ∣ x t − 1 , x t + 1 ) q(x_t\mid x_{t-1}, x_{t+1}) q ( x t ∣ x t − 1 , x t + 1 )
이런 식으로 정리해서 KL 발산 + 로그우도 형태로 재배열하는 겁니다.
4. 최종적으로 “3개 항”이 나오는 이유
위에서 말한 “묶기”를 살짝 수학적으로 해 보면,
(1) 재구성 항 :E q ( x 1 ∣ x 0 ) [ log p θ ( x 0 ∣ x 1 ) ] \mathbb{E}_{q(x_1\mid x_0)}[\log p_\theta(x_0\mid x_1)] E q ( x 1 ∣ x 0 ) [ log p θ ( x 0 ∣ x 1 ) ] x 1 x_1 x 1 x 0 x_0 x 0
(2) Prior matching :− E q ( x T − 1 ∣ x 0 ) [ K L ( q ( x T ∣ x T − 1 ) ∥ p ( x T ) ) ] - \mathbb{E}_{q(x_{T-1}\mid x_0)}[\mathrm{KL}(\,q(x_T\mid x_{T-1})\|\;p(x_T)\,)] − E q ( x T − 1 ∣ x 0 ) [ K L ( q ( x T ∣ x T − 1 ) ∥ p ( x T ) ) ] p ( x T ) p(x_T) p ( x T )
(3) Consistency(시간적 일관성) :− ∑ t = 1 T − 1 E q ( x t − 1 , x t + 1 ∣ x 0 ) [ K L ( q ( x t ∣ x t − 1 , x t + 1 ) ∥ p θ ( x t ∣ x t + 1 ) ) ] - \sum_{t=1}^{T-1} \mathbb{E}_{q(x_{t-1}, x_{t+1}\mid x_0)}[\mathrm{KL}(\,q(x_t\mid x_{t-1},x_{t+1})\|\;p_\theta(x_t\mid x_{t+1})\,)] − ∑ t = 1 T − 1 E q ( x t − 1 , x t + 1 ∣ x 0 ) [ K L ( q ( x t ∣ x t − 1 , x t + 1 ) ∥ p θ ( x t ∣ x t + 1 ) ) ] x t x_t x t
즉,x 0 x_0 x 0
이렇게 정리되면서 3가지 항이 나옵니다.(우도) − (KL) \text{(우도)} - \text{(KL)} ( 우도 ) − (KL) 시계열 구조 가 들어가서 KL 항이 여러 개로 나뉜다고 보시면 됩니다.
5. 직관적으로 보면…
우리는 log p ( x 0 ) \log p(x_0) log p ( x 0 ) , 직접 계산하기 어려움. 그래서 “변분분포 q ( x 1 : T ∣ x 0 ) q(x_{1:T}\mid x_0) q ( x 1 : T ∣ x 0 ) log p ( x 0 ) ≥ E q [ log ( p / q ) ] = E q [ log p ] − E q [ log q ] . \log p(x_0) \ge \mathbb{E}_{q}[\log (p/q)] = \mathbb{E}_{q}[\log p] - \mathbb{E}_{q}[\log q]. log p ( x 0 ) ≥ E q [ log ( p / q ) ] = E q [ log p ] − E q [ log q ] .
위에서 log p \log p log p log q \log q log q
“log p θ ( x 0 ∣ x 1 ) \log p_\theta(x_0\mid x_1) log p θ ( x 0 ∣ x 1 ) 재구성 항 ,
“KL( (q) || (p) )” 형태의 규제(regulation) 항
결국 이걸 전부 합쳐서 최대화 해주면,
(1) 데이터 재구성도 잘 되면서,
(2) 시계열 잠재변수들도 모델이 원하는 구조/분포에 맞춰서 정렬(alignment)되도록 학습
6. 요약
분수 p q \frac{p}{q} q p 해서 로그 를 취하면, (로그 분자) – (로그 분모) 항들이 주루룩 나옴. 그 항들을 어떻게 묶어주느냐 에 따라,
재구성(likelihood) 항
Prior와의 KL 항
중간 시점들 간의 KL 항(시간적 일관성)
이 3개 묶음 이 바로 식에서 보이는 형태입니다.
전반적인 구조는 VAE가 (재구성 우도) − (KL 발산) \text{(재구성 우도)} - \text{(KL 발산)} ( 재구성 우도 ) − (KL 발산 ) 시계열 특성 때문에 KL 항이 여러 개(끝 시점, 중간 시점들 등)로 세분화된다고 보면 이해하기 쉽습니다.
따라서 복잡해 보이지만, 결국은
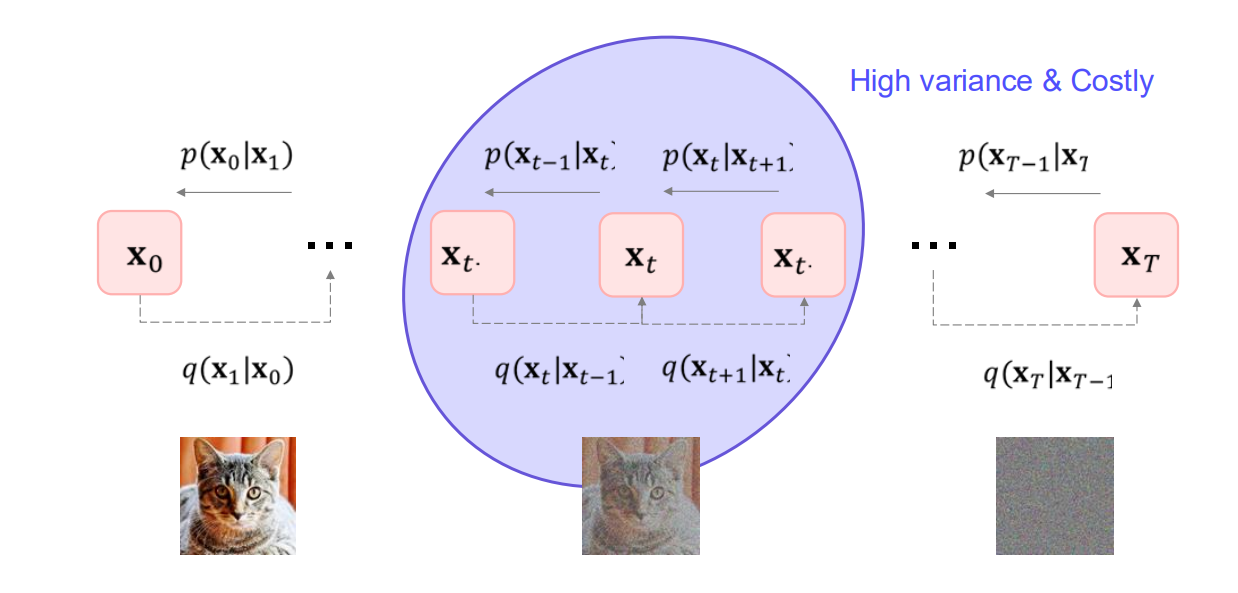
“log p ( x ) \log p(x) log p ( x ) 4. 그림을 통한 이해
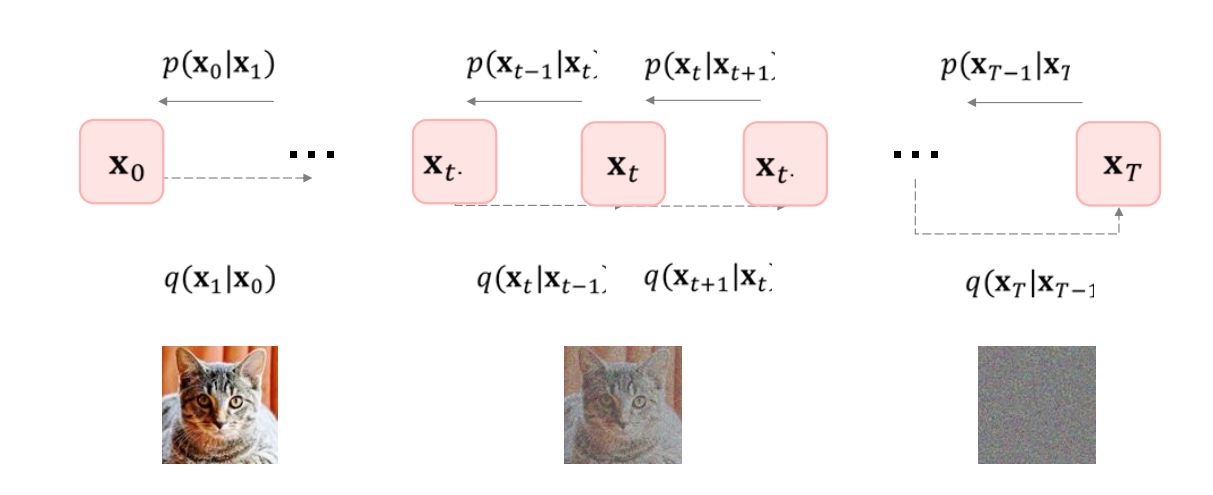
x 0 x_0 x 0 x 1 , x 2 , … , x T x_1, x_2, \dots, x_T x 1 , x 2 , … , x T 노이즈가 추가된 이미지 . 전방(Forward) 과정 q ( x t + 1 ∣ x t ) q(x_{t+1}\mid x_t) q ( x t + 1 ∣ x t ) p ( x t ∣ x t + 1 ) p(x_t\mid x_{t+1}) p ( x t ∣ x t + 1 )
최종 x T x_T x T 순수한 노이즈 상태가 되면, 역방향으로 노이즈를 제거하며 x 0 x_0 x 0
요약
log p ( x ) \log p(x) log p ( x )
중간 스텝 x 1 : T x_{1:T} x 1 : T
q ( x 1 : T ∣ x 0 ) q(x_{1:T}\mid x_0) q ( x 1 : T ∣ x 0 )
적분을 기댓값 형태로 바꾸고, Jensen 부등식을 통해 ELBO를 얻음.
ELBO 항 해석
Likelihood( x 0 x_0 x 0
KL 항(모델 분포 vs. 보조 분포 일치),
Consistency(시간 스텝 간 정합성) 등.
Diffusion Model 맥락
전방 과정: 이미지에 노이즈 첨가
역방향 과정: 노이즈 제거(디노이징)
ELBO 최대화로, 실제 이미지를 잘 복원(생성)하는 디노이징 과정을 학습
위와 같이 VDM 에서도 다른 VA류 모델처럼, log p ( x ) \log p(x) log p ( x )
(3). ELBO: 2nd try(한 번에 한 개의 랜덤 변수에 대해 기댓값을 계산하기)
이번에는 ELBO 를 유도하는 과정에서, 각 항을 한 번에 한 개의 랜덤 변수 에 대한 기댓값 형태로 재구성해봅시다.
1. 문제 설정
원래는 q ( x t ∣ x t − 1 ) q(x_t \mid x_{t-1}) q ( x t ∣ x t − 1 ) x 0 x_0 x 0
그래서 q ( x t ∣ x t − 1 , x 0 ) q(x_t \mid x_{t-1}, x_0) q ( x t ∣ x t − 1 , x 0 ) x t x_t x t x t − 1 x_{t-1} x t − 1 x 0 x_0 x 0
핵심 아이디어(Key Insight)
Bayes' Rule 를 사용하여,q ( x t ∣ x t − 1 , x 0 ) = q ( x t − 1 ∣ x t , x 0 ) q ( x t ∣ x 0 ) q ( x t − 1 ∣ x 0 ) . q(x_t \mid x_{t-1}, x_0) \;=\; \frac{q(x_{t-1}\mid x_t, x_0)\,q(x_t\mid x_0)}{q(x_{t-1}\mid x_0)}. q ( x t ∣ x t − 1 , x 0 ) = q ( x t − 1 ∣ x 0 ) q ( x t − 1 ∣ x t , x 0 ) q ( x t ∣ x 0 ) . 이렇게 분해해두면, 나중에 적분(합)을 기댓값 형태로 바꾸고 나서, 한 스텝씩 기댓값을 정의하는 데 도움이 됩니다.
2. ELBO 식 다시 살펴보기
첫 번째 모습
log p ( x ) ≥ E q ( x 1 : T ∣ x 0 ) [ log ( p ( x 0 : T ) q ( x 1 : T ∣ x 0 ) ) ] . \log p(x) \;\ge\; E_{q(x_{1:T}\mid x_0)} \Bigl[ \log \bigl( \frac{p(x_{0:T})}{q(x_{1:T}\mid x_0)} \bigr) \Bigr]. log p ( x ) ≥ E q ( x 1 : T ∣ x 0 ) [ log ( q ( x 1 : T ∣ x 0 ) p ( x 0 : T ) ) ] .
분해
p ( x 0 : T ) p(x_{0:T}) p ( x 0 : T ) p ( x T ) p ( x T − 1 ∣ x T ) … p ( x 0 ∣ x 1 ) p(x_T)\,p(x_{T-1}\mid x_T)\,\dots\,p(x_0\mid x_1) p ( x T ) p ( x T − 1 ∣ x T ) … p ( x 0 ∣ x 1 ) q ( x 1 : T ∣ x 0 ) = ∏ t = 1 T q ( x t ∣ x t − 1 , x 0 ) q(x_{1:T}\mid x_0) = \prod_{t=1}^T q(x_t \mid x_{t-1}, x_0) q ( x 1 : T ∣ x 0 ) = ∏ t = 1 T q ( x t ∣ x t − 1 , x 0 ) 각 항을 로그 안에 모아두면,log ( p ( x 0 : T ) q ( x 1 : T ∣ x 0 ) ) = log p ( x T ) + log p ( x T − 1 ∣ x T ) + ⋯ + log p ( x 0 ∣ x 1 ) − ∑ t = 1 T log q ( x t ∣ x t − 1 , x 0 ) . \log \bigl( \frac{p(x_{0:T})}{q(x_{1:T}\mid x_0)} \bigr) = \log p(x_T) + \log p(x_{T-1}\mid x_T) + \dots + \log p(x_0\mid x_1) \;-\; \sum_{t=1}^T \log q(x_t \mid x_{t-1}, x_0). log ( q ( x 1 : T ∣ x 0 ) p ( x 0 : T ) ) = log p ( x T ) + log p ( x T − 1 ∣ x T ) + ⋯ + log p ( x 0 ∣ x 1 ) − t = 1 ∑ T log q ( x t ∣ x t − 1 , x 0 ) .
한 스텝씩 기댓값
위 항들을 묶어보면, 한 스텝(x t x_t x t
E q ( x 1 : T ∣ x 0 ) [ ⋯ ] E_{q(x_{1:T}\mid x_0)}[\cdots] E q ( x 1 : T ∣ x 0 ) [ ⋯ ] t = 1 t=1 t = 1 T T T
3. 결과적으로 얻는 ELBO 형태
아래와 같은 꼴로 나타낼 수 있게 됩니다:
Likelihood(재구성 항)
E q ( x 1 ∣ x 0 ) [ log p θ ( x 0 ∣ x 1 ) ] E_{q(x_1\mid x_0)} [\,\log p_\theta(x_0\mid x_1)\,] E q ( x 1 ∣ x 0 ) [ log p θ ( x 0 ∣ x 1 ) ] "최종적으로 x 0 x_0 x 0
Prior matching
− K L ( q ( x T ∣ x 0 ) ∥ p ( x T ) ) -\,KL\bigl(q(x_T\mid x_0)\,\|\;p(x_T)\bigr) − K L ( q ( x T ∣ x 0 ) ∥ p ( x T ) ) 맨 끝 상태($ x_T $)가 사전에 정한 분포(예: 노이즈)와 일치하도록.
Denoising matching
− ∑ t = 2 T E q ( x t , x t + 1 ∣ x 0 ) [ K L ( q ( x t − 1 ∣ x t , x 0 ) ∥ p θ ( x t − 1 ∣ x t ) ) ] -\,\sum_{t=2}^T E_{q(x_t,x_{t+1}\mid x_0)} \bigl[ KL\bigl(q(x_{t-1}\mid x_t,x_0)\,\|\;p_\theta(x_{t-1}\mid x_t)\bigr) \bigr] − ∑ t = 2 T E q ( x t , x t + 1 ∣ x 0 ) [ K L ( q ( x t − 1 ∣ x t , x 0 ) ∥ p θ ( x t − 1 ∣ x t ) ) ] 각 단계에서 "디노이징" 역방향 분포가 잘 맞도록 하는 항.
아래 수식은, 어떤 확률 모델 (p(x))에 대해 변분(variational) 방법을 이용해 로그가능도 (\log p(x))를 하한(lower bound)으로 표현한 식입니다. 흔히 VAE(Variational AutoEncoder)나 그 변형 모델에서 자주 보게 되는 형태이며, 시계열 데이터를 다룰 때(또는 순서가 있는 데이터를 다룰 때) 쓰이는 특수한 버전이라 볼 수 있습니다.
Likelihood, prior Matching, Denoising matching에 대해서 자세하게 풀어써보자.
식의 형태
우선 식을 단계적으로 살펴봅시다. 맨 위 식은 다음과 같습니다.
log p ( x ) ≥ E q ( x 1 : T ∣ x 0 ) [ log ( p ( x 0 : T ) q ( x 1 : T ∣ x 0 ) ) ] . \log p(x) \;\;\ge\;\; \mathbb{E}_{q(x_{1:T}\mid x_0)}\!\Bigl[\log\Bigl(\frac{p(x_{0:T})}{q(x_{1:T}\mid x_0)}\Bigr)\Bigr]. log p ( x ) ≥ E q ( x 1 : T ∣ x 0 ) [ log ( q ( x 1 : T ∣ x 0 ) p ( x 0 : T ) ) ] .
x 0 x_0 x 0 관측 데이터 (혹은 조건으로 주어진 변수)라고 생각할 수 있습니다. x 1 : T = ( x 1 , x 2 , … , x T ) x_{1:T} = (x_1, x_2, \dots, x_T) x 1 : T = ( x 1 , x 2 , … , x T ) 잠재(혹은 숨겨진) 시퀀스 입니다. q ( x 1 : T ∣ x 0 ) q(x_{1:T}\mid x_0) q ( x 1 : T ∣ x 0 ) 변분 분포 (variational distribution)로, 실제 우리가 다루기 어려운 p ( x 1 : T ∣ x 0 ) p(x_{1:T}\mid x_0) p ( x 1 : T ∣ x 0 )
이 식은 변분 부등식(ELBO, Evidence Lower BOund)의 전형적인 형태로,
log p ( x ) ≥ E q [ log p − log q ] . \log p(x) \;\;\ge\;\; \mathbb{E}_{q}[\log p - \log q]. log p ( x ) ≥ E q [ log p − log q ] . 분자·분모 확장
그 다음 단계에서 분자 p ( x 0 : T ) \;p(x_{0:T}) p ( x 0 : T ) q ( x 1 : T ∣ x 0 ) \;q(x_{1:T} \mid x_0) q ( x 1 : T ∣ x 0 )
p ( x 0 : T ) = p ( x T ) p θ ( x 0 ∣ x 1 ) ∏ t = 1 T − 1 p θ ( x t ∣ x t + 1 ) , p(x_{0:T}) \;=\; p(x_T)\,p_\theta(x_0 \mid x_1)\,\prod_{t=1}^{T-1}p_\theta(x_t \mid x_{t+1}), p ( x 0 : T ) = p ( x T ) p θ ( x 0 ∣ x 1 ) t = 1 ∏ T − 1 p θ ( x t ∣ x t + 1 ) , q ( x 1 : T ∣ x 0 ) = q ( x T ∣ x T − 1 ) ∏ t = 1 T − 1 q ( x t ∣ x t − 1 ) . q(x_{1:T} \mid x_0) \;=\; q(x_T \mid x_{T-1}) \,\prod_{t=1}^{T-1} q(x_t \mid x_{t-1}). q ( x 1 : T ∣ x 0 ) = q ( x T ∣ x T − 1 ) t = 1 ∏ T − 1 q ( x t ∣ x t − 1 ) . 이를 식에 대입하면,
log ( p ( x 0 : T ) q ( x 1 : T ∣ x 0 ) ) = log ( p ( x T ) p θ ( x 0 ∣ x 1 ) ∏ t = 1 T − 1 p θ ( x t ∣ x t + 1 ) q ( x T ∣ x T − 1 ) ∏ t = 1 T − 1 q ( x t ∣ x t − 1 ) ) . \log \left(\frac{p(x_{0:T})}{q(x_{1:T}\mid x_0)}\right) \;=\; \log\left( \frac{ p(x_T)\,p_\theta(x_0 \mid x_1)\,\prod_{t=1}^{T-1} p_\theta(x_t \mid x_{t+1}) }{ q(x_T \mid x_{T-1}) \,\prod_{t=1}^{T-1} q(x_t \mid x_{t-1}) } \right). log ( q ( x 1 : T ∣ x 0 ) p ( x 0 : T ) ) = log ( q ( x T ∣ x T − 1 ) ∏ t = 1 T − 1 q ( x t ∣ x t − 1 ) p ( x T ) p θ ( x 0 ∣ x 1 ) ∏ t = 1 T − 1 p θ ( x t ∣ x t + 1 ) ) . 항의 묶음
이 식은 적절히 묶어서 세 가지 항으로 나눌 수 있습니다. 실제 식에서는,
E q ( x 1 : T ∣ x 0 ) [ log p θ ( x 0 ∣ x 1 ) ] − E q ( x T − 1 ∣ x 0 ) [ K L ( q ( x T ∣ x T − 1 ) ∥ p ( x T ) ) ] − ∑ t = 1 T − 1 E q ( x t − 1 , x t + 1 ∣ x 0 ) [ K L ( q ( x t ∣ x t − 1 , x t + 1 ) ∥ p θ ( x t ∣ x t + 1 ) ) ] . \begin{aligned} \mathbb{E}_{q(x_{1:T}\mid x_0)} \Bigl[ \log p_\theta(x_0 \mid x_1) \Bigr] &-\; \mathbb{E}_{q(x_{T-1}\mid x_0)} \Bigl[ \mathrm{KL}\bigl(q(x_T\mid x_{T-1}) \,\|\, p(x_T)\bigr) \Bigr]\\ &-\; \sum_{t=1}^{T-1} \mathbb{E}_{q(x_{t-1},x_{t+1}\mid x_0)} \Bigl[ \mathrm{KL}\bigl(q(x_t \mid x_{t-1}, x_{t+1}) \,\|\, p_\theta(x_t \mid x_{t+1})\bigr) \Bigr]. \end{aligned} E q ( x 1 : T ∣ x 0 ) [ log p θ ( x 0 ∣ x 1 ) ] − E q ( x T − 1 ∣ x 0 ) [ K L ( q ( x T ∣ x T − 1 ) ∥ p ( x T ) ) ] − t = 1 ∑ T − 1 E q ( x t − 1 , x t + 1 ∣ x 0 ) [ K L ( q ( x t ∣ x t − 1 , x t + 1 ) ∥ p θ ( x t ∣ x t + 1 ) ) ] . 이렇게 정리됩니다. 식에 달려 있는 주석을 보면 각각 다음과 같이 해석이 붙어 있습니다.
Likelihood (reconstruction) 항
E q ( x 1 ∣ x 0 ) [ log p θ ( x 0 ∣ x 1 ) ] \mathbb{E}_{q(x_1 \mid x_0)} \bigl[\log p_\theta(x_0 \mid x_1)\bigr] E q ( x 1 ∣ x 0 ) [ log p θ ( x 0 ∣ x 1 ) ]
모델이 잠재표현 x 1 x_1 x 1 x 0 x_0 x 0 재구성(reconstruct) 하는지 나타내는 항입니다.
VAE에서 흔히 log p θ ( x ∣ z ) \log p_\theta(x \mid z) log p θ ( x ∣ z )
Prior matching 항
− E q ( x T − 1 ∣ x 0 ) [ K L ( q ( x T ∣ x T − 1 ) ∥ p ( x T ) ) ] -\,\mathbb{E}_{q(x_{T-1}\mid x_0)} \Bigl[ \mathrm{KL}\bigl(q(x_T\mid x_{T-1}) \,\|\, p(x_T)\bigr) \Bigr] − E q ( x T − 1 ∣ x 0 ) [ K L ( q ( x T ∣ x T − 1 ) ∥ p ( x T ) ) ]
뒤쪽 시점 x T x_T x T 사전분포(prior) p ( x T ) p(x_T) p ( x T ) q ( x T ∣ x T − 1 ) q(x_T \mid x_{T-1}) q ( x T ∣ x T − 1 )
즉, K L \mathrm{KL} K L q q q p p p
Consistency 항
− ∑ t = 1 T − 1 E q ( x t − 1 , x t + 1 ∣ x 0 ) [ K L ( q ( x t ∣ x t − 1 , x t + 1 ) ∥ p θ ( x t ∣ x t + 1 ) ) ] . -\,\sum_{t=1}^{T-1} \mathbb{E}_{q(x_{t-1},x_{t+1}\mid x_0)} \Bigl[ \mathrm{KL}\bigl(q(x_t \mid x_{t-1}, x_{t+1}) \,\|\, p_\theta(x_t \mid x_{t+1})\bigr) \Bigr]. − t = 1 ∑ T − 1 E q ( x t − 1 , x t + 1 ∣ x 0 ) [ K L ( q ( x t ∣ x t − 1 , x t + 1 ) ∥ p θ ( x t ∣ x t + 1 ) ) ] .
중간 시점들 t = 1 , … , T − 1 t=1,\dots,T-1 t = 1 , … , T − 1 앞 시점 (x t − 1 x_{t-1} x t − 1 뒤 시점 (x t + 1 x_{t+1} x t + 1 q ( x t ∣ x t − 1 , x t + 1 q(x_t\mid x_{t-1}, x_{t+1} q ( x t ∣ x t − 1 , x t + 1 p θ ( x t ∣ x t + 1 ) p_\theta(x_t \mid x_{t+1}) p θ ( x t ∣ x t + 1 )
이를 통해 시계열(혹은 순차) 구조에서 시간축 양방향 정보를 조화롭게 맞추어 주는 “일관성(consistency)”을 구현합니다.
전체적인 의미
log p ( x ) \log p(x) log p ( x ) log p ( x ) \log p(x) log p ( x ) q q q
log p ( x ) ≥ E q [ log p − log q ] \log p(x) \;\;\ge\;\; \mathbb{E}_{q} [\log p - \log q] log p ( x ) ≥ E q [ log p − log q ] 형태로 우변(ELBO)을 최대화함으로써 log p ( x ) \log p(x) log p ( x )
재구성 + 정규화(prior, consistency) 항 :
재구성(likelihood) : 잠재변수로부터 원본 x 0 x_0 x 0 사전분포와 정합 : 끝 시점(T 시점)의 분포가 사전에 맞도록(regularization) 중간 단계들의 일관성 : 시계열 구조 상에서 변분분포와 모델의 조건부분포가 일치하도록
이 세 가지를 같이 최적화함으로써, 모델이 시계열 구조 와 관측 데이터를 재구성하는 능력 을 동시에 학습하게 됩니다.
정리
위 식은 시계열(또는 순서가 있는 잠재변수 구조)을 갖춘 변분 오토인코더류 모델에서 자주 볼 수 있는 변분 하한(ELBO)의 확장판입니다.
첫 번째 항(재구성)은 “입력을 주고 잠재변수를 통해 다시 입력을 복원했을 때 정확도” 를 높이는 방향으로 작용하고,
두 번째·세 번째 항은 “잠재변수 분포가 사전분포와 어떻게 일치해야 하고, 시계열 구조에서 어떻게 일관성을 유지해야 하는지” 를 KL 발산 형태로 강제하여 모델을 정규화(regularize)합니다.
이런 방식을 통해 모델은 자료의 시계열적 특성 을 내적으로 학습하여, 보이지 않는 부분에 대해서도 자연스럽게 샘플링하거나, 추론할 수 있게 됩니다. 요약하면,
ELBO = (재구성 항) – (KL 발산 항들의 합) 각 KL 발산 항은 모델의 prior 및 조건부 구조와 변분분포를 가깝게 만든다 이를 통해 데이터를 잘 복원 하면서도, 잠재변수의 시계열 구조 를 잘 맞춰주는 학습이 가능해진다
라는 점이 핵심입니다.
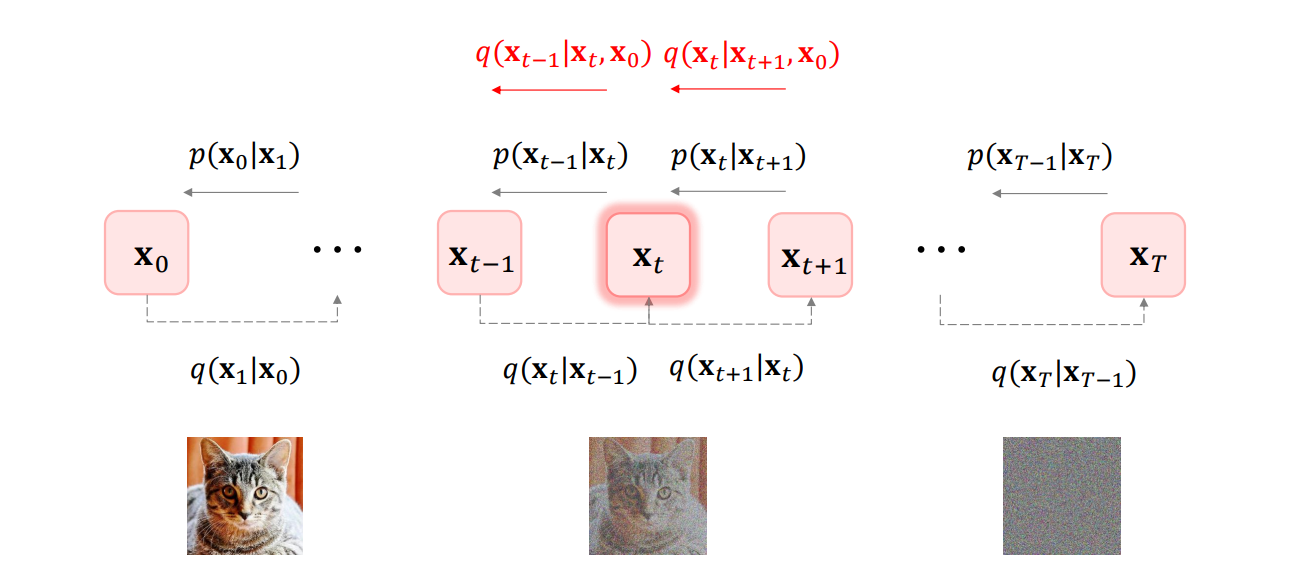
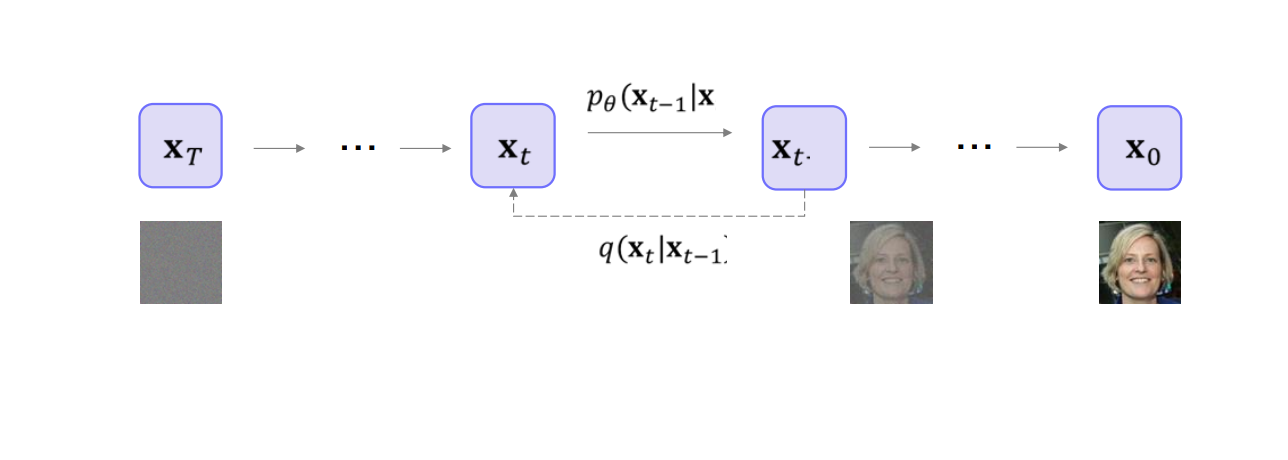
4. 그림 설명
x 0 x_0 x 0 x 1 , … , x T − 1 , x T x_1,\dots,x_{T-1}, x_T x 1 , … , x T − 1 , x T q ( x t ∣ x t − 1 , x 0 ) q(x_t\mid x_{t-1},x_0) q ( x t ∣ x t − 1 , x 0 ) p θ ( x t − 1 ∣ x t ) p_\theta(x_{t-1}\mid x_t) p θ ( x t − 1 ∣ x t ) 한 번에 하나의 x t x_t x t 기댓값 을 따로 구해서 전체를 합치면, ELBO를 간단히 표현할 수 있습니다.
요약
q ( x t ∣ x t − 1 , x 0 ) q(x_t \mid x_{t-1},x_0) q ( x t ∣ x t − 1 , x 0 )
각 스텝 x t x_t x t x t − 1 x_{t-1} x t − 1 x 0 x_0 x 0
Bayes' Rule 로 분해
q ( x t − 1 ∣ x t , x 0 ) = q ( x t − 1 ∣ x 0 ) q ( x t ∣ x 0 ) q ( x t ∣ x 0 ) q(x_{t-1}\mid x_t,x_0) = \frac{q(x_{t-1}\mid x_0)\,q(x_t\mid x_0)}{q(x_t\mid x_0)} q ( x t − 1 ∣ x t , x 0 ) = q ( x t ∣ x 0 ) q ( x t − 1 ∣ x 0 ) q ( x t ∣ x 0 ) 이를 활용해 기댓값 계산 시 한 스텝씩 나누어 다룸.
ELBO 결과
(Likelihood) + (Prior matching) + (Denoising matching) 형태로 항들이 깔끔히 정리됨.
모델이 p θ ( x t − 1 ∣ x t ) p_\theta(x_{t-1}\mid x_t) p θ ( x t − 1 ∣ x t )
이 과정을 통해, ELBO를 좀 더 단계별로 나누어 살펴볼 수 있고, 각 항을 단 하나의 랜덤 변수 에 대한 기댓값으로 계산함으로써 변동성(분산)을 줄이고 학습을 용이하게 만들 수 있습니다.
3. Other equivalent parameterizations
3.1 Other equivalent parameterizations: ver. 2
본 내용은 확산 모델(Diffusion Model)에서 다른 형태의(Equivalent) 파라미터화가 어떻게 유도되는지를 단계적으로 보여줍니다.결론 부터 말하자면, 우리가 Reverse Process 의 분포를 모델링할 때,x 0 x_0 x 0 ϵ 0 \epsilon_0 ϵ 0 서로 동치 임을 증명하고 있습니다.
1. 기본 식: x t x_t x t x 0 x_0 x 0 ϵ 0 \epsilon_0 ϵ 0
일반적으로 DDPM(Denoising Diffusion Probabilistic Model)에서,t t t x t x_t x t 노이즈 추가 로 표현할 수 있습니다.
x t = α ‾ t x 0 + 1 − α ‾ t ϵ 0 , x_t = \sqrt{\overline{\alpha}_t}\,x_0 + \sqrt{\,1 - \overline{\alpha}_t\,}\,\epsilon_0, x t = α t x 0 + 1 − α t ϵ 0 ,
여기서 α ‾ t \overline{\alpha}_t α t α 1 ⋯ α t \alpha_1 \cdots \alpha_t α 1 ⋯ α t
ϵ 0 \epsilon_0 ϵ 0 x 0 x_0 x 0
2. x 0 x_0 x 0 x t x_t x t ϵ 0 \epsilon_0 ϵ 0
위 식을 재배열 하면, x 0 x_0 x 0
x 0 = x t − 1 − α ‾ t ϵ 0 α ‾ t . x_0 = \frac{\,x_t - \sqrt{\,1 - \overline{\alpha}_t\,}\,\epsilon_0\,}{\sqrt{\,\overline{\alpha}_t\,}}. x 0 = α t x t − 1 − α t ϵ 0 . 이 식은 “주어진 x t x_t x t ϵ 0 \epsilon_0 ϵ 0 x 0 x_0 x 0 ”를 보여줍니다.
3. μ q ( x t , x 0 ) \mu_q(x_t, x_0) μ q ( x t , x 0 )
Reverse Process에서, 시점 t t t t − 1 t-1 t − 1 q ( x t − 1 ∣ x t , x 0 ) q(x_{t-1} \mid x_t, x_0) q ( x t − 1 ∣ x t , x 0 ) 평균 (Mean) 항을 μ q ( x t , x 0 ) \mu_q(x_t, x_0) μ q ( x t , x 0 ) μ q \mu_q μ q
μ q ( x t , x 0 ) = α ‾ t ( 1 − α ‾ t − 1 ) x t + α ‾ t − 1 ( 1 − α t ) x 0 1 − α ‾ t . \mu_q(x_t, x_0) = \frac{ \sqrt{\overline{\alpha}_t\,(1 - \overline{\alpha}_{t-1})}\,x_t \;+\; \sqrt{\overline{\alpha}_{t-1}\,(1 - \alpha_t)}\,x_0 }{ 1 - \overline{\alpha}_t }. μ q ( x t , x 0 ) = 1 − α t α t ( 1 − α t − 1 ) x t + α t − 1 ( 1 − α t ) x 0 . 이제 위에서 구한 x 0 x_0 x 0 x 0 = x t − 1 − α ‾ t ϵ 0 α ‾ t x_0 = \frac{x_t - \sqrt{1 - \overline{\alpha}_t}\,\epsilon_0}{\sqrt{\overline{\alpha}_t}} x 0 = α t x t − 1 − α t ϵ 0
μ q ( x t , x 0 ) = α ‾ t ( 1 − α ‾ t − 1 ) x t + α ‾ t − 1 ( 1 − α t ) ( x t − 1 − α ‾ t ϵ 0 α ‾ t ) 1 − α ‾ t . \mu_q(x_t, x_0) = \frac{ \sqrt{\overline{\alpha}_t\,\bigl(1 - \overline{\alpha}_{t-1}\bigr)}\,x_t \;+\; \sqrt{\,\overline{\alpha}_{t-1}\,\bigl(1 - \alpha_t\bigr)}\, \Bigl(\!\frac{x_t - \sqrt{\,1 - \overline{\alpha}_t\,}\,\epsilon_0}{\sqrt{\overline{\alpha}_t}} \Bigr) }{ 1 - \overline{\alpha}_t }. μ q ( x t , x 0 ) = 1 − α t α t ( 1 − α t − 1 ) x t + α t − 1 ( 1 − α t ) ( α t x t − 1 − α t ϵ 0 ) . 이를 간단히 정리하면 다음처럼 됩니다.
μ q ( x t , x 0 ) = 1 α ‾ t x t − 1 − α t 1 − α ‾ t α ‾ t ϵ 0 . \mu_q(x_t, x_0) = \frac{1}{\sqrt{\overline{\alpha}_t}}\;x_t \;-\; \frac{\,1 - \alpha_t\,}{\sqrt{\,1 - \overline{\alpha}_t\,}\,\sqrt{\overline{\alpha}_t}}\,\epsilon_0. μ q ( x t , x 0 ) = α t 1 x t − 1 − α t α t 1 − α t ϵ 0 . 결국 μ q ( x t , x 0 ) \mu_q(x_t, x_0) μ q ( x t , x 0 ) x t x_t x t ϵ 0 \epsilon_0 ϵ 0
4. KL 발산 최소화 & 파라미터화
DDPM에서 Reverse Process를 근사하기 위해, θ \theta θ μ θ \mu_\theta μ θ ϵ θ \epsilon_\theta ϵ θ p θ ( x t − 1 ∣ x t ) ≈ N ( x t − 1 ; μ θ ( x t , t ) , Σ q ( t ) ) . p_\theta(x_{t-1} \mid x_t) \approx \mathcal{N}\!\bigl(x_{t-1};\,\mu_\theta(x_t, t),\,\Sigma_q(t)\bigr). p θ ( x t − 1 ∣ x t ) ≈ N ( x t − 1 ; μ θ ( x t , t ) , Σ q ( t ) ) .
이를 정확한 정규분포 N ( μ q , Σ q ( t ) ) \mathcal{N}\!\bigl(\mu_q, \Sigma_q(t)\bigr) N ( μ q , Σ q ( t ) ) 와 가까워지게 만들려면, 다음 KL 발산을 최소화합니다.
arg min θ K L ( N ( x t − 1 ; μ q , Σ q ( t ) ) ∥ N ( x t − 1 ; μ θ , Σ q ( t ) ) ) . \arg\min_\theta \, KL\!\Bigl( \mathcal{N}\!\bigl(x_{t-1};\,\mu_q,\,\Sigma_q(t)\bigr) \,\big\|\, \mathcal{N}\!\bigl(x_{t-1};\,\mu_\theta,\,\Sigma_q(t)\bigr) \Bigr). arg θ min K L ( N ( x t − 1 ; μ q , Σ q ( t ) ) ∥ ∥ ∥ N ( x t − 1 ; μ θ , Σ q ( t ) ) ) . 이는 평균끼리의 차이에 대한 2차 노름(유클리드 거리)을 최소화하는 문제와 동일해집니다.
= arg min θ 1 2 σ q 2 ( t ) ∥ μ θ ( x t , t ) − μ q ( x t , x 0 ) ∥ 2 2 . = \arg\min_\theta \;\frac{1}{2\,\sigma_q^2(t)}\, \bigl\|\mu_\theta(x_t, t) \;-\; \mu_q(x_t, x_0)\bigr\|_2^2. = arg θ min 2 σ q 2 ( t ) 1 ∥ ∥ ∥ μ θ ( x t , t ) − μ q ( x t , x 0 ) ∥ ∥ ∥ 2 2 . 4.1 x 0 x_0 x 0 ϵ 0 \epsilon_0 ϵ 0
방금 본 식에서,μ q ( x t , x 0 ) \mu_q(x_t, x_0) μ q ( x t , x 0 ) x 0 x_0 x 0 ϵ 0 \epsilon_0 ϵ 0 θ \theta θ
“x 0 x_0 x 0
“ϵ 0 \epsilon_0 ϵ 0
이 과정을 풀어 쓰면,
μ θ ( x t , t ) \mu_\theta(x_t, t) μ θ ( x t , t ) x 0 x_0 x 0 ∥ x ^ θ ( x t , t ) − x 0 ∥ 2 . \|\hat{x}_\theta(x_t, t) - x_0\|^2. ∥ x ^ θ ( x t , t ) − x 0 ∥ 2 .
μ θ ( x t , t ) \mu_\theta(x_t, t) μ θ ( x t , t ) ϵ 0 \epsilon_0 ϵ 0 x 0 x_0 x 0 ϵ 0 \epsilon_0 ϵ 0 ∥ ϵ θ ( x t , t ) − ϵ 0 ∥ 2 \|\epsilon_\theta(x_t, t) - \epsilon_0\|^2 ∥ ϵ θ ( x t , t ) − ϵ 0 ∥ 2
이 두 관점은 서로 등가 이며, 실제 구현 시 노이즈를 예측하는 파라미터화 (ϵ θ \epsilon_\theta ϵ θ
5. 최종 정리
x t = α ‾ t x 0 + 1 − α ‾ t ϵ 0 x_t = \sqrt{\overline{\alpha}_t}\,x_0 + \sqrt{\,1 - \overline{\alpha}_t\,}\,\epsilon_0 x t = α t x 0 + 1 − α t ϵ 0 주어진 x 0 x_0 x 0 표준 노이즈 ϵ 0 \epsilon_0 ϵ 0 노이즈 섞인 샘플 x t x_t x t
이를 재배열하면x 0 = x t − 1 − α ‾ t ϵ 0 α ‾ t . x_0 = \frac{x_t - \sqrt{1 - \overline{\alpha}_t}\,\epsilon_0}{\sqrt{\overline{\alpha}_t}}. x 0 = α t x t − 1 − α t ϵ 0 .
Reverse 분포 q ( x t − 1 ∣ x t , x 0 ) q(x_{t-1} \mid x_t, x_0) q ( x t − 1 ∣ x t , x 0 ) μ q ( x t , x 0 ) \mu_q(x_t, x_0) μ q ( x t , x 0 ) x t , ϵ 0 x_t, \epsilon_0 x t , ϵ 0
μ θ \mu_\theta μ θ μ q \mu_q μ q x 0 x_0 x 0 ϵ 0 \epsilon_0 ϵ 0
“x 0 x_0 x 0 ϵ 0 \epsilon_0 ϵ 0 동등 하며,노이즈 예측 이 더 일반적으로 쓰인다.
이렇게 해서 버전 2의 파라미터화 (= ϵ 0 \epsilon_0 ϵ 0 Other Equivalent Parameterizations 의 핵심 내용입니다.
3.2 Other equivalent parameterizations: ver. 3
이번 버전(ver. 3)에서는 Tweedie's Formula 를 활용하여, Gaussian 변수 의 참된 사후평균 을 추정하는 관점에서 Reverse Process 를 파라미터화하는 방법을 보여줍니다.
가우시안 변수 z ∼ N ( z ; μ z , Σ z ) z \sim \mathcal{N}(z; \mu_z, \Sigma_z) z ∼ N ( z ; μ z , Σ z )
E [ μ z ∣ z ] = z + Σ z ∇ z log p ( z ) . \mathbb{E}[\mu_z \mid z] = z \;+\; \Sigma_z \;\nabla_z\,\log p(z). E [ μ z ∣ z ] = z + Σ z ∇ z log p ( z ) . 이는 z z z 샘플 자체(z z z ” 형태로 표현한다는 점이 핵심입니다.
2. 우리 문제에 적용하기
DDPM 설정에서, x t x_t x t 원본 데이터 x 0 x_0 x 0
q ( x t ∣ x 0 ) = N ( x t ; α ‾ t x 0 , ( 1 − α ‾ t ) I ) . q(x_t \mid x_0) \;=\; \mathcal{N}\!\bigl(x_t; \sqrt{\overline{\alpha}_t}\,x_0,\,(1 - \overline{\alpha}_t)\mathbf{I}\bigr). q ( x t ∣ x 0 ) = N ( x t ; α t x 0 , ( 1 − α t ) I ) .
이에 대응하여, E [ μ x t ∣ x 0 ] \mathbb{E}[\mu_{x_t} \mid x_0] E [ μ x t ∣ x 0 ] 사후평균 을 구해보면
E [ μ x t ∣ x 0 ] = α ‾ t x 0 = x t + ( 1 − α ‾ t ) ∇ x t log p ( x t ) . \mathbb{E}\bigl[\mu_{x_t} \mid x_0\bigr] = \sqrt{\overline{\alpha}_t}\,x_0 \;=\; x_t \;+\; \bigl(1 - \overline{\alpha}_t\bigr)\,\nabla_{x_t}\,\log p(x_t). E [ μ x t ∣ x 0 ] = α t x 0 = x t + ( 1 − α t ) ∇ x t log p ( x t ) . 여기서 마지막 식에서 x t x_t x t z z z ( 1 − α ‾ t ) ∇ x t log p ( x t ) \bigl(1 - \overline{\alpha}_t\bigr)\,\nabla_{x_t}\,\log p(x_t) ( 1 − α t ) ∇ x t log p ( x t ) Σ z ∇ z log p ( z ) \Sigma_z \nabla_z\,\log p(z) Σ z ∇ z log p ( z )
따라서 x 0 x_0 x 0
x 0 = x t + ( 1 − α ‾ t ) ∇ x t log p ( x t ) α ‾ t . x_0 = \frac{x_t \;+\; \bigl(1 - \overline{\alpha}_t\bigr)\,\nabla_{x_t}\,\log p(x_t)}{\sqrt{\overline{\alpha}_t}}. x 0 = α t x t + ( 1 − α t ) ∇ x t log p ( x t ) .
3. 다시 μ q ( x t , x 0 ) \mu_q(x_t, x_0) μ q ( x t , x 0 )
Reverse Process에서의 진짜(mean) 분포 q ( x t − 1 ∣ x t , x 0 ) q(x_{t-1} \mid x_t, x_0) q ( x t − 1 ∣ x t , x 0 )
μ q ( x t , x 0 ) = α t ( 1 − α ‾ t − 1 ) x t + α ‾ t − 1 ( 1 − α t ) x 0 1 − α ‾ t . \mu_q(x_t, x_0) = \frac{ \sqrt{\alpha_t\,(1-\overline{\alpha}_{t-1})}\,x_t \;+\; \sqrt{\overline{\alpha}_{t-1}\,(1-\alpha_t)}\,x_0 }{ 1 - \overline{\alpha}_t }. μ q ( x t , x 0 ) = 1 − α t α t ( 1 − α t − 1 ) x t + α t − 1 ( 1 − α t ) x 0 .
ver. 3에서는 x 0 x_0 x 0 x 0 = x t + ( 1 − α ‾ t ) ∇ x t log p ( x t ) α ‾ t x_0 = \frac{x_t + (1 - \overline{\alpha}_t)\,\nabla_{x_t}\,\log p(x_t)}{\sqrt{\overline{\alpha}_t}} x 0 = α t x t + ( 1 − α t ) ∇ x t l o g p ( x t )
μ q ( x t , x 0 ) = 1 α t x t + 1 − α t α t ∇ x t log p ( x t ) . \mu_q(x_t, x_0) = \frac{1}{\sqrt{\alpha_t}}\,x_t \;+\; \frac{1 - \alpha_t}{\sqrt{\alpha_t}}\,\nabla_{x_t}\,\log p(x_t). μ q ( x t , x 0 ) = α t 1 x t + α t 1 − α t ∇ x t log p ( x t ) .
즉, Tweedie's Formula 를 이용하면,μ q \mu_q μ q x t x_t x t
4. KL 발산 최소화 & 새로운 파라미터화
우리가 학습할 Reverse 분포 p θ ( x t − 1 ∣ x t ) p_\theta(x_{t-1} \mid x_t) p θ ( x t − 1 ∣ x t ) N ( x t − 1 ; μ θ ( x t , t ) , Σ q ( t ) ) \mathcal{N}\!\bigl(x_{t-1};\,\mu_\theta(x_t, t),\,\Sigma_q(t)\bigr) N ( x t − 1 ; μ θ ( x t , t ) , Σ q ( t ) ) μ q \mu_q μ q KL 발산 을 최소화하는 문제는,
arg min θ K L ( N ( x t − 1 ; μ q , Σ q ( t ) ) ∥ N ( x t − 1 ; μ θ , Σ q ( t ) ) ) , \arg\min_\theta \;KL\!\Bigl( \mathcal{N}(x_{t-1};\,\mu_q,\Sigma_q(t)) \;\big\|\; \mathcal{N}(x_{t-1};\,\mu_\theta,\Sigma_q(t)) \Bigr), arg θ min K L ( N ( x t − 1 ; μ q , Σ q ( t ) ) ∥ ∥ ∥ N ( x t − 1 ; μ θ , Σ q ( t ) ) ) , 다시 말해,
arg min θ 1 2 σ q 2 ( t ) ∥ μ θ ( x t , t ) − μ q ( x t , x 0 ) ∥ 2 . \arg\min_\theta \;\frac{1}{2\,\sigma_q^2(t)}\, \bigl\|\mu_\theta(x_t, t) - \mu_q(x_t, x_0)\bigr\|^2. arg θ min 2 σ q 2 ( t ) 1 ∥ ∥ ∥ μ θ ( x t , t ) − μ q ( x t , x 0 ) ∥ ∥ ∥ 2 .
ver. 3의 관점 에서는, μ q ( x t , x 0 ) \mu_q(x_t, x_0) μ q ( x t , x 0 )
1 α t x t + 1 − α t α t ∇ x t log p ( x t ) \frac{1}{\sqrt{\alpha_t}}\,x_t \;+\; \frac{1 - \alpha_t}{\sqrt{\alpha_t}}\,\nabla_{x_t}\,\log p(x_t) α t 1 x t + α t 1 − α t ∇ x t log p ( x t ) 로 표기할 수 있으므로,기울기(Score) ∇ x t log p ( x t ) \nabla_{x_t}\,\log p(x_t) ∇ x t log p ( x t ) 를 직접 예측하도록
즉, 노이즈 예측 (ver. 2) 대신,Score 예측 (ver. 3) 방식도 동등 하게 KL 발산을 최소화할 수 있다는 것이 결론입니다.
5. 요약
Tweedie's Formula :
E [ μ z ∣ z ] = z + Σ z ∇ z log p ( z ) \mathbb{E}[\mu_z \mid z] = z + \Sigma_z\,\nabla_z\,\log p(z) E [ μ z ∣ z ] = z + Σ z ∇ z log p ( z ) 가우시안 샘플 z z z 사후평균 을 “z + (log-likelihood 기울기) z + \text{(log-likelihood 기울기)} z + (log-likelihood 기울기 )
이를 x t x_t x t x 0 x_0 x 0 x 0 x_0 x 0 μ q ( x t , x 0 ) \mu_q(x_t, x_0) μ q ( x t , x 0 ) x t x_t x t ∇ x t log p ( x t ) \nabla_{x_t}\,\log p(x_t) ∇ x t log p ( x t )
Reverse Process 의 μ q \mu_q μ q
1 α t x t + 1 − α t α t ∇ x t log p ( x t ) \frac{1}{\sqrt{\alpha_t}}\,x_t + \frac{1 - \alpha_t}{\sqrt{\alpha_t}}\;\nabla_{x_t}\,\log p(x_t) α t 1 x t + α t 1 − α t ∇ x t log p ( x t ) 형태로 두고, 이를 근사하기 위해 Score(기울기) 를 예측하는 모델을 학습할 수 있음.
결국, 노이즈 예측 과 마찬가지로, Score 예측 역시동등한 파라미터화 로 볼 수 있음.
이로써 Other Equivalent Parameterizations ver. 3 는,Tweedie's Formula 를 활용하여 Score-Based 관점의 파라미터화를 제시한다는 점이 핵심입니다.
3.3 A Schematic Overview
3.4 From Scores to Samples: Langevin Dynamics
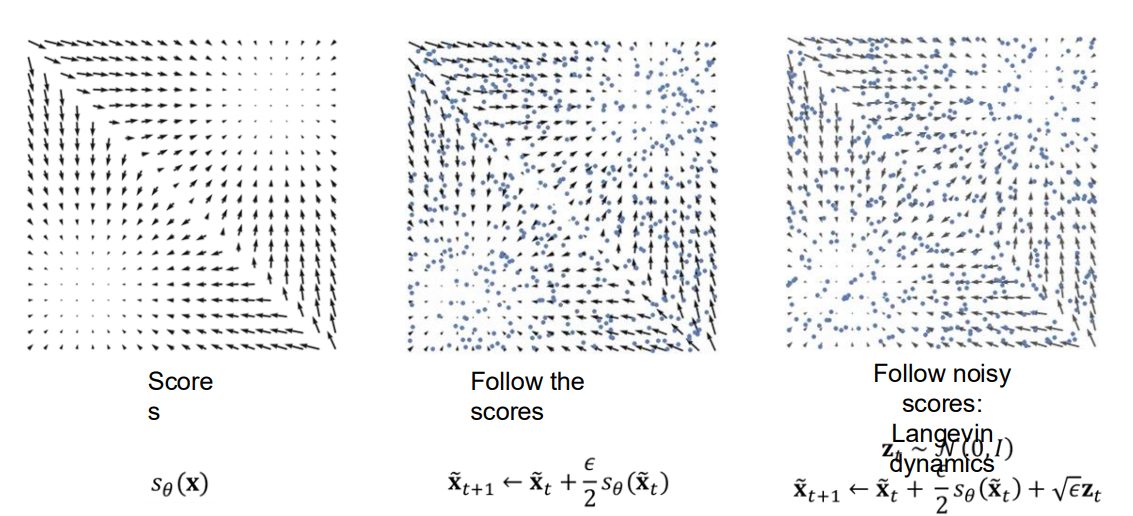
2차원 분포 예시
왼쪽 그림: Score 함수
화살표(벡터)들은 s θ ( x ) s_\theta(x) s θ ( x )
여기서는 사각형 모양의 데이터를 가정했을 때, 그 데이터 분포에 대응하는 Score가 어떤 방향을 갖는지를 시각화한 것이다.
화살표가 분포의 바깥쪽에서 안쪽으로 향하거나, 혹은 특정 모서리를 따라 방향이 달라지는 모습 등을 볼 수 있다.
가운데 그림: Score를 직접 따라가는(Deterministic) 업데이트
점(파란색으로 표시된 샘플들)이 초기 위치에서부터, x t + 1 ~ = x t ~ + ϵ 2 s θ ( x t ~ ) x_{\tilde{t+1}} = x_{\tilde{t}} + \frac{\epsilon}{2} s_\theta(x_{\tilde{t}}) x t + 1 ~ = x t ~ + 2 ϵ s θ ( x t ~ )
즉, 각 점이 Score 벡터가 가리키는 방향으로 조금씩 업데이트된다.
잡음 없이 오로지 Score의 방향만을 따라가다 보면, 최종적으로 데이터 분포가 모이는 특정 영역에 정렬되는 경향을 보인다.
오른쪽 그림: Langevin Dynamics
가운데 그림의 업데이트 식에 노이즈 항을 추가한 형태, 즉 x t + 1 ~ = x t ~ + − ϵ 2 s θ ( x t ~ ) + ϵ z t x_{\tilde{t+1}} = x_{\tilde{t}} + \frac{-\epsilon}{2} s_\theta(x_{\tilde{t}}) + \sqrt{\epsilon} z_t x t + 1 ~ = x t ~ + 2 − ϵ s θ ( x t ~ ) + ϵ z t z t ∼ N ( 0 , I ) z_t \sim \mathcal{N}(0, I) z t ∼ N ( 0 , I )
Score를 따라가되, 매 스텝마다 무작위 잡음을 섞어주어 샘플들이 확률적으로 움직인다.
결과적으로 MCMC (마르코프 연쇄 몬테카를로) 방식인 Langevin 샘플링 을 통해, 점들이 보다 부드럽게(확률적으로) 해당 분포에 모이게 된다.
3.5 Score-based Generative Modeling with SDEs
Score-based Generative Modeling 을 확률미분방정식(SDE) 관점에서 해석한 그림이다.
Forward SDE (데이터 → 노이즈)
식: d x = f ( x , t ) d t + g ( t ) d w dx = f(x, t)\,dt + g(t)\,dw d x = f ( x , t ) d t + g ( t ) d w
시간이 0 0 0 T T T
이 과정을 정방향 과정(Forward Process) 혹은 순방향 확산 이라고도 부른다.
Reverse SDE (노이즈 → 데이터)
식: d x = [ f ( x , t ) − g 2 ( t ) ∇ x log p t ( x ) ] d t + g ( t ) d w dx = [f(x, t) - g^2(t)\,\nabla_x \log p_t(x)]\,dt + g(t)\,dw d x = [ f ( x , t ) − g 2 ( t ) ∇ x log p t ( x ) ] d t + g ( t ) d w
Forward SDE의 반대 방향으로 진행하여, 노이즈 상태 에서 데이터 상태 로 샘플을 복원한다.
여기서 g 2 ( t ) ∇ x log p t ( x ) g^2(t)\,\nabla_x \log p_t(x) g 2 ( t ) ∇ x log p t ( x )
실제 샘플링 시에는, 시간 T T T x ( T ) x(T) x ( T )
4. 후기
와 생성형 AI가 이렇게 어려울 줄은 몰랐다. 정말 많은 수식이 필요한것 같다. 계속 보다보면 알 수 있다..!! ϕ \phi ϕ