1. Score based generative model

1.1 Representation of Probability Distributions

생성 모델(Generative Model)에서 확률분포를 어떻게 표현하고 학습할 수 있는지를 설명하겠습니다.다음과 같은 핵심 아이디어들이 포함되어 있습니다:

(1) 에너지 기반 모델(Energy-Based Model) 형태의 확률분포

• 식:
  $p_\theta(x) = \dfrac{e^{-f_\theta(x)}}{Z_\theta}$

  여기서

  • $f_\theta(x)$: 에너지 함수(Energy Function) 또는 부정적 로그-확률에 해당
  • $Z_\theta$: 정규화 상수(Partition Function).
    • $Z_\theta = \int e^{-f_\theta(x)} dx$ (연속형), 또는 $\sum_x e^{-f_\theta(x)}$ (이산형).
    • 전체 확률분포가 1이 되도록 정규화해주는 역할을 함.

• 학습 목표:
  $\max_{\theta} \sum_{i=1}^{N} \log p_\theta(x_i)$
  이는 관측된 데이터의 로그우도(Log-likelihood)를 최대화하는 방식으로, 모델 파라미터 $\theta$를 학습함.

(2) 명시적(Explicit) 모델 vs. 암묵적(Implicit) 모델

1. Explicit Models:
   • 명시적으로 확률분포 $p_\theta(x)$ 자체를 정의함(또는 확률질량함수/밀도함수를 가정).
   • 예시:
     • Bayesian Networks (VAEs 등)
     • Markov Random Field
     • Autoregressive Models
     • Flow Models
   • 이들은 분포의 형태나 구조를 설계하여, 확률변수 $x$가 어떻게 분포되는지 직접적으로 정의하고 추론하는 특징이 있음.

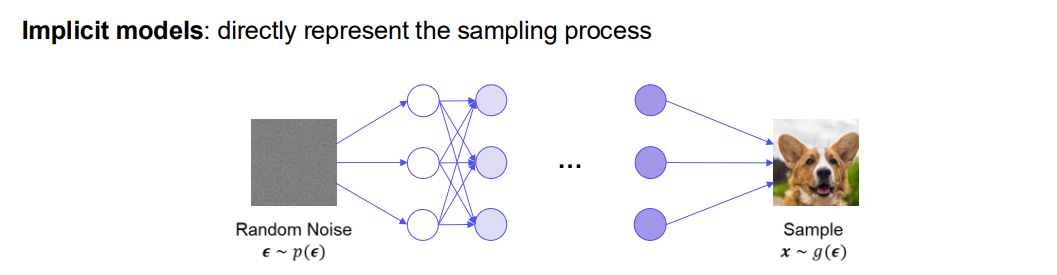
2. Implicit Models:
   • 확률분포를 직접 식으로 표현하지 않고, “샘플링 과정(Sampling Process)”을 학습함.
   • 예시: GAN(Generative Adversarial Network)
     • 임의 잡음 $\epsilon \sim p(\epsilon)$을 네트워크에 입력 → 생성 모델 $g_\theta(\epsilon)$ → 샘플 $x$ 생성.
   • $p_\theta(x)$를 명시적으로 계산할 수 없지만, 샘플링으로부터 “데이터를 만들어내는 과정” 자체를 모델링.

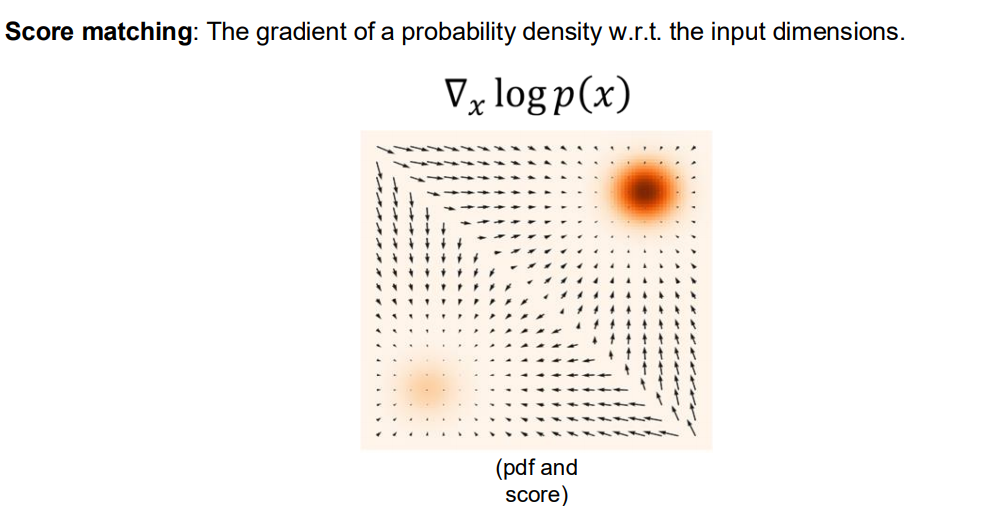
(3) Score Matching: 확률분포의 로그 미분(Score) 활용

• Score란, 확률밀도함수의 로그에 대한 그라디언트(gradient), 즉 $s_\theta(x) = \nabla_x \log p_\theta(x)$
  를 의미합니다.

• 에너지 기반 모델 식을 대입하면, $\log p_\theta(x) = -f_\theta(x) - \log Z_\theta$ 이므로,

  $\nabla_x \log p_\theta(x) = -\nabla_x f_\theta(x) - \nabla_x \log Z_\theta.$

• $\log Z_\theta$는 $x$에 대한 적분/합이기 때문에, 대개 $x$에 대해 상수로 취급되어 $\nabla_x \log Z_\theta \approx 0,$
  라고 볼 수 있습니다(물론 $\theta$에 대한 미분은 상수가 아님).

• 따라서 Score는 보통

  $s_\theta(x) = -\nabla_x f_\theta(x)$

  로 단순화할 수 있습니다.

• 오른쪽 그림에서 볼 수 있듯, Score 벡터 필드는 분포가 높은 곳(우도/밀도가 큰 영역)을 향해 방향을 갖추며, 여기서 Score Matching은 “모델의 Score가 실제 데이터 분포의 Score와 닮도록(가깝도록) 학습”하는 기법입니다.
  

(4) 결론 요약

1. 에너지 기반 모델 형태:
   $p_\theta(x) = \dfrac{e^{-f_\theta(x)}}{Z_\theta}$.

   • $Z_\theta$는 정규화 상수로, 분포가 확률로서의 성질(총합=1)을 지키도록 해줌.

2. 명시적 vs. 암묵적(Implicit) 모델:

   • 명시적 모델은 확률분포를 직접 정의하고, 로그우도를 최대화함.
   • 암묵적 모델은 샘플 생성 과정을 학습하며, 확률분포를 명시적으로 표현하지 않음.

3. Score Matching:

   • 확률밀도의 로그에 대한 그라디언트(Score)와 실제 분포의 Score가 가까워지도록 하는 방식.
   • 확률분포의 형태(어디가 높고 어디가 낮은지)를 미분 정보를 통해 학습할 수 있음.

이와 같은 과정을 통해, 생성 모델은 데이터를 모사하거나 새로운 샘플을 만들어낼 수 있는 확률분포를 학습하게 됩니다. 특히 Score-Based Generative Modeling은 분포의 Score 함수($s_\theta(x)$)를 효과적으로 추정하여, 샘플링 시점에 Langevin Dynamics나 SDE(확률미분방정식)를 활용해 노이즈를 제거하고 데이터를 생성하는 기법으로 발전하고 있습니다.

1.2 Score Estimation

Score-based Generative Modeling에서 “데이터 분포 $p_{data}(x)$ 의 Score($\nabla_x \log p_{data}(x)$)를 어떻게 추정(Estimation)하는가”를 다루는지를 알아보겠습니다.

(1) 문제 정의

• Given: i.i.d. 샘플 $\{x_1, x_2, \dots, x_N\}$, 이들은 $p_{data}(x)$ 로부터 추출
• Task: 데이터 로그-우도의 그라디언트 $\nabla_x \log p_{data}(x)$ (즉 Score)를 추정하는 것
• Score Model: 학습 가능한 벡터값 함수 $s_{\theta}(x): \mathbb{R}^D \rightarrow \mathbb{R}^D$
• Objective: 실제 Score인 $\nabla_x \log p_{data}(x)$와 모델 $s_{\theta}(x)$라는 두 벡터장을 어떻게 비교할까?

이때, 우리가 원하는 것은 “데이터 분포로부터 샘플링한 지점들에서 $\nabla_x \log p_{data}(x)$에 가깝도록 $s_{\theta}(x)$를 학습”하는 것입니다.

(2) 왜 Score를 직접 추정할까?

• Score Matching 기법은 데이터 분포 자체를 명시적으로 몰라도, “로그-우도의 그라디언트”를 추정함으로써 확률분포의 형태(어디에서 확률이 높고 낮은지)를 배울 수 있게 합니다.
• Score-based Generative Model에서는 이 추정된 Score를 이용해 샘플링(예: Langevin Dynamics, SDE 역방향 해석)으로 데이터를 생성합니다.

(3) Score Matching 손실함수: Fisher Divergence

• 목표:
  $\frac{1}{2} \mathbb{E}_{p_{data}} \Big[ \big\lVert \nabla_x \log p_{data}(x) \;-\; s_{\theta}(x) \big\rVert_{2}^{2} \Big].$

• 이는 Fisher Divergence로 불리며, 두 벡터장(실제 Score와 추정 Score)의 유클리디안 거리를 최소화하는 방식입니다.($\frac{1}{2}$을 곱해주는 이유는 미분(최적화) 시 편의를 위해서입니다.)

• Hyvärinen (2005)의 Score Matching 논문에서 제시된 결과에 따르면, 이 항을 직접 최소화하는 대신,
  $\mathbb{E}_{p_{data}} \Big[\frac{1}{2} \lVert s_{\theta}(x)\rVert_{2}^{2} \;+\; \mathrm{trace}\big(\nabla_x s_{\theta}(x)\big)\Big]$
  형태로 변형할 수 있습니다. (적분 부분적분 기법 활용)

(4) 수식 전개 (스칼라 예시)

그림 속 수식은 스칼라 $x$에 대해,
$\frac{1}{2} \int p_{data}(x)\big(\nabla_x \log p_{data}(x) \;-\; s_{\theta}(x)\big)^2 \, dx$
를 전개해보면, 경계항이 사라지고 결과적으로

$\mathbb{E}_{p_{data}}\Big[\frac{1}{2}\lVert s_{\theta}(x)\rVert_{2}^{2} \;+\; \mathrm{trace}\big(\nabla_x s_{\theta}(x)\big)\Big]$

와 동등해진다는 과정을 보여줍니다.

이를 통해 Score Matching 손실을 계산할 때, 실제 $\nabla_x \log p_{data}(x)$를 몰라도 모델 $s_{\theta}(x)$의 노름과 그 다이버전스(Trace of Jacobian)를 이용해 간단히 구현할 수 있음이 강조됩니다.

(5) 결론 및 요약

1. Score Estimation:

   • 우리가 가진 데이터로부터 실제 Score(로그-우도의 그라디언트)를 직접 계산하기는 어려움.
   • 대신, 학습 가능한 함수 $s_{\theta}(x)$가 그 Score를 흉내내도록 학습한다.

2. Score Matching (Hyvärinen, 2005):

   • Fisher Divergence를 최소화해서 $\nabla_x \log p_{data}(x)$와 $s_{\theta}(x)$가 가깝게 함.
   • 경계 조건이 적절하다면, $\mathbb{E}_{p_{data}} \lVert \nabla_x \log p_{data}(x) \;-\; s_{\theta}(x) \rVert^2$ 를
     $\mathbb{E}_{p_{data}}\big[\frac{1}{2}\lVert s_{\theta}(x)\rVert^{2} + \mathrm{trace}(\nabla_x s_{\theta}(x))\big]$ 로 바꿔 계산 가능.

3. 의의:

   • 복잡한 확률분포를 명시적으로 추정하지 않고도, 분포의 “기울기” 정보를 학습함으로써 생성 모델에 활용할 수 있음.
   • 현대의 Score-based Generative Modeling(예: DDPM, SGM 등)에서 중요한 이론적 기반이 됨.

정리하면, “어떻게 실제 데이터 분포의 Score를 추정할 것인가?”에 대해 Score Matching은 매우 효율적인 해답을 제시합니다. 이 기법을 통해, 분포 자체의 Normalizing Constant (정규화 항) 없이도 기울기를 학습할 수 있다는 점이 큰 장점입니다.

1.3 From Scores to Samples: Langevin Dynamics

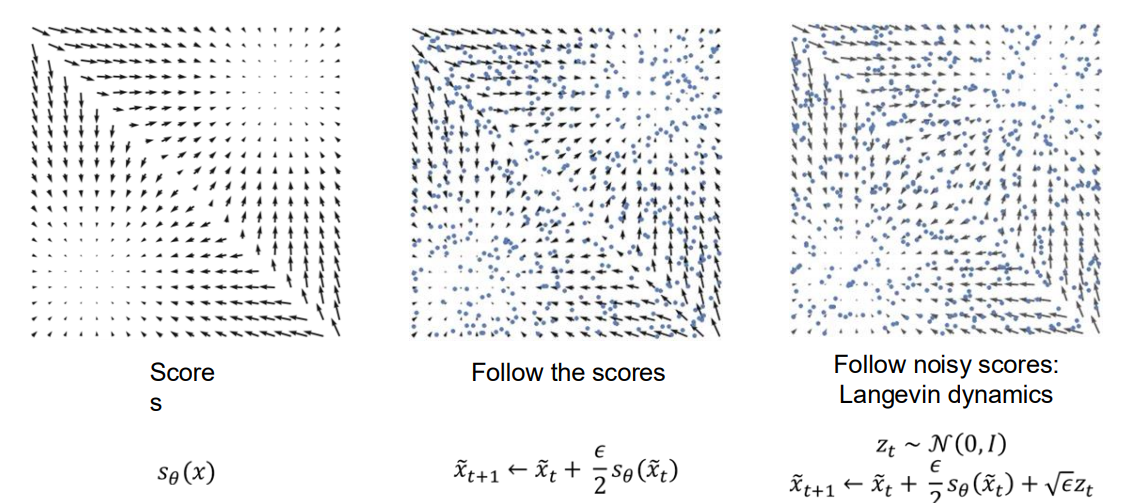
위 이미지는 Score-based Generative Modeling에서 학습한 Score를 활용해 샘플을 생성하는 과정을 시각적으로 보여줍니다.

1. 왼쪽 그림: 학습된 Score $s_\theta(x)$

   • 2차원 장난감 예시에서, 화살표 벡터들이 각 위치 $x$에서의 Score(로그 확률밀도의 기울기 방향)를 나타냄.
   • 분포 내부 방향으로 화살표가 형성되며, 높은 확률밀도 쪽을 가리키는 형태.

2. 가운데 그림: Follow the Scores (Deterministic Update)

   • 점(파란색)들이 초기 위치에서부터 $x_{\tilde{t+1}} = x_{\tilde{t}} + \frac{\epsilon}{2} s_\theta(x_{\tilde{t}})$ 식으로 업데이트.
   • 화살표를 순수하게 따라 이동하기 때문에, 잡음이 없고 데이터 분포 중심을 향해 수렴하는 모습을 보임.

3. 오른쪽 그림: Langevin Dynamics (Noisy Update)

   • 랜덤 잡음을 섞어주는 방식:
     $x_{\tilde{t+1}} = x_{\tilde{t}} + \frac{\epsilon}{2} s_\theta(x_{\tilde{t}}) + \sqrt{\epsilon} \, z_t,$
     여기서 $z_t \sim \mathcal{N}(0,I)$
   • 매 스텝마다 작은 스텝 사이즈($\epsilon$)로 Score 방향으로 이동하되, 가우시안 잡음도 추가 → MCMC 샘플링과 유사한 방식.
   • 결과적으로 확률분포 전체를 탐색하며 최종 분포에 맞는 샘플을 생성.

1.4 Score-based Generative Modeling

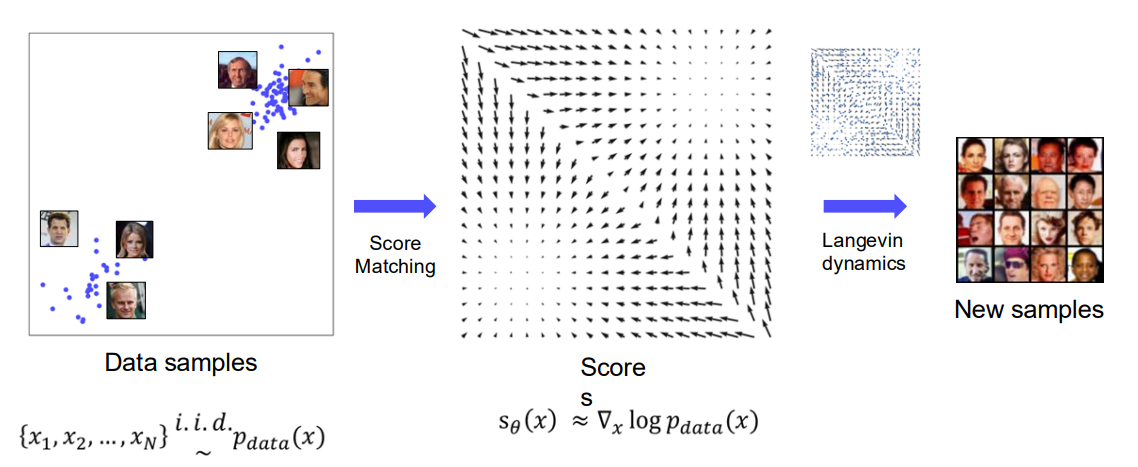
위 이미지는 Score-based Generative Modeling 전체 과정을 요약적으로 나타냅니다.

1. Data samples

   • 우리가 가진 실제 데이터 $\{x_1, x_2, \dots, x_N\} \sim p_{data}(x)$
   • 이미지 예시에서는 얼굴 사진들이 2차원 상에 놓여 있는 형태로 시각화.

2. Score Matching

   • 데이터 분포의 Score, 즉 $\nabla_x \log p_{data}(x)$를 추정하기 위해 모델 $s_\theta(x)$를 학습.
   • 에너지 기반 모델(Energy-Based Model) 관점에서는 $s_\theta(x) \approx -\nabla_x f_\theta(x)$.

3. Sampling with Langevin Dynamics

   • 학습된 Score $s_\theta(x)$를 이용해, 노이즈에서부터 샘플을 점진적으로 이동시키는 방식.
   • 2차원 예시에서의 벡터장을 따라 이동하듯이, 실제 고차원 얼굴 이미지 영역에서도 점들을 이동시켜 새로운 이미지를 생성.

4. New samples

   • 최종적으로, 분포 $p_{data}(x)$를 모사하는 새로운 이미지(샘플)들을 생성할 수 있음.
   • 예시 그림에서는 사람 얼굴 이미지가 생성된 결과를 보여줌.

1.5 Adding Noise to Data for Well-Defined Scores

여기서는 Score의 안정적인 학습을 위해, “데이터에 노이즈를 추가”하는 방법을 설명합니다.

• 문제점:

  • Scores can be undefined
    • 데이터 분포의 지지가 저차원 매니폴드 위에 있거나(예: 매우 희소한 영역),
    • 데이터가 이산적일 경우, $\log p_{data}(x)$가 스무스하지 않아 기울기(Score)가 정의되기 어려움.

• 해결책: 작은 가우시안 잡음 추가

  • 예) $x \leftarrow x + \sigma \cdot \epsilon$, $\epsilon \sim \mathcal{N}(0, I)$
  • 이렇게 노이즈를 더해 연속적이고 부드러운 분포로 만들어주면, Score가 명확해지고 학습 손실도 안정화됨(그래프에서 오른쪽 그림).
    

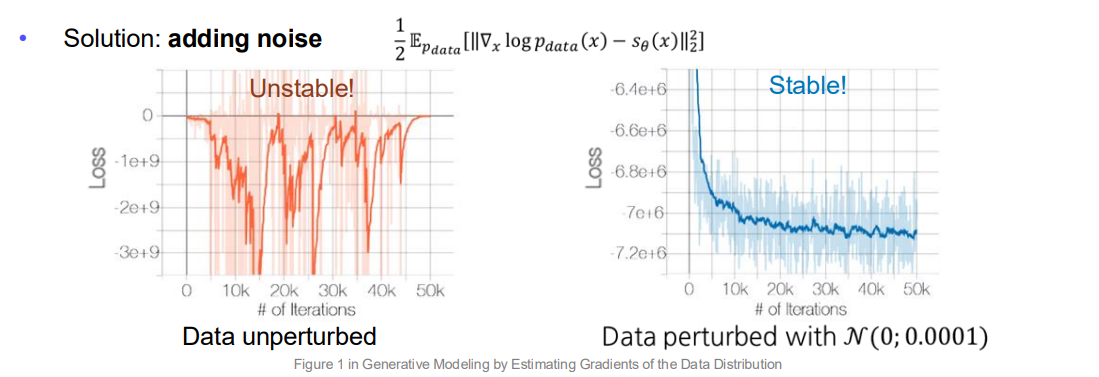
• 결과:

  • 노이즈가 없는 경우(왼쪽)는 학습 손실이 불안정하게 튀는 반면,
  • 노이즈를 추가한 경우(오른쪽)는 손실이 빠르게 낮아지고 안정된 값을 유지함.

즉, 데이터 분포가 너무 날카롭거나 이산적인 상황에서는 “노이즈 퍼터베이션”을 통해 스무스한 분포를 만들고, 그 위에서 Score Matching을 수행함으로써 더욱 안정적이고 명확한 학습이 가능하다는 점을 보여줍니다.

1.6 Challenge in Low Data Density Regions

Score-based Generative Modeling에서 저밀도 영역(low data density)에서 발생하는 문제점과 이를 어떻게 극복하는지를 보여주겠습니다.

(1) Slow Mixing of Langevin Dynamics

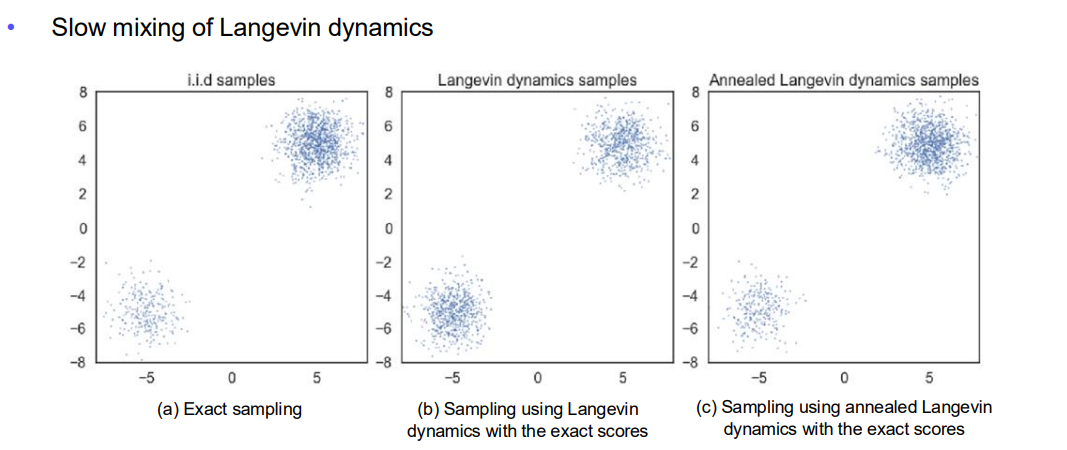
1. (a) Exact sampling

   • 왼쪽 그림은 실제 분포에서 i.i.d. 샘플을 정확히 뽑았을 때의 모습.
   • 분포가 두 개의 클러스터(위쪽, 아래쪽)로 나뉘어 있음.

2. (b) Sampling using Langevin Dynamics

   • 정확한 Score(즉, 실제 $\nabla_x \log p(x)$)를 사용해서 Langevin Dynamics로 샘플링한 결과.
   • 두 개의 모드(클러스터)가 존재하지만, Langevin Dynamics가 하나의 모드에서 다른 모드로 이동하는 데 시간이 오래 걸릴 수 있음(“slow mixing” 문제).
   • 즉, 한 클러스터에서 다른 클러스터로 점들이 잘 넘어가지 못해, 충분히 많은 스텝을 거쳐야 전 영역을 탐색할 수 있음.

3. (c) Sampling using Annealed Langevin Dynamics

   • “어닐링(annealing)” 기법을 추가한 Langevin Dynamics 샘플링.
   • 온도(또는 잡음 스케일)를 점차 줄여가며 분포를 탐색하기 때문에, 두 모드 사이를 좀 더 활발히 탐색할 수 있음.
   • 결과적으로 더 빠른 mixing(섞임)과 각 모드에 대한 더 균형 잡힌 샘플링이 가능해짐.

정리하자면, Langevin Dynamics는 많은 경우 MCMC 기반으로 mixing 속도가 느릴 수 있으며, 특히 저밀도 영역에서의 점프가 어렵습니다. Annealed Langevin Dynamics는 이러한 문제를 완화시키는 한 가지 방법이 됩니다.

(2) Inaccurate Score Estimation in Low Density Regions

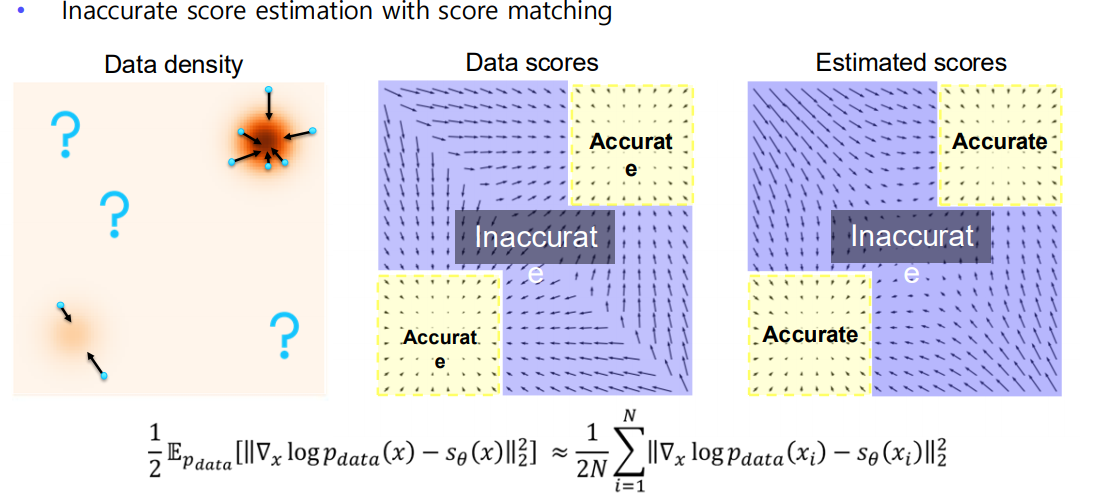
1. 데이터 밀도(Data density)

   • 그림에서 주황색으로 진한 부분이 데이터가 많이 몰린 영역(고밀도), 옅은 부분이나 바깥쪽이 저밀도 영역.

2. Data scores (실제 $\nabla_x \log p_{data}(x)$)

   • 분포 내부(샘플이 많은 영역)에서는 Score가 비교적 정확하게 추정 가능(“Accurate” 영역).
   • 하지만 샘플이 거의 없는 외곽이나 저밀도 영역(“Inaccurate” 영역)에서는 로그-우도를 직접 추정하기 어려움.

3. Estimated scores (추정된 $s_\theta(x)$)

   • 실제 데이터가 풍부한 곳에서는 모델이 Score를 잘 맞출 수 있지만,
   • 저밀도 영역에 대한 학습이 부족해 Score가 부정확할 수 있음.

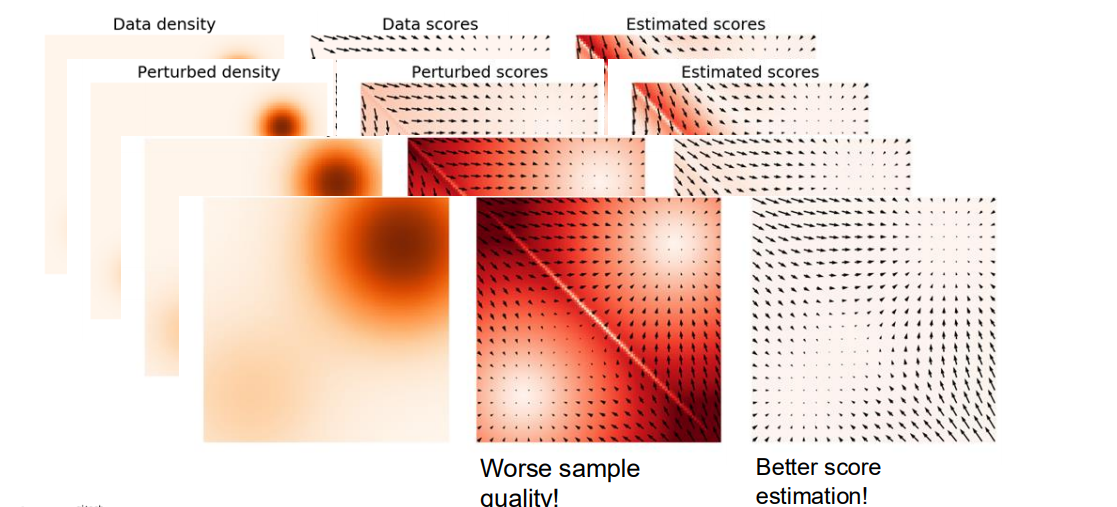
(3) Adding Noise to Data for Better Score Estimation

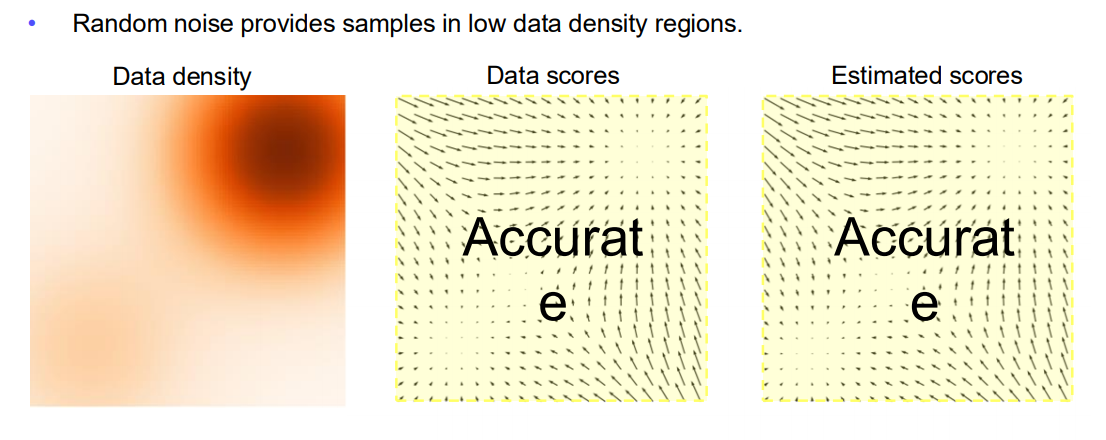
• 아이디어: 데이터 분포가 sparse(희소)하거나 저차원 매니폴드 위에 있을 때, 작은 가우시안 잡음을 더해서 범위를 넓혀주면, 저밀도 영역에도 일정 수준 샘플이 생김.

• 장점:

  1. 저밀도 영역에서도 Score를 학습할 수 있는 기회가 생김.
  2. 학습 안정성이 향상되고, 로스(loss)가 안정적으로 수렴함.

• 단점:

  • 노이즈가 너무 크면 “실제 데이터의 특성”이 많이 희석되어 샘플 품질이 떨어질 수 있음(“Worse sample quality!”).
  • 적절한 수준의 노이즈 스케줄링(Annealing) 기법이 필요.

최종 요약:

• 저밀도 영역에서 Score를 잘 추정하기 어렵다는 점이 Score-based Generative Modeling의 주요 과제 중 하나.
• Annealed Langevin Dynamics나 노이즈 추가 등의 기법을 사용해,
  • 샘플링에서의 slow mixing 문제를 완화하고,
  • Score 추정에서의 부정확성을 개선하려는 시도가 이루어져 왔음.

이로써, Score-based Generative Modeling은 데이터 분포 전역을 균형 있게 커버할 수 있도록, 다양한 노이즈 주입/어닐링/멀티 스케일 기법 등을 활용해 저밀도 영역 문제를 극복하려 합니다.

1.7 Annealed Langevin Dynamics

Annealed Langevin Dynamics(ALD)의 기본 아이디어를 소개합니다.

샘플링 과정에서, $\sigma_1 \to \sigma_2 \to \dots \to \sigma_L$ 처럼 노이즈 레벨을 점진적으로 낮춰가며(어닐링), 이전 단계에서 생성된 샘플을 다음 단계의 초기값으로 사용하는 방식입니다.

1. 샘플링 순서

   • 처음에는 큰 노이즈 스케일 $\sigma_1$을 사용해 분포 전역을 탐색하기 쉽도록 하고(클러스터 간 이동 등),
   • 점차 $\sigma_i$를 줄여가면서 샘플이 고밀도 영역에 정교하게 수렴하도록 유도합니다.

2. 그림 해석
   

   • 왼쪽($\sigma_1$): 비교적 큰 노이즈로 인해, 점(파란색 샘플)들이 분포 전역을 넓게 탐색하며 Score(오렌지 색상의 분포와 화살표) 방향으로 이동.
   • 중간($\sigma_2$): 노이즈 레벨을 줄였으므로, 이전보다 샘플들이 더 정밀하게 고밀도 영역으로 모이는 모습.
   • 오른쪽($\sigma_3$): 최종적으로 노이즈가 훨씬 작아져, 샘플들이 분포의 중심 부분(고밀도 영역)에 정확히 위치하게 됨.

1.8 Algorithm

• 입력:

  • ${\sigma_i}_{i=1}^L$: 노이즈 레벨들을 큰 순서대로 정렬
  • $ϵ$: 기본 스텝 사이즈(learning rate와 유사)
  • $T$: 각 노이즈 레벨별로 몇 번의 내부 스텝을 수행할지 결정

• 과정:

1. 큰 노이즈 스케일($\sigma_1$)부터 시작해서, 각 $\sigma_i$마다 Langevin Dynamics 스텝을 $T$번 반복
2. 스텝 사이즈 $\alpha_i$는 노이즈 레벨에 비례해 조정
3. 매 스텝마다 가우시안 잡음 $z_t \sim \mathcal{N}(0,I)$를 섞어주고, Score $s_\theta(\cdot, \sigma_i)$ 방향으로 이동
4. 마지막에 얻은 샘플($x̃_T$)을 다음 레벨의 초기값으로 설정

• 결과: 최종적으로 $\sigma_L$(가장 작은 노이즈) 단계에서 “분포 중심부”에 잘 수렴한 샘플을 얻게 됨.

1.10 Results: Inpainting

• 이미지에서 가려진 영역(masked area)에 대해, 점차 노이즈+Score를 사용해 복원(Inpainting)함.
• 마스크 $m$이 1인 부분은 “정해진 픽셀(원본)$y$”을 유지, 마스크가 0인 부분은 생성 과정으로 채움.
• 노이즈 레벨을 큰 $\sigma_i$부터 작은 $\sigma_L$까지 어닐링하며, 점진적으로 복원 품질을 높여감.

1.11 Conclusion

Score-based Generative Modeling 요약:

1. No need to be normalized/invertible

• 확률분포 정규화 항($Z_\theta$)이나 역변환 구조가 필요 없음
• 유연한 모델 아키텍처 선택 가능

2. No minimax optimization

• GAN처럼 제너레이터 vs. 디스크리미네이터의 적대적 학습이 아님
• 학습이 안정적이고, 학습 진행 정도를 자연스럽게 측정 가능

3. Adding noise + Annealing

• 데이터나 학습 과정에 노이즈를 주어 스코어 추정을 안정화
• 노이즈 레벨을 단계적으로 줄이는 어닐링 기법으로 샘플링 효율 향상

4. Better or comparable sample quality to GANs

• 실제 연구에서, Score 기반 모델들이 종종 GAN 수준의 샘플 품질을 보여주거나 더 좋음

결국 Score-based Generative Model은 확률분포의 Score를 직접 추정하고, 이를 이용해 Langevin Dynamics 또는 어닐링된 방정식을 풀어 데이터 샘플을 생성하는 접근입니다. 잡음+어닐링 전략이 매우 중요한 역할을 하며, 이 방법을 통해 GAN과 비견될 만한 혹은 뛰어난 샘플 품질이 가능해집니다.

1.12 후기

VAE diffusion 보다는 쉬웠지만, 정말 생성하나 하는데, 이렇게 많은 수식이 필요하다니 ㅠㅠ.
나는 똑똑한 사람들이 잘 만들 모델들을 가지고 시장에 적용해서 돈을 벌 생각을 하자~