
딥러닝 아자아자 화이팅!
출처
https://john-analyst.medium.com/회귀-regression-란-398c548e1560
https://aws.amazon.com/ko/what-is/linear-regression/
https://sooho-kim.tistory.com/85
https://yeong-jin-data-blog.tistory.com/entry/딥러닝-개념-비용함수-Cost-Function#:~:text=✅%20비용함수(Cost%20Function,%2C%20손실함수(Loss%20Function)&text=대표적인%20비용함수에는%20MAE%2C%20MSE%2C%20RMSE가%20있다.
https://dictionary.cambridge.org/ko/사전/영어/tangent#google_vignette
https://en.wikipedia.org/wiki/Convex_function
목차
- Linear regression
- Hypothesis
- Cost function
- How to minimize cost function

Regression(회귀)가 뭐죠?
가장 기초적인 것도 헷갈려 하다니 스스로에게 좀 당황스럽다.
회귀는 말 그대로 여러개의 독립변수 x와 하나의 종속변수 y 간의 상관관계를 모델링하는 기법이다.
Linear regression?
Linear하면 직선!! 의 이미지가 떠오르지 않는가? 맞다 말그대로
Straight line 을 의미한다.
그렇다면 Linear regression은 그대로 해석했을 때, 선형 회귀이다.
선형회귀는 이미 알려진 다른 데이터값을 이용해 새로운 데이터가 주어졌을 때, 그 값을 예측하는 기법이다.
linear regression은 correlation of the data를 linear한 equation으로 나타내는 것이다. 따라서 데이터 분포가 linear할 때 효과적!
Hypothesis
그런데 그렇다면 의문이 두개가 생긴다.
- 공식을 만들 수 있다고 했는데 뭐가 가장 좋은 솔루션인지 어떻게 아는가?
- 어떻게 그 공식을 찾아내는가?
물론 기본적 고등 교육을 받았다면 너무나도 자연스럽게 찾아낼 수 있을 것이다. 하지만 질문은 이거다.
왜 그렇게 생각했는가??
regression은 가장 최적의 parameter를 찾아내는 과정이라고 할 수 있다.
위에서 말했듯 독립변수와 종속변수라고 하지 않았는가?
y는 x를 통해 도출된다. 하지만 x는 변수이다. 말 그대로 변하는 수라는 의미이다.
그렇다면 우리는 w와 b를 찾아야 한다!
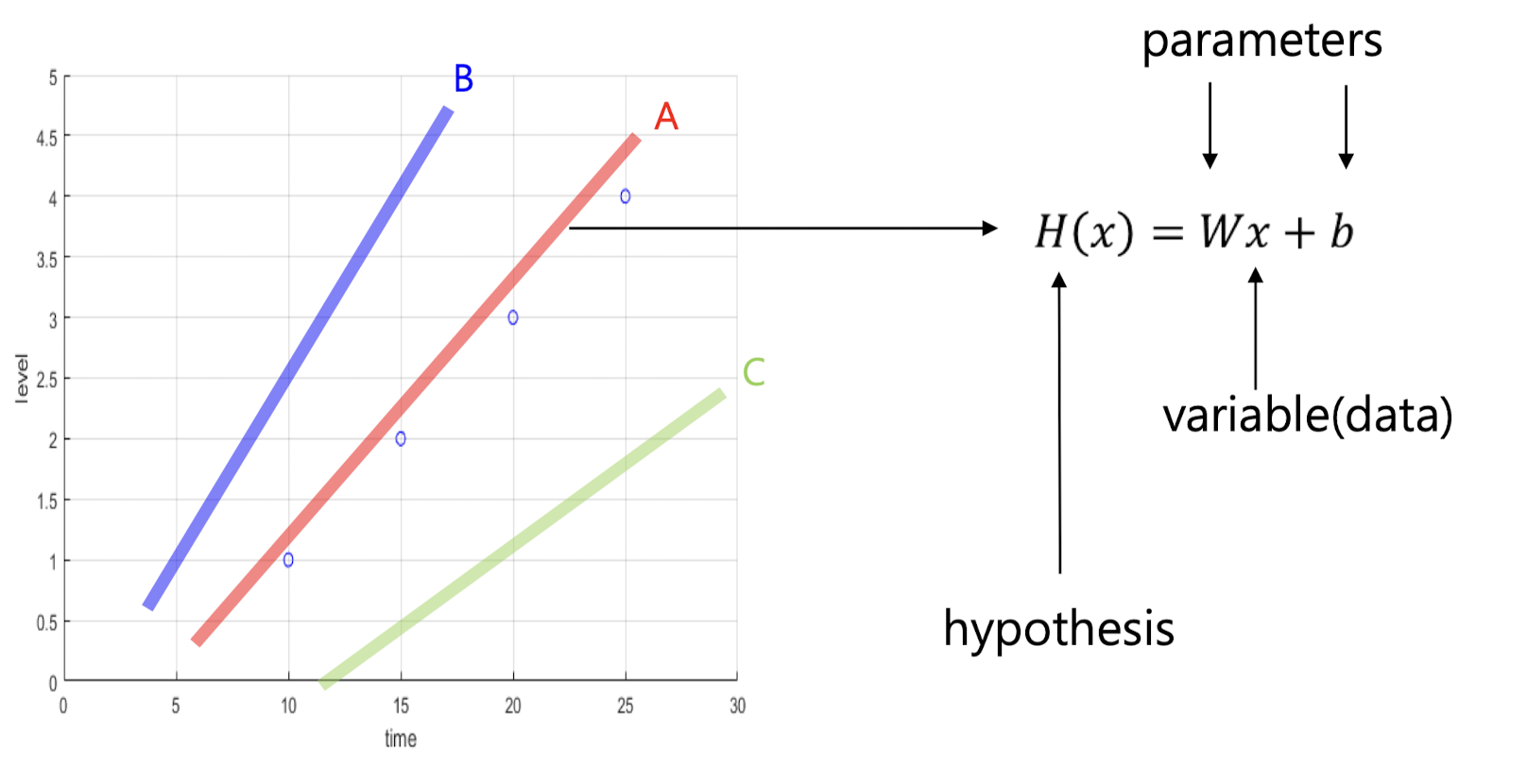
W와 b는 parameter라고 부른다.
cost function (=loss functrion)
그럼 우린 이제 cost function을 정의해야 한다.
근데 난 지금 cost function이 정확히 뭘 의미하는지도 기억이 안난다.. 반성 또 반성
Cost function이란?
주어진 값 x에 대해 정의한 hypothesis와 실제 데이터 y간의 차이를 의미.
- MSE(Mean Squared Error)같은 공식을 사용한다!
cost function의 목표는 cost를 0으로 만드는 hypothesis를 찾는 것!
근데 그렇다면 생기는 새로운 의문
굳이 복잡한 MSE가 아니라
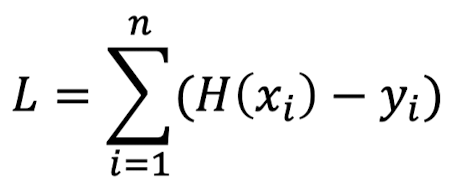
이런 공식을 사용하면 안되는건가?
➡️ 당연히 안된다!!!
결과값이 음수와 양수로 나오니 합쳐졌을때 에러가 발생해도 0이란 값으로 착각이 가능하다.
그래서 MAE(mean absolute error)와 같이 절댓값을 씌우는 손실함수도 존재한다!
Cost function 종류
cost function은 error를 양수로 만들어주는 공식이 필요함
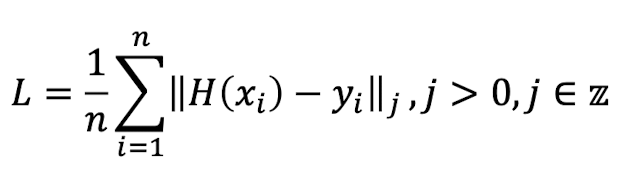
여기서 L의 의미는 "Lebesgue"라는 사람을 의미한다고 한다. 별거 아닌듯
- L1 norm: 위에서 말한 MAE가 L1 norm이다. j값이 1인 경우이다.
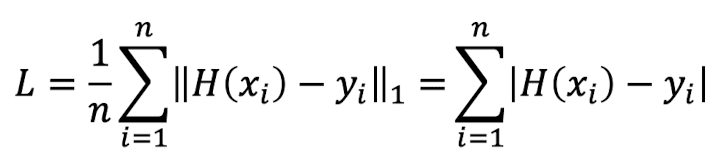
- L2 norm: 위에서 말한 MSE가 L2 norm이다. j값이 2인 경우이다.
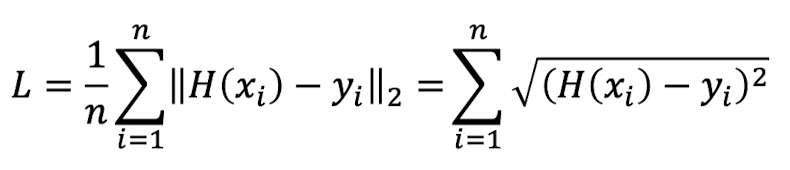
How to minimize cost function
그렇다면 다시 의문등장 ㅎ
어떻게! 위에서 정의한 cost function을 줄일 것인가?
이제부터 그 방식에 대해 알아보겠다.
Exhaustive search
냅다 다 뒤져보기 전법!
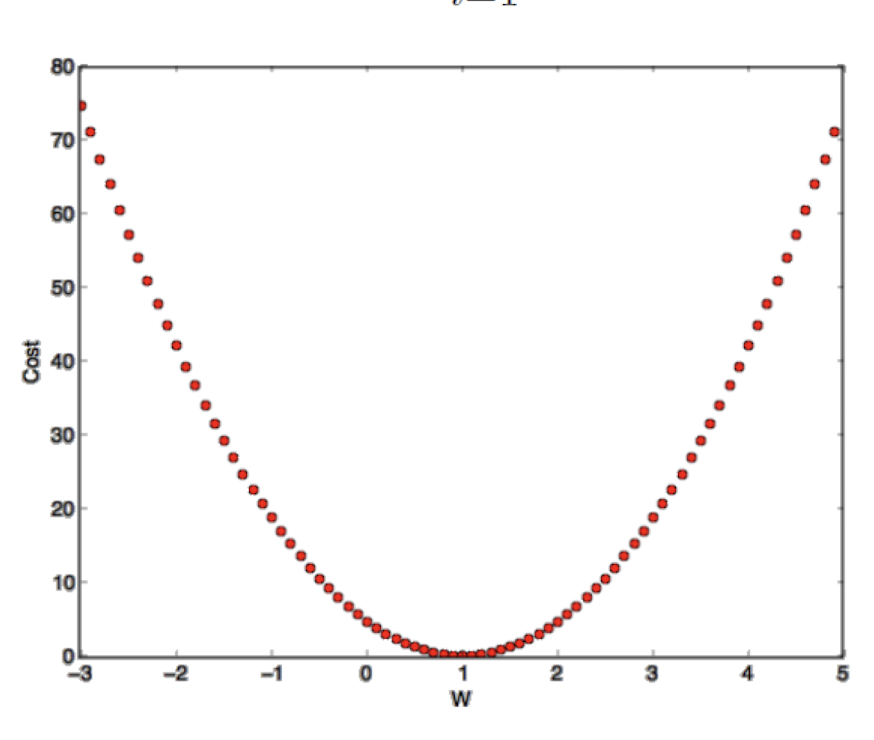
위의 x와 y값에 대해 하나하나 cost function을 적용해 error값을 찾아내는 방식.
딱봐도 머리아프다 기각!
Jump to the opposite direction of the tangent
tangent의 정확한 뜻이 뭘까 좀 고민했다.
tangent는 곡선에 접하는 접선을 의미한다.
접선의 반대 방향으로 점프(건너뛰며) 진행하는 방식이다.
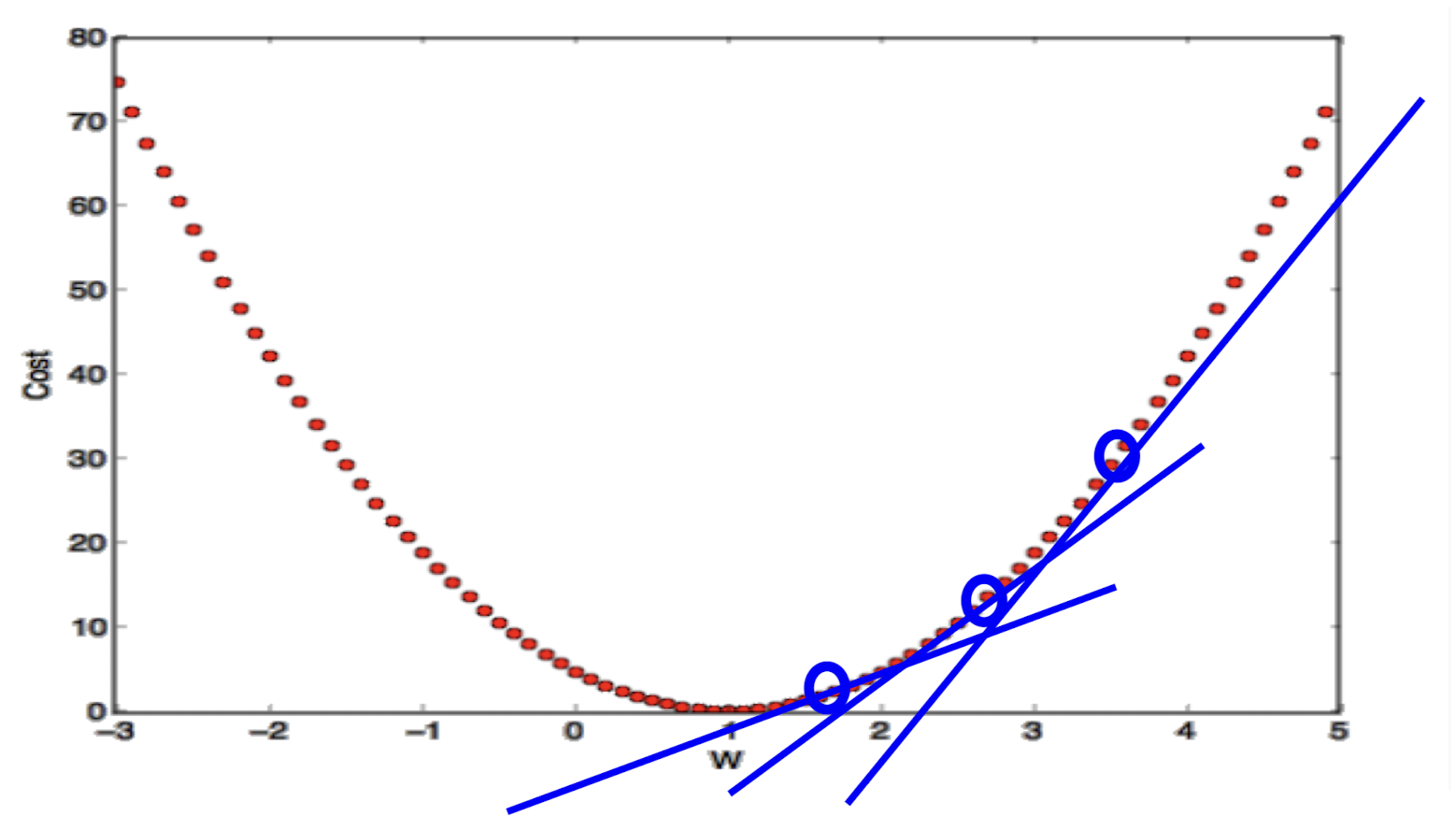
딱봐도 이게 정답일 것 같지 않는가? 시간도 없고 자원도 부족한데 언제 얼마나 많을지도 모르는 데이터를 하나하나 뒤져보고 앉아있을 것인가.
그래서 등장한다
Gradient Descent Algorithm
이다!
one takes steps proportional to the negative of the gradient (or approximate gradient) of the function at the current point.
영어로 적으니까 나도 이해 안된다ㅎㅎ
현재 포인트의 기울기의 음수에 비례하는 다음 단계를 수행하는 것이 gradient descent이다.
그렇다면 이제 다시 내 공부의 가장 중요한 부분이 등장할 차례이다.
gradient는 뭐고 descent는 뭘까?
gradient: 기울기
descent: 하강
그렇다. 바로 경사하강법! 기울기를 줄여가며 진행하는 방식이라는 것이다.
공식은 아래와 같다.

여기서 보이는 알파는 LR이다.
높을수록 값이 튀고 낮을수록 최소 cost를 찾는데 오랜 시간이 걸린다. 이부분은 뒤에서 마저 ...
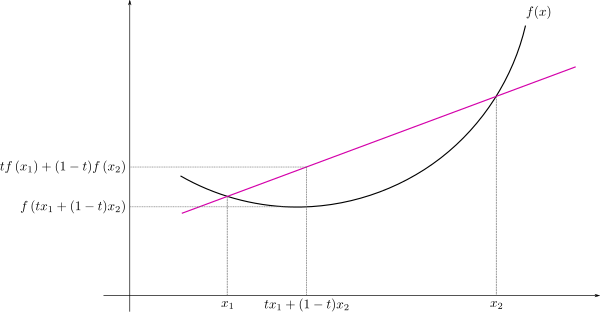
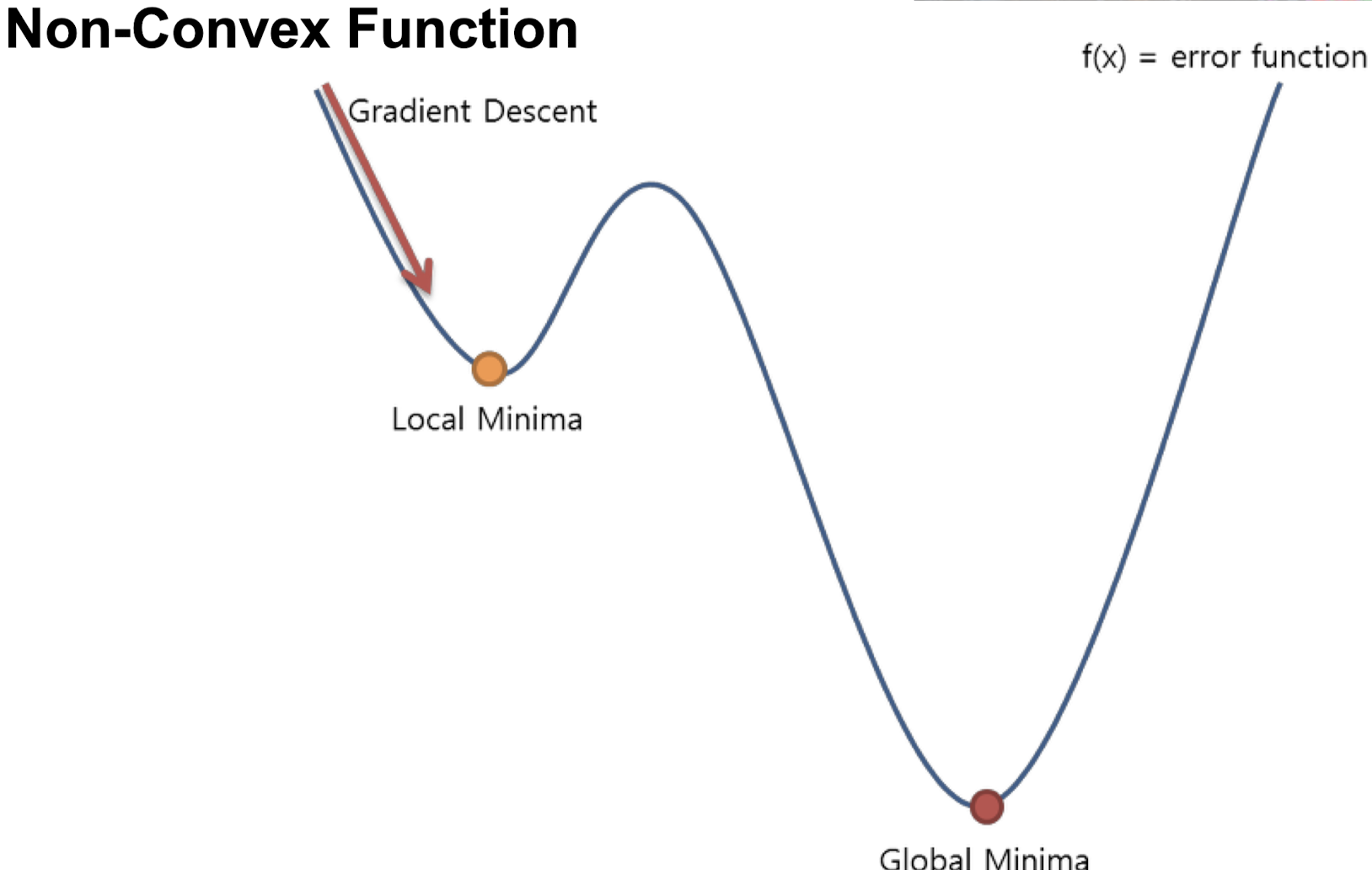
Limitation of gradient descent
Gradient descent는 오직 convex한 경우에만 적용 가능하다.
우린 지금 cost가 0이 되는 경우를 찾아야 한다.
코스트 값은 양수만 나오니 그래프의 모양은 당연히 직선이 아닌 곡선 형태를 띈다.
그런데 만약 그래프가 non-convex의 형태라면?
위의 그림에서 볼 수 있듯 Local minima라는 곳에 안착하게 된다.
cost는 0이 되니 프로그램 상에서는 "아! 여기가 끝이구나!" 라고 생각하게 되는 것이다.
이부분을 한계라고 할 수 있겠다.
LR?
위에서 높을수록 값이 튀고 낮을수록 최소 cost를 찾는데 오랜 시간이 걸린다. 이부분은 뒤에서 마저 ... 라고 언급한 부분이 있다.
이게 무슨 말이냐?! 하면
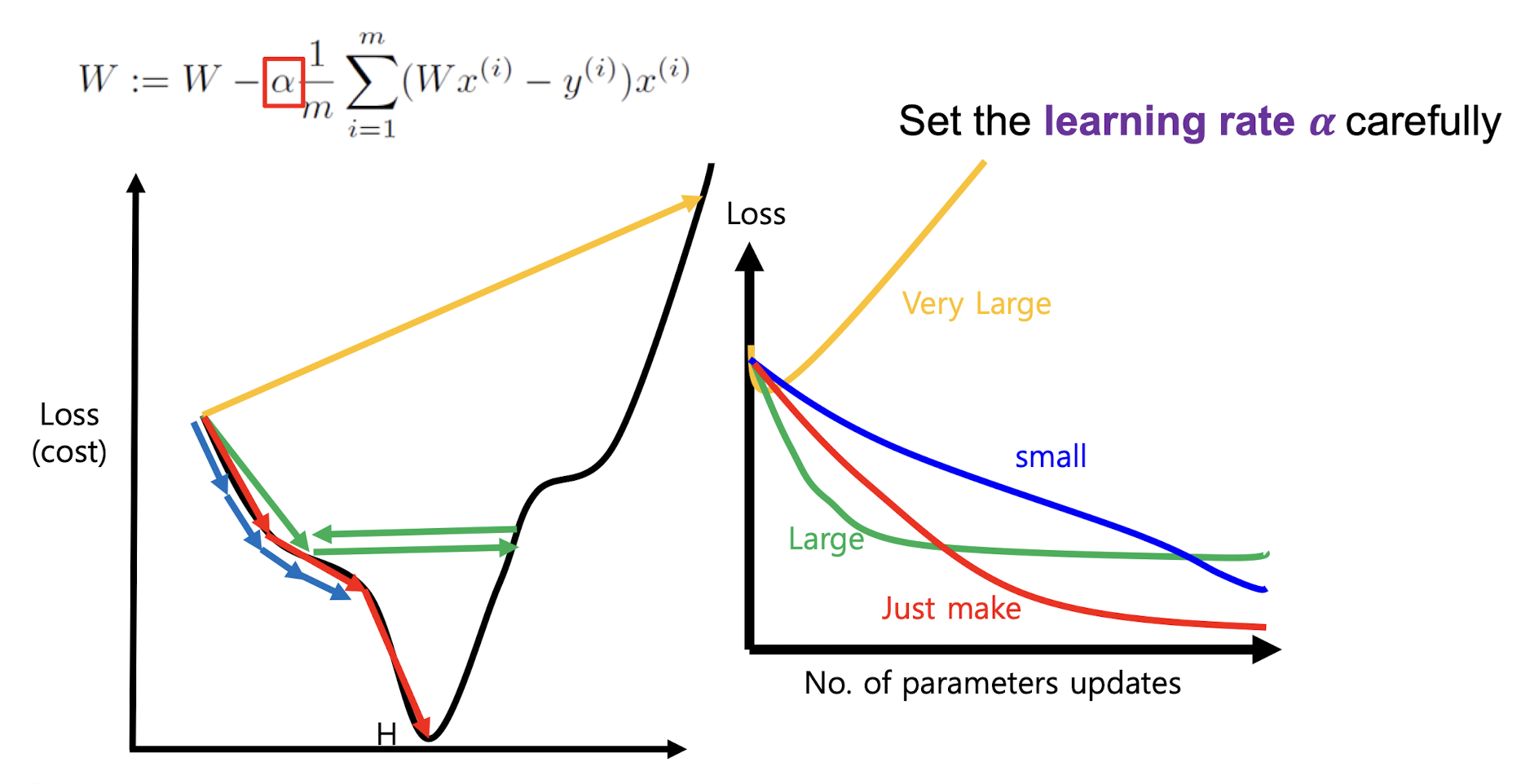
이런 현상이 발생할 수 있다는 의미이다.
알파값이 너무 크면 노란색 화살표 또는 초록색 화살표 처럼 오히려 로스가 커지게 된다.
그렇다고 해서 알파가 너무 작아져버린다면 파란색 화살표 같은 결과가 발생하게 된다.
너무 느리게 학습이 진행된다는 의미이다.
그렇다면 우린 적당한 알파값을 설정해 빨간색 화살표를 찾아내는게 목표가 되겠다.
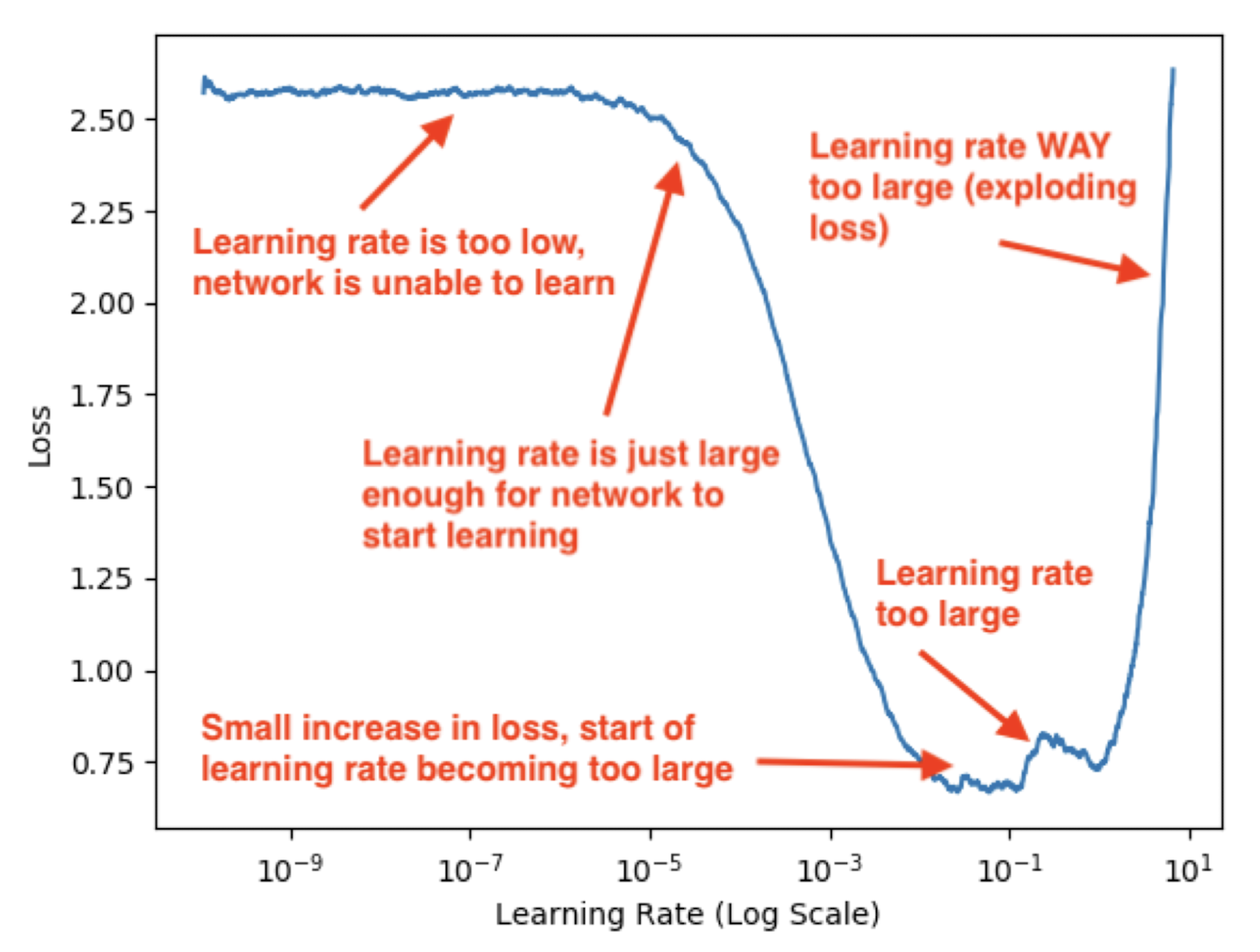
최적의 Learning rate를 찾아내는 그래프이다.
걱정할필요 없다. 이거 다 ~~~ 코드상에서 자동화할 수 있다 ㅎㅎ
하지만 난 코드 구현 부분은 다루진 않을 것이다.
결론
cost function은 hypothesis가 정확한지 확인하고, cost를 최소화하는게 목표이다. 긔록 gradient descent는 cost function 최적화 방법이다(minimization)
LR 이 너무 크면 exploding loss가 일어나고 작으면 network is unable to learn이 일어난다.
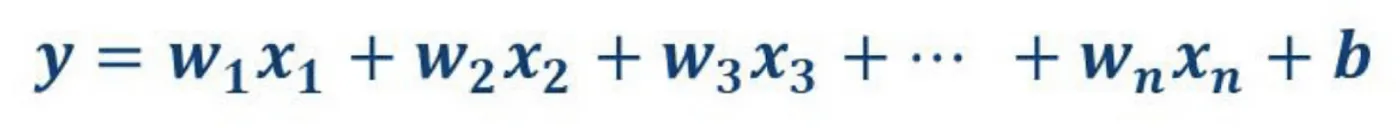
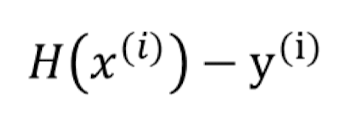
.jpeg)