JPS in Python에서 Python으로 우선 구현해보았으니, 이번엔 JPS 알고리즘을 C++로도 작성해보려고 한다.

C++ 구현 로드맵

목표

• Python 코드의 모든 주요 요소를 C++로 변환하여 구현하기!
• 점프 함수와 JPS 함수에서 Python의 논리를 그대로 가져오되, C++의 자료 구조와 문법에 맞게 변환하기!

Python에서 C++로 재구현할 때 핵심

Python과 C++은 문법과 자료 구조가 다르기 때문에, Python 코드를 만들 때 이러한 요소는 C++에 맞게 변환해야 한다.

1. 데이터 타입 지정
   • Python은 동적 타입, C++은 정적 타입을 사용한다.
   • ex) Python의 list는 C++에서 std::vector로 변환
2. 표준 라이브러리 활용
   • Python의 heapq는 C++의 std::priority_queue로 대체
   • Python의 dict는 C++의 std::unordered_map으로 대체
3. 함수 정의와 호출
   • Python의 함수 정의 방식은 C++의 return_type function_name(parameters)로 변경
4. 루프 및 조건문
   • Python의 for, while 루프를 C++에 맞게 변환
5. 템플릿 및 자료구조
   • C++에서 std::pair, std::vector 와 같은 템플릿을 활용

---

코드 작성

1. 주요 헤더 파일

#include <iostream>
#include <vector>
#include <queue>
#include <cmath>
#include <unordered_map>

각 헤더 파일의 역할

1. <iostream> : 표준 입출력
2. <vector> : Python의 list와 비슷한, C++의 동적 배열 자료구조
3. <queue> : 우선순위 큐 priority_queue를 사용하기 위함
4. <cmath> : 휴리스틱 함수 구현을 위함 (sqrt, pow)
5. <unordered_map> : Python의 dict에 해당하며, 키-값 쌍을 저장

2. 휴리스틱 함수

double heuristic(pair<int, int> node1, pair<int, int> node2) {
    int x1 = node1.first, y1 = node1.second;
    int x2 = node2.first, y2 = node2.second;
    return sqrt(pow(x1 - x2, 2) + pow(y1 - y2, 2));
}

• 두 점 사이의 직선 거리를 유클리드 거리로 계산
• JPS에서 $f(n) = g(n) + h(n)$에 사용되는 $h(n)$ 값

3. 점프 함수

JPS의 핵심 로직, 특정 방향으로 점프하면서 강제 점프 포인트를 탐지

pair<int, int> jump(const vector<vector<int>>& grid, pair<int, int> current, pair<int, int> direction, pair<int, int> goal){
    int x = current.first, y = current.second;
    int dx = direction.first, dy = direction.second;

    while (true) {
        x += dx;
        y += dy;

        if (x < 0 || y < 0 || x >= grid.size() || y >= grid[0].size || grid[x][y] == 1) {
            return {-1, -1}; // 장애물 또는 경계
        }

        if (make_pair(x, y) == goal) {
            return {x, y}; // 목표에 도달
        }

        if (dx != 0 && dy != 0) { // 대각선 이동
            if ((grid[x - dx][y] == 1 grid[x][y - dy] == 0) || grid[x][y - dy] == 1 && grid[x - dx][y] == 0) {
                return {x, y};
            }
        } else if (dx != 0) { // 수평 이동
            if ((y > 0 && grid[x][y - 1] == 1) || (y < grid[0].size() - 1 && grid[x][y + 1] == 1)) {
                return {x, y};
            }
        } else if (dy != 0) { // 수직 이동
            if ((x > 0 && grid[x - 1][y] == 1) || (x < grid.size() - 1 && grid[x + 1][y] == 1)) {
                return {x, y};
            }
        }

        if (dx != 0 && dy != 0) { // 대각선 이동 중
            auto next_jump_x = jump(grid, {x, y}, {dx, 0}, goal);
            auto next_jump_y = jump(grid, {x, y}, {0, dy}, goal);
            if (next_jump_x.first != -1 || next_jump_y.first != -1) {
                return {x, y};
            }
        }
    }
}

동작 방식

1. (x, y)를 주어진 방향으로 이동
   • dx와 dy를 더하면서 한 칸씩 이동
2. 경계 및 장애물 체크
   • 경계나 장애물에 도달하면 {-1, -1} 반환
3. 목표 지점 탐지
   • (x, y)가 목표 지점과 동일하면 반환
4. 강제 점프 포인트 탐지
   • 장애물 때문에 경로를 바꿔야 한다면 (x, y) 반환
5. 대각선 이동
   • 수평/수직 방향으로 추가 점프를 시도하며 강제 점프 포인트 탐지

+) 수정 사항
jump 함수의 대각선 탐색 부분을 다음과 같이 변경했다.
복잡한 맵에서 테스트해보니 대각선 방향으로 이어서 배치된 장애물을 통과하는 현상이 있었기에, 이를 수정했다.

// === 대각선 이동 중 추가 점프 ===
        if (dx != 0 && dy != 0) {
            // 수평 및 수직 경로가 모두 유효한지 검사
            if (grid[x - dx][y] == 1 && grid[x][y - dy] == 1) {
                return {-1, -1}; // 대각선 이동 불가
            }

            // 수평 또는 수직 방향의 점프 포인트 확인
            auto next_jump_x = jump(grid, {x, y}, {dx, 0}, goal);
            auto next_jump_y = jump(grid, {x, y}, {0, dy}, goal);

            if (next_jump_x.first != -1 || next_jump_y.first != -1) {
                return {x, y};
            }
        }

4. JPS 탐색 함수

전체 JPS 탐색을 수행하며 최단 경로를 반환한다.

vector<pair<int, int>> jps(const vector<vector<int>>& grid, pair<int, int> start, pair<int, int> goal) {
    // 우선순위 큐 정의
    priority_queue<tuple<double, double, pair<int, int>>, vector<tuple<double, double, pair<int, int>>>, greater<>> open_set;

    // 경로 추적용 딕셔너리
    unordered_map<pair<int, int>, pair<int, int>, pair_hash> came_from;

    // g(n) 비용 저장용 딕셔너리
    unordered_map<pair<int, int>, double, pair_hash> g_costs;

    // 탐색 방향 정의
    vector<pair<int, int>> directions = {
        {-1, 0}, {1, 0},  // 위, 아래
        {0, -1}, {0, 1},  // 왼쪽, 오른쪽
        {-1, -1}, {1, 1}, // 왼쪽 위, 오른쪽 아래
        {-1, 1}, {1, -1}  // 오른쪽 위, 왼쪽 아래
    };

    // 시작 지점 초기화
    open_set.push({0 + heuristic(start, goal), 0, start});
    g_costs[start] = 0;

    while (!open_set.empty()) {
        auto [_, g, current] = open_set.top();
        open_set.pop();

        // === 목표 지점 도달 시 경로 반환 ===
        if (current == goal) {
            vector<pair<int, int>> path;
            while (came_from.find(current) != came_from.end()) {
                path.push_back(current);
                current = came_from[current];
            }
            path.push_back(start);
            reverse(path.begin(), path.end());
            return path;
        }

        // === 모든 방향 탐색 ===
        for (const auto& direction : directions) {
            auto jump_point = jump(grid, current, direction, goal);
            if (jump_point.first != -1) {
                double tentative_g = g + heuristic(current, jump_point);

                if (g_costs.find(jump_point) == g_costs.end() || tentative_g < g_costs[jump_point]) {
                    g_costs[jump_point] = tentative_g;
                    double f = tentative_g + heuristic(jump_point, goal);
                    open_set.push({f, tentative_g, jump_point});
                    came_from[jump_point] = current;
                }
            }
        }
    }

    return {}; // 경로를 찾을 수 없는 경우
}

동작 방식

1. 우선순위 큐 사용
   • Python의 heapq에 해당
   • f = g + h 값을 기준으로 가장 작은 비용의 점을 먼저 처리
2. came_from 와 g_costs 관리
   • came_from : 각 점으로 어떻게 도달했는지 기록
   • g_costs : 특정 점까지의 비용 ($g(n)$) 기록
3. 목표 지점 도달시 경로 생성
   • came_from을 따라 경로 역추적하여 반환
4. 각 방향 탐색
   • jump 함수로 강제 점프 포인트를 탐지하고, 새 점프 포인트를 큐에 추가

5. 메인 함수

int main() {
    // 맵 정의 (0 : 이동 가능, 1 : 장애물)
    vector<vector<int>> grid = {
        {0, 0, 0, 0, 0},
        {0, 1, 1, 1, 0},
        {0, 0, 0, 1, 0},
        {0, 1, 0, 0, 0},
        {0, 0, 0, 0, 0}
    };

    pair<int, int> start = {0, 0};
    pair<int, int> goal = {4, 4};

    auto path = jps(grid, start, goal);

    if (!path.empty()) {
        cout << "최단 경로 : ";
        for (const auto& p : path) {
            cout << "(" << p.first << ", " << p.second << ") ";
        }
        cout << endl;
    } else {
        cout << "경로를 찾을 수 없습니다." << endl;
    }

    return 0;
}

6. (추가) 사용자 정의 해시함수

A* in C++에서와 마찬가지로, std::unordered_map에서 std::pair<int, int>를 키로 사용하려면, 이를 위한 사용자 정의 해시 함수가 필요하다.

struct pair_hash {
    template <class T1, class T2>
    size_t operator()(const pair<T1, T2>& p) const {
        auto h1 = hash<T1>{}(p.first);
        auto h2 = hash<T2>{}(p.second);
        return h1 ^ (h2 << 1); // XOR 연산으로 해시 값 결합
    }
};

---

실행 결과

최단 경로 : (0, 0) (1, 0) (2, 1) (3, 2) (3, 3) (4, 4)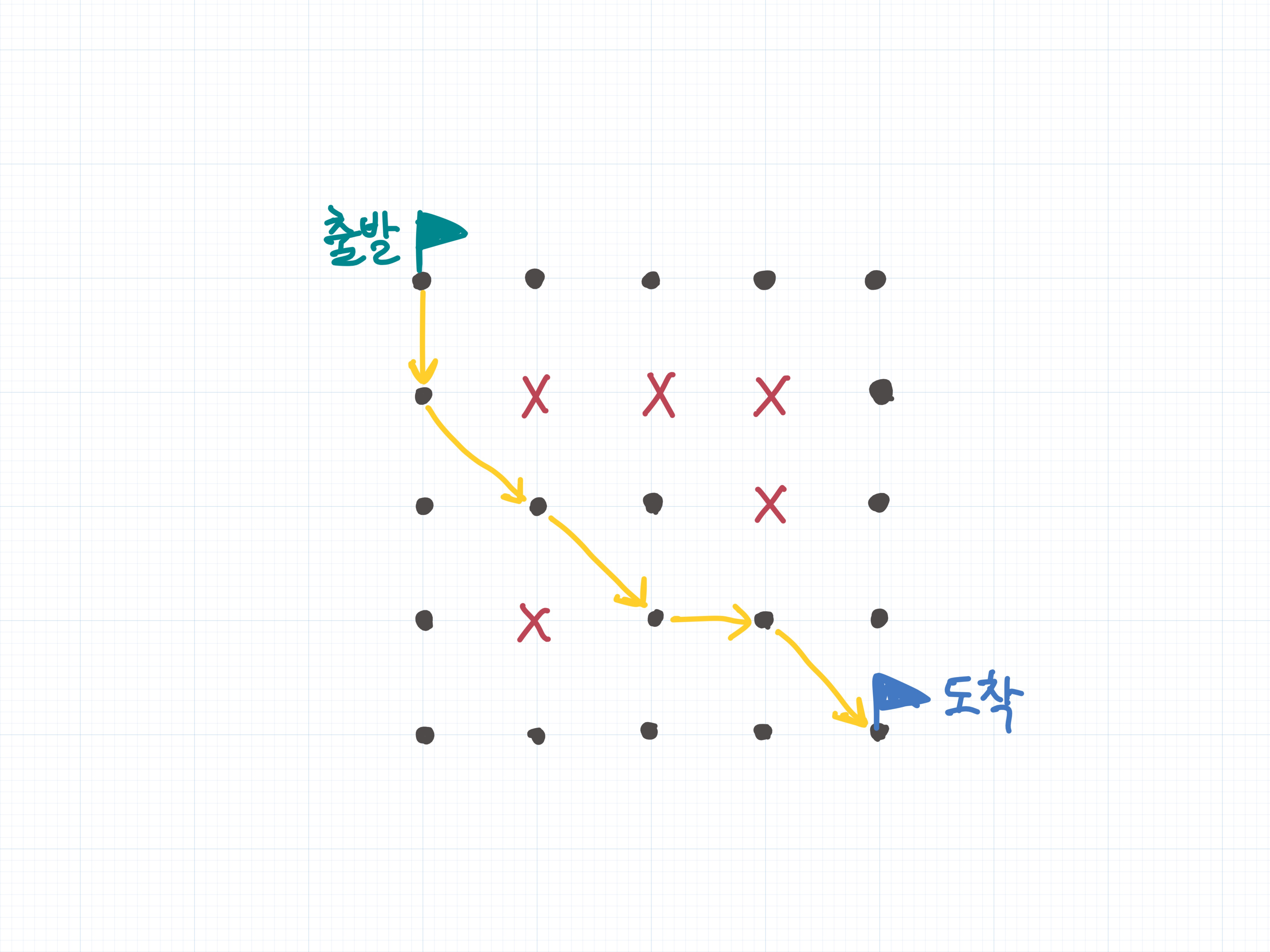 

전체 코드는 Github : https://github.com/leemsia/Pathfinding_Algorithms