여태까지 했던 주제(Informer TFT)와 매우 상반되는 주제이다.
사실 이전까지 했던 Transformer 기반의 TimeSeriesForecasting은 Attention에 기반을 두면서, LTSF에 강점이 있었다.
이번 포스팅에서는 이러한 기존의 Transformer 기반에 맞춰져 있던 TimeSeries Forecasting에 대한 관점을 어떻게 바꿨을지를 확인하면서 보면 좋을 것 같다.

이 논문의 난이도는 직관적으로 이해가 가도록 구성해놔서 이해하기 좋았다.

Abstract

최근에, LTSF task를 위한 많은 Transformer 기반에 모델들이 나왔다
과거 몇 년 동안에 Performance 향상에도 불구하고 우리는 이 work에 대한 연구들이 과연 진짜 효과가 있는지 질문을 던진다
구체적으로, Transformers는 틀림없이(arguably) long sequence에서 의미적인 상관관계를 추출하기 위해 가장 성공적인 solution이다 하지만, time-series modeling에서 우리는 연속적인 포인트들의 순서집합에서 temporal relation을 추출한다.

Positional encoding을 employing하고 transformers에서 sub series를 embed 한 토큰들을 상용하는 것은 몇 가지 순서 정보 보존을 가능케 하는 반면에, 순서를 고려하지 않는 (Permutation-Invariant) self-attention mechanism의 속성은 필연적으로(inevitably) temporal information loss를 일으킨다.

우리 주장의 유효성을 보이기 위해서 우리는 LTSF-Linear이라고 불리는 비교를 위한 simple one-layer linear models의 집합을 소개한다
9가지의 실생활 데이터에서 우리의 LTSF-Linear은 복잡한 transformer기반의 LTSF모델들 보다 훌륭한 성능을 냈고 몇몇은 큰 차이(20%~50%)가 났다
더욱이, 우리는 LTSF모델의 다양한 구성요소들이 그들의 temporal relation 추출능력에 미치는 영향을 알아보기 위해서 포괄적이고 경험적인 studies를 수행한다
우리는 이런 놀라운 발견이 LTSF task에 대해서 새로운 연구 방향을 열어주길 기대한다

Introduction

Time series는 ubiquitous하다 오늘날의 data-driven world에서 주어진 historical data에서 time series forecasting(TSF)는 다양한 분야에서 적용할 수 있는 long-standing task이다
Example> traffic flow estimation, energy management, financial investment
과거 몇 십년간 TSF solution 들은 traditional statistical methods(e.g. ARIMA)와 machine learning techniques(e.g. GBRT) 로부터 deep learning-based solutions(e.g. Recurrent Neural Net-works, Temporal Convolutional Networks)로의 Progression을 겪었다
Transformer는 NLP, speech recognition, computer vision등 다양한 분야에서 뛰어난 성능을 보여주면서 틀림없이 가장 성공적인 sequence modeling architecture로 자리매김했다
최근에 time series analysis에 대해 transformer base solutions가 많이 나왔다
Most notable models

• LogTrans [16] (NeurIPS 2019),
• Informer [30] (AAAI 2021 Best paper),
• Autoformer [28] (NeurIPS 2021),
• Pyraformer [18] (ICLR 2022 Oral),
• Triformer [5] (IJCAI 2022)
• FEDformer [31] (ICML 2022)

Transformers의 main working power는 multi-head self-attention mechanism으로부터 온다 이는 long sequence에서 요소들 간에 의미적인 상관관계를 뽑아내는 능력이 우수 하다
하지만 self-attention은 permutation-invariant하다. 다양한 type의 positional encoding techniques를 사용하는 것은 몇몇 순서정보를 보존할 수 있는 반면에 self-attention을 적용한 이후에 몇몇 temporal information loss는 필연적으로 발생한다
이는 NLP와 같은 의미가 풍부한 application에 대해서는 그리 심각한 문제가 아니다
(e.g. the semantic meaning of a sentence is largely preserved even if we reorder some words in it)
하지만, time series data를 분석할 때는 많은 데이터에서 그 자체로 주로 의미가 부재한다. 그리고 우리는 연속적인 points 사이에서 temporal changes를 모델링 하는데 관심이 있다.
다시 말하자면 NLP와 달리 순서 그 자체가 time series에서는 critical한 역할을 한다
결과적으로, 우리는 다음의 intriguing(흥미로운) 질문에 마주한다:
Are Transformers really effective for long-term time series forecasting?
더욱이, 존재하는 Transformer기반의 LTSF solutions는 그들의 실험에 있는 traditional method보다 뛰어난 예측 정확도 향상을 보였다.
모든 비교대상(non-transformer)는 autoregressive 또는 iterated multi-step(IMS) forecasting방식을 사용했다 이는 LTSF문제에 대해 significant error accumulation effect로부터 발생했다. 따라서 이번 paper에서 우리는 transformer 기반의 LTSF solution과 direct multi-step(DMS) forecasting strategies의 진짜 성능을 확인하기 위해 도전한다

Not all time series are predictable, let alone long-term forecasting (e.g., for chaotic systems).
우리는 long-term forecasting이 상대적으로 trend와 periodicity가 명확한 time-series에 대해 알맞다고 가정한다
Linear model들은 이미 이러한 정보를 추출할 수 있기 때문에, 우리는 비교를 위한 새로운 baseline으로써 LTSF-Linear로 불리는 간단한 모델을 소개한다
LTSF-Linear은 미래의 time series를 직접적으로 forecast하기 위해서 과거의 time series를 하나의 layer를 갖는 linear모델과 함께 선형회귀를 한다

우리는 기존의 transformers에 주장과 달리 그들의 대부분이 long sequences로부터 temporal relation을 추출하는데 실패한 것을 확인했다
(i.e. the forecasting errors are not reduced(sometimes even increased) with the increase of look-back window sizes)-> 참고하는 과거 데이터의 수를 늘렸는데 forecasting error가 줄어들기는 커녕 늘어나기도 했음
마침내, 우리는 다양한 Ablation studies를 그들 안에 있는 다양한 design elements의 영향을 연구하기 위해서 현재 존재하는 transformer base의 TSF solutions 에 수행했다

Contributions

• LTSF task에서 Transformer boom에 도전하는 첫번째 work임
• 우리의 주장을 확인하기 위해서 매우 간단한 linear model인 LTSF-linear을 소개하고 우리는 transformer 기반의 LTSF solution을 9개의 bench-marks에 대해 비교한다
  LTSF-Linear은 LTSF problem에 대해 새로운 기준이 된다
• 우리는 포괄적이고 경험적인 study들을 이미 존재하는 transformer 기반의 solution에 여러 측면에 대해 ablation study를 수행한다,

1. Long inputs을 모델링 하는 것의 능력
2. Time series order의 민감도
3. Positional encoding과 sub-series embedding의 영향
4. 효과적인 비교
   이러한 발견들은 이 분야의 미래 연구에 대해 benefit이 될 것이다

위의 기여들과 함께
우리는 time series에 대한 적어도 현재 존재하는 LTSF를 위한transformer의 temporal modeling 능력들이 과장됐다고 결론 내렸다
동시에 LTSF-Linear가 더 좋은 prediction accuracy를 갖음을 알았다, 그것은 단순히 long term time series forecasting 문제의 challenging에 미래 연구분야에 대한 단순한 baseline을 제공한다

Preliminaries: TSF Problem Formulation

C개의 변수들을 포함하는 time series에대해, 주어진 historical data $χ=$$\{X_1^t,..,X_C^t\}$$_{(t=1)}^L$, where L is the look-back window size and $X_i^t$ 는 i 번째 변수의 t time step을 의미한다.
Time series forecasting 은 다음을 예측하는 것이다 다음은 T future time steps에 대한 value이다
$\hat χ=$$\{\hat X_1^t,..,\hat X_C^t\}$$_{(t=L+1)}^{L+T}$
T>1일 때, iterated multi-step(IMS) forecasting을 적용하는 모델은 single-step을 forecasting하고 그 값을 multi-step prediction을 얻기 위해서 적용한다.
대안으로 direct multi-step(DMS) forecasting은 직접적으로 multi step forecasting 객체를 한번에 최적화한다
DMS forecasting 결과와 비교해서 IMS prediction 값들은 autoregressive한 추정 절차 덕분에 더 작은 분산을 갖지만 그들은 필연적으로 error accumulation effects가 생긴다

결과적으로, IMS forecasting은 높은 정확도를 갖는 single-step forecaster가 있고 예측범위가 짧을 때 선호된다.(예측범위가 짧으면 error accumulation effects가 줄어들기 때문에)
이와 반대로, DMS forecasting은 unbiased한 single-step forecasting model을 얻기 어렵거나 예측범위가 클 때 더 정확한 예측을 생성한다

Transformer-Based LTSF Solutions

Transformer기반의 모델들은 multi-head self-attention의 효용성 덕분에 NLP와 Vision과 같은 많은 AI task에서 높은 성능을 달성했다. 이는 Transformer기반의 time-series modeling에 많은 연구가 이뤄지게 되는 역할을 했다. 특히, 많은 연구가 LTSF task에 노력을 기울였다
Transformer model이 워낙 Long-range dependency를 잘 Capture하기 때문에 그들의 대부분은 덜연구된 long-term forecasting problem에 집중했다(T>>1)
Vanilla Transformer를 LTSF task에 적용하면 quadratic한 time/memory complexity와 autoregressive decoder design에 의해서 error accumulation이 생겼고 이 문제를 극복한 모델이 Informer라는 모델이다
그 이후에 더 많은 Transformer variants(변형체)은 performance나 모델의 효율성을 향상시키기 위해서 다양한 time series features을 그들의 모델안으로 도입한다
우리는 존재하는 Transformer 기반의 LTSF solution들을 figure 1에 요약했다.

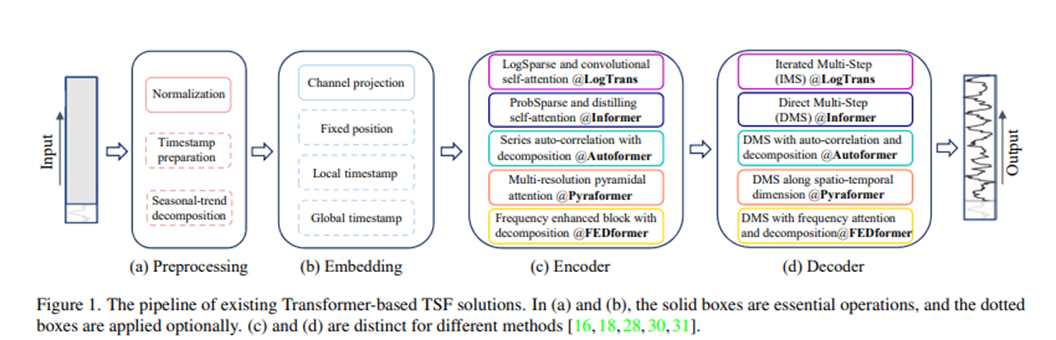
게다가, Autoformer는 처음으로 seasonal-trend decomposition을 각각의 neural block뒤에 적용한다.
seasonal-trend decomposition은 time series analysis에서 raw data를 더욱 predictable 하게 만드는 standard method이다. 구체적으로, 그들은 moving average kernel을 input sequence에 Trend-Cyclical component를 추출하기 위해서 사용한다.
Original sequence와 Trend component의 차이는 seasonal component에 의존한다.
FEDformer는 다양한 kernel size를 가진 moving average kernel에 의해 추출된 trend components를 혼합하기 위해서 전문가 의견과의 혼합을 제안한다

Input embedding strategies: Transformer에서 self-attention layer는 time series의 positional information을 보존할 수 없다.
하지만 local positional information(i.e. time series의 순서)는 중요하다.
게다가 계층적인(hierarchical) timestamps(week, month, year)과 agnostic timestamps(holidays and events)와 같은 global temporal information 또한 유익하다.
Time-series inputs의 temporal context를 강화하기 위해서, SOTA transformer based methods에서 실용적인 design은 몇 가지 embedding들을 추가한다(e.g. fixed positional encoding[Transformer], channel projection embedding[informer], input sequence안에 learnable temporal embeddings[informer])
더욱이, temporal convolution layer또는 learnable time-stamps와 함께한 temporal embeddings이 소개됐다

self-attention schemes

Self-attention schemes: Transformer는 paired elements사이에 의미적인 의존성을 추출하기 위해서 self-attention mechanism에 의존한다
Vanilla transformer의 Quadratic한 time and memory complexity를 줄임으로써, 최근에 works는 효율성에 대한 두가지 전략을 제안한다.
1. LogTrans 와 Pyraformer에서는 명시적으로 self-attention scheme 안에 Sparsity bias를 소개한다, LogTrans는 computational complexity를 O(LlogL)로 줄이기 위해서 Logsparse mask를 사용한다 반면에 Pyraformer는 O(L)수준의 time and memory complexity와 함께 계층적으로 multi-scale을 갖는 temporal dependencies를 잘 capture하기 위해서 pyramidal attention 채택한다
2. Informer와 FEDformer는 low-rank property를 self-attention matrix에서 사용한다 Informer는 Complexity를 O(LlogL)로 낮추기 위해서 ProbSparse self-attention과 self-attention distilling operation을 제안한다 그리고 FEDformer는 Fourier enhanced block과 wavelet enhanced block을 Random selection과 함께 디자인하여 O(L)의 complexity를 달성했다
최근에, Autoformer는 original self-attention layer를 대체하기 위해서 series-wise auto-correlation mechanism을 디자인 한다

Decoder

Decoders: Vanilla Transformer decoder는 autoregressive한 방법으로 sequence의 output을 낸다 이는 slow inference speed 와 error accumulation effects를 갖는다, especially for long-term predictions
Informer는 DMS forecasting을 위한 generative-style decoder를 디자인한다. 다른 변형된Transformer도 비슷한 DMS strategies를 사용한다.
예를 들어 Pyraformer는 Spatio-temporal axes로 concatenating한 fully-connected layer를 decoder로써 사용한다
Autoformer는 두가지 trend-cyclical components 와 stacked 된 auto-correlation mechanism 으로부터 구해진 seasonal components를 final prediction을 얻기 위해 더한다
FEDformer는 final results를 decode하기 위해 제안된 frequency attention block과 함께 decomposition scheme을 사용한다
Transformer 모델들의 전제는 paired elements사이에 의미적인 상관관계가 있다는 것이다 그리고 self-attention mechanism은 그 자체로 순서를 고려하지 않고 Transformer models의 temporal relations modeling 능력은 input tokens와 관계된 positional encodings에 크게 의존한다
Time series안에 있는 raw 수치 데이터를 고려하면(e.g. stock prices or electricity values), There are hardly any point-wise semantic correlations between them.
Time series modeling에서 우리는 주로 point들 사이에 temporal relation에 흥미가 있다 그리고 짝지어진 관계 대신에 이들 구성요소의 순서는 중요한 역할을 한다
Positional encoding과 sub-series가 embedding된 tokens를 사용하는 것은 몇몇 ordering information의 보존을 가능케하는 반면에, self-attention에 순서를 고려하지 않는 속성은 필연적으로 temporal information loss를 일으킨다
위와 같은 관찰 때문에 우리는 Transformer base의 LTSF solution의 효용성을 revisit(재고하다)하는 것에 관심이 있다

Embarrassingly simple Baseline

이미 존재하는 Transformer 기반의 LTSF solution(T>>1)들의 실험에서 모든 비교되는 baseline(non-Transformer)들은 IMS forecasting technique들을 사용한다, 이들은 이미 error accumulation effects로부터 큰 영향을 받는 것으로 알려졌다
우리는 Transformer 기반의 solution들의 성능향상은 그 solution들에게 쓰이는 DMS strategy때문이라고 가정한다 -> (내 생각) 이게 동기가 돼서 그럴 바엔 그냥 Linear regression을 써버리자!

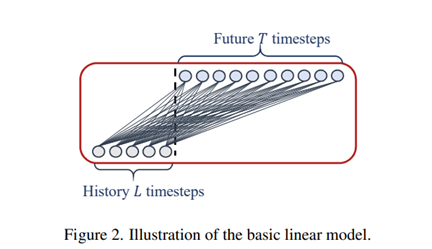
우리는이 가정을 확인하기위해서, 비교하기 위한 baseline으로써 temporal linear layer를 통해 LTSF-Linear이라고 불리는 가장 간단한 DMS model을 만들 것이다
LTSF-Linear의 기본이 되는 방정식은 직접적으로 future prediction에 대한 historical time series를 weighted sum operation을 통해 회귀를 진행한다

Mathematical expression
$\hat X_i=WX_i$, Where $W∈R^{T×L}$
W는 temporal axis를 따른 linear layer이다 $\hat X_i$와 $X_i$은 각각의 i번째 variates에 대한 prediction과 input이다

Note>
LTSF-Linear은 여러 variates에 걸쳐서 weights를 share하고, 어떠한 spatial correlations도 모델링 하지 않는다(spatial correlations=variate간의 relation?)
LTSF-Linear은 linear models의 집합이다. Vanilla Linear은 하나의 layer를 갖는 linear model이다. 다른 영역(e.g. finance, traffic, and energy domains)에 걸쳐 Time series를 핸들링하기 위해서, 우리는 두가지 preprocessing methods와 함께 두가지 변형(DLinear, NLinear)을 소개한다

DLinear

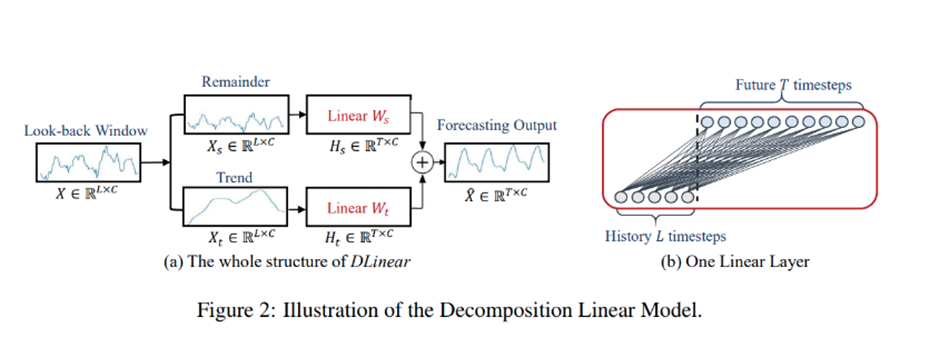
구체적으로, DLinear은 Autoformer과 FEDformer에서 사용하는 Decomposition scheme과 linear layers의 결합이다
먼저 raw data input을 moving average kernel에 의해 trend와 remainder(seasonal) component로 decompose 시킨다
그 이후 one-layer linear layers를 각각의 component에 적용한다, 그리고 우리는 예측을 얻기 위해서 두가지의 features를 더한다
명시적으로 trend를 handling 함으로써, Data안에 있는 Trend가 clear 할 때, DLinear은 Vanilla Linear의 성능을 강화한다

NLinear

반면에, LTSF-Linear의 성능을 높이기 위해서, dataset안에 distribution shift가 있을 때, NLinear는 먼저 input을 sequence의 마지막 값으로 뺀다
그 이후, 그 input은 linear layer를 통과하고 그 빠진 부분은 final prediction을 만들기 전에 다시 더해준다
이런 빼고 더하는 과정은 input sequence에 대한 simple normalization이다

Experiments

Experimental settings

Dataset. 우리는 흔하게 사용하는 9개의 real-world datasets에 대해 추가적인 experiments를 수행한다

• ETT (Electricity Transformer Temperature) [30] (ETTh1, ETTh2, ETTm1, ETTm2),
• Traffic,
• electricity,
• Weather,
• ILI,
• Exchange Rate [15].
  위에 모두 multivariate time series이다 우리는 Appendix에 data descriptions를 남겨 놓는다

Evaluation metric. Previous works에 따라, 우리는 MSE와 MAE를 성능을 비교할 core metrics로 사용한다

Compared methods. 우리는 5가지의 Transformer 기반의 methods를 포함한다: FEDformer, Autoformer, Informer, Pyraformer and LogTrans
게다가 우리는 단순한 DMS method도 포함한다: Closest Repeat, 이는 단순히 그냥 look-back window안에 있는 마지막 value를 반복한다
FEDformer의 두가지 변형들이 있기 때문에, 우리는 더 정확한 accuracy를 갖고 있는 FEDformer-f via Fourier transform 와 비교한다

Comparison with Transformers

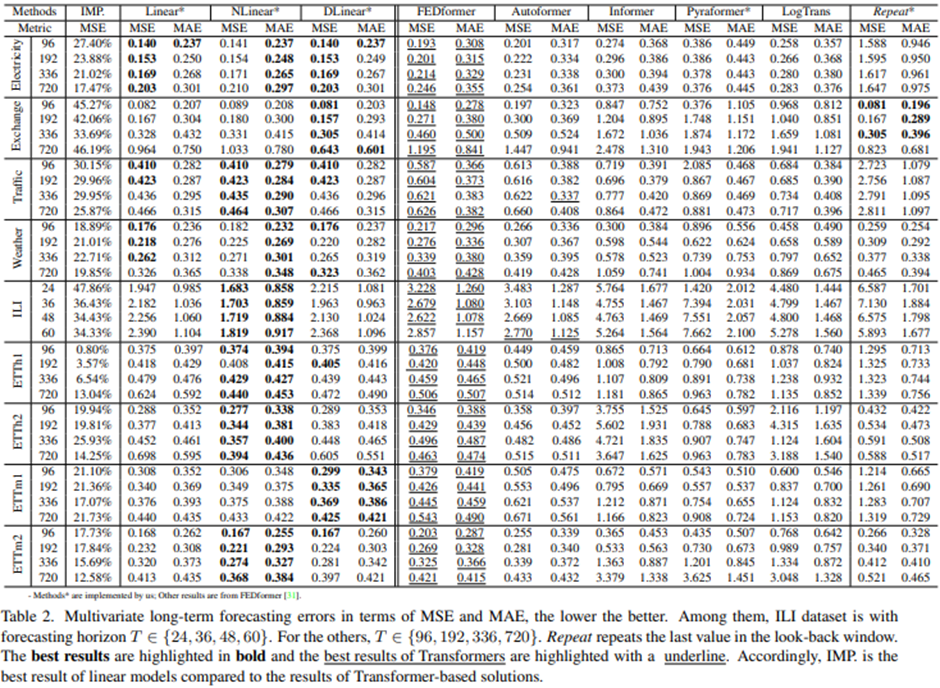
Quantitative results

Quantitative results: Table2에서, 우리는 이전 work의 experimental setting을 따라서 9가지의 실험 데이터에 대해 모든 언급된 transformer들을 평가해 봤다

놀랍게도, LTSF-Linear의 성능은 은 variates 사이에 correlations를 모델링 하지도 않았는데 SOTA인 FEDformer를 대부분의 case에 대해 multivariate forecasting에서 20퍼센트에서 50퍼센트 정도 능가했다

다른 different time series benchmarks에 대해, NLinear과 DLinear은 distribution shift와 trend-seasonality features를 다루는 데에 우월성을 보인다

우리는 또한 ETT datasets으로 univariate forecasting에 대해서도 실험해봤는데 여전히 큰 차이로 LTSF-Linear가 Transformer base의 LTSF solutions 보다 뛰어난 성능을 보인다

FEDformer는 ETTh1에서 경쟁력 있는 forecasting accuracy를 달성했다. 이는 FEDformer가 classical time series analysis techniques(e.g. Frequency processing)를 사용하고 있기 때문에 그렇다, 이는 time series 안에 inductive bias와 temporal feature extraction의 능력을 가지고 왔다

요약하자면 이러한 결과들은 기존에 Transformer기반의 LTSF solutions가 존재하는 9가지의 benchmarks에 대해 효과적이지 않고 반면에 LTSF-Linear은 powerful baseline이 될 수 있다 는 것을 보여준다

다른 흥미로운 관찰할 점은 심지어 naïve Repeat method(Closest Repeat)는 long-term seasonal data(e.g. Electricity and Traffic)을 예측할 때는 나쁜 결과를 보이지만 그것은 놀랍게도 모든 Transformer base method 보다 Exchange-Rate에서 뛰어난 성능을 보인다(around 45%)
환율-> 고려할 data가 많음; 또한 naïve 한 메소드가 잘 먹힐 수 있는 경제관련 지표임

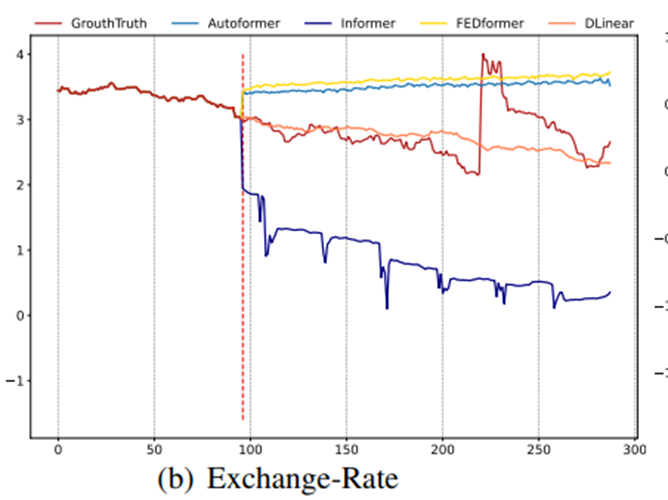
이는 주로 Transformer-based solutions에 잘못된 trend 예측에 의해 발생한다, 이는 training data 안에 있는 갑작스럽게 변화하는 noise들에 모델이 과대적합을 해서 큰 정확도 저하가 발생한 것 같다(see Figure 3(b))
반면에 Repeat은 bias를 갖지 않는다

이것이 DLinear/NLinear가 시계열 특성을 잘 반영하는 이유(모델의 파라미터 개수)

Qualitative results

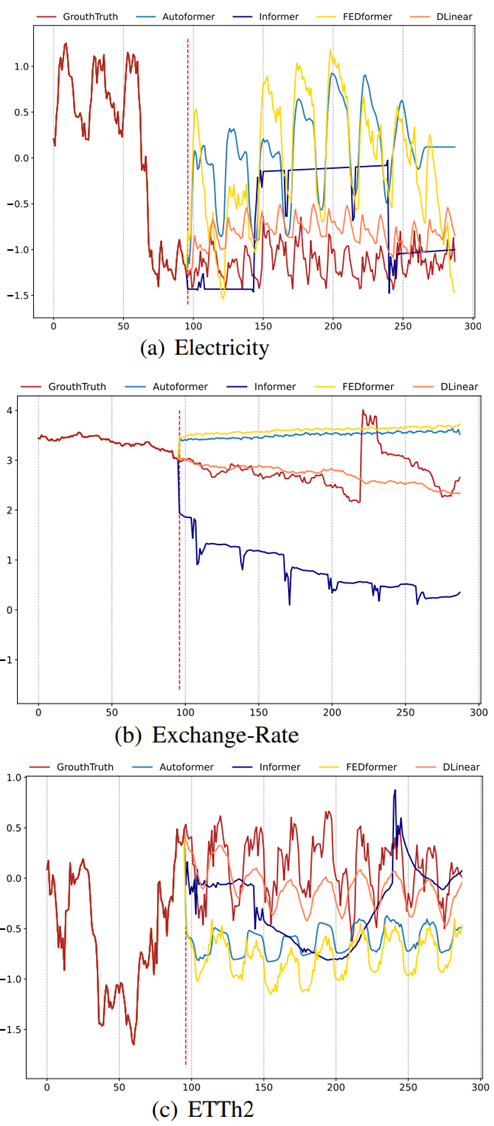
[Input length L=96이고 output length T=192인 모델의 예측 plot]
Fig3에서 보듯이, 우리는 세가지 선택된 Time series datasets에 대해서 Transformer-based solutions와 LTSF-Linear의 예측 결과를 plot 한다:
Electricity (Sequence 1951, Variate 36), Exchange-Rate (Sequence 676, Variate 3), ETTh2 ( Sequence 1241, Variate 2)
위의 dataset들은 다른 temporal patterns를 갖는다

Input length가 96 steps이고 output horizon이 336 steps일 때 Transformer[28,30,31]는 Electricity와 ETTh2에서 future data의 scale과 bias를 잡아내는 데에 실패했다
더욱이 그들은 Exchange-Rate와 같은 비 주기적인 data에서 적절한 trend를 예측하기 어렵다 이런 현상은 LTSF task에 대해 transformer base solution들이 부적절하다는 것을 보여준다.

Ablation Study

More Analyses on LTSF-Transformers

Can existing LTSF-Transformers extract temporal relations well from longer input sequences?

Input data의 개수를 조절

Look-back window size는 우리가 historical data로부터 얼마나 배울 수 있는지를 결정하기 때문에 forecasting accuracy에 크게 영향을 미친다
일반적으로 말하는 점은, 뛰어난 temporal relation extraction 능력을 갖는 더 강력한 TSF model은 look-back window sizes가 커지면 더 좋은 결과를 낼 수 있어야 한다

Input Look-back window 크기의 영향을 알아보기 위해 우리는 input size를 {24, 48, 72, 96, 120, 144, 168, 192, 336, 504, 672, 720} 까지 다양하게 해서 720개의 long term output을 내는 실험을 수행한다
Figure 4는 두가지 데이터셋에 대한 MSE results를 보여준다

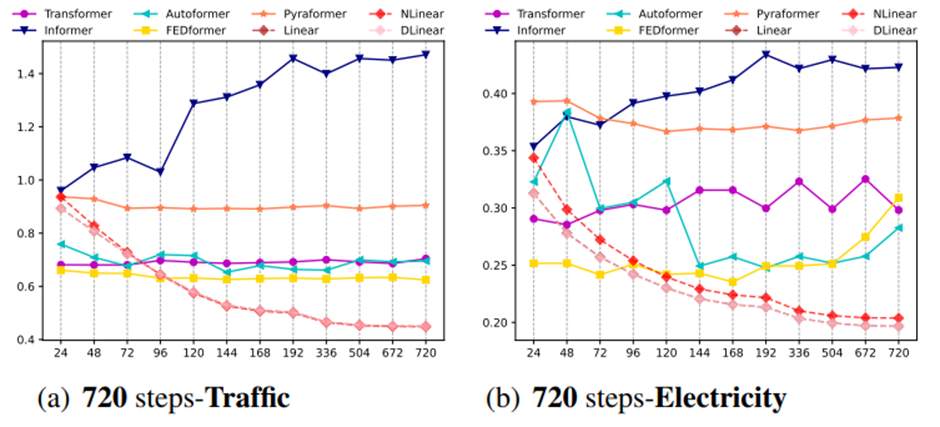
이전 연구들[27,30]로부터 관찰된 것과 비슷하게, existing Transformer-based model의 performance는 악화 되거나 look-back window가 커졌음에도 stable한 상태를 유지한다
대조적으로 모든 LTSF-Linear의 Performances는 look-back window size의 증가와 함께 증가했다.
따라서, 만약 더 긴 sequence가 주어진다면 existing solution들은 temporal information을 추출하는 것 대신에 temporal noises를 overfit하는 경향이 있다
그리고 대부분의 Transformer에 대해서 input size는 96이 정확히 알맞다

What can be learned for long-term forecasting?

→ long-term time series forecasting에서 size는 갖되 바라보는 window의 위치를 다르게 해서 성능을 측정

Look-back window안에 있는 temporal dynamics가 short-term time series forecasting의 forecasting accuracy에 크게 영향을 주는 반면에, 우리는 long-term forecasting은 model이 trend와 periodicity를 잘 capture할 수 있는지에 의존한다고 가정한다
다시 말하자면, forecasting horizon이 더 커질수록 look-back window가 그 자체로 갖는 영향은 줄어든다

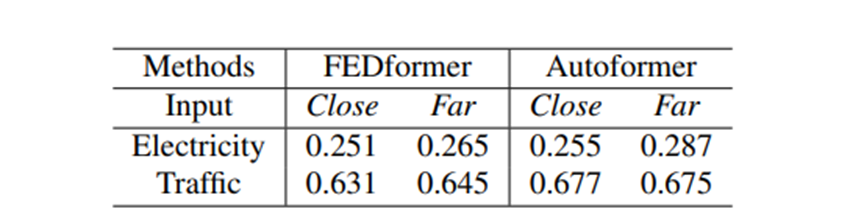
위의 가정을 확인하기 위해서 Table 3에서 우리는 미래의 720 time steps에 대해 두가지의 서로 다른 look-back windows 로부터 forecasting accuracy를 비교한다

(1) The original input L=96 (called Close)
(2) The far input L=96 (called Far) 이는 original 96 step보다 이전 step을 의미한다
Experimental results로부터, SOTA의 성능을 갖는 Transformer의 성능차이가 얼마 나지 않는 것을 볼 수 있다, 이는 이 모델들이 인접한 time series sequence로부터 단순히 비슷한 temporal information을 capture하는 것을 알 수 있다(= window가 close 하건 Far 하건 모델의 성능의 주류는 모델이 trend와 periodicity를 얼마나 잘 캡쳐 할 수 있느냐 에 달려있다)

Dataset의 본래 갖추어진 특징들(periodicity trend)을 capturing하는 것은 일반적으로 많은 수의 parameters가 필요하지 않다.
많은 파라미터들을 사용하는 것은 overfitting을 일으킬 것이다, 이는 왜 LTSF-Linear가 Transformer base methods보다 더 좋은 성능을 내는지에 대한 부분적인 이유이다

Are the self-attention scheme effective for LTSF?

→ Existing solutions안에 들어있는 complex design 들을 빼 보면서 성능 판단

우리는 이런 이미 존재하는 transformer안에 complex designs(e.g. Informer)가 필수적인지 아닌지를 확인한다

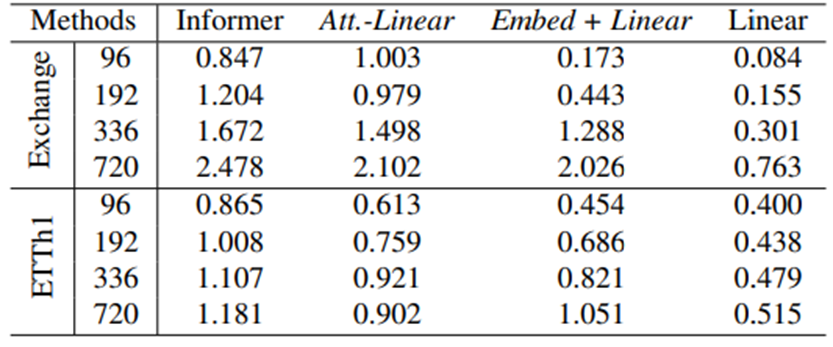
Table4에서, 우리는 점진적으로 Informer에서 Linear로 변화한다.
먼저, 한 self-attention layer를 weights가 dynamically하게 변화하는 fully connected layer로 생각될 수 있기 때문에 우리는 self-attention layer를 linear layer로 대체한다, 이를 Att.-Linear로 부른다.

다음으로, 우리는 Informer에서 embedding layers와 linear layers만 남기기 위해서 informer 안에 있는 다른 보조적인 장치(e.g. FFN) 들을 폐기한다 이를 Embed+ Linear 로 부른다

마지막으로, 우리는 하나의 linear layer로 단순화시킨다. 놀랍게도, Informer의 performance는 적어도 이미 존재하는 LTSF benchmarks에 대해서 simplification이 진행되면서 점점 좋아졌다 이는 self-attention 도식과 다른 복잡한 모듈들의 불필요성을 의미한다

→ 몇 가지 데이터에 대해서만 판단하는 것은 일반화하기에 무리가 있다고 생각함

Can existing LTSF- Transformers preserve temporal order well?

→ Input의 순서를 섞어서 넣어보면서 과연 실제로 existing transformers가 순서를 capture할 수 있는지 확인[얼마나 데미지를 입는지를 통해서]

Self-attention은 내재적으로 순서가 보존되지 않는다(i.e. regardless of the order).
하지만, time series forecasting에서, sequence order는 자주 핵심적인 역할을 한다. 우리는 심지어(even with) positional과 temporal embeddings를 논하지만, 존재하는 Transformer base의 methods는 여전히 temporal information loss의 문제를 갖는다.
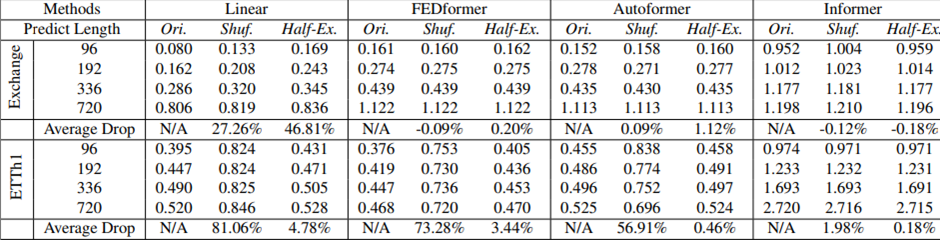
Table 5에서 우리는 embedding strategies 전에 raw input을 섞는다. 두가지 shuffling strategies가 보여진다:
Shuf.는 모든 input sequences를 랜덤하게 섞는다
Half-Ex.는 input sequence의 첫번째 절반을 두번째 절반과 교환한다
흥미롭게도, Exchange Rate에서 심지어 input sequence가 랜덤하게 섞였을 때조차 모든 Transformer 기반의 methods의 성능이 original setting과의 비교에서 변동(fluctuate)되지 않았다. 반대로, LTSF-Liner의 성능은 크게 damage를 입었다.

이는 서로 다른 positional 과 temporal embeddings를 갖는 LTSF-Transformers가 꽤 제한된 temporal relations를 보존하는 것과 LTSF-Transformers가 noisy한 financial data에 과대적합 되는 경향이 있다(be prone to)는 것을 암시한다.
반면에 LTSF-Linear은 적은 파라미터로 과대적합을 피하고 순서가 자연스럽게 모델링 할 수 있다는 것을 암시한다.

ETTh1 dataset에 대해, FEDformer과 Autoformer는 그들의 모델들 안에 있는 time series inductive bias를 소개한다.

이런 time series inductive bias는 dataset이 꽤나 clear한 temporal patterns(e.g. periodicity)를 갖을 때 특정한 temporal information을 추출할 수 있다

따라서 input 데이터의 순서를 완전히 섞었을 때 각각의 성능은 73.28%와 56.91%가 저하되는 것을 볼 수 있다(이는 전체 순서정보를 잃었다고 본다)
추가로, Informer는 여전히 성능저하가 덜한데 이는 temporal inductive bias[Sequential, Temporal Invariance]가 없기 때문이다.
전반적으로 LTSF-Linear의 평균 성능 저하가 Transformer-based methods보다 모든 케이스에서 크다 이는 existing Transformers가 temporal order를 상대적으로 잘 보존하지 않는 것을 의미한다

How effective are different embedding strategies?

→ Embedding을 안 해보면서 Embedding이 얼마나 효과가 있는지 확인

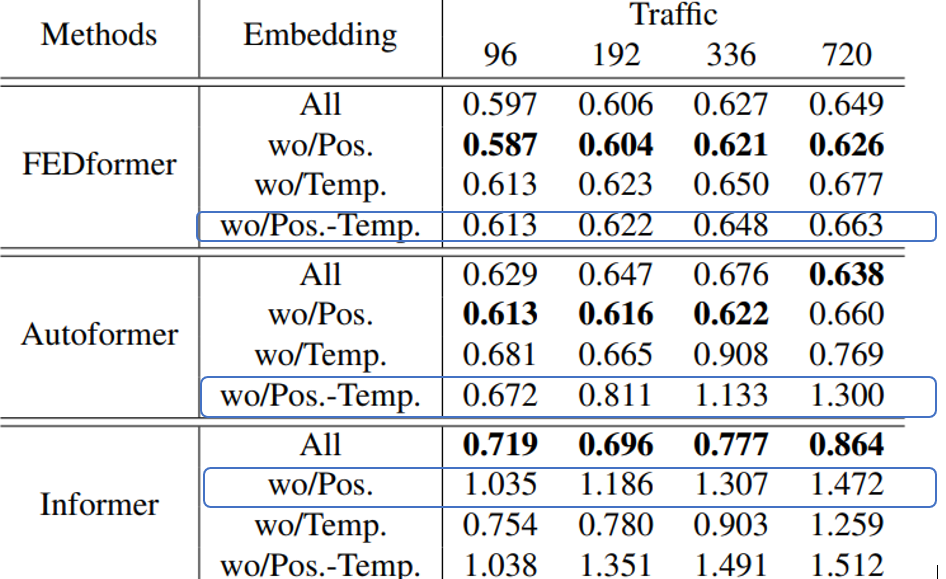
우리는 Transformer-based methods에서 사용하는 position과 timestamp embeddings의 이점을 연구한다.

In Table 6에서 positional embeddings 없이 (wo/Pos) Informer의 forecasting errors는 크게 증가한다.

Timestamp embeddings 없이 (wo/Temp) Informer의 성능은 forecasting lengths가 증가하기 때문에 점진적으로 damage를 입을 것이다.
Informer는 각각의 token에 대해 single time step을 사용하기 때문에 토큰들에 대해 temporal information을 알려줘야 한다

각 토큰에게 single time step을 사용하는 것 대신에, FEDformer와 Autoformer은 temporal information을 embedding하기 위해서 timestamps의 sequence를 입력해준다
그렇기 때문에, 그들은 고정된 positional embedding없이 비교할 만하거나 더 좋은 성능을 이뤄 낼 수 있다.

하지만, timestamp embeddings 없이(wo/Pos.-Temp.) Autoformer의 성능은 빠르게 감소하는데 global temporal information의 손실 때문이다

대신에, temporal inductive bias를 introduce하기 위해 제안된 Frequency-enhanced module 덕분에 FEDformer는 position/timestamp embeddings를 제거하는 것으로부터 덜 영향을 받는다

Is training data size a limiting factor for existing LTSF-Transformers?

→ Training data size를 조절해보면서 성능 확인

몇몇은 Transformer base solution의 poor performance가 benchmark datasets의 작은 size때문이라고 논할지도 모르겠다.
Computer vision이나 NLP와는 다르게 TSF는 수집된 time series에 대해 수행된다, 그리고 이는 training data size를 크게 만들기 어렵게 만든다.
사실, training data의 size는 실제로 모델 성능에 큰 영향을 미치는 점은 인정한다
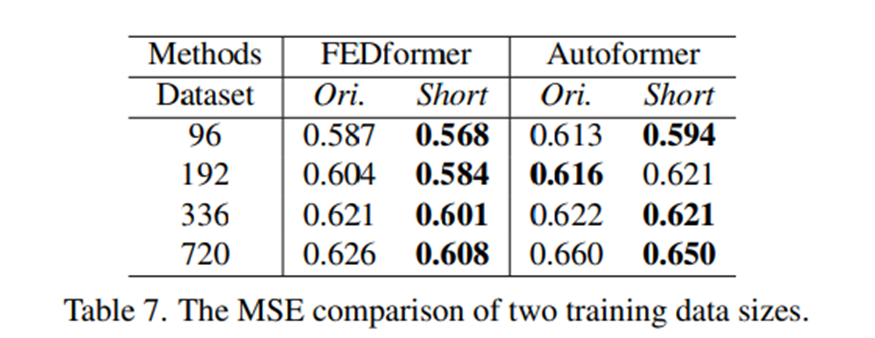
따라서 우리는 full dataset(17544*0.7 hours)[named Ori]에 대해 training한 모델의 성능을 그보다 좀 짧은 dataset(8760hours, i.e. 1years)[named Short]와 비교하면서 Traffic에대한 실험을 수행한다

뜻밖으로, Table7은 prediction error가 모든 forecast 케이스에 대해서 더 짧은 데이터가 더 낮음을 보인다.

몇몇은 Transformer base solution의 poor performance가 benchmark datasets의 작은 size때문이라고 논할지도 모르겠다.
Computer vision이나 NLP와는 다르게 TSF는 수집된 time series에 대해 수행된다, 그리고 이는 training data size를 크게 만들기 어렵게 만든다.
사실, training data의 size는 실제로 모델 성능에 큰 영향을 미치는 점은 인정한다
따라서 우리는 full dataset(17544*0.7 hours)[named Ori]에 대해 training한 모델의 성능을 그보다 좀 짧은 dataset(8760hours, i.e. 1years)[named Short]와 비교하면서 Traffic에대한 실험을 수행한다

뜻밖으로, Table7은 prediction error가 모든 forecast 케이스에 대해서 더 짧은 데이터가 더 낮음을 보인다.
이는 ori의 whole-year data가 더 길지만 short data가 더 Clear한 temporal features를 유지하고 있기 때문일 것이다.
우리는 training 할 때 무조건 더 작은 data를 사용해야 된다고 결론 내릴 수 없는 반면에 더 작은 data를 사용했지만 성능이 좋은 점은 training data scale이 Autoformer와 FEDformer의 성능에 대해 performance를 제한하는 이유가 아님을 보인다(-> clear한 temporal features가 중요하다)

Is efficiency really a top-level priority(정말로 효율성이 최우선 순위이냐)

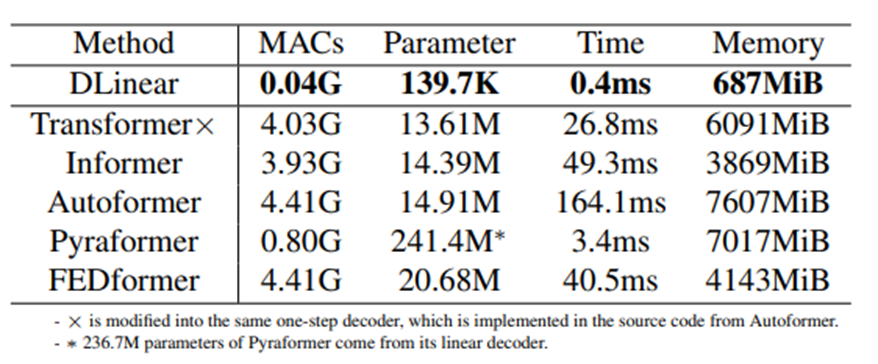
존재하는 LTSF-transformers는 Vanilla Transformer의 O(L^2 )의 복잡도는 LTSF problem에 대해 사용할 수 없다고 말한다
비록 그들이 이론적인 시간과 memory complexity를 O(L^2 )에서 O(L) 로 향상 시킬 수 있음을 증명했지만, 그들은 두가지 점에 대해서 불명확했다

1) the actual inference time and memory cost on devices are improved.
2) the memory issue is unacceptable and urgent for today’s GPU (e.g., an NVIDIA Titan XP here)
( memory issue가 과연 오늘날의 GPU에 대해 긴급한 issue인가)

Table8에서 우리는 average practical efficiencies를 비교한다.
흥미롭게도, Autoformer에 구현된 DMS decoder를 바꾼 vanilla transformer와 비교했는데, 대부분의 Transformer의 variants와 비슷하거나 심지어 더 나쁜 time과 parameters 추론을 초래했다.
이런 후속조치들(follow-ups)은 추가적인 design elements를 끼워 넣는데 이런 작업은 practical costs를 높게 만든다 더욱이 vanilla transformer의 memory cost는 output length L=720임에도 수용할 만하다, 이는 적어도 존재하는 datasets에 대해서 memory-efficient transformer 개발의 중요성을 약화시킨다

Future work

LTSF-Linear은 제한된 능력을 가진 모델이다 그리고 이 모델은 단순하면서도 경쟁력 있는 baseline이다
예를 들어 하나의 layer를 가진 linear network는 change points에 의해 발생하는 temporal dynamics를 capture하기 어렵다[25]
결과적으로, 우리는 새로운 모델 디자인들, data processing, 그리고 LTSF problem challenging을 가로막는 benchmarks에 대해 강한 potential 이 있다고 믿는다