Abstract

Multi-Horizon Forecasting은 보통 정적인 변수, 알고 있는 미래의 input, 다양한 Covariates, 과거에 대해서만 관찰된 exogenous Time Series까지 이와 같이 다양한 Input들이 복잡하게 섞인 형태의 input을 포함해서 Forecasting한다. 하지만 이때 이러한 Input들이 Target과 어떤 상호작용을 할지에 대해서는 사전정보가 없이 진행한다.
몇몇 Black-Box인 deep learning 모델들이 제안됐지만 이들은 모델에서 이런 다양한 Input들이 어떻게 사용되는지를 밝히지 않았다.
이 Paper에서 우리는 Temporal Fusion Transformer(TFT)를 소개한다
우리의 TFT는 novel(새로운) attention을 base로 한 architecture인데 Multi-horizon forecasting에서 뛰어난 성능 과 함께 temporal dynamics에 대한 Interpretable한 insights를 제공한다.

다양한 Scales에서 Temporal relationships를 배우기 위해서 TFT는 local processing을 위한Recurrent layers과 long-term dependency를 위한 Interpretable self-attention을 사용한다
TFT는 특별한 components(GRN)를 서로 관련 있는 Feature selection을 위해 활용하고 불필요한 component를 막기위해 gate layer(GLU)를 활용한다
이는 다양한 시나리오에 대해 high performance를 가능케 한다

Introduction

Multi-horizon Forecasting (i.e. the prediction of variables-of-interest at multiple future time steps) 은 중요한 문제이다.
One-step prediction과 대조적으로 multi-horizon forecast는 user에게 미래의 여러 step에 대해 그들이 어떤 action들을 취해야 할지를 알려주면서 전체 Path에 대한 추정을 제공한다.
Multi-horizon forecasting은 real-world application (retail, health care, economic)들에서 impactful하다.

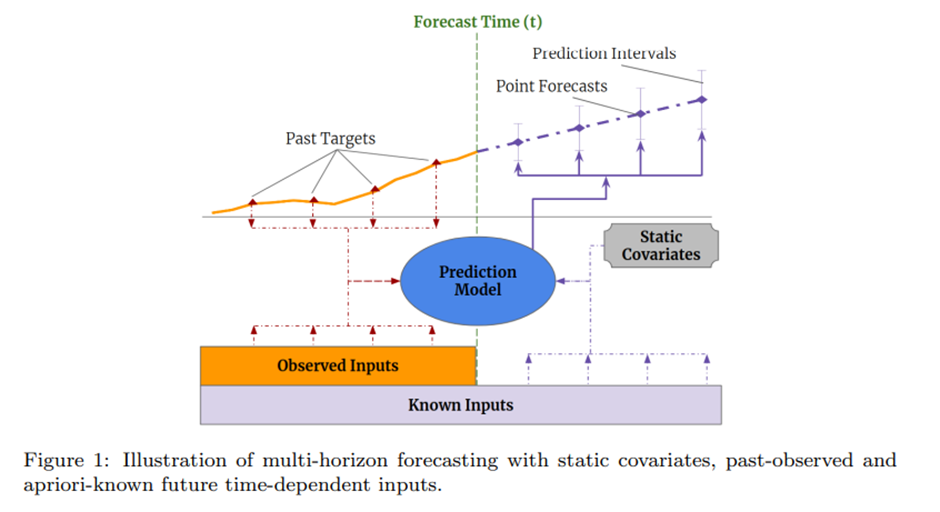
Practical Multi-horizon forecasting application은 fig1과 같이 미래에 대한 알려진 정보(e.g. 다가올 주말), 다른 exogenous time series(e.g. 역대 손님 방문한 횟수), static metadata(e.g. 상점의 위치)를 포함하는 다양한 data source에 접근한다-without any prior knowledge on how they interact
이렇게 그들이 서로 미치는 영향에 대한 적은 정보를 갖고 있는 data source의 이질성은 multi-horizon time series forecasting에서 challenging 하다.

Deep neural network는 traditional한 time series model보다 더 좋은 performance를 보여주면서 multi-horizon forecasting에 사용된다
많은 RNN base모델이 나왔는데 최근에는 과거에 관련이 깊은 time step들의 선택을 잘 하는 transformer 기반의 모델들이 많이 나왔다 하지만 이들은 multi-horizon forecasting에서 흔하게 보여지는 다양한 type의 input들을 고려하는 데에는 실패했다. 또한 이들은 모든 input 외생변수의 미래가 알려질 것이라고 가정하거나 혹은 중요한 static covariates를 다른 time-dependent feature에 붙여서 쓰는 등 경시한다.

우리는 suitable inductive biases들과 함께 네트워크를 디자인함으로써 multi-horizon forecasting에 대한 비슷한 성능을 얻어낼 수 있음을 보일 것이다
게다가 우리는 common multi horizon forecasting input의 이종성을 신경쓰지 않는다.
현재 대부분의 architecture가 forecast가 많은 파라미터 사이에 복잡한 비선형적인 관계에 의해 control되는 black-box model들이다
Model architecture가 black box일 때 이는 모델이 어떻게 예측과정에 도달하는지에 대한 설명을 어렵게 만들고 이는 user들이 모델의 output을 신뢰하는데 큰 어려움으로 작용한다
불행하게도, 흔하게 사용하는 DNN의 설명 method(LIME SHAP)들은 time-series에 적용하기에는 잘 맞지 않는다
이러한 post-hoc approach 들은 poor explanation quality를 이끌 것이다.
→Post-hoc method는 input feature들의 time ordering을 고려하지 않기 때문에
반면에 transformer와 같이 몇 가지 attention base architecture는 sequential data에 대한 내재된 해석가능성을 제안한다
하지만 Multi-horizon forecasting Task에 Transformer를 적용하는데 무리인 이유는 multi-horizon forecasting은 language나 speech와 반대로 다양한 type의 input feature를 포함한다.

Transformer는 관련이 있는 Time step에 대해서 insight를 제공할 수 있지만 그들은 특정 time step에 대해서 서로 다른 데이터 사이에 중요성을 구분할 수 없다.

따라서 우리는 multi-horizon forecasting에서의 높은 성능을 위해 데이터의 이종성(heterogeneity)을 해결할 새로운 method가 필요하다, 새로운 method들은 또한 forecast interpretable을 세우기 위해서라도 필요하다

SOTA보다 큰 성능 향상을 얻기 위해서, 우리는 여러 개의 주요한 idea들을 소개한다
(1) 네트워크의 다른 부분 들에서 사용하기 위한 context vector들을 encode하는 static covariate encoders
(2) 모델 전반에 걸친 Gating mechanisms 및 상관없는 input들의 기여를 최소화하기 위한 sample-dependent variable의 선택( variable selection에 자세한 설명 )
(3) 알려지고 관찰된 input들을 locally process하기 위한 seq2seq layer
(4) dataset안에 Long-term dependencies를 학습하기 위한 Temporal self-attention decoder

이런 특화된 component들의 사용은 interpretability를 가능케한다.
특히 우리는 TFT가 세가지의 가치 있는 interpretability의 사용을 가능케 함을 보여줄 것이다

HELPING USERS IDENTIFY
(1) prediction problem에 대해 전역적으로 중요한 variable
(2) 일관된 temporal patterns
(3) 중요한 events

Related Work

DNNs for Multi-horizon Forecasting

Traditional multi-horizon forecasting method와 비슷하게, 최근 deep learning method들은 autoregressive model을 사용한 iterated approaches 또는 seq2seq model을 베이스로 하는 direct method로 구분될 수 있다
Iterated approaches는 one-step ahead prediction model을 활용한다 multi-step predictions 은 재귀적으로 prediction을 future의 input으로 feeding함으로써 얻어진다 DeepAR, Deep State-Space Models(DSSM)등이 이러한 접근방식을 사용한다
그들의 Simplicity에도 불구하고 이런 iterative method 들은 Target을 제외한 모든 변수의 value들이 forecast time에서 알고 있어야 하는 가정에 의존한다 하지만 실제로는 time-varying input들이 많고 이들은 사전에 알려져 있지 않다
반대로, direct method들은 각각의 time step에서 미리 define한 multiple horizon에 대해 forecast를 생성하게 training된다
그들의 architecture들은 보통 seq2seq모델들에 의존한다 (e.g. 과거의 input들을 summary하기 위한 LSTM encoder와 future prediction들을 생성하기 위한 다양한 method를 사용, MQRNN)
LSTM base의 iterative method보다 더 좋은 수행을 보임에도 불구하고 interpretability는 direct methods들의 challenging으로 남아있다

Time Series Interpretability with Attention

최근에 Attention mechanism은 LSTM 과 Transformer 기반의 architecture를 사용하면서 interpretability motivation과 함께 Time series에 적용됐다.
하지만 이들은 static covariates의 importance에 대한 고려가 없었다.
TFT alleviates this by using separate encoder-decoder attention for static features at each time step on top of the self-attention to determine the contribution time-varying inputs.

Instance-wise Variable Importance with DNNs

Instance(i.e. sample)별로 다양한 importance가 post-hoc explanation method들과 Inherently-Interpretable modeling approaches에 의해 관찰될 수 있다
Post-hoc explanation method들은 pretrained black box 모델에 적용되고 자주 distilling into surrogate interpretable model 또는 decomposing into feature attribution에 기반한다
그들은 input의 time ordering을 고려(take into account)하도록 design 되지 않아서 복잡한 time series data에 사용하는 것은 제한된다
Inherently-Interpretable modeling approaches는 feature selection에 대한 구성요소를 직접적으로 모델 architecture안에 build한다.
Time series forecasting에 대해 Inherently-Interpretable modeling approaches은 time-dependent variable의 기여를 명시적으로 정량화 하는 것에 장점이 있다.

Temporal importance와 variable selection을 결합한 method들은 이미 고려됐었다. 이 method들은각각으로부터 계산된 attention weights(VSN 우측 확인)에 기반해서 single contribution coefficient를 계산한다

하지만, 한 스텝 앞 forecasts modeling의 Shortcoming에 더하여 existing method들은 또한 attention weight 들의 특정한 sample 에 대한 interpretation에 집중한다는 것이다(각각의 시점이 서로에게 얼마나 영향을 미치는지)- 이는 global temporal dynamics에 대한 insights를 제공하지 않는다

이와 대조돼서 sec7에서 TFT는 global temporal relationship들을 분석하는 게 가능하다는 것 과 그리고 TFT는 user들에게 전체 dataset에 대해서 모델의 global behaviors를 해석하는 것을 가능케 한다는 것을 보여준다– specifically in the identification of any persistent patterns(e.g. seasonality or lag effects) and regimes(제도) present

Review>
Abstract/Introduction/Related work에 대한 review
먼저 Multi-horizon forecasting에 대해서 현재까지 나온 모델들이 갖는 단점을 설명 한다 Multi-horizon forecasting에 관해서 현재까지 나온 Transformer기반의 모델들은 여러 데이터를 받아들이는 Multi-horizon forecasting에 대해 효과적이지 않고 Transformer 기반의 모델들은 오직 Temporal relationship에만 집중 돼있다 하지만 이 논문에서 제안하는 TFT는 특정 time step에서 여러 데이터들이 Target에 미치는 영향에 관한 insight를 제공하고 또한 기존의 Transformer 기반에 모델들과는 다르게 Interpretable self-attention과정에서 각각의 temporal relationship에만 집중하는 것이 아니라 우리 모델은 global temporal dynamics에 관한 insight를 제공할 수 있다 이러한 Interpretability로 기존의 black-model인 모델들과는 다르게 user들을 설득할 수 있고, 시계열에서 잘 맞지 않는 post-hoc method 대신해서 Target과 변수사이에 관계를 설명했다
이러한 Interpretability를 챙기면서도 SOTA성능을 달성한 것이 이 모델의 장점이다

Multi-horizon Forecasting

주어진 time series dataset에 I라는 고유한 객체가 있다고 하자 (e.g. health care 분야에 각 환자)
이러한 각 entity i 는 static covariate 집합 $s_i\in\mathbb{R}^{{m}_{s}}$와 inputs $X_{i,t}\in\R^{m_x}$ 와 scalar target인 ${y}_{i,t}\in\R$ (for $t\in\ {[0,T}_i]$) 관계돼 있다.

Time-dependent input features는 두개의 category로 나눠진다 ${X}_{i,t}=[z_{i,t}^T , x_{i,t}^T ]^T$
observed input $z_{i,t}^T\in\mathbb{R}^{m_z}$: 이는 각 step마다 측정되고 그 이후는 모르는 상태이고
known Input $x_{i,t}\in\mathbb{R}^{m_z}$∶ 이는 미리 결정된다

많은 경우에, prediction intervals를 제공하는 것은 decision을 최적화하고 risk를 관리하는데 있어서 유용할 수 있다( lower bound와 upper bound를 제공함에 있어서 )
우리는 lower bound와 upper bound를 구하기 위해서 quantile regression을 우리의 multi-horizon forecasting setting 에 적용한다 각각의 quantile forecast는 다음과 같은 형태를 갖는다

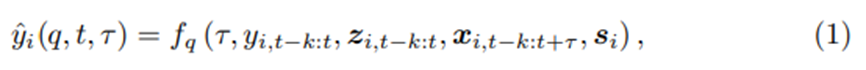
$\hat y_{i,t+τ} (q,t,τ)$는 t시점에서 ${\tau}$ step 앞 예측의 q- sample quantile이고 $f_q (.)$ 은 prediction model이다. 우리는 t로부터 k시점 이전 정보까지 사용한다

다른 direct methods와 마찬가지로 우리는 동시에 $τ_{max}$ time steps(i.e. τ∈{1,.., $τ_{max}$}에 대해 output forecasts를 낸다.
우리는 forecast start time t까지 target, known inputs(observed input, predetermined input)를 사용하면서 모든 과거정보를 포함한다
$y_{i,t-k:t}$=${y_{i,t-k},..,y_{i,t} } /z_{i,t-k:t}={z_{i,t-k},..,z_{i,t} }$ : target/ observed inputs until the t
$x_{i,t-k:t+τ}={x_{i,t-k},..,x_{i,t+τ} }$ : Known inputs across the entire range

Model Architecture

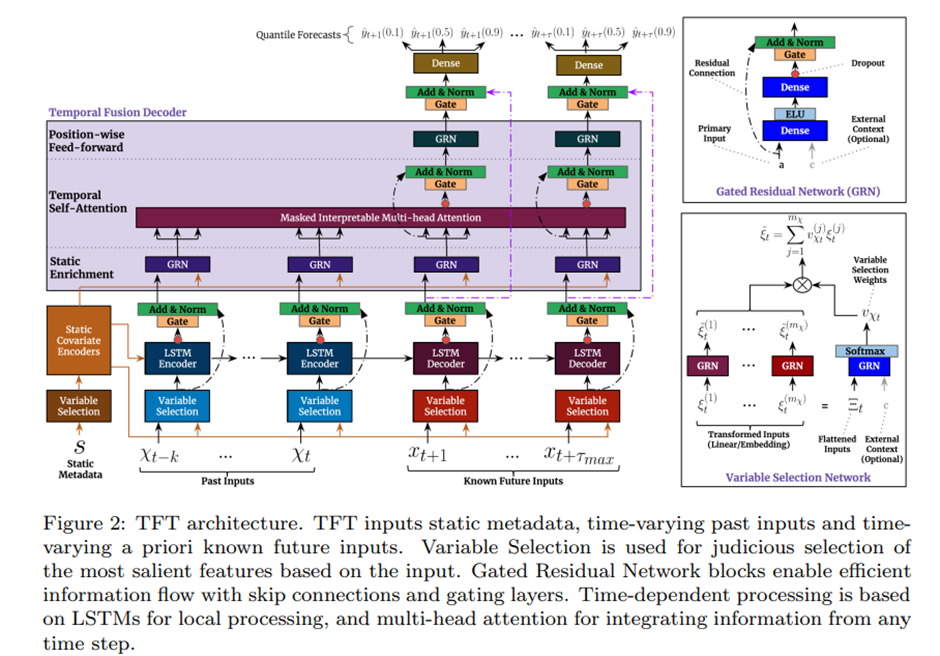
TFT의 메인 구성요소는 다음과 같다
1. Gating mechanisms: 이를 통해 architecture의 사용하지 않는 구성요소들을 Skip 한다
따라서 우리는 충분한 양의 데이터셋과 적절한 모델의 깊이 그리고 network에 복잡도를 챙길 수 있다
2. Variable selection networks: 매 time step마다 관련 있는 input variable을 선택한다
3. Static covariate encoders: static feature들을 context vector의 encoding을 통해 network에 합친다
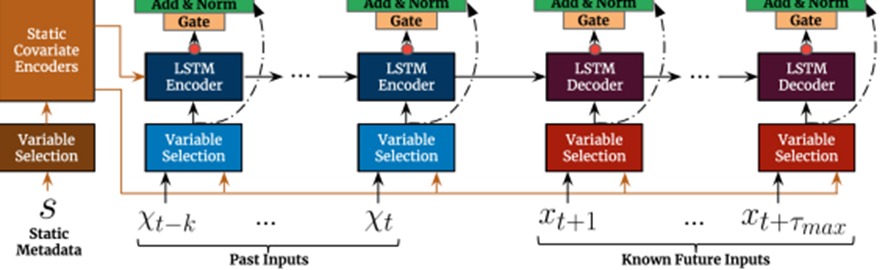
4. Temporal processing: Observed Input과 Known Input 모두에 대해 장기 단기 시간관계를 학습한다 Local Processing을 위해 seq2seq layer를 사용하고, Interpretable Multi-head attention을 통해 장기 의존성을 알아낸다
5. Prediction Intervals: 각각의 prediction horizon에서 target value의 범위를 결정할 수 있도록 하기 위해서 quantile forecasts를 사용한다

1. Gating Mechanism(GRN: Gated Residual Network)

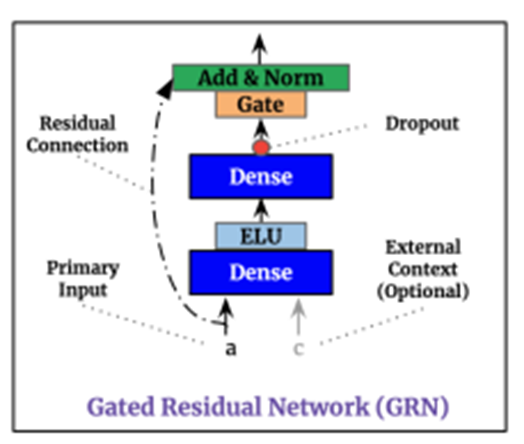
Exogenous inputs과 targets의 정확한 관계는 사전에 알려져 있지 않는다. 이는 어떤 variable들이 서로 관련이 있을지 예상하기 어렵게 만든다

비선형성의 정도를 부여해주는 GRN

또한 필요한 비선형 처리의 정도를 결정하기 힘들고 단순한 모델들이 훨씬 효과적일 수 있는 작거나 잡음이 심한 데이터셋이 존재하기도 한다.

이러한 motivation에 의해
모델에게 필요한 곳에만 non-linear processing을 적용하는 유연성을 주기 위해, 우리는 Gated Residual Network(GRN)을 제안한다

GRN은 초기input값인 a와 선택적 context vector c를 받고 다음을 생성한다

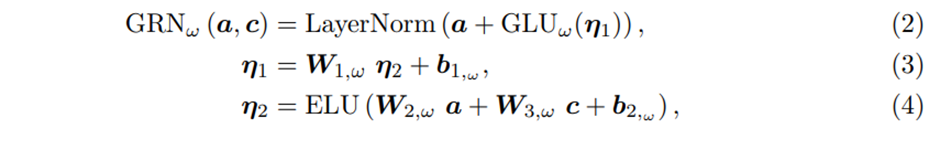
$η_1∈R^{d_{model}}$ $η_2∈R^{d_{model}}$ 는 모두 중간층에 해당하고 layer normalization을 사용했고 오메가는 weight sharing을 나타내는 index이다

$η_1$이후 외생변수들을 반영한 이 $\eta_1$을 얼마나 반영할지 GLU로 Gating 한다.
$η_2$는 input에 비선형성과 외생변수의 영향을 부과해주는 역할을 수행한다
$W_{2,ω} a + W_{3,ω} c+ b_{2,ω} >> 0$ 일 때 ELU는 identity function으로 행동하고
$W_{2,ω} a + W_{3,ω} c+ b_{2,ω} << 0$ 일 때 ELU는 (거의)constant output을 낸다

GLU(Gating Layer Unit)

우리는 GLU[모델 architecture의 gate를 의미]라는 gating layer를 architecture의 각부분에 사용함으로써 주어진 데이터셋[어떤 layer의 output]에 대해 architecture의 필요하지 않는 부분을 막는 유연성을 준다
GLU는 다음과 같다

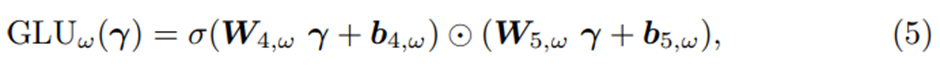
where
$W_{(.)}∈R^{d_{model} X d_{model}}$ , $b_{(.)} ∈R^{d_{model}}$ 는 각각 weight와 biases이다
⊙은 element-wise Hadamard product이다.
$γ∈R^{d_{model}}$ 인 Input
$\sigma$ = sigmoid function

GLU는 TFT에게 ‘GRN이 original input a에 기여하는 정도’를 control하게 허용한다[a에 비선형성을 추가할지 말지 control + a에 외생변수의 영향을 얼마나 반영할지 control] – 필요하다면 nonlinear contribution을 막기 위해서 GLU output이 거의 0에 가깝게 만들 수 있다 이로써 layer전체를 skip하는 효과를 낸다

전적으로 모델에게 모든 것을 맡기는 구조이다.

만약 context vector가 없다면 GRN은 context input을 0으로 취급한다

2. Temporal Variable Selection Networks

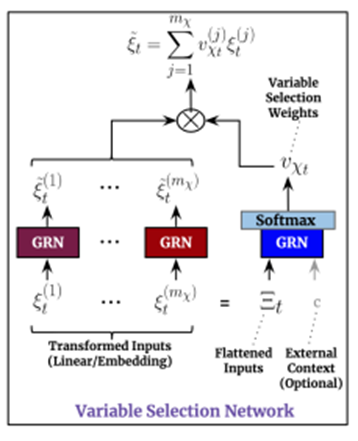
우리가 $m_χ$ 개의 data를 갖고 잇다고 가정하자 우리는 t시점에서의 variable selection을 통해 입력데이터를 encoding하고 싶은 상황이다. 각각의 data는 data의 종류에 따라 encoding 방식이 다를 것이고, 각각의 방식에 따라 이를 같은 크기의 벡터로 encoding을 시킨다 이를 여기선 $ξ_t^{(j)}$ 로 denote한다 이를 GRN에 통과시킴으로써 비선형성을 부과한 $\tilde ξ _t^{(j)}$로 만든다
총 $m_χ$개의 data의 t시점에 대해서 위와 같은 과정을 거친 후 이 각각의 data의 중요성을 판단하는 과정을 데이터를 Flatten시킨 $Ξ_t$ 와 static한 데이터의 context vector인 $c_s$를 GRN에 통과시킴으로써 비선형성을 부과하고 이때 output에 영향을 크게 미치는 data에 대해 높은 가중치를 주기를 기대한다 이후 Softmax를 통과시켜서 variable selection weights 인 일종의 score를 부과하고 이를 각각 곱하고 summation시켜서 최종적인 input을 만들어낸다

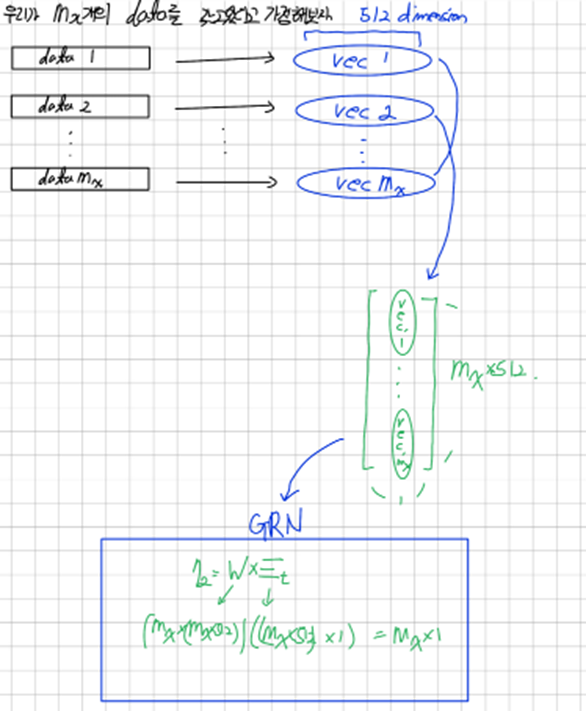
다양한 variables[Time series data]가 사용가능한 반면, 그들의 relevance와 구체적인 output에 대한 기여는 보통 알려져 있지 않다.

TFT는 static covariates와 time-dependent covariates를 둘 다 적용한 variable selection networks를 사용함으로써 instance(sample)[=각각의 time-step] 별로 variable selection을 제공한다
어떤 variable이 prediction problem에서 가장 중요한지 insights를 제공해주는 것[variable selection weight를 통해] 뿐만 아니라, variable selection은 TFT에게 예측 성능에 악영향을 미치는 불필요한 noisy input들을 제거할 수 있게 한다

대부분의 실제 시계열 데이터셋에는 예측과 관련 없는 값들이 많으므로, 변수 선택은 모델의 성능향상에 큰 도움이 된다

Categorical Variables에 대해서는 Entity Embedding을, Continuous Variables에 대해서는 Linear Transformation을 진행한다 – 이는 subsequent layer에 각각의 input variable을 d_model-dimensional 벡터로 변환하는 것이다

Repeat
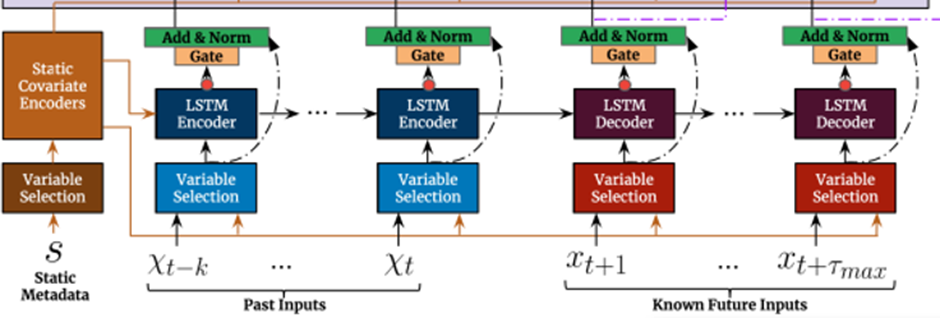
모든 Static, past and future input들은 서로 다른 variable selection networks를 사용하고 이는 fig2에서 다른 색깔로 구분돼 있다
$ξ_t^{(j)}∈R^{d_{model}}$ 를 시점 t에서 j번째 variable의 변환된 input이라고 denote 하자 {pronounce xi}
$Ξ_t=[ ξ_t^{(1)^T} ),.. ,ξ_t^{(m_x )^T } ]^T$ 는 시점 t에서 모든 input들의 Flatten된 vector이다.
Variable selection weights는 $Ξ_t$ 그리고 external context vector $c_s$를 GRN과 Softmax layer에 feeding을 함으로써 생성된다

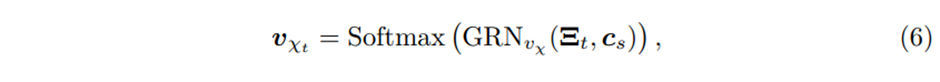
Where
$v_{χ_t}∈R^{m_χ}$ 는 variable selection weights의 vector이다
Static한 데이터의 context vector $c_s$ 는 static covariate 인코더에서 얻어진다
우리는 각 시점에서 비 선형적인 processing을 GRN에 $ξ_t^{(j)}$를 feeding 함으로써 구한다

Note
모든 variable은 모든 시점 t에 대해 가중치를 공유하는 그들 자신만의
$GRN_{ξ(j)}$ 을 갖는다[오메가의 역할: 이렇게 한 데이터셋에 대해 시점과 상관없이 같은 가중치를 같게 함으로써 시간이 지남에 따라 어떤 데이터가 Target에 미치는 전체적인 영향력을 반영 가능하다 (내의견)] 이러한 Processed feature는 그들의 variable selection weights를 곱하고 더한다

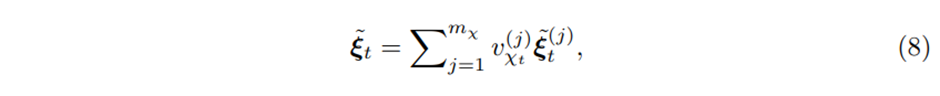
3. Static Covariate Encoders

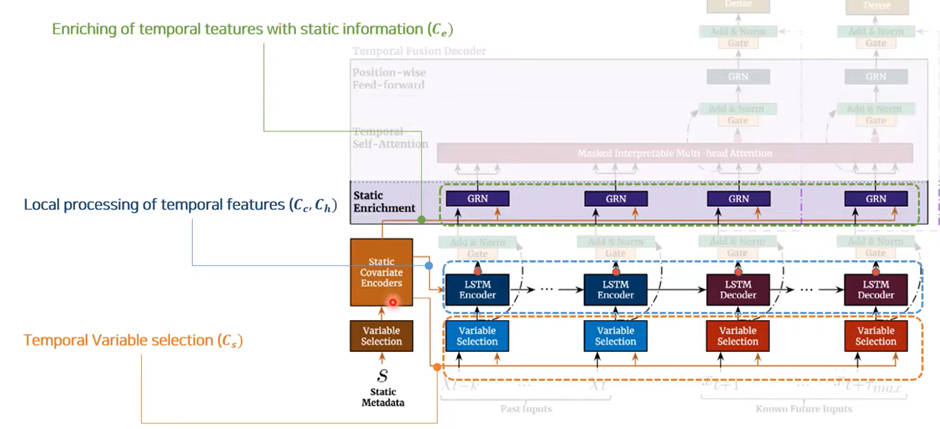
다른 time series forecasting architecture들과 달리, TFT는 정적인 메타데이터(데이터를 위한 데이터)로부터 정보를 합치기 위해 신중하게 디자인됐다
네 가지의 서로 다른 different context vectors, $c_s,c_e, c_c,c_h$를 만들기 위해서 서로 다른 GRN encoders를 사용한다

1. Variable selection에 사용하는 context vector인 $c_s$

2. local processing of temporal features에 사용하는 $c_c,c_h$ context vectors

3. Enriching of temporal features with static information에 사용하는 $c_e$ context vector 가 있다

예로써, $ζ$를 static variable selection network의 output이라 하자, temporal variable selection에 대한 contexts는 다음과 같이 encoding 된다

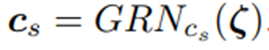
4. Interpretable Multi-head Attention

TFT는 long-term dependency를 잘 capture하기 위해서 self-attention을 도입했다
우리는 attention의 explainability를 강화하기 위해서 transformer에서 사용하는 multi-head attention으로부터 약간 수정을 거쳤다
General한 self-attention>

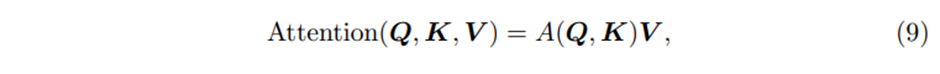
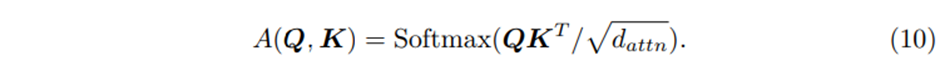
Standard attention mechanism의 learning하는 능력을 향상시키기 위해서 multi-head attention mechanism을 적용시켰다

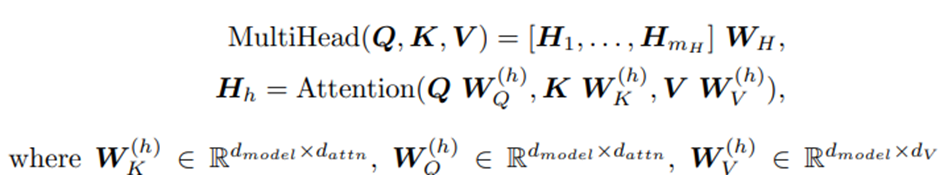
각 head에서 다른 value들이 사용된다는 점을 고려하면, attention weight는 단독으로 특정 feature의 중요성을 나타낼 수 없다. 이러한 점 때문에 우리는 multi-head attention을 value를 공유하는 방향으로 수정하고 모든 head에 대해서 additive aggregation을 적용하고 평균을 취해주는 과정을 거친다

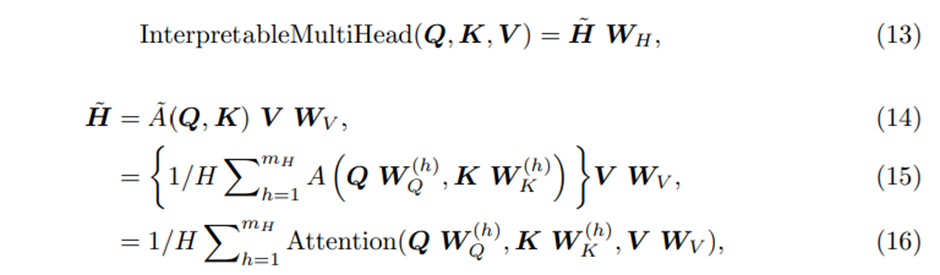
Where
$W_V∈R^{d_{model} X d_V}$는 모든 head에 걸쳐 공유되는 value weights이다
$W_H∈R^{d_{attn} X d_{model}}$ 은 final linear mapping으로 사용된다

우리는 이를 Combined matrix $\tilde A(Q,K)$ 로의 attention weights에 대한 simple ensemble로 해석할 수 있다
A(Q,K) 와 비교했을 때 우리는 Value 별로 Attention score에 대해 효과적으로 설명할 수 있다 따라서 효과적인 방식으로 representation capacity를 향상시켰다고 할 수 있다

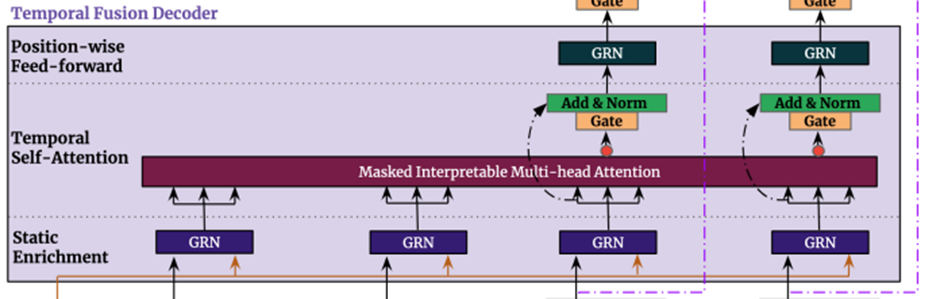
5. Temporal Fusion Decoder

Temporal fusion decoder는 dataset에서 보여지는 temporal relationship을 배우기 위해서 아래와 같은 layers를 거친다

5.1 Locality Enhancement with sequence-to-sequence layer(seq2seq layer로 지역성 강화)

Locality: 입력에서 각 sample간의 관계가 서로 가까운 요소들에 존재한다는 의미이다
Translation Invariance: 입력과 동일하게 계속해서 관계가 유지된다는 것을 말한다.

시계열 데이터에서 주변 value들 사이의 관계는 매우 중요한데
따라서 attention-based architecture에서 Local context를 활용하는 것은 Performance 향상을 이끌 수 있다.(informer에서 1-D convolutional network)

---

[12] S. Li, et al., Enhancing the locality and breaking the memory bottleneck of transformer on time series forecasting, in: NeurIPS, 2019.

---

예를 들어, [12]에서는 지역성 강화를 위해 single convolutional layer를 채택한다 – extracting local patterns using the same filter across all time.

하지만, 이는 observed input들이 존재할 때 과거의 input 변수의 개수와 미래의 input변수의 개수가 다르기 때문에 적절하지 않을 수 있다.

나의 해석
하나의 합성곱 신경망으로 Locality를 강화 시킬때, 미래에 입력받는 입력은 입력이 과거와 다르게 될 수 있는데, 이때의 입력값에 과거부터 사용한 합성곱 신경망의 가중치를 사용하는 것은 적절하지 않을 수 있다.

이러한 점 때문에 우리는 이런 개수의 차이를 자연스럽게 handle할 수 있는 seq2seq모델의 적용을 제안한다 - $\tilde ξ_{t-k:t}$ 가 encoder에 feeding되고 $\tilde ξ_{t+1:t+τ_{max}}$ 가 decoder에 feeding 된다.
그러면 이는 uniform 한 temporal feature들의 집합을 생성한다 이는 temporal fusion decoder에 input으로써 serving된다
Denote (pronounce pi)
$ϕ(t,n) ∈ { ϕ(t,-k),.. ,ϕ(t,τ_max ) }$
n is position index.

이런 LSTM cell series를 적용하는 것은 Inputs의 시간 순서에 대해 적절한 inductive bias 를 주면서 (Sequential & Temporal Invariance의 Relational Inductive Biases를 갖는다. Sequential이란 입력이 시계열의 특징을 갖는다고 가정하며, Temporal Invariance는 동일한 순서로 입력이 들어오면 출력 순서도 동일하다는 것을 말한다.)

Inductive Bias는 보지 못한 데이터에 대해서도 귀납적 추론이 가능하도록 하는 알고리즘이 가지고 있는 특징.

Ex> CNN의 Locality& Translation Invariance
여기서, Localitiy는 입력에서 각 Entities간의 관계가 서로 가까운 요소들에 존재한다는 것을 의미한다. 그리고 Translation Invariance란 입력과 동일하게 계속해서 관계가 유지된다는 것을 말한다. 이는 무엇을 의미할까? 어떤 특징을 가지는 요소들이 서로 모여있는지가 중요한 문제에서 좋은 성능을 보여준다는 것을 의미한다. 이러한 이유에서 CNN이 이미지 관련 문제에서 강점을 보이는 것이다.

Ex> RNN의 Sequential & Temporal Invariance
RNN은 시간의 개념을 사용하는 것이다. RNN에서는 CNN의 Locality & Translation Invariance와 유사한 개념으로 Sequential & Temporal Invariance의 Relational Inductive Biases를 갖는다. Sequential이란 입력이 시계열의 특징을 갖는다고 가정하며, Temporal Invariance는 동일한 순서로 입력이 들어오면 출력도 동일하다는 것을 말한다.
이러한 가정들의 장점은 가정이 맞는 경우 좋은 성능을 보여준다는 것이다. 하지만, 가정이 맞지 않는 경우에는 매우 약한 모습을 보여준다.
출처

더욱이 local processing에 영향을 미치는 static metadata를 고려하기 위해서 $c_c,c_h$ context vector를 각각 cell state와 hidden state의 초기값으로 사용한다
또한 우리는 gated skip connection을 이 layer위에 적용한다

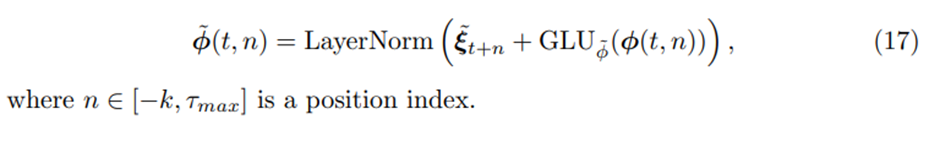
Gate를 통해서 영향을 받지 않은 값에 Gating 하여 흘려보내준다.(Likely, Residual Connection)

5.2 Static Enrichment Layer

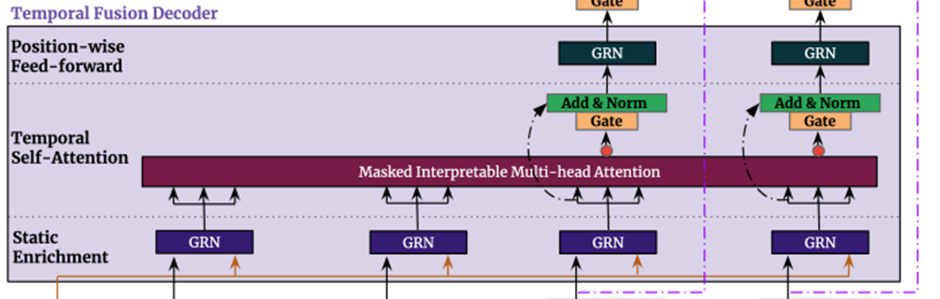
Static covariates는 자주 큰 영향력을 갖고 있어서 temporal dynamics에 큰 영향을 미친다 [e.g. 시간에 따른 disease risk에서 특정 유전자의 영향]
우리는 static metadata와 함께 temporal feature를 강화하는 static enrichment layer를 소개한다
주어진 position index n에 대해 static enrichment는 다음과 같은 형태를 갖는다

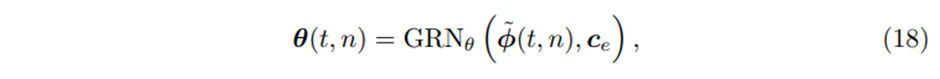
이때 $GRN_θ$의 가중치는 전체 layer에 걸쳐 공유되고, $c_e$는 static covariate encoder로부터 구해진context vector이다

5.3. Temporal Self-Attention Layer

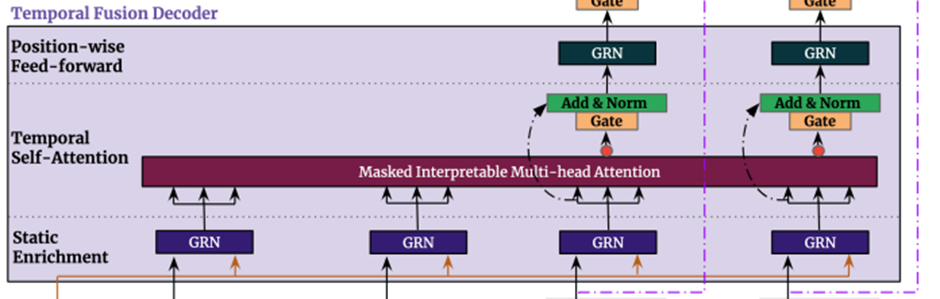
Static enrichment이후에 우리는 self-attention을 적용한다
먼저 모든 Static-enrichment output을 하나의 single matrix로 Group화 한다 – $i.e. Θ(t) = [θ(t,-k),..,θ(t,τ)]^T$
그리고 interpretable multi-head attention을 각각의 forecast time에 적용한다(With $N=τ_{max}+k+1$)

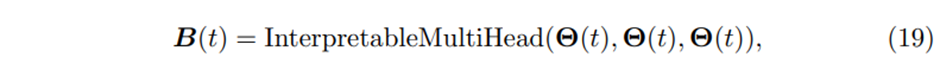
$B(t) = [β(t,-k),..,β(t,τ_max )]^T$ 이다
$d_V = d_{attn}=d_{model}/m_H$ 는 선택되며, $m_H$ 는 head의 개수이다

Decoder masking은 각각의 temporal dimension 이전의 feature들에 대해서만 참여할 수 있는 것을 보장하기위해 적용한다
게다가 masking을 통해 causal information을 유지하면서, TFT가 RNN base architecture가 학습하기 어려운 long range dependency를 학습할 수 있게 만들어줬다.

위 그림은 실제로 forecast를 하는 것에 대한 그림이다 따라서 아래의 GLU를 forecast time에만 적용을 했고 이를 통해 생각해 볼 수 있는 것은 training과정에서는 Masked Interpretable Multi-head Attention을 적용해서 나오는 output을 $t+τ_{max}$까지 만들어서 가중치를 training시키고 실제로 forecast할 때는 나오는 output을 $τ_{max}$ 개만큼만 사용하여 forecasting 한다

Self-attention layer다음으로 추가적인 gating layer를 적용함으로써 training이 가능하게 했다

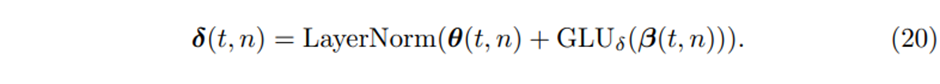
5.4. Position-wise Feed-forward Layer

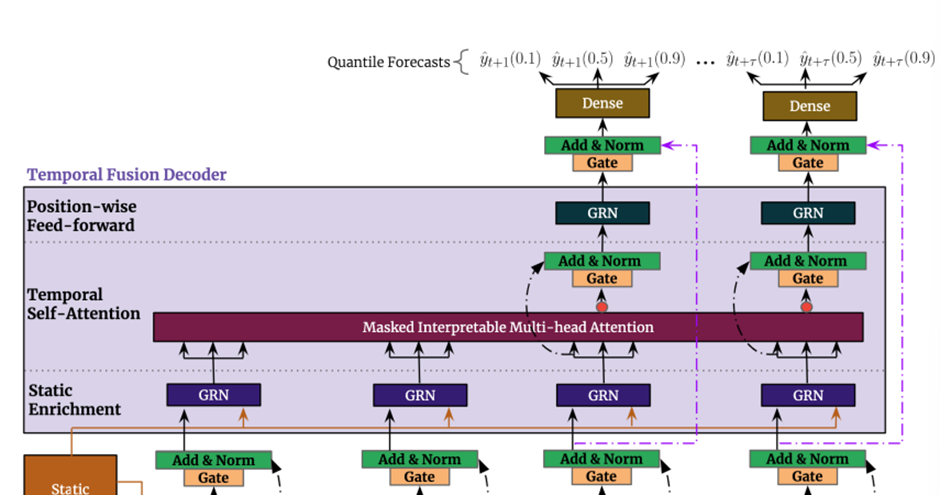
우리는 self-attention layer의 outputs에 추가적인 non-linear processing을 적용한다
Static enrichment layer와 비슷하게, 이는 GRN의 사용으로 만들어진다:

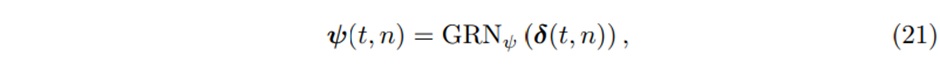
$GRN_ψ$의 가중치는 전체 layer에 걸쳐서 공유된다. 또한 우리는 gated residual connection을 적용하는데 이는 전체 transformer block을 건너 뛰어서 연결된다.

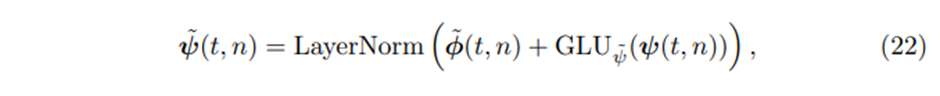
이렇게 residual connection을 함으로써 decoder를 거친 값을 얼마나 반영할지 정해준다.

→ Temporal fusion decoder를 거치지 않을 경우는 그냥 time-series의 seq2seq 모델임

5.5.Quantile Outputs

TFT는 Prediction Intervals를 생성한다.
이는 매 time step에서 다양한 percentiles(10,50,90)에 대한 동시 예측을 통해서 얻어진다
Quantile forecasts는 temporal fusion decoder의 output으로부터 linear transformation을 사용해서 생성된다

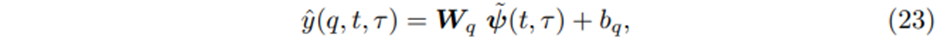
Where
W_q∈R^(1 X d), b_q∈R 는 특정한 quantile q에 대한 계수들
Note
Forecasts are only generated for horizons in the future – i.e. 〖τ∈{1,..,τ〗_max}

Loss function

TFT는 jointly minimizing the quantile loss에 의해 training된다


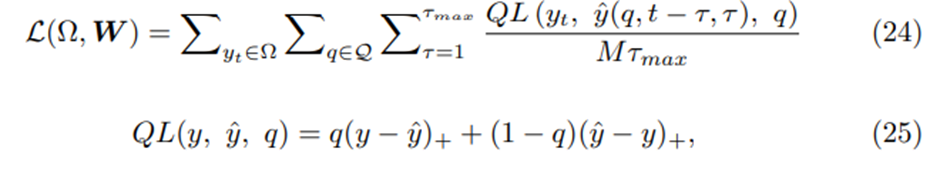
$t-\tau$까지는 예측하고자하는 target의 정보를 사용한다.

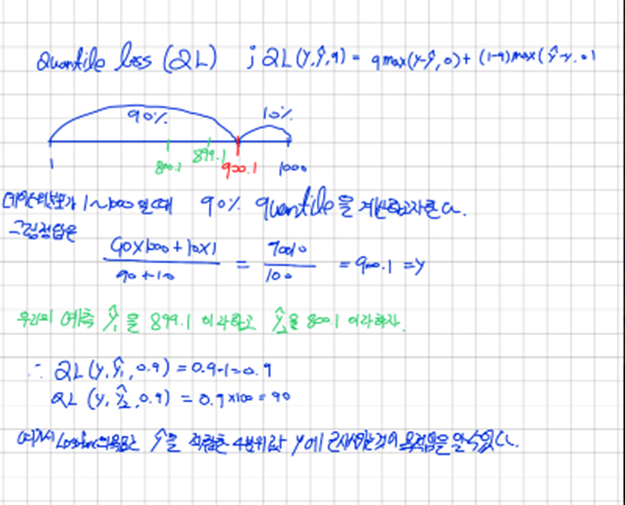
$L(Ω,W)$의 목적은 t시점과 우리가 정한 quantile 들의 집합인 Q의 각 quantile에 따라 t시점을 예측하는데 tau에 따라 다음을 $\hat y(q,t-τ,τ)$ 예측하고 이들의 quantile loss를 구하고 평균을 한 후 $y_t$의 데이터셋을 바꿔가면서 summation후에 평균을 한다
우리는 q-Risk를 사용하는데 이는 entire forecasting horizon에 걸쳐 normalized한 quantile loss식이다(weighted quantile loss)

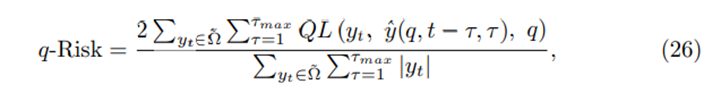
Interpretability use cases

우리 모델의 Performance benefits를 확립한 이후, we next demonstrate how our model design allows for analysis of its individual components to interpret the general relationships it has learned 우리는 3가지의 interpretability use cases를 보여줄 것이다
(1) 예측에 들어가는 input variable 각각의 중요성을 examining
(2) Persistent temporal patterns를 visualizing
(3) Temporal dynamics안에 중대한 변화를 이끄는 any regimes(제도) 또는 사건들을 identifying

Analyzing Variable Importance

우리는 먼저 variable selection weights를 분석함으로써 variable importance를 알 수 있다.
구체적으로, 전체 test set에 걸쳐 각각의 variable에 대해 selection weights를 모으고 이렇게 모은 variable selection weights의 percentile들을 기록한다
Retail dataset은 이용가능한 input types(i.e. static metadata, known inputs, observed inputs and the target)를 모두 포함하고 있기 때문에, 우리는 Table3에서 그것들의 variable importance analysis에 대한 결과를 Table3에서 보인다

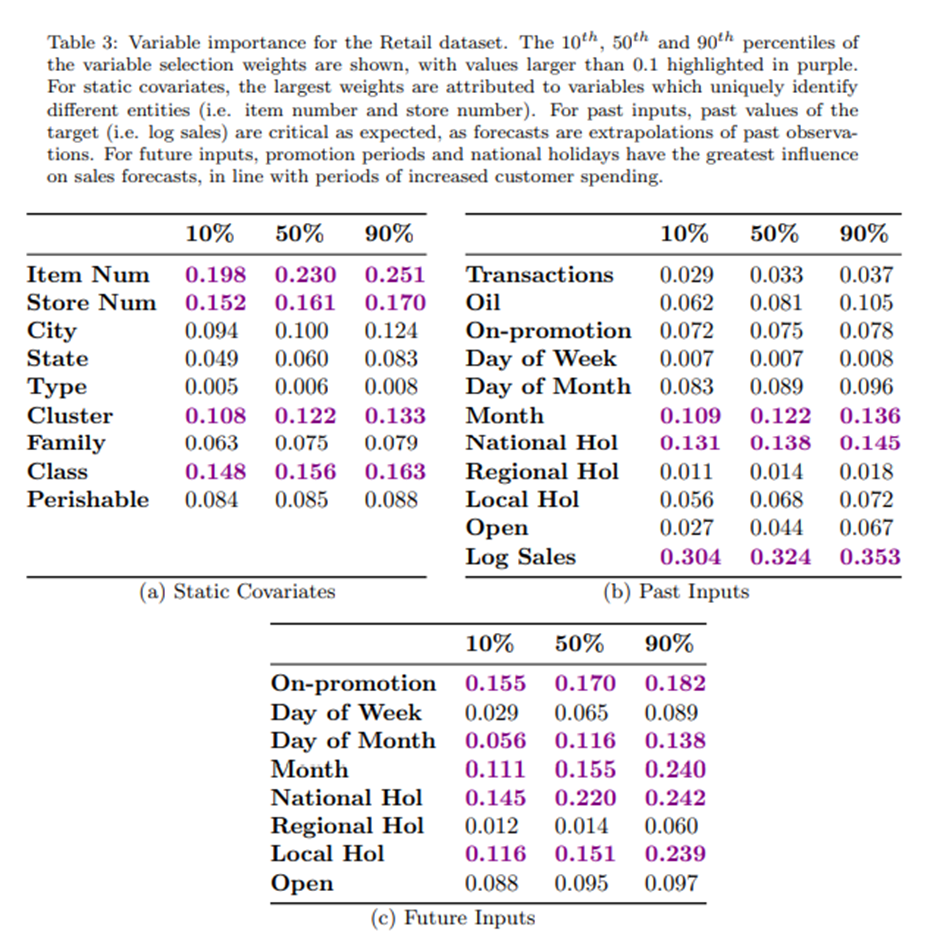
• Static covariates에 대해서는 variable 독특하게 다른 객체들을 확인하는 variable이 large weight를 갖는다(Item Num, Store Num)
• Past inputs에 대해서는 target의 과거 values가 예상대로 critical 했다
• Future inputs에 대해서는 promotion periods와 national holidays가 가장 큰 영향력을 지녔다

Table3에서 결과는 TFT가 직관적으로 예측에서 중요한 역할을 하는 key inputs를 추출하는 것을 보인다

persistent temporal patterns

persistent temporal patterns의 분석은 주어진 데이터에 나타나는 time-dependent relationships를 이해하기위해서 자주 핵심이 된다
예를 들어 lag models는 영향이 있기까지 필요한 시간을 연구하기 위해 자주 채택된다

• Such as 정부의 공공지출 증가가 국민총생산(Gross National Product)의 중가에 미치는 영향

Seasonality models 또한 흔히 경제 분야에서 흥미 있는 target의 주기성 패턴과 cycle의 길이를 알아보기 위해서 사용된다

→ 이전까지 Persistent temporal pattern을 알아보기 위한 방법들

실용적인 견해로부터, 모델 설계자들은 forecasting model의 성능을 더욱 향상시키기 위해서 아래와 같은 insights를 사용할 수 있다
– 예를 들어 만약 attention peaks가 lookback window의 시작에서 관찰 된다면 더 많은 history를 포함하기 위해서 lookback window(=receptive field[ in paper ])를 증가시키거나 seasonal effects를 직접적으로 포함하기 위해서 feature engineering을 할 수 있다

이와 같이, temporal fusion decoder의 self-attention layer에 존재하는 attention weights를 사용하여 우리는 similar persistent patterns를 확인하는 method를 제시한다
-> interpretability self-attention

Eq.14와 19을 결합하여, 우리는 self-attention layer가 각각의 forecast time t에서 attention weights의 행렬을 포함하는 것을 본다 – i.e. $\tilde A(ϕ(t),ϕ(t)).$

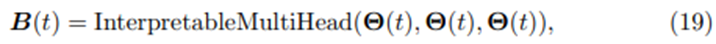
각 forecast horizon $τ$ 에서 Multi-head attention outputs(i.e. $β(t, τ)$)는 각각의 position n에서 더 낮은 level의 feature들의 attention-weighted sum으로 표현할 수 있다

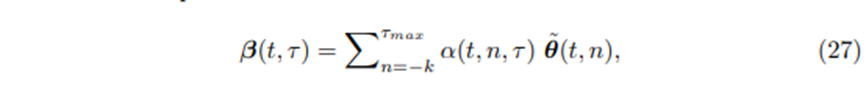
Where $α(t,n,τ)$ 는 $\tilde A(ϕ(t),ϕ(t))$ 의 $(τ,n)$번째의 element[즉, n번째 key와 $\tau$번째 query사이의 유사도 score] 그리고 $\tildeθ(t,n)$은 $\tilde Θ(t)= Θ(t) W_V$의 n번째 row이다

→ 결론:
1. TFT의 Variable selection이 직관적으로 예측에서 중요한 역할을 하는 feature들을 뽑아낼 수 있다
2. TFT의 interpretability self-attention이 예측에 미치는 기여도를 측정함으로써 similar persistent pattern을 확인 할 수 있다