Feature Importance

우선, feature importance에 관해서 알아보자.
먼저 트리 기반 모델들(random forest, xgboost, lightgbm 등)은 기본적으로 feature importance를 API 혹은 모델 내장 함수로 제공한다.
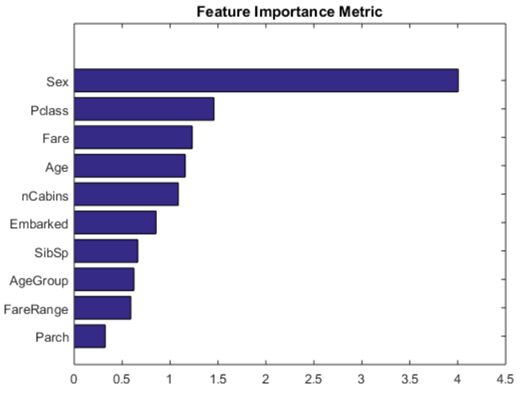위 그림은 Kaggle의 타이타닉 생존자 예측에서 사용된 Feature Importance 그림이다. 그런데 이렇게 구해진 Feature Importance가 과연 정확할까? 즉, 실제로도 성별이 가장 영향을 많이 미칠까? 실제로는 그렇지 않다. 이를 알기 위해서는, Feature Importance를 구하는 방식을 먼저 알아보겠다.

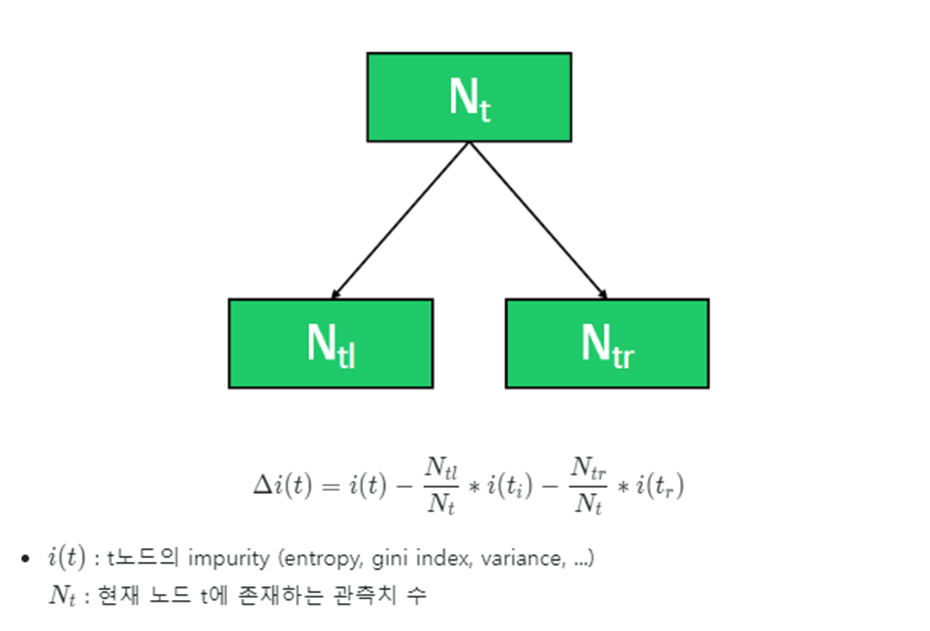
트리기반 머신러닝 모델에서는 각 Feature별로 엔트로피(Entrophy)[불확실성] 혹은 지니 계수라 불리는 것들을 계산해서 가지치기를 한다. (fit과정)
엔트로피와 지니계수 자체는 이 노드가 얼마나 불균일한가를 측정하고 이를 통해서 얼마나 균일하게 만드는지를 측정하여서 Feature Importance로 사용한다.

---

<엔트로피 & 크로스엔트로피 참고>

MyVelog

엔트로피
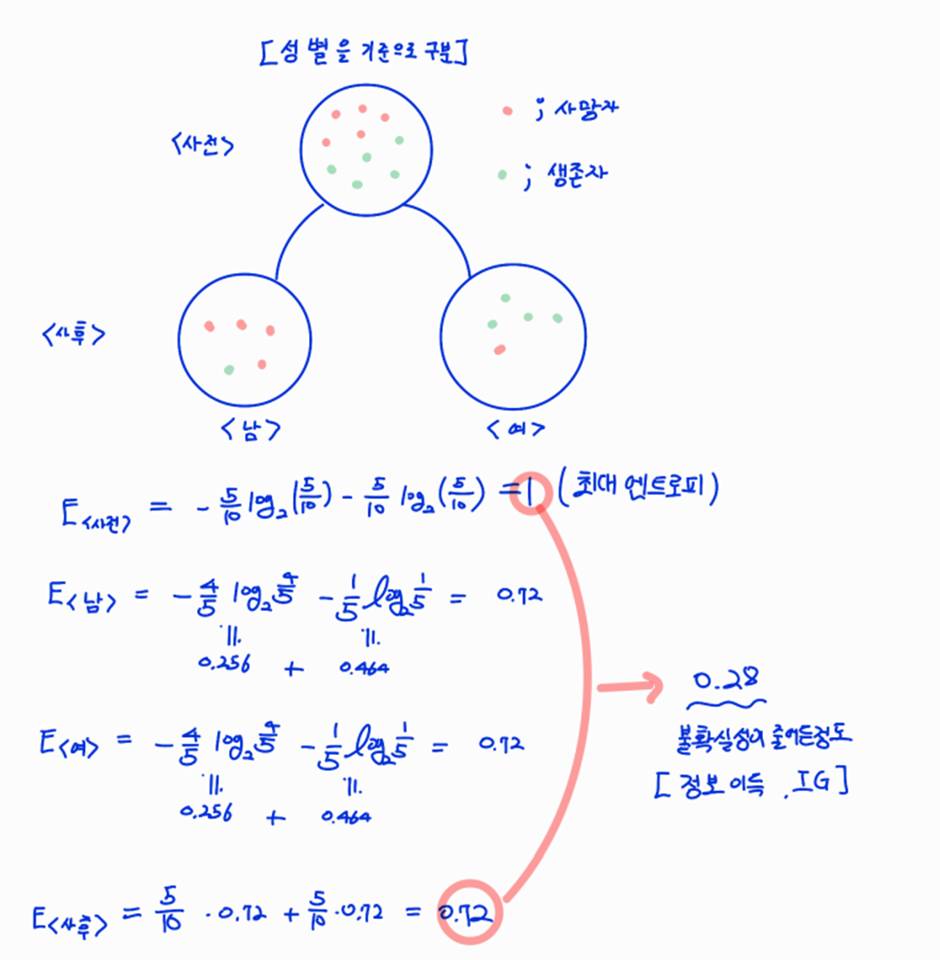
먼저, 직관적인 이해를 위해 물리공부를 했을때를 떠올려보면 엔트로피라는 말은 불확실성과 동치인 말이었다. 이를 그대로 생각해보면, Tree에서 분류하는 과정에 있어서 적절한 Feature를 사용해서 분류를 하는 경우에는 잘 분류가 될 것이고, 이는 곧 불확실성이 낮게 나오게 된다.
그렇다면 얼마나 불확실성이 낮아졌을까? 라는 말은 -> 정보를 얼마나 얻어서 불확실성이 낮아졌을까? 로 대치가 되고, 이것이 의미하는 것이 바로 정보이득(Information Gain)[IG]이다.

지니계수(Gini Index)
지니계수는 얼마나 Impure한지를 측정하는 지표이다. 따라서 지니지수가 0 이라면, 이는 해당 클래스가 모두 ‘같은 Class’ 이기 때문에, 아주 Pure한 상태를 말하는 것이고 가장 Impure한 상태는 당연히 절반 절반 클래스가 섞여있을때이고 이때의 지니계수는 1/2 이다.
Gini Index는 다음과 같이 계산한다. Gini Split은 분기하는 기준을 정하기 위해서 사용하는 지표이다. [자식 노드의 Gini Index를 weighted sum을 취한다.]

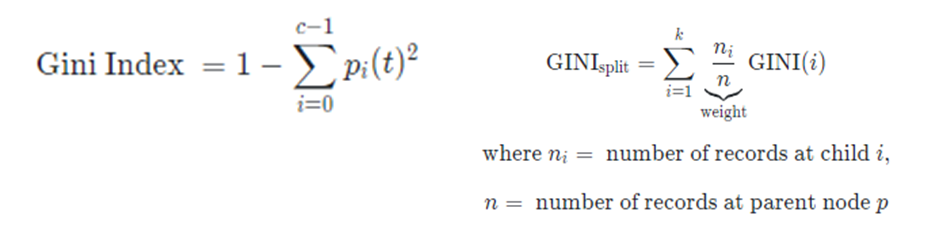
C 는 클래스의 총 개수

아래의 예시를 확인해보자

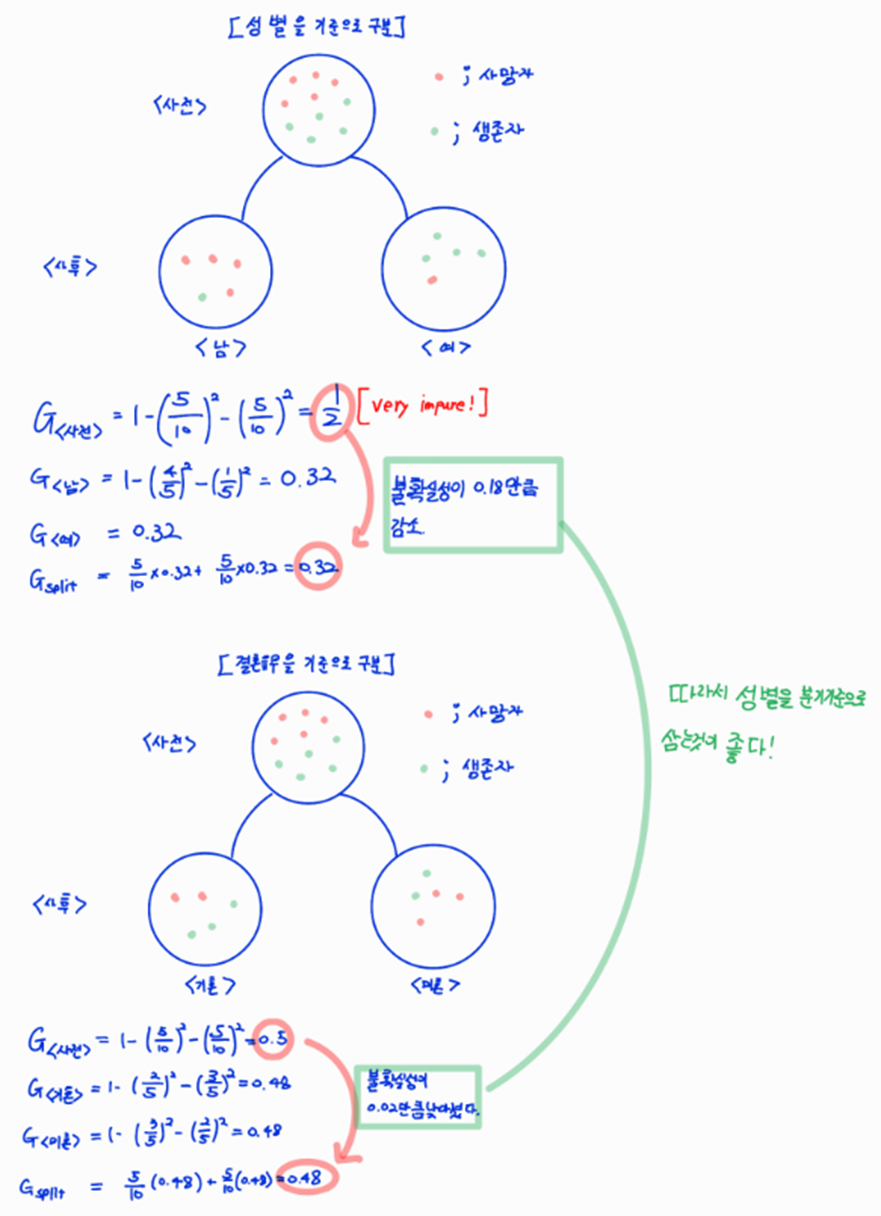
정보이득 그리고 Gini Split을 이용해서 트리를 분기함을 알 수 있다.

참고1
참고2
참고3

---

우리는 위와 같이 불확실성을 낮추는 방향으로 노드를 이어나간다. 이때 위에서 구한 다양한 측도(measure)를 이용해서 우리의 Feature Importance를 구하는 방법은 MDI와 같은 것들이 있다.

MDI(Mean Decrease Impurity)

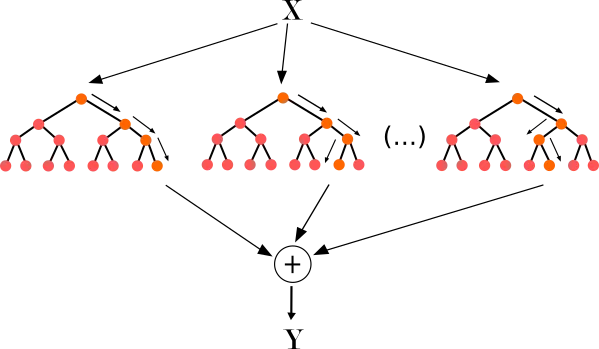
MDI(Mean Decrease Impurity)는 감소분[Information Gain, Gini_split]의 평균을 중요도로 정의하는 것이다.
아래의 그림처럼 차이를 구한이후 앙상블의 전체 tree에서 해당 Feature를 포함하는 수 만큼 다 더한이후, 그것을 평균낸다

MDI의 장점: 빠르고 직관적
MDI의 단점: 여러종류(high cardinality)를 갖는 범주형 Feature는 트리가 분기될 때 이용될 확률이 높다.(why? /Self answer-> 여러종류 범주이면 정보이득이나 gini 계수의 차를 계산하는 과정에서 빠지는 것이 많기 때문에 좀더 변화의 크기가 커져서 이용될 확률이 높다) 그래서 전체적인 일반화보단 범주가 많은 Feature에 대해서 과적합을 일으키기 쉽고, 따라서 Pure하게 구분될 확률이 높아 빠지는 값이 적어 Δi(t) 값이 높게 나온다.(<-> Feature Importance가 높게 나올수 있다) 따라서 이 경우 잘못된 해석이 되지 않도록 조심하여야 한다.

참고
참고2

Permutation Importance

Permutation Importance는 이전에 SHAP/LIME에 비해서 개념이 쉽다. 또한, LIME과 SHAP과 달리 모델의 Feature에 대한 전역설명을 위해서 검증 데이터의 특정값을 무작위로 섞어서 중요도를 계산한다.

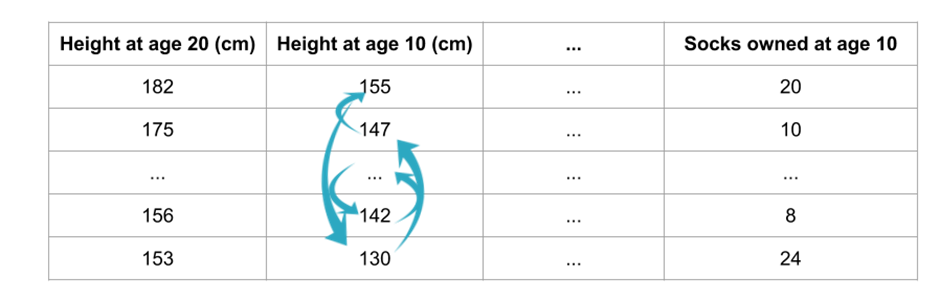
위와 같이 Feature의 값을 무작위로 섞는다. 이렇게 뿔뿔이 흩어진 Feature 값은 모델에서 Noise처럼 도움이 되지 않는다. 만약 위에서 처럼 섞었는데 예측 오차가 증가할경우, 예측은 이 Feature에 의존함을 알 수 있다. 꽤나 직관적인 설명이다.

https://www.kaggle.com/code/dansbecker/permutation-importance

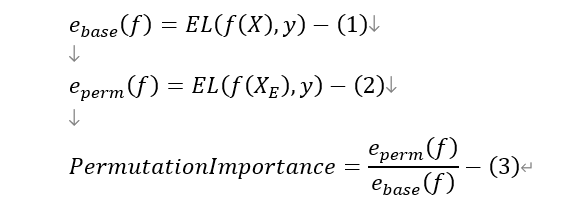
하나씩 설명 해보겠다.(L: 손실함수 E: 평균(앙상블 전체의 평균을 의미)
(1) 먼저, 기본적인 베이스라인 예측 오차를 계산한다.
(2) Randomly shuffle 한 예측 오차를 계산한다
(3) 이둘을 비율로써 나타낸다.
(4) (1)~(3)의 계산을 모든 Feature에 대해서 수행해 모델 f의 Feature Importance를 출력한다

장점

• 직관적으로 단순하다 -> 단순한 표현 방식으로 이해하기 쉽다
• 일관된 Feature의 중요도
• 재학습 불필요 -> 모델의 재학습이 불필요하고 중요도를 고속으로 산출할 수 있다.

주의할점

• 정렬의 무작위성에 의존한다. -> 계산을 반복해서 평균을 구한다면 안정된 결과를 얻을 수 있지만 그만큼 시간이 길어진다.
• 동일 성향을 가진 Feature에 의해 보충된다 -> Multicollinearity[다중공선성]에 영향을 받아 오차를 완화시켜 중요도가 낮게 산출될 수 있다.
• 주효과와 상호작용 효과를 구분할 수 없다 -> Feature Importance를 산출할 때 예측값을 사용하기 때문에 다른 Feature들의 상호작용으로 randomly Shuffle을 시킨 Feature의 효과를 낼 수도 있다

다음 포스팅인 IG는 논문을 딥하게 읽었기에 Paper Review와 이곳 두곳에 올리겠다 !