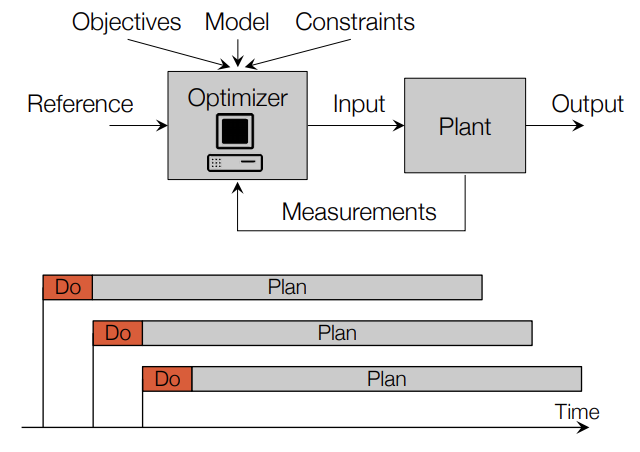
1. MPC structure
-
경로를 계산할 Plant의 model과 plant가 만족해야하는 constraint들을 설정
-
매 step마다 최적화 알고리즘을 통해 cost function이 최소가 되는 plan을 계산
-
계산한 plan의 첫번째 control action을 실행하고 반복
2. Model
x=[xyvψδ]T
u=[aω]T
- 편의상 2D Kinematic bicycle model 사용
x˙=vcosψy˙=vsinψv˙=aψ˙=vLtanδδ˙=ω
- state-space representation
x˙=Ax+Bu
A=⎣⎢⎢⎢⎢⎢⎡0000000000000000000000000⎦⎥⎥⎥⎥⎥⎤
2. Constraints
∣a∣≤amax∣δ∣≤δmax∣ω∣≤ωmax
- equality constraints
vehicle model
3. Cost function
min(x−xref)TQ(x−xref)+uTRu
Q=⎣⎢⎢⎢⎢⎢⎡q1100000q2200000q3300000q4400000q55⎦⎥⎥⎥⎥⎥⎤R=[r1100r22]
- Q 와 R 은 각 항목에 대한 weight 값 -> tuning이 필요함
4. Solver
\min {x(\cdot),u(\cdot),p} & & \int_{t_0}^{t_0 + T} \\ \Vert h( t, x(t), u(t), p ) - \eta(t) \Vert_Q^2 \; \mathrm{d}t + \Vert m( x(t_0+T), p, t_0+T ) - \mu \Vert_P^2 \\ \textrm{subject to:} & & x(t_0) = x_0 \\ \forall t \in [t_0, t_0 + T]: & & 0 = f( t, x(t), \dot x(t), u(t), p ) \\ \forall t \in [t_0, t_0 + T]: & & 0 \geq s( t, x(t), u(t), p ) \\ & & 0 = r( x(t_0+T), p, t_0+T )

