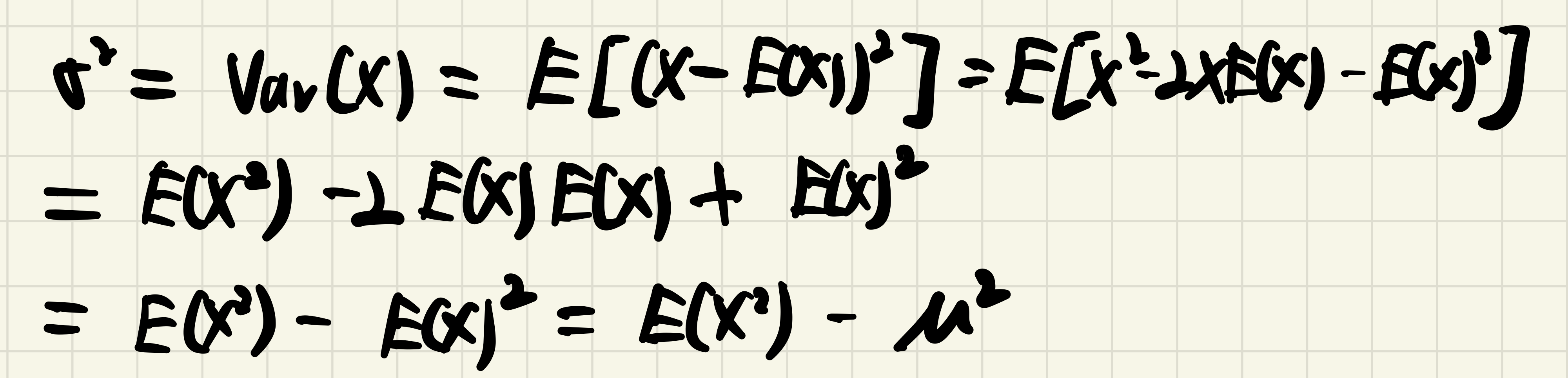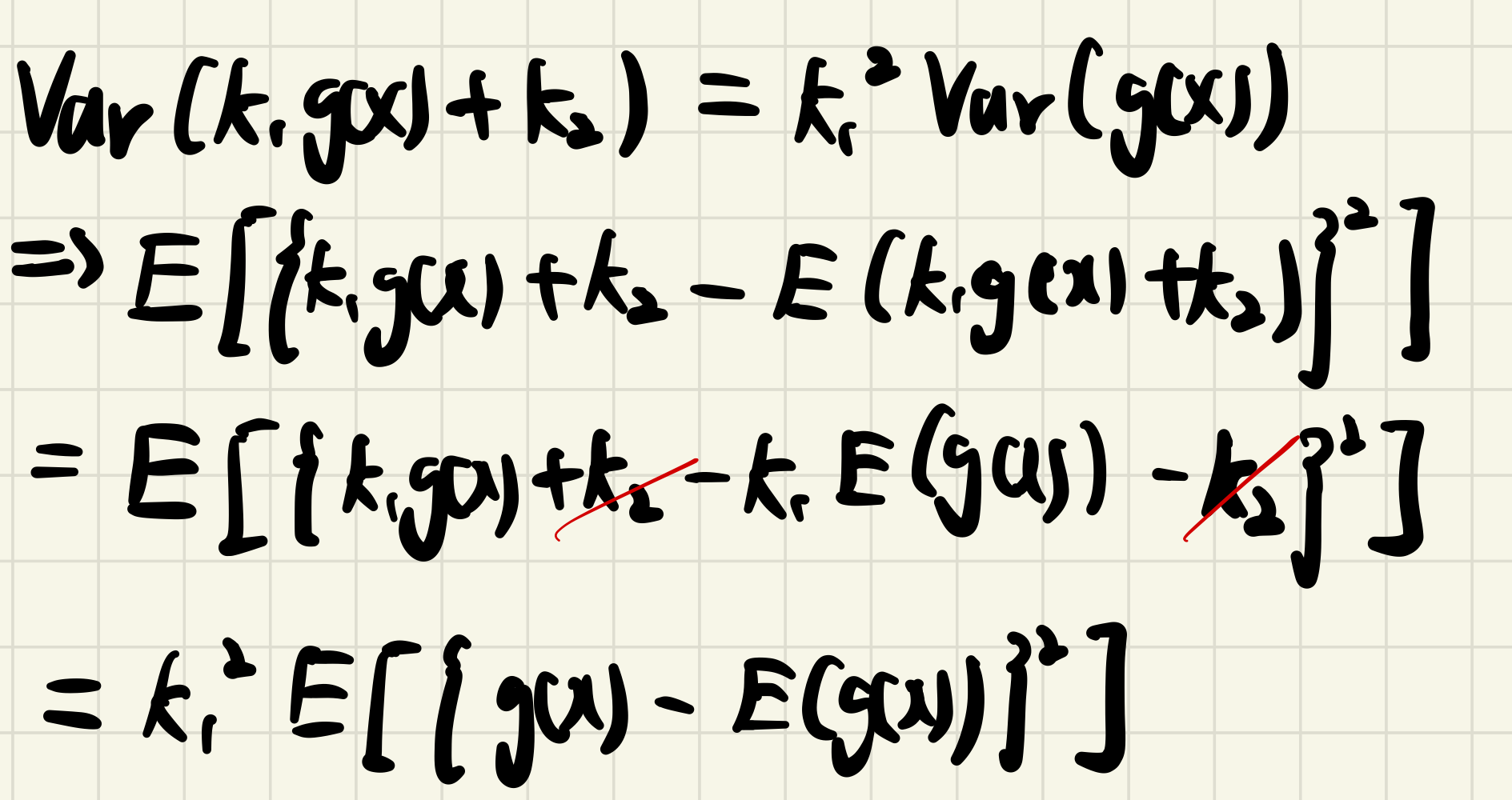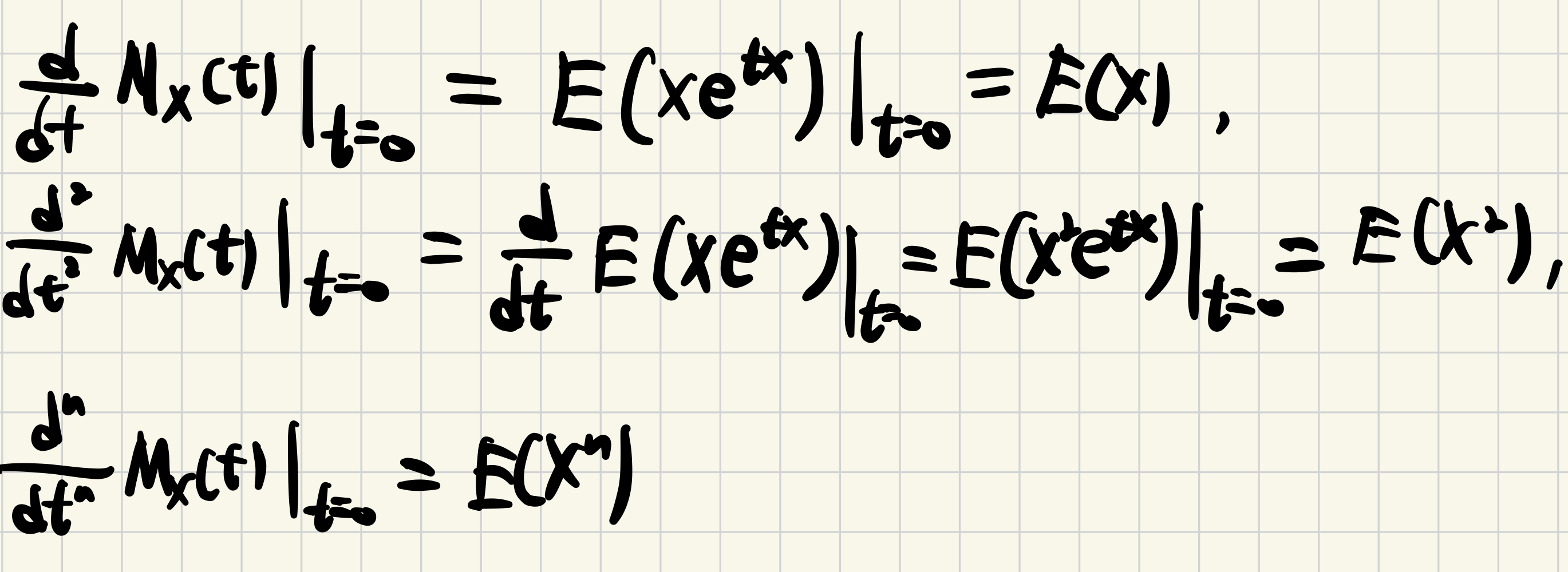Expectation of a R.V.

Def)
$E(X)=\left\{\begin{matrix} \int_{-\infty}^{\infty}xf_X(x)dx \space :continuous \\ \sum_{x}xP_X(x) \space : discrete \end{matrix}\right.$

provided $\int_{-\infty}^{\infty}|x|f_X(x)dx<\infty(or \space \sum_{x}|x|P_X(x)<\infty)$

Theorem)
If $E(g_1(x)),E(g_2(x))$ exist,
$E[k_1g_1(x)+k_2g_2(x)]=k_1E(g_1(x))+k_2E(g_2(x))$

Some special Expectations

Mean(First Moment)

The mean of $X$: $\mu=E(X)$

Variance(Second Central Moment)

The variance of $X$: $\sigma^2=Var(X)=E[(X-E(X))^2]=E(X^2)-[E(X)]^2$
pf)

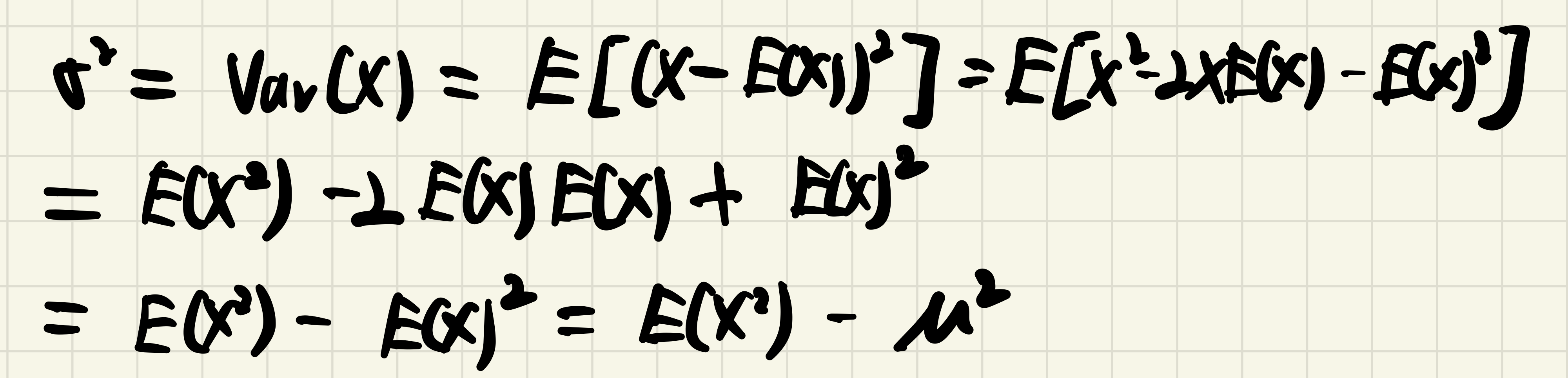
Theorem)
$Var(k_1g(x)+k_2)=k_1^2Var(g(x))$
pf)

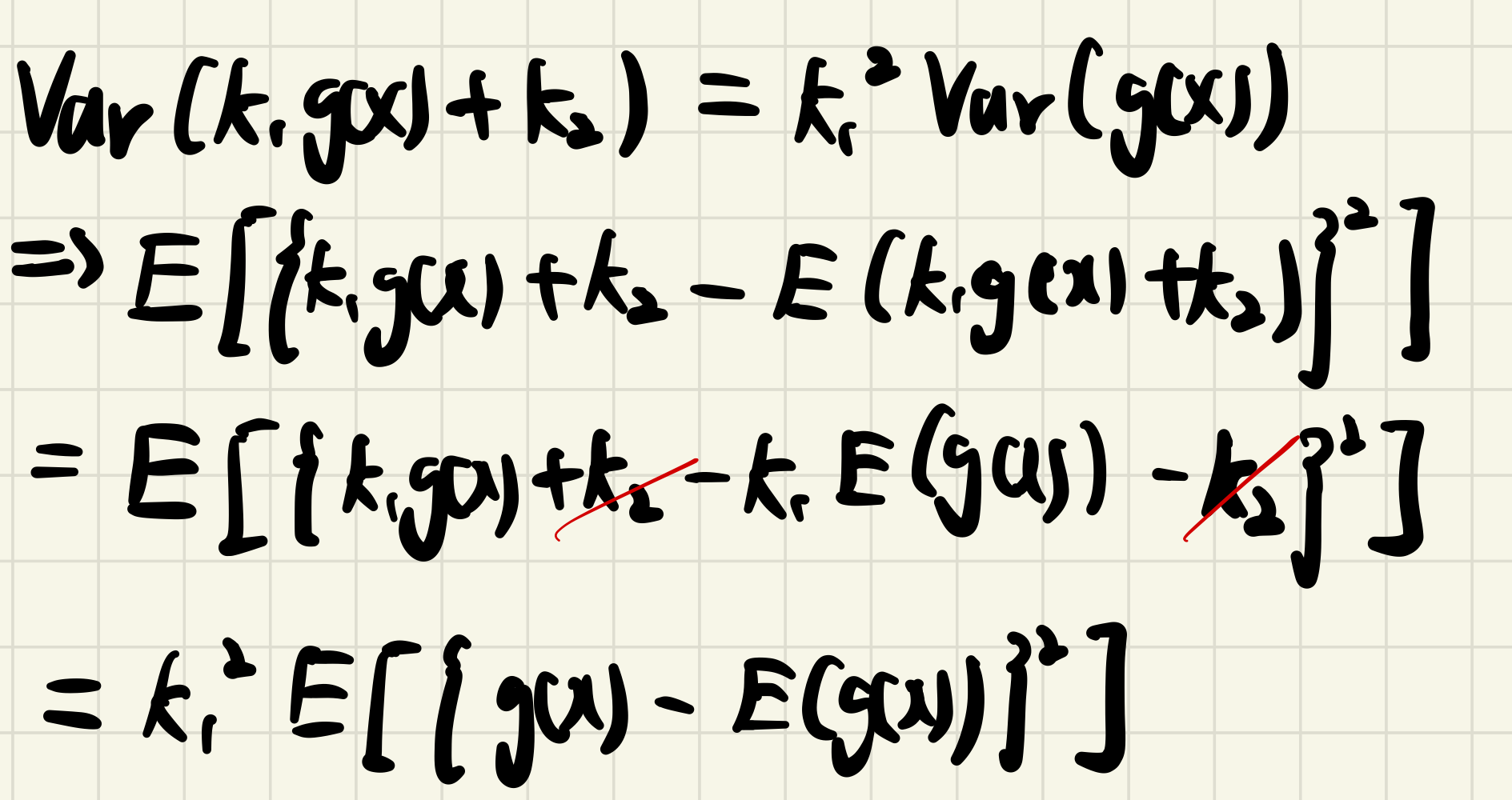
MGF(Moment Generating Function)

Def)
확률변수 $X$에 대해, $-h<t<h$ 에서 $E(e^{tx})$가 존재한다면,
$M_X(t)=E(e^{tx})$

활용법)
① mgf는 t=0 에서 n번 미분을 함으로써, n th moment of $X$를 생성한다.

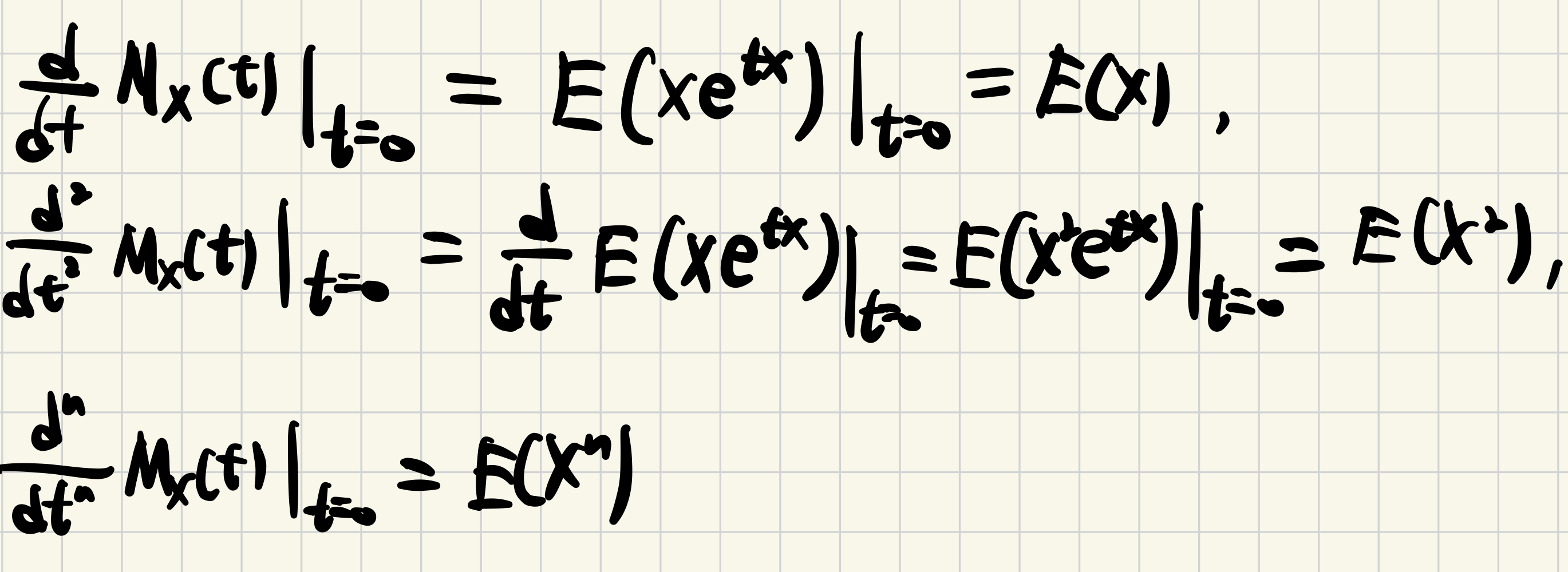
② For a certain distri., mgf is unique.
=> 두 개의 확률변수가 같은 분포를 가지는지 확인하기 위해 사용

✔︎ 주의사항
$E(X^n)(n=1,2,...):$ The n th moment of $X$
$E((X- \mu)^n)(n=1,2,...):$ The n th central moment of $X$

Multivariate case

Suppose bivariate case, $\underline{X}=(X_1,X_2)$

$E(g(X_1,X_2)) = \left\{\begin{matrix} \sum_{x_1} \sum_{x_2} g(x_1,x_2) P_{X_1,X_2} (x_1,x_2):discrete\\ \int_{-\infty}^{\infty}\int_{-\infty}^{\infty} g(x_1,x_2) f_{X_1,X_2} (x_1,x_2):continuous \end{matrix}\right. \\if \space E(g(X_1,X_2))<\infty$

Therem)
If $E(g(x_1,x_2))$ and $E(g(x_1,x_2))$ exist,
$E[k_1g_1(x_1,x_2) + k_2g_2(x_1,x_2)] = k_1E(g_1(x_1,x_2) ) + k_2E(g_2(x_1,x_2))$ for any constants $k_1$ and $k_2$

$M_{\underline{X}} (\underline{t}) = M_{X_1,...,X_n} (t_1,...,t_n)=E(e^{\underline{t}^T \underline{X}}) = E(e^{\sum_{i=1}^{n} t_i x_i})$

$E(X_1^{m_1}...X_n^{m_n})=\frac{ \partial^{m_1+...+m_n} }{\partial t_1^{m_1} ... \partial t_n^{m_n}} M_{\underline{X}} (\underline{t}) \left.\begin{matrix} \end{matrix}\right|_{ \underline{t}=0 }$

bivariate case)
$M_{X_1,X_2} (t_1,t_2) = E(e^{t_1 x_1 + t_2 x_2})$
$E(X_1^{m_1} X_2^{m_2}) = \frac{ \partial^{m_1 + m_2} }{ \partial t_1^{m_1} \partial t_2^{m_2}} M_{X_1,X_2}(t_1,t_2) \left.\begin{matrix} \end{matrix}\right|_{t_1=t_2=0}$
$M_{X_1,X_2} (t_1,0) = E(e^{t_1 x_1 + 0 x_2}) = E(e^{t_1 x_1}) = M_{X_1} (t_1)$