
- 지난 시간, 우리는 어떻게 classifier를 정의하는지 살펴봤음
- 입력이 x이고, 가중치 W를 파라미터로 갖고 있는 함수 f
- 출력은 분류하고자 하는 클래스들에 대한 score vector
- 또한, loss function을 정의할 수 있음
- SVM loss function을 예로 들면, total loss항을 정의하여 score vector가 적절한지 아닌지를 판단할 수 있음
- 여기서 loss function은 데이터 항의 조합으로 이루어져 있는데, 정규화 항을 포함하고 있음
- 정규화 항은 얼마나 우리 모델이 단순한지, 더 나은 일반화를 위해 적합한 단순 모델을 가지고 있는지를 표현해줌
- 또한, 우리는 최적의 loss를 갖게 하는 파라미터 W를 찾고 싶음
- 그래서 loss function의 W에 관한 gradient를 찾았음

- 이전 강의에서 어떻게 optimization을 사용해서 구할 수 있는지 이야기함
- gradient가 음수인 방향(즉, 경사가 하강하는 방향)을 반복적으로 구해서 아래로 나아갈 수 있고, 최종적으로는 가장 낮은 loss를 찾게 될 것임
- 경사 하강법(gradient descent)이 오른쪽 이미지와 같은 궤도를 나타내는 것을 볼 수 있음

- gradient를 구하는 다른 방법에 대해서도 살펴봤음
- 수학적으로 유한 차분 근사를 이용해 계산할 수 있음
- 이 방법은 느리고 근사치이긴 하지만, 손으로 써내려가면서 하기에는 가장 쉬운 방법임
- analytic gradient를 사용하는 것은 빠르고 정확하지만, 실수하기 쉬움
- 실제 우리가 원하는 것은 analytic gradient를 유도하고 사용하는 것임
- 동시에 수학적인 검증이 필요함
- 수학적으로 유한 차분 근사를 이용해 계산할 수 있음
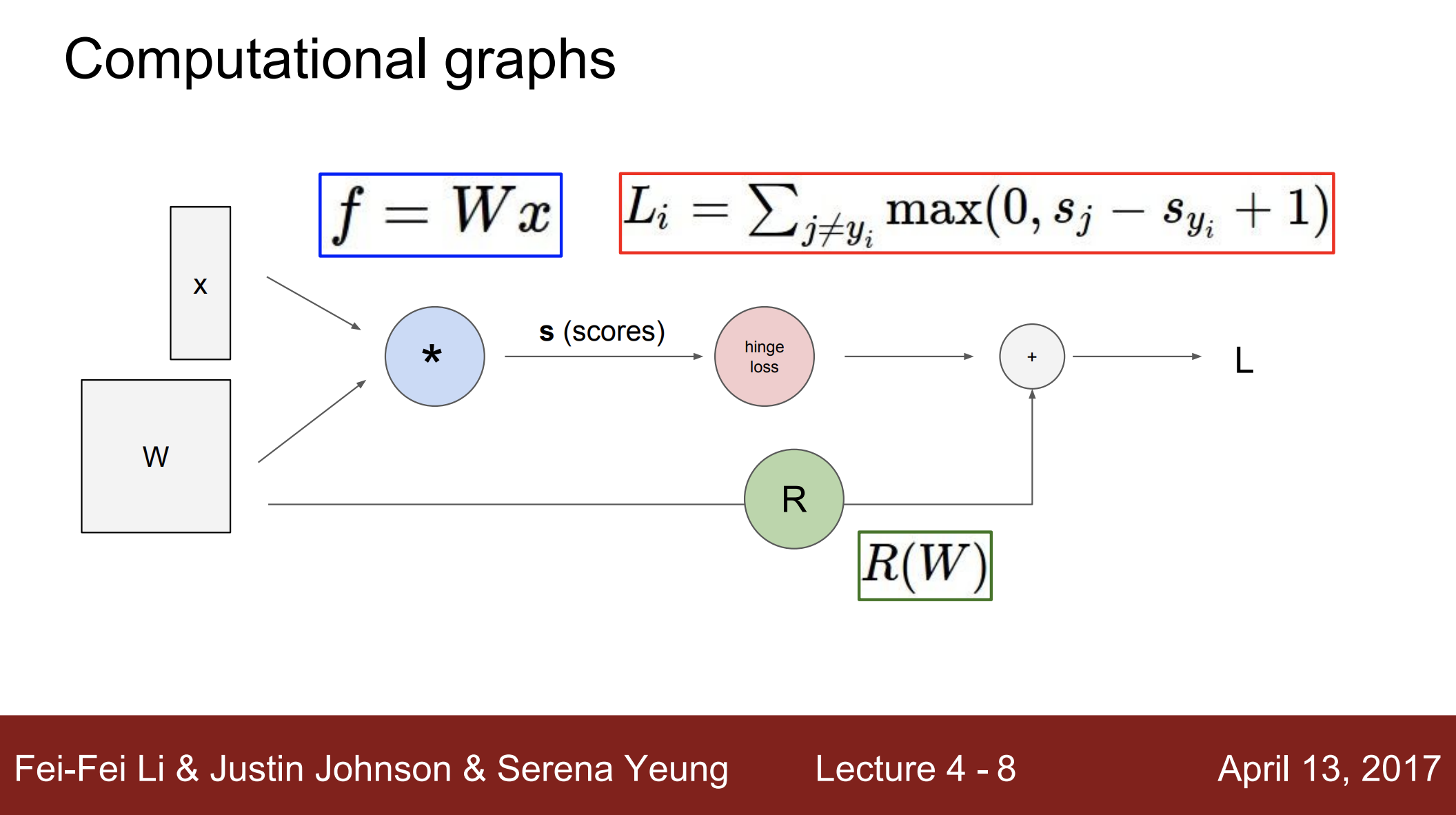
- computational graph라는 프레임워크를 사용하여 analytic gradient를 계산함
- computational graph를 이용해서 어떤 함수든 표현할 수 있음
- 각 노드는 연산 단계를 나타냄
- 위 예제는 input이 x, W인 linear classifier
- 두 input x, W를 곱하여 score vector를 출력
- 이후 hinge loss를 통해 score vector의 loss를 계산
- loss 계산 과정에서, regularization 항도 존재함
- 따라서, 최종 loss는 regularization 항과 데이터 항의 합
- computational graph를 사용하여 함수를 표현하게 됨으로써, backpropagation을 사용할 수 있게 되었음
- backpropagation은 gradient를 얻기 위해 computational graph 내부의 모든 변수에 대해 chain rule을 재귀적으로 사용함
- 이는 우리가 매우 복잡한 함수를 이용하여 작업할 때 유용하게 사용됨
- backpropagation은 gradient를 얻기 위해 computational graph 내부의 모든 변수에 대해 chain rule을 재귀적으로 사용함
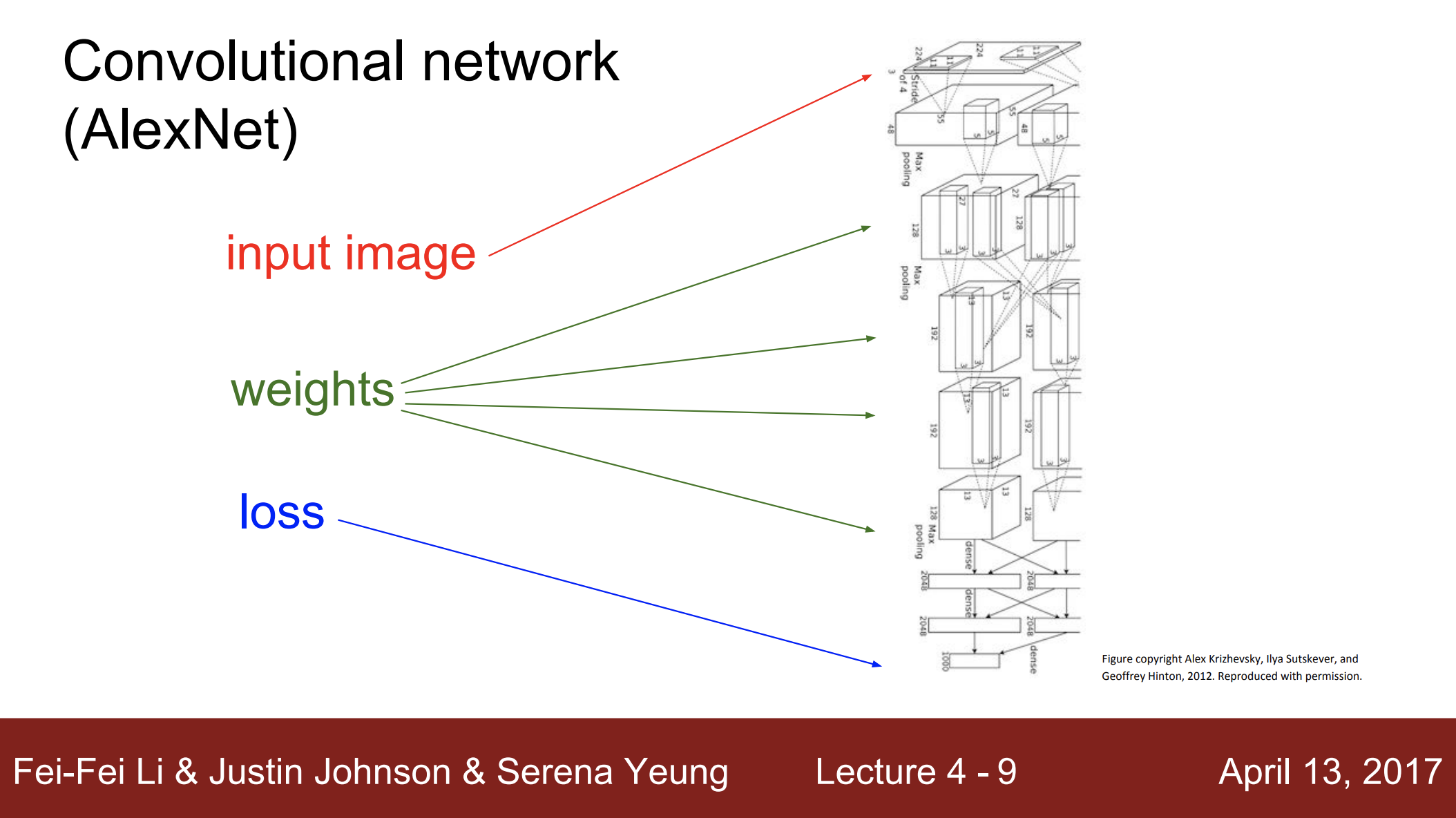
- computational graph를 사용하게 되면, 매우 복잡한 함수를 이용하여 작업할 때 유용함
- 예를 들면, 우리가 앞으로 볼 CNN은 위와 같이, 가장 윗층에 input image가 들어가고, 아래에는 loss가 존재함
- input image는 loss function으로 가는 과정에서, 많은 layer를 거쳐 변형을 겪음
- 이때 거치는 layer는 매우 많을 수도 있음 (Neural Turing Machine과 같은 모델)
- 이러한 과정을 풀기 위해서, computational graph를 사용하면 좋음
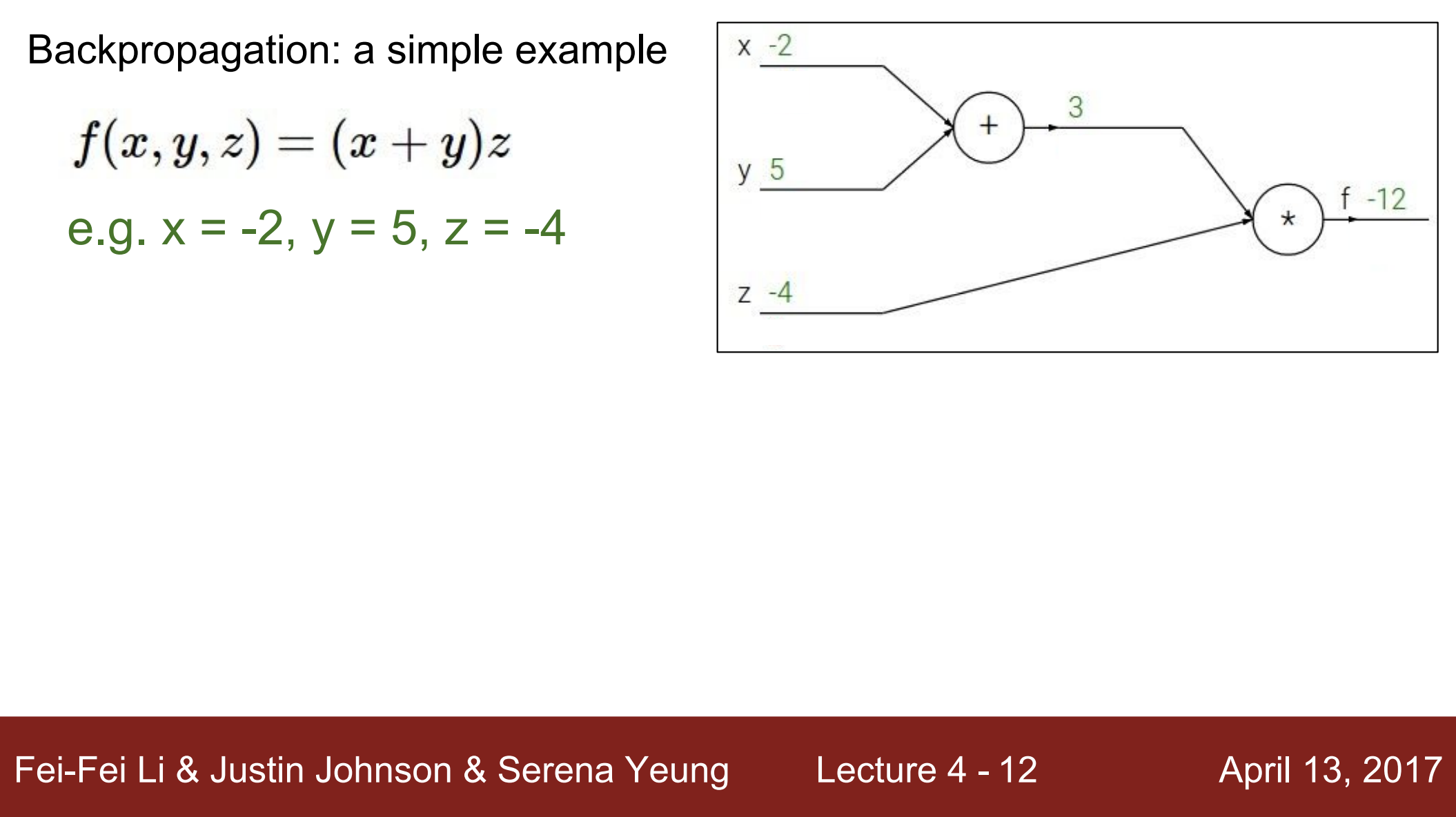
- backpropagation의 간단한 동작 과정은 다음과 같음
- 우리에게 주어진 함수는
- 우리는 이 함수 f의 출력에 대한 변수의 gradient를 찾길 원함
- 우리에게 주어진 함수는
- 첫 번째 단계는 함수 f를 computational graph로 표현하는 것
- 해당 graph를 보면, 덧셈과 곱셈 노드가 존재함
- 초기
- 중간 계산 값들은 해당 노드 옆에 적었음

-
중간에 존재하는 변수들에 이름은 q로 설정
- 즉, , 로 표현함
- 에 대해서 살펴보면,
- x, y에 대한 q의 gradient는 1 (단순 덧셈 노드이기 때문)
- 에 대해서 살펴보면,
- q, z에 대한 f의 gradient는 곱셈 규칙에 의해 각각 z와 q로 표현
-
우리가 최종적으로 찾길 원하는 것은 x, y, z에 대한 f의 gradient

- backpropagation은 chain rule의 재귀적인 응용
- 따라서, chain rule에 의해 뒤에서부터 시작함
- 먼저, computational graph의 맨 끝에서부터 gradient를 계산
- 즉, 출력에 대한 f의 gradient를 계산해야함
- 즉, 출력에 대한 f의 gradient를 계산해야함

- 이번에는 뒤로 이동해서, z에 대한 gradient를 계산
- 우리는 z에 대한 f의 미분이 q라는 것을 알고 있음
- 따라서,
- 우리는 z에 대한 f의 미분이 q라는 것을 알고 있음

- 다음으로, q에 대한 gradient를 계산
- q에 대한 f의 미분은 z임
- 따라서,
- q에 대한 f의 미분은 z임
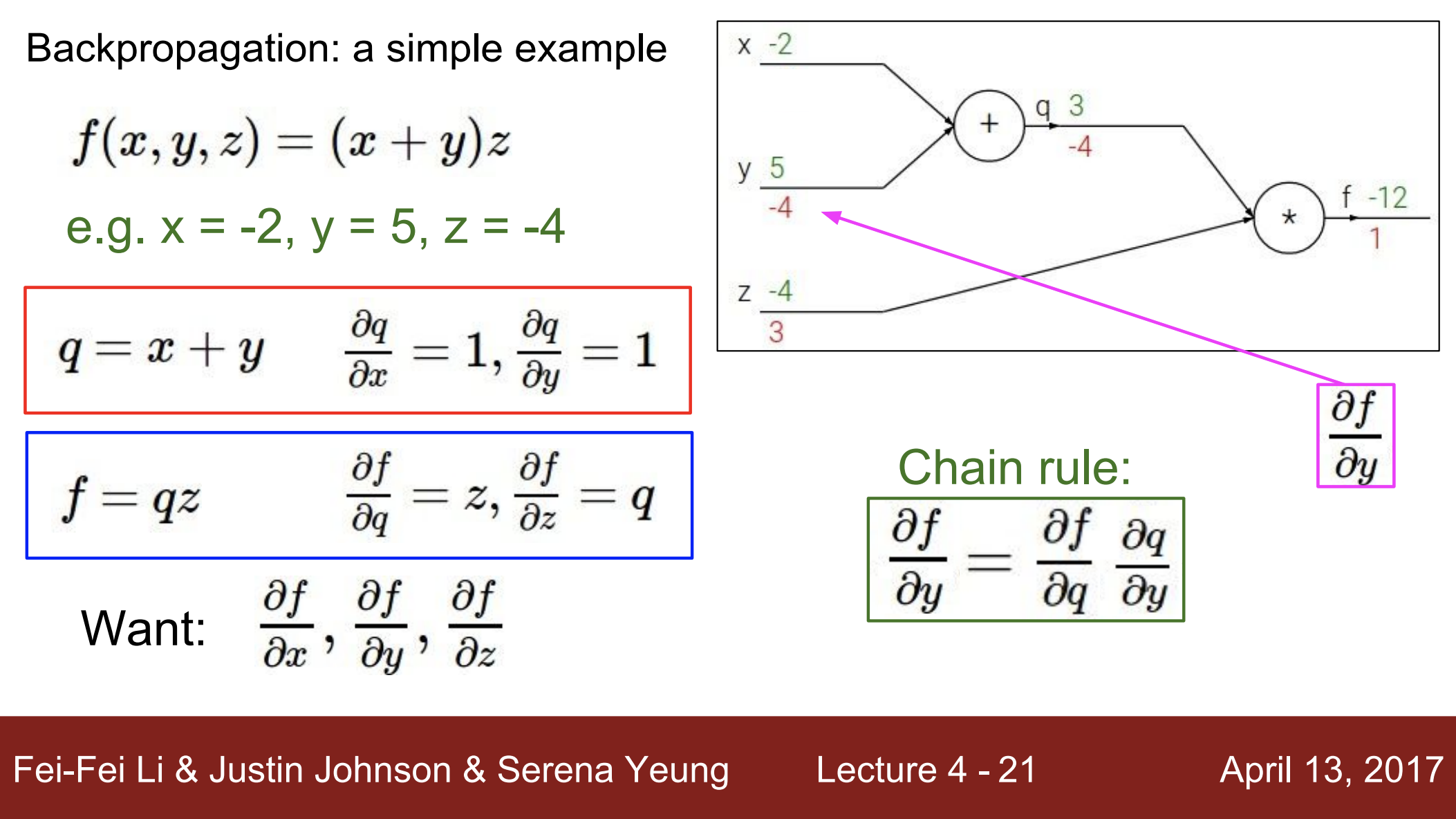
- 다시 뒤로 이동해서, 이번에는 y에 대한 gradient를 계산
- 이때 y는 f와 바로 연결되어 있지 않음
- f는 z와 연결되어 있음
- 따라서, chain rule를 이용
- 즉, 로 치환하여 계산
- 따라서,
- 이때 y는 f와 바로 연결되어 있지 않음

- x에 대한 gradient도 동일한 방법으로 계산
- chain rule에 따르면,
- 따라서,
- chain rule에 따르면,
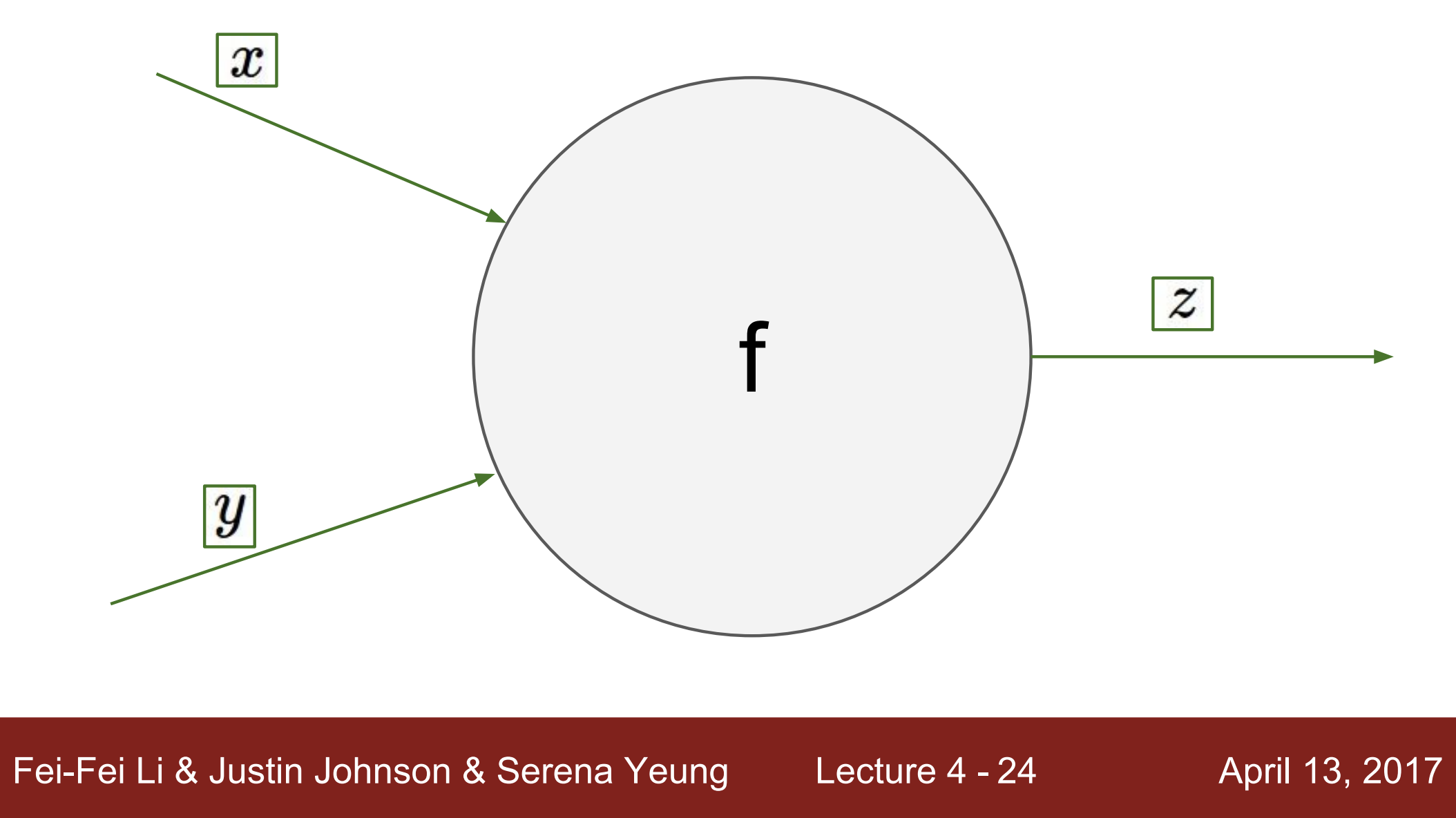
- 지금 우리가 하고 있는 backpropagation은 computational graph 안에 있는 모든 노드들을 포함하고 있음
- 하지만, 우리가 알고 있는 것은 오직 노드의 주변 정보임
- 즉, 우리가 가지고 있는 것은 각 노드와 각 노드의 local 입력
- 이러한 정보를 이용하여 출력을 만듦
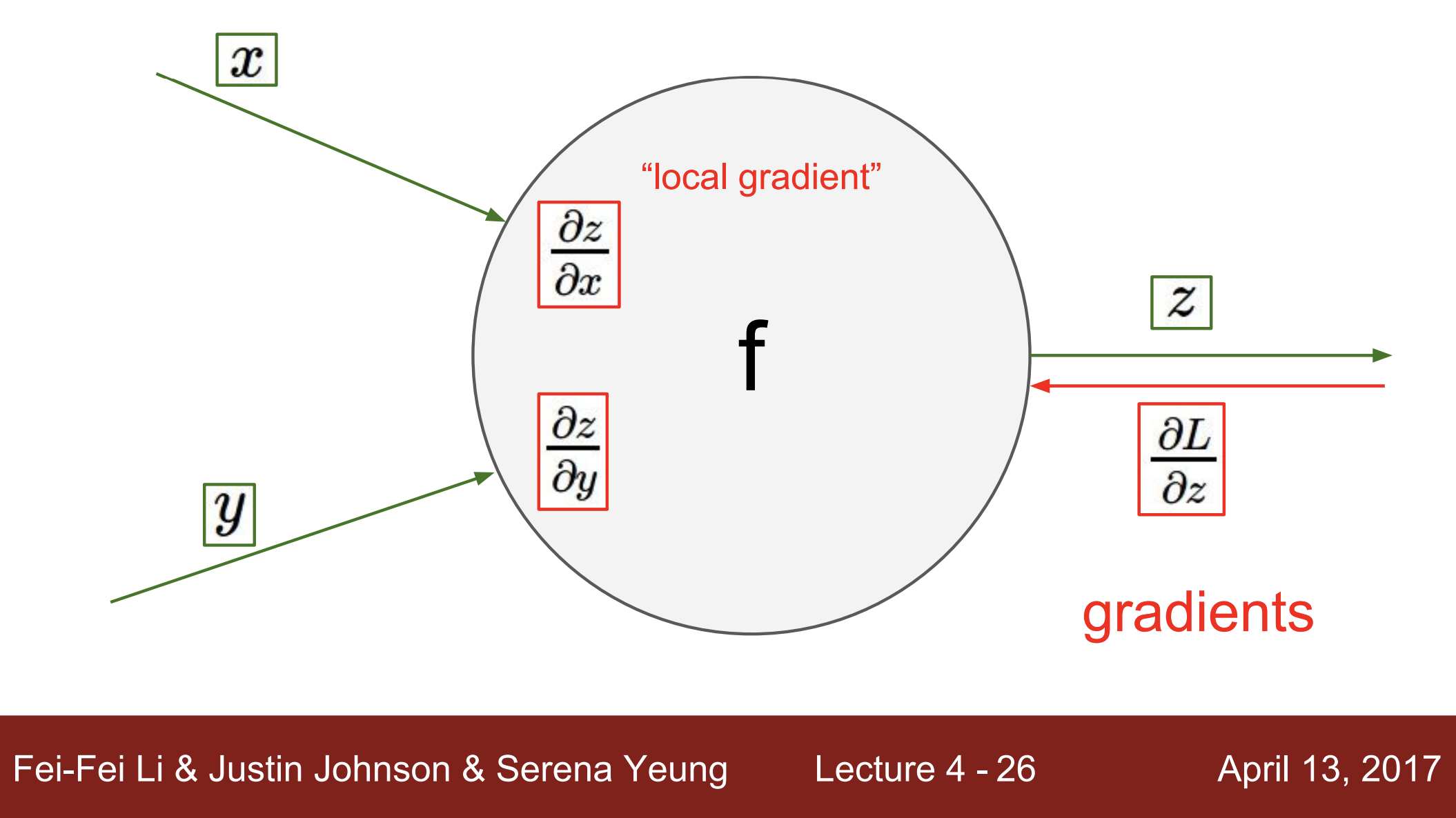
-
먼저 우리는 노드의 local gradient를 구할 수 있음 ()
- 이는 들어오는 입력에 대한 출력의 기울기
-
이때 backpropagation이 어떻게 동작하는지 살펴보면,
- 뒤에서부터 시작 부분까지 진행
- 각 노드에 도달하면, 출력과 관련한 노드의 gradient가 상류(입력과 가까운) 노드로 전파
- 따라서, 우리는 backpropagation에서 이 노드에 도달할 때까지 z에 대한 최종 loss L은 이미 계산되어 있음 ()
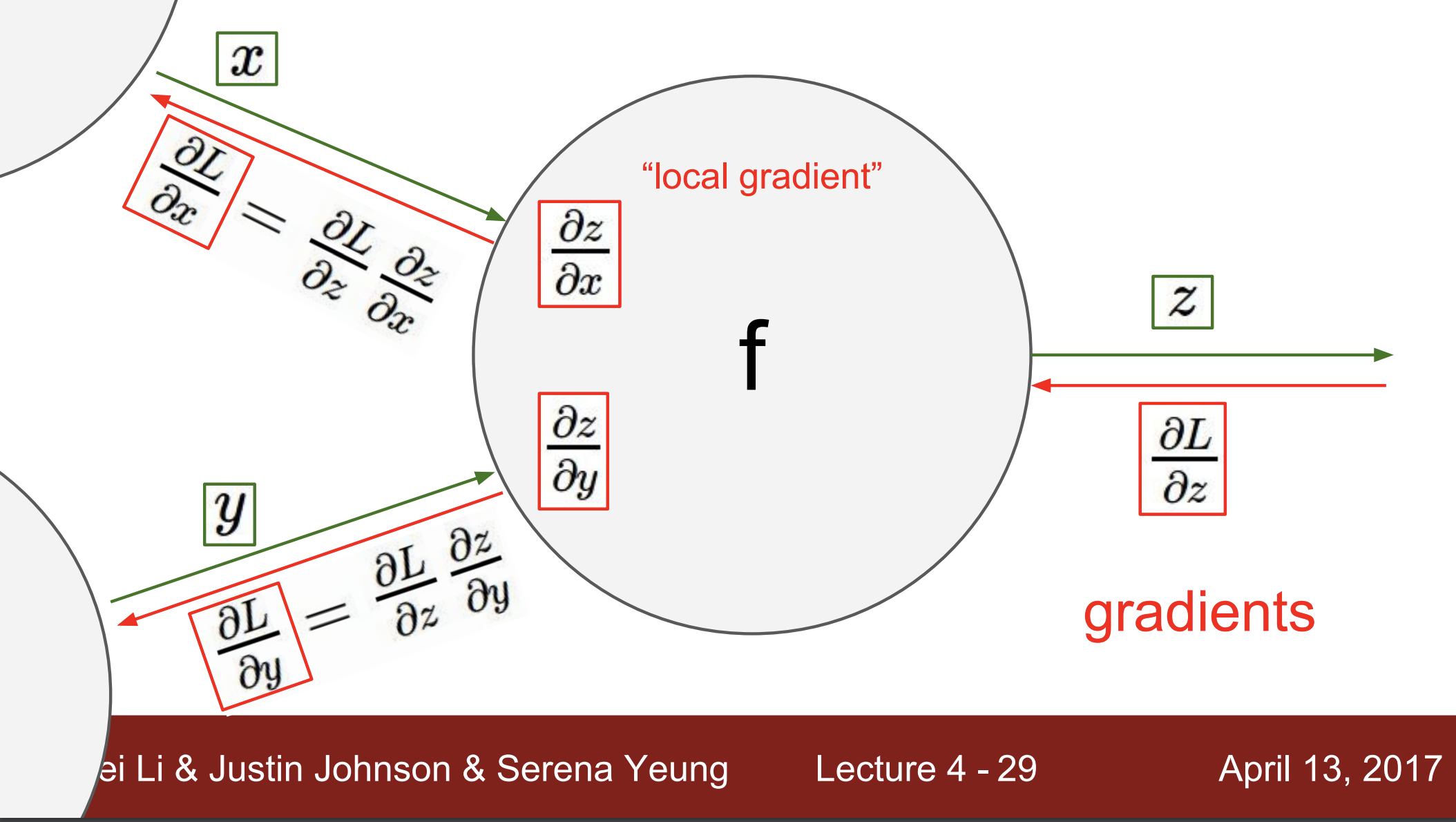
-
이제 우리는 x와 y의 값에 대한 바로 직전 노드의 gradient를 찾고자 함
- chain rule을 사용하여 local gradient를 계산
- x의 gradient()는 z에 대한 gradient()와 x에 대한 z의 gradient()로 치환
- 즉, upstream gradient와 local gradient를 곱하여 현재 입력에 대한 gradient를 계산함
- chain rule을 사용하여 local gradient를 계산
-
이후 계산된 gradient 값을 해당 노드와 연결된 상류 노드로 전달

- computational graph에서 직관적인 해석으로 알 수 있는 패턴이 존재함
- add 게이트는 gradient를 나눠줌 (distributor)
- 즉, upstream gradient를 그대로 가져옴 (local gradient가 1이기 때문)
- max 게이트는 gradient 라우터 (router)
- 즉, upstream gradient를 입력이 큰 노드로 전달하고, 다른 노드에는 0을 전달 (forward 시에 큰 값만 출력에 영향을 주기 때문에, 실제 영향을 주는 값은 둘 중 큰 값임. 따라서, 해당 값에 대한 gradient만 존재)
- mul 게이트는 gradient switcher, scaler
- 즉, upstream gradient를 받아 다른 브랜치의 값으로 scaling함
- add 게이트는 gradient를 나눠줌 (distributor)
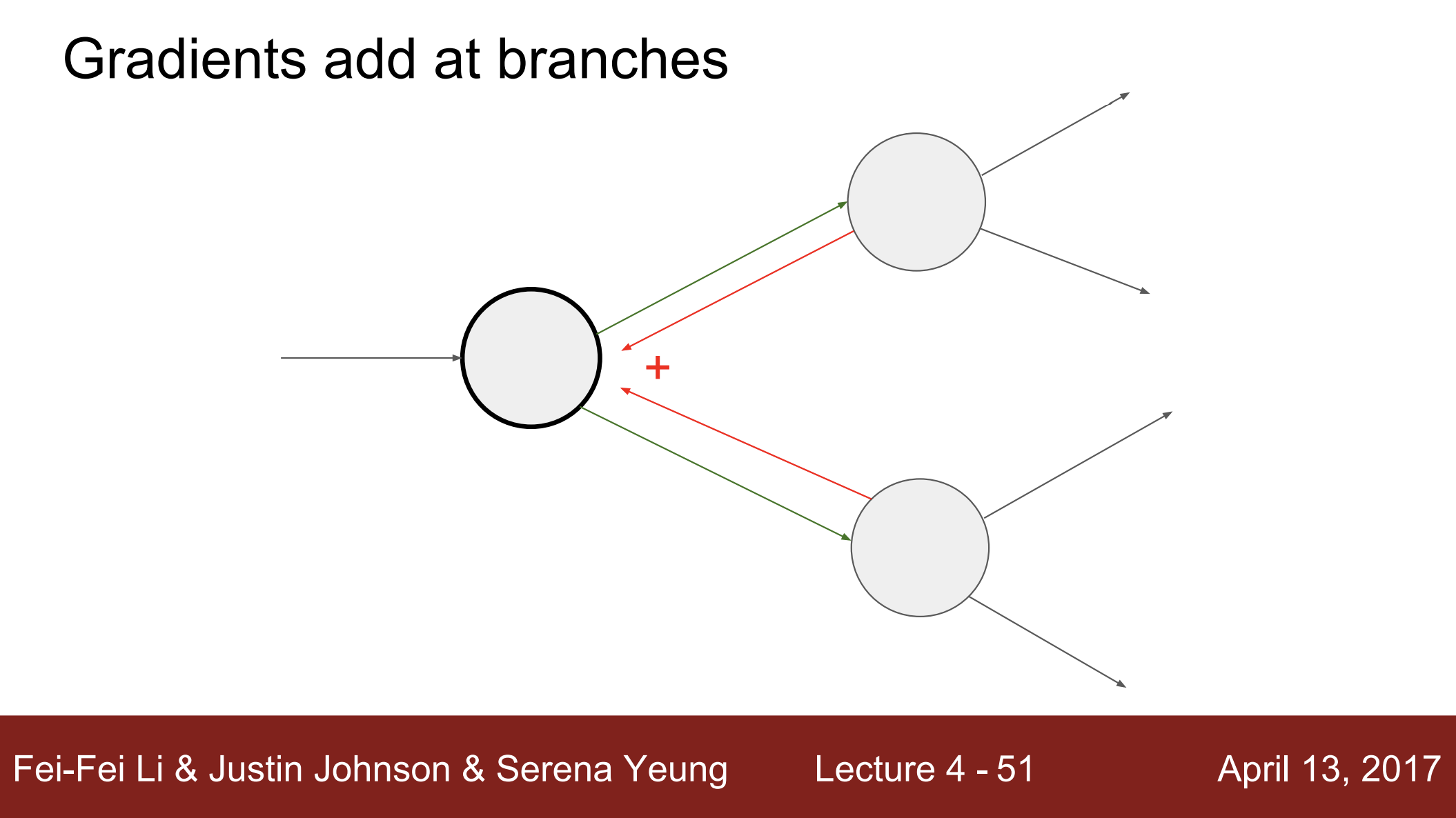
- 이번에는 두 개의 브랜치가 하나로 합쳐지는 패턴
- 이 경우, 두 개의 upstream gradient를 합쳐줌
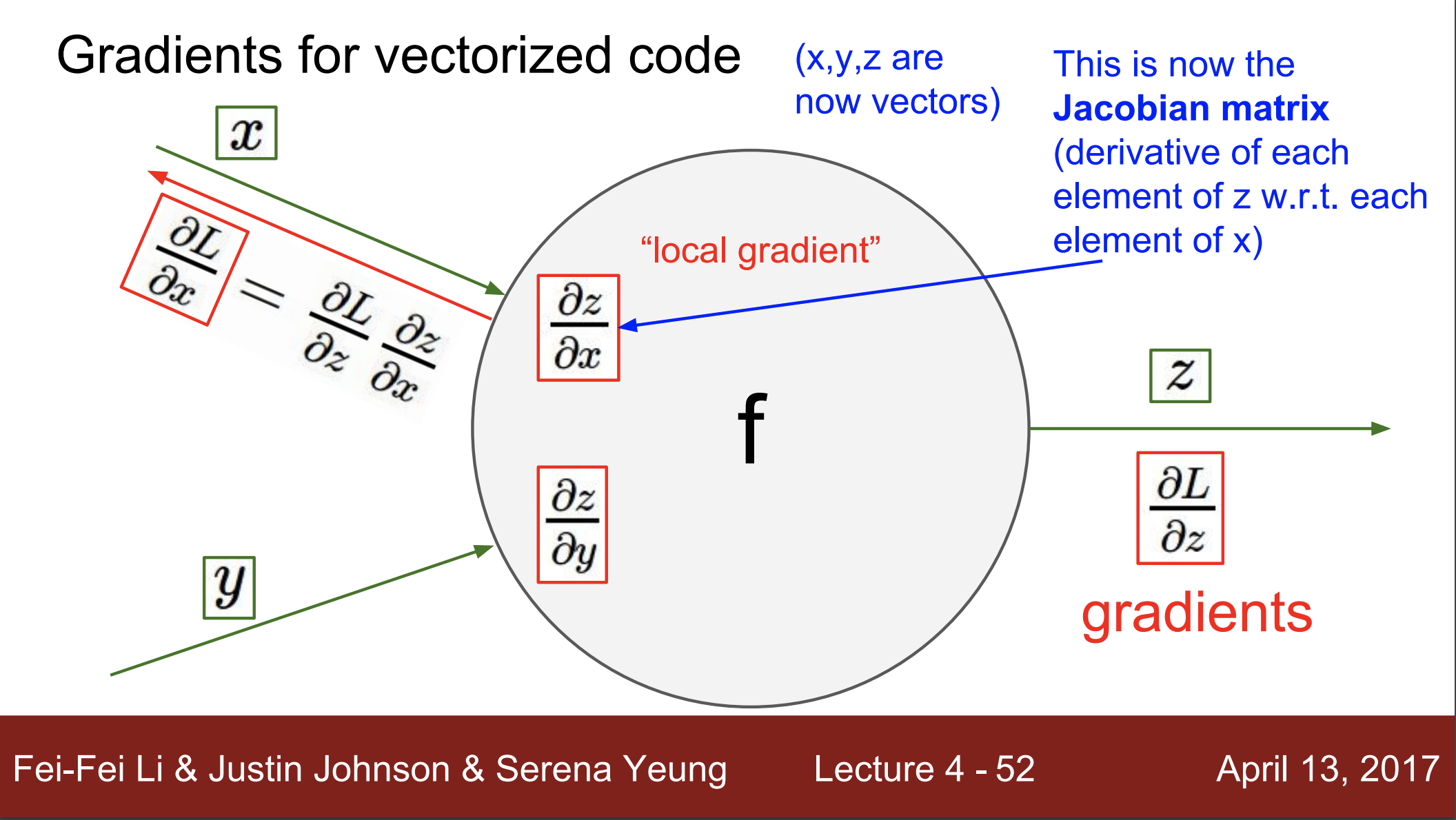
- 지금까지는 스칼라 값을 이용한 예제
- 실제로는 vector를 사용함
- 모든 흐름은 동일하지만, gradient는 Jacobian 행렬이 될 것임
- 즉, 각 요소의 미분을 포함하는 행렬
- 실제로는 vector를 사용함
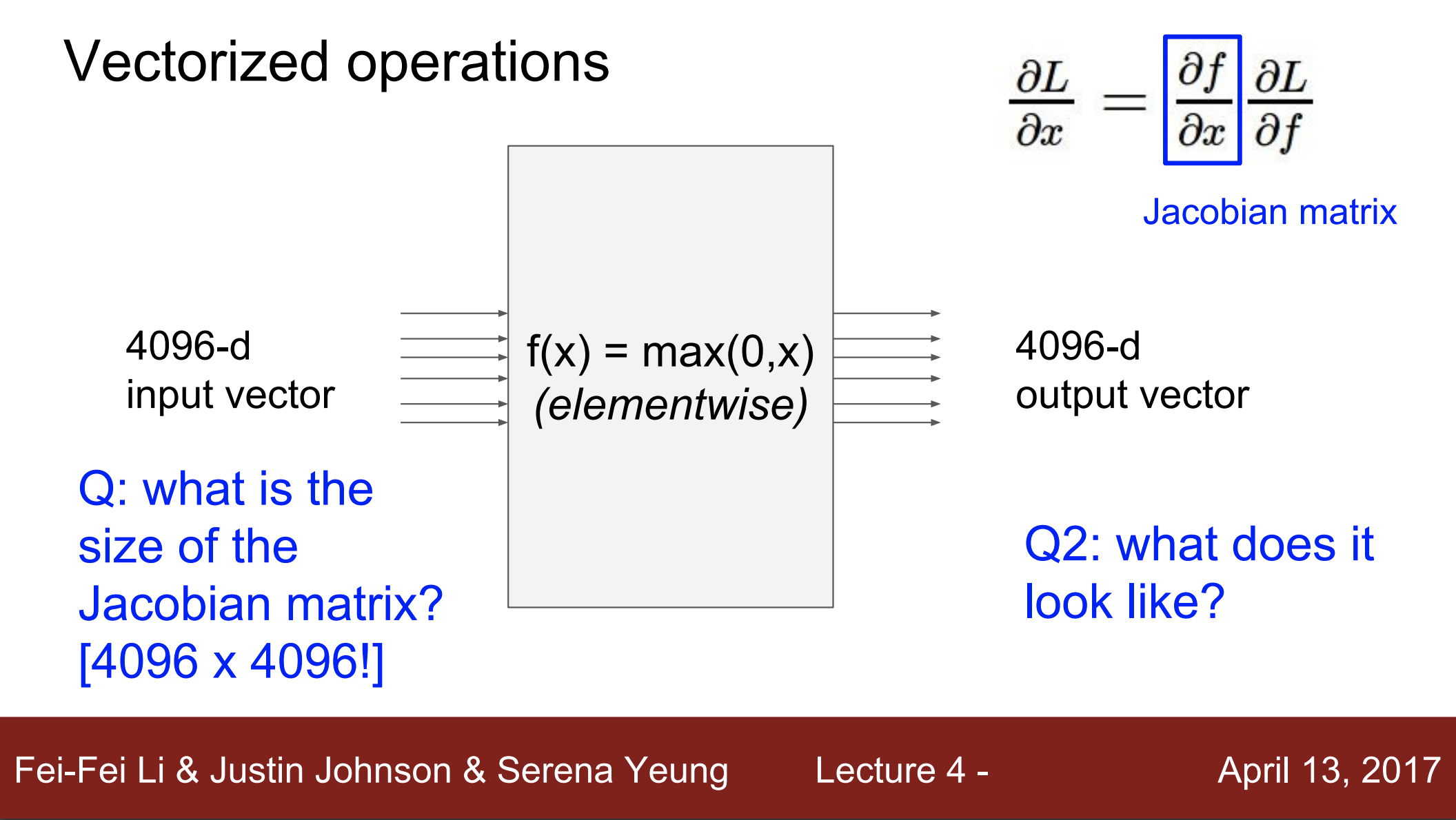
- 우리의 입력이 4096 차원이고, 요소별로 0과 비교하여 최대 값을 취하는 함수 f가 존재한다고 가정하자 (출력도 4096 차원)
- Q1. 이 경우 Jacobian 행렬의 사이즈는 얼마인가?
- Jacobian 행렬의 각 행은 입력에 대한 출력의 편미분임
- 따라서, 행렬의 크기는 4096 x 4096
- Q2. 이 Jacobian 행렬이 어떻게 생겨나게 되었을까?
- Q1. 이 경우 Jacobian 행렬의 사이즈는 얼마인가?

- 구체적인 vectorized 된 다른 예시를 보면,
- 함수
- 이때 x는 n 차원이고, W는 n*n 차원

- W는 2*2 행렬이고, x는 2차원의 vector
- 중간 곱셈 노드를 계산한 후, L2를 계산하면 위와 같음

- backpropagation을 진행하면,
- 가장 먼저, 출력에 대한 gradient를 계산
- 다음으로 한 노드 뒤로 이동하여 gradient를 계산
- L2 이전의 중간 변수인 곱셈 노드의 gradient를 계산
- [0.44 0.52]
- 가장 먼저, 출력에 대한 gradient를 계산

- 이후 W의 gradient를 계산
- 곱셈 노드이기 때문에, grdient switcher로 동작
- x의 gradient도 동일한 방법으로 계산

- 앞서 computational graph를 통해 계산한 forward pass와 backward pass를 위와 같이 API로 생각할 수 있음
- forward pass에서는 노드의 출력을 계산하는 함수를 구현
- backward pass에서는 gradient를 계산
- backward pass를 계산할 때는 chain rule을 이용

- 노드를 처리하기 전에, 이 전에 노드로 들어오는 모든 입력을 처리함
- 즉, forward pass를 순서대로 처리
- backward pass는 역순서로 모든 게이트를 통과한 다음 게이트 각각을 거꾸로 호출함

- 우리가 지금까지 이야기한 것은,
- 다양한 linear score function을 이용했음
- 해당 함수를 최적화할 때의 실행 예제로 사용했음
- 이제 2층짜리 신경망 layer를 살펴보자
- 이 함수는 아래 그림처럼 생겼음
- 즉, 중간 값()을 얻고, 이를 비선형 함수 를 이용하여 최종 출력을 얻음
- 즉, 신경망은 함수들의 집합이라고 할 수 있음
- 비선형의 복잡한 함수를 만들기 위해, 여러 간단한 함수들을 계층적으로 쌓아 올린 집합
- 다양한 linear score function을 이용했음
비선형 함수를 사용하는 것이 중요한 이유는, 선형 레이어로만 이루어진 함수는 아무리 깊게 쌓는다고 해도 결국 선형 함수일 뿐이다. 이는 결국 단순한 task만 수행이 가능하며, 복잡한 task를 수행하기 위해서는 부적합하다. 따라서, 비선형 함수를 사용하는 것이다.

- activation function은 추후에 다시 살펴볼 예정
- neural network에서 사용하는 activation function은 다은과 같음
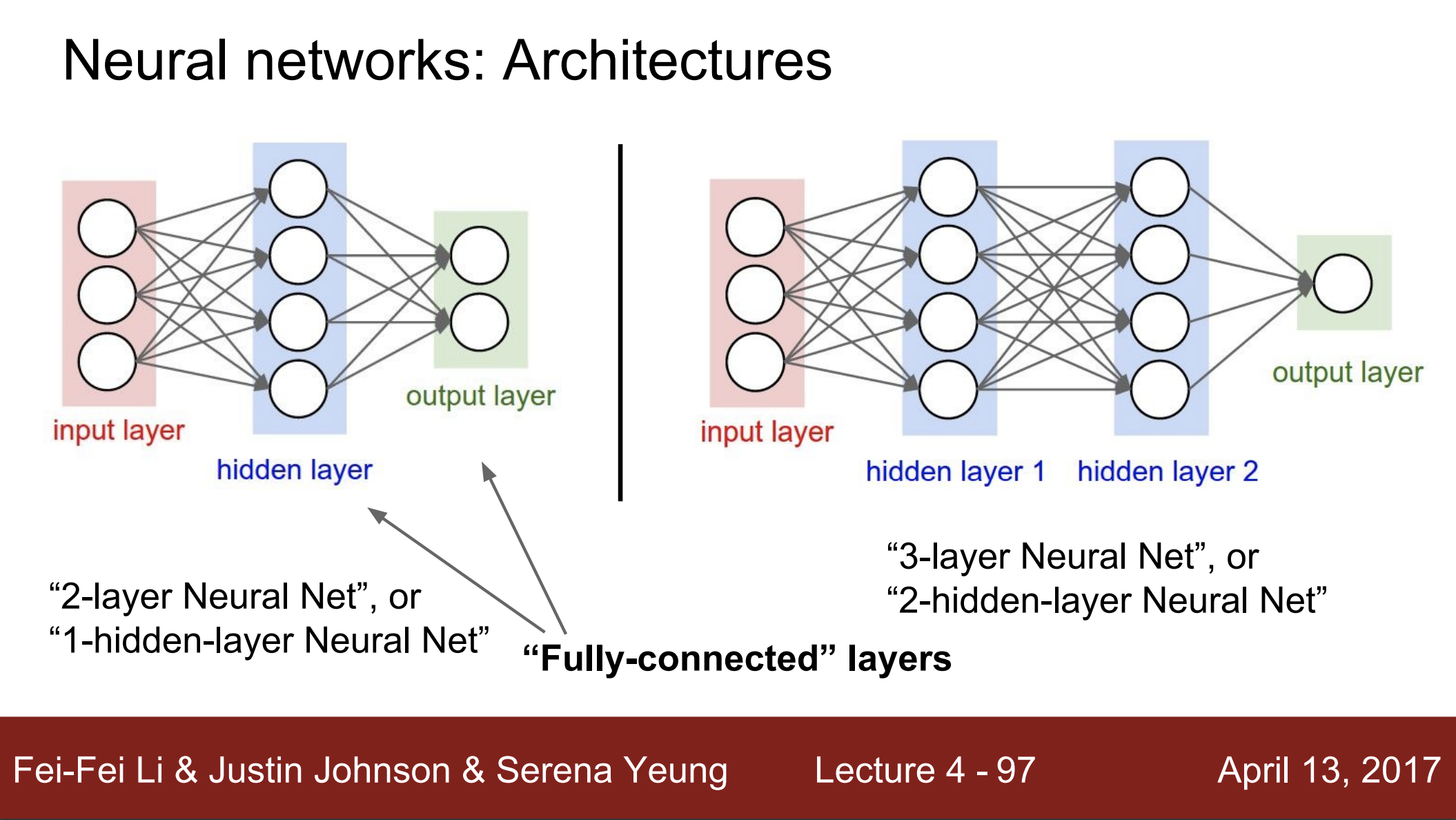
- 지금까지 우리는 완전히 연결된 신경망 예제를 보았음 (Fully Connected layer)
- 각 레이어는 행렬곱을 했음
