📈 용어정리
- 오차 : 데이터 포인트와 예측값 혹은 평균 사이의 차이
- 표준화(정규화)하다 : 평균을 빼고 표준편차로 나눈다.
- z 점수(z-score) : 개별 데이터 포인트를 정규화한 결과
- 표준정규분포(standard normal distribution) : 평균 = 0, 표준편차 =1인 정규분포
- QQ그림 : 표본분포가 특정 분포(예 : 정규분포)에 얼마나 가까운지를 보여주는 그림
📈 정규분포
- 종 모양의 정규분포는 전통적인 통계의 상징이다. 표본통계량 분포가 보통 어떤 일정한 모양이 있다는 사실은 이 분포를 근사화하는 수학 공식을 개발하는 데 강력한 도구가 되었다.
📈 정규화와 표준화
<정규화>
- 데이터 분포를 특정 구간으로 바꾸는 척도법이다.(0~1, -1~1)
- 데이터 군 내에서 특정 데이터가 가지는 위치를 볼때 사용된다.
- 식 = (측정값 - 최소값) / (최대값 - 최소값)
<표준화>
- 데이터를 0을(평균) 중심으로 양쪽으로 데이터를 분포시키는 방법(표준화를 하게 되면 각 데이터들은 평균을 기준으로 얼마나 떨어져 있는지를 나타내는 값으로 변환된다)
- 평균0 표준편차가 1
- 식(z-score표준화) : (측정값 - 평균) / (표준편차)
📈 z-score
- 데이터를 표준화한 값
📈 표준정규분포와 QQ-plot(QQ그림)
- 표준정규분포는 x축의 단위가 평균의 표준편차로 표현되는 정규분포를 말한다. 데이터를 표준정규분포와 비교하려면 데이터에서 평균을 뺀 다음 표준편차로 나누면 된다(표준화). 그리고 이렇게 변환된 값을 z-score 라고 하며, 정규분포를 z분포 라고 한다.
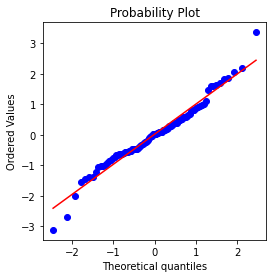
- QQ그림은 표본이 특정분포(예 : 정규분포)에 얼마나 가까운 형태인지 시각적으로 확인하기 위해서 사용된다.
- z-score를 오름차순으로 정렬후 각 값의 z-score를 y축에 표시하고 정규분포에서의 해당 분위수를 x축에 표시한다.
- 점들이 대략 대각선 위에 놓인다면 표본분포가 정규분포에 가까운것으로 간주할 수 있다.
- python에서는 scipy.stats.probplot을 통해 QQ-plot을 만들 수 있다.
fig, ax = plt.subplots(figsize = (4, 4))
norm_sample = stats.norm.rvs(size = 100)
stats.probplot(norm_sample, plot = ax)
>>>
주의할점
데이터를 z-score로 변환(즉, 데이터를 표준화 또는 정규화)한다고 해서 데이터가 정규분포가 되는 것은 아니다. 단지 비교를 목적으로 데이털르 표준정규분포와 같은 척도로 만드는 것 뿐이다.
📈 정규분포가 아닐때 QQplot예시

