https://www.youtube.com/watch?v=lIT5-piVtRw&t=215s
위 자료를 참고했다.

---

https://velog.io/@ljwljy51/Decision-Tree-Model
위 글과 내용이 이어진다.

---

Random Forest Model 배경 - Ensemble

• 앙상블이란, 여러 베이스 모델들의 예측을 다수결 법칙 혹은 평균을 이용해 예측 정확성을 향상시키는 방법이다.

• 다음 조건을 만족할 때 앙상블 모델은 베이스 모델보다 우수한 성능을 보인다.

  • 베이스 모델이 서로 독립적인 경우
  • 베이스 모델들이 무작위 예측을 수행하는 모델보다 성능이 좋은 경우
    • 이때 무작위 예측이란, 이진분류의 경우, 베이스 모델이 최소한 0.5만큼의 예측을 하는 경우에 해당

• Random Forest Model의 경우, 앙상블의 베이스 모델로 Decision Tree Model을 사용하는 것

  • Decision Tree Model의 장점
    • Low computational complexity: 데이터 크기가 방대한 경우에도 모델을 빨리 구축할 수 있음
    • Nonparametric: 데이터 분포에 대한 전제가 필요하지 않음

---

앙상블 모델의 오류율

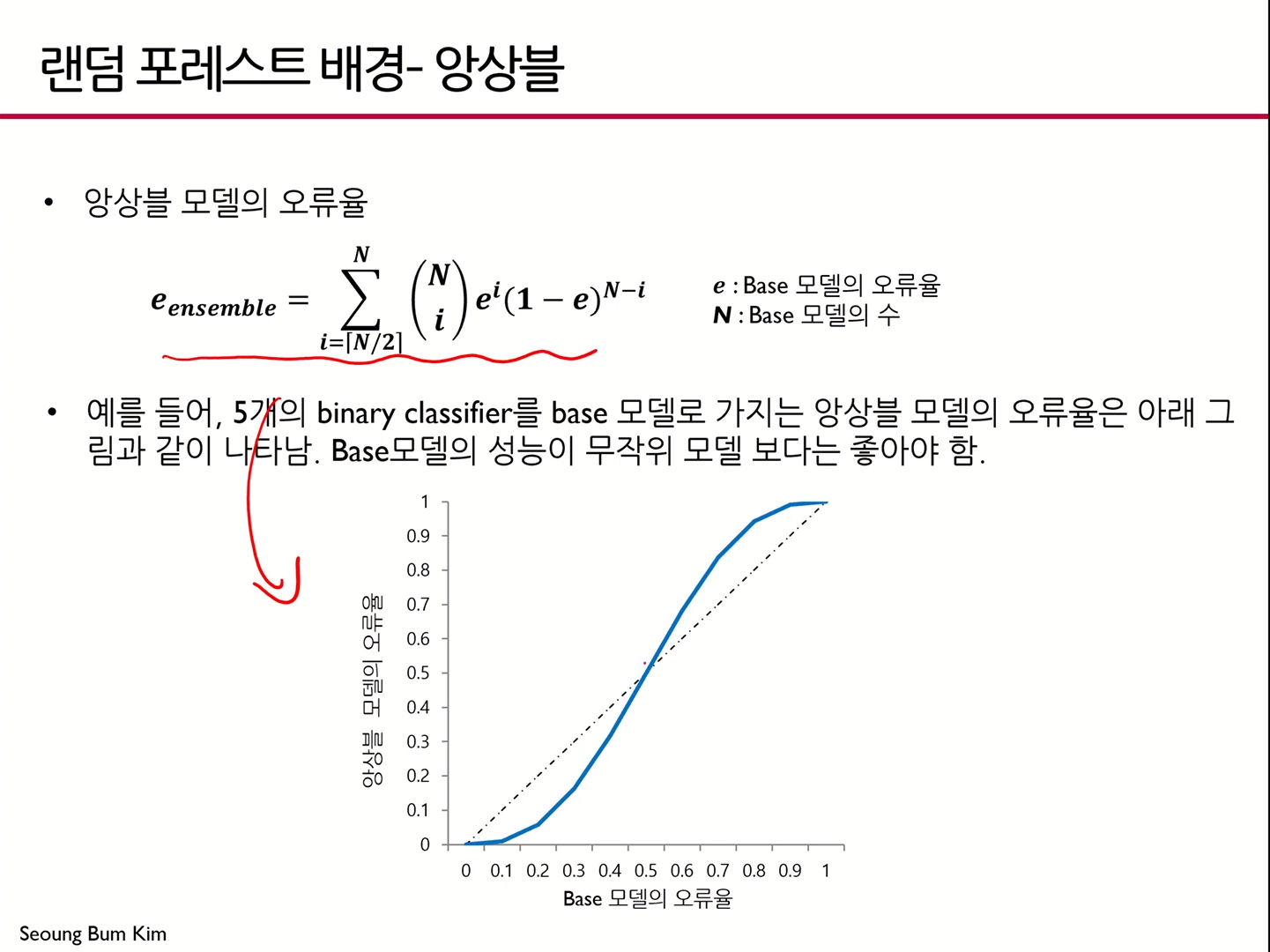
• 베이스 모델의 오류율이 0.5보다 큰 경우, 앙상블 모델의 오류율이 더 커짐
  • 앞서 언급된 가정과 연결해 생각하면 이해하기 쉬움
• 베이스 모델의 오류율이 0.5보다 작은 경우, 앙상블 모델을 썼을 때 오류율이 더 낮은 것을 알 수 있음

---

Random Forest Model 개요

• 다수의 Decision Tree Model에 의한 예측을 종합하는 앙상블 방법
• 일반적으로 하나의 Decisoin Tree Model보다 높은 예측 정확성을 보여줌
• 관측치 수에 비해 변수의 수가 많은 고차원 데이터에서 중요 변수 선택 기법으로 널리 활용됨

모델의 예측 과정은 다음과 같다.

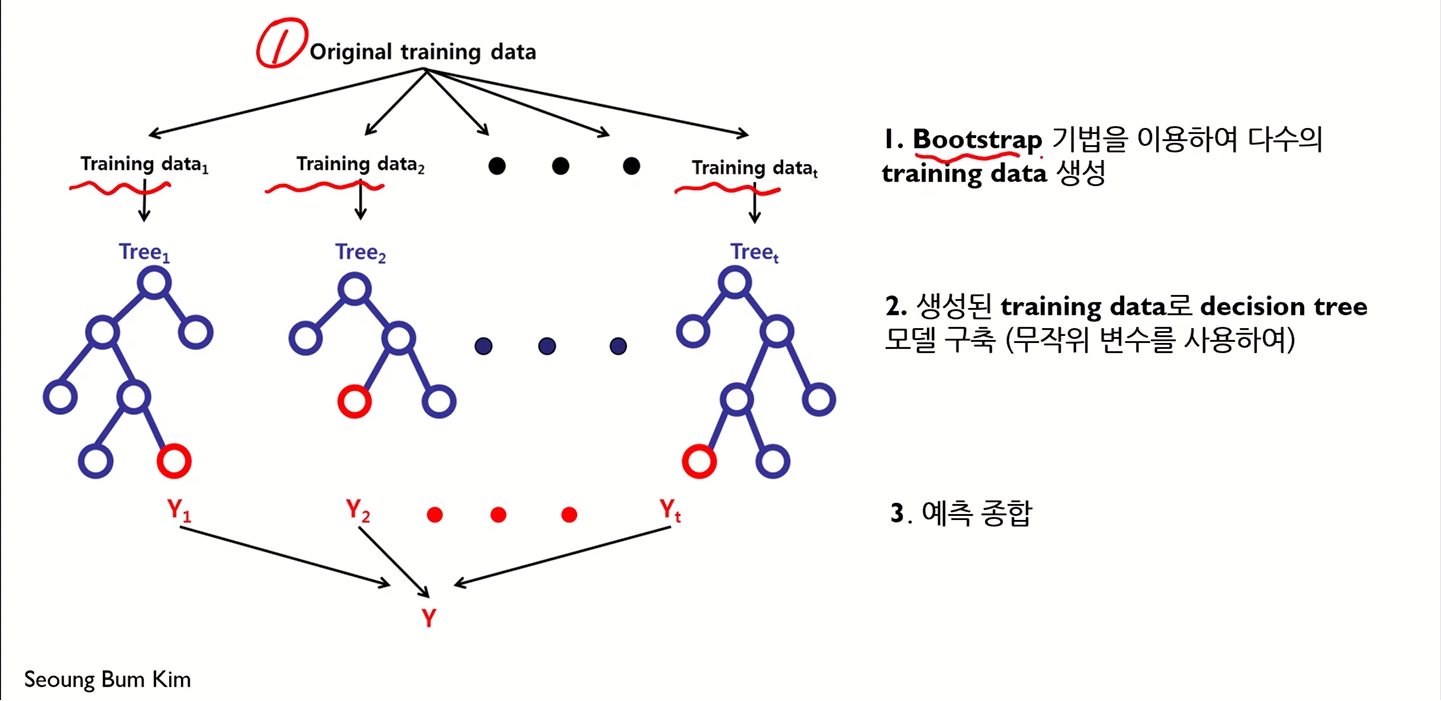
즉

• Diversity
• Random
  위 두 가지를 확보하는 것이 랜덤 포레스트 모델의 핵심 아이디어가 되는 것

여기서 두 가지 과정으로 나눌 수 있다.

• 여러 개의 Training data를 생성해 각 데이터마다 개별의사결정나무모델을 구축하는 것
  • Bagging
• 의사결정나무모델 구축 시 변수를 무작위로 선택
  • Random subspace

여기서 Bagging, Random subspace라는 두 키워드를 잘 기억해야 한다

---

Bootstrapping

• 샘플링 기법 중 하나
• 각 모델은 서로 다른 학습 데이터셋을 이용함
• 각 데이터셋은 "복원추출"을 통해 "원래 데이터의 수만큼의 크기"를 갖도록 샘플링됨
• 각 개별 데이터셋을 붓스트랩셋이라 부른다.
  

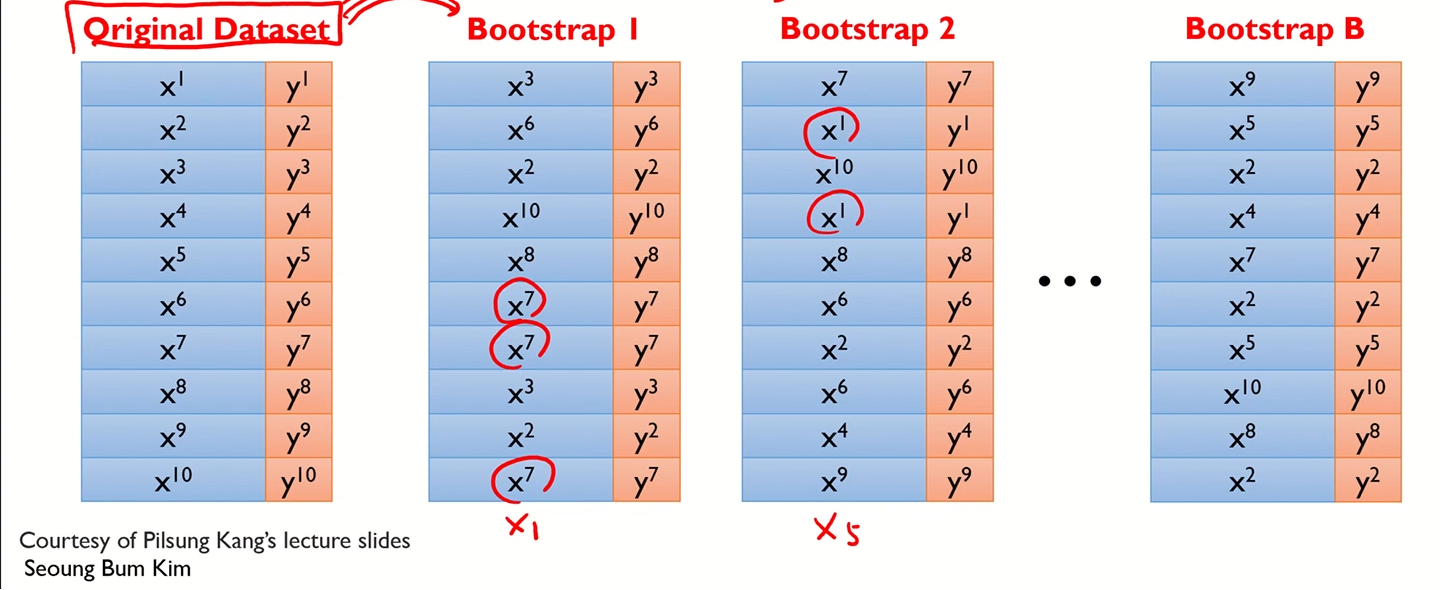
이론적으로 한 개체가 하나의 붓스트랩에 한 번도 선택되지 않을 확률

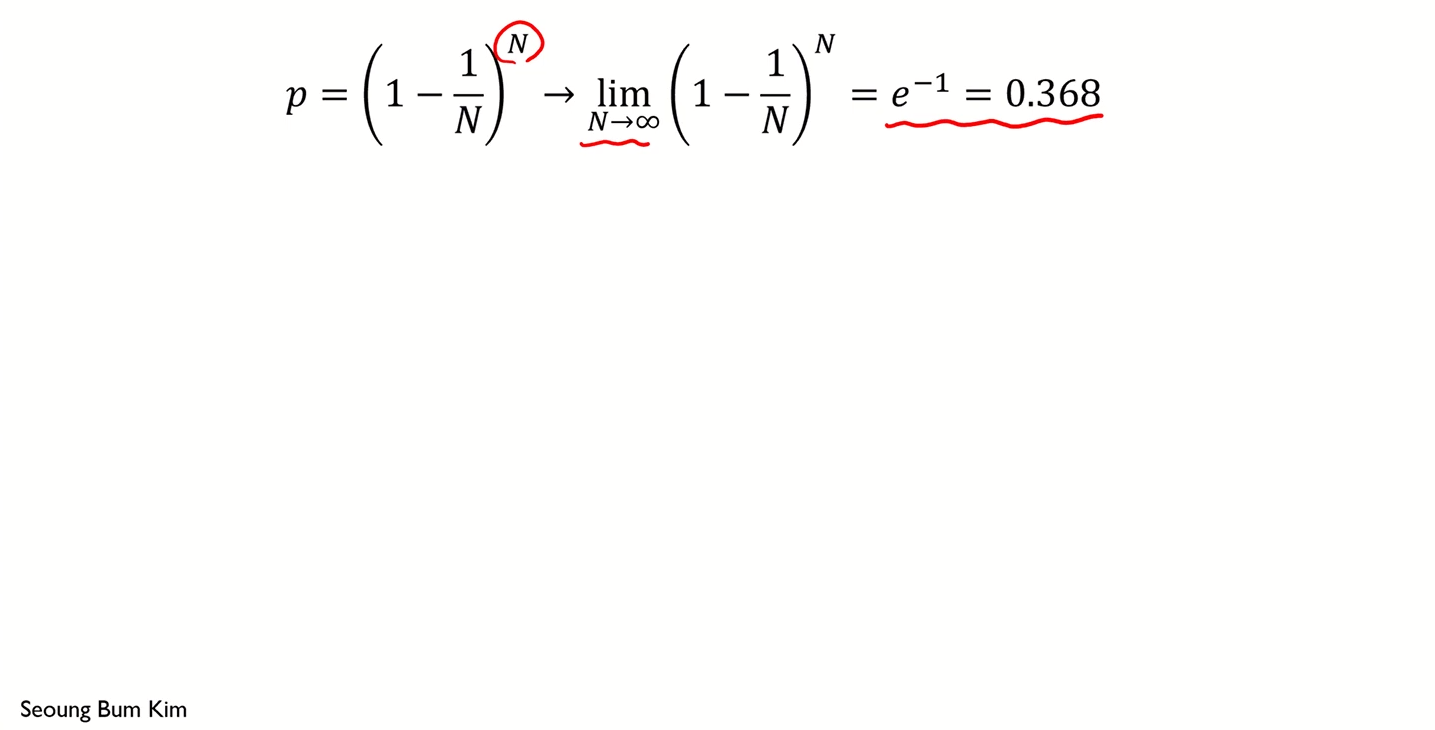
값이 꽤 큰 것을 알 수 있다.

---

Bagging (Bootstrap Aggregating)

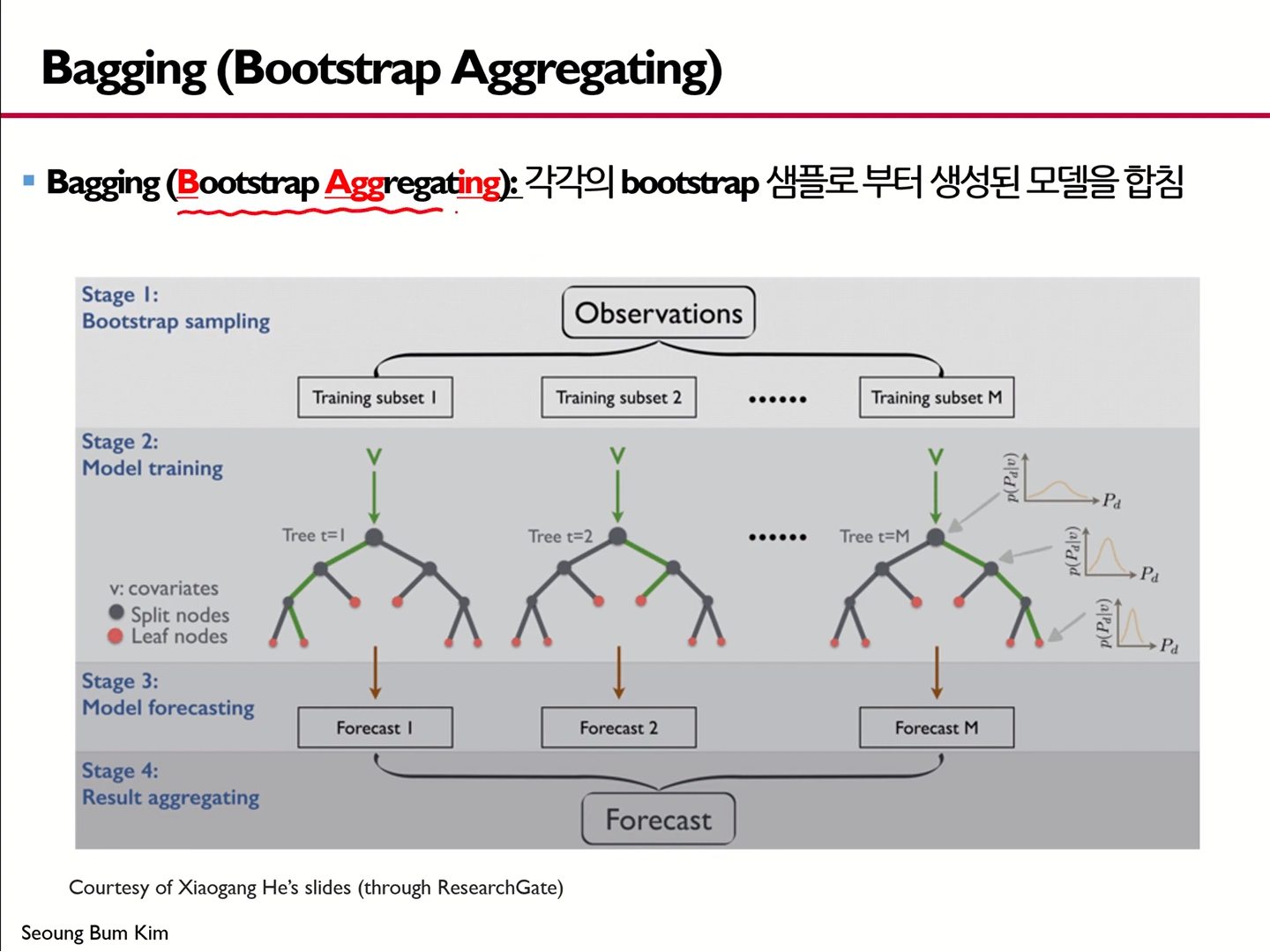
• 각각의 bootstrap 샘플로부터 생성된 모델을 합치는 것
  • 이 예시의 경우, 10개의 모델을 사용한 경우에 해당한다.

Classification task에서 Result Aggregating 방안 1

Classification task에서 Result Aggregating 방안 2

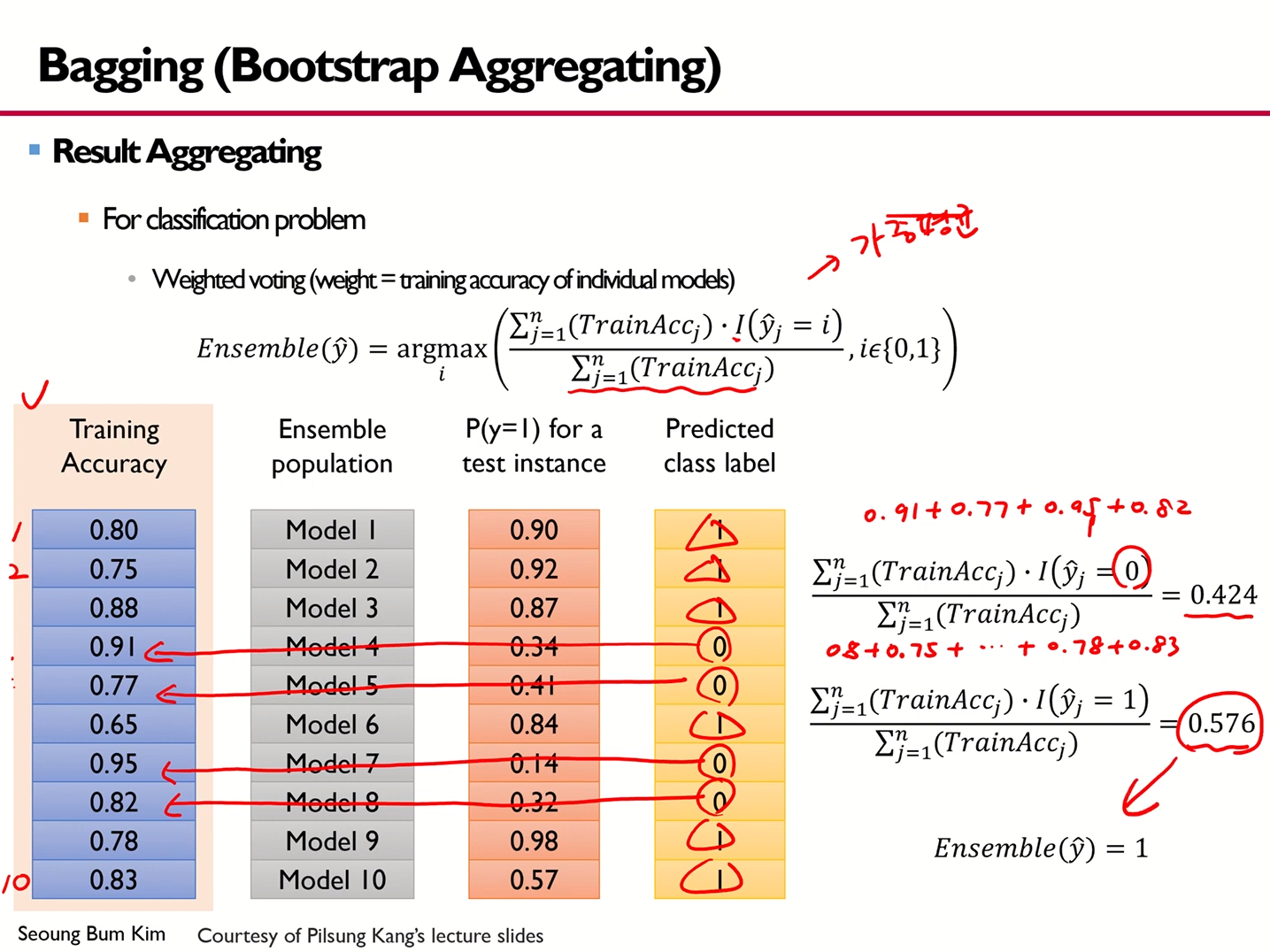
• 여기서 I 함수의 경우, Indicator함수에 해당한다.

Classification task에서 Result Aggregating 방안 3

Bagging Algorithm

---

Random Subspace

• Decision Tree에서는 분할기준과 분할점을 결정할 때 모든 가능성에 대해 확인한 뒤 최소의 cost function값을 갖는 경우를 채택했다.

그러나, Random Forest에서는 다르게 트리를 구축하게 된다.

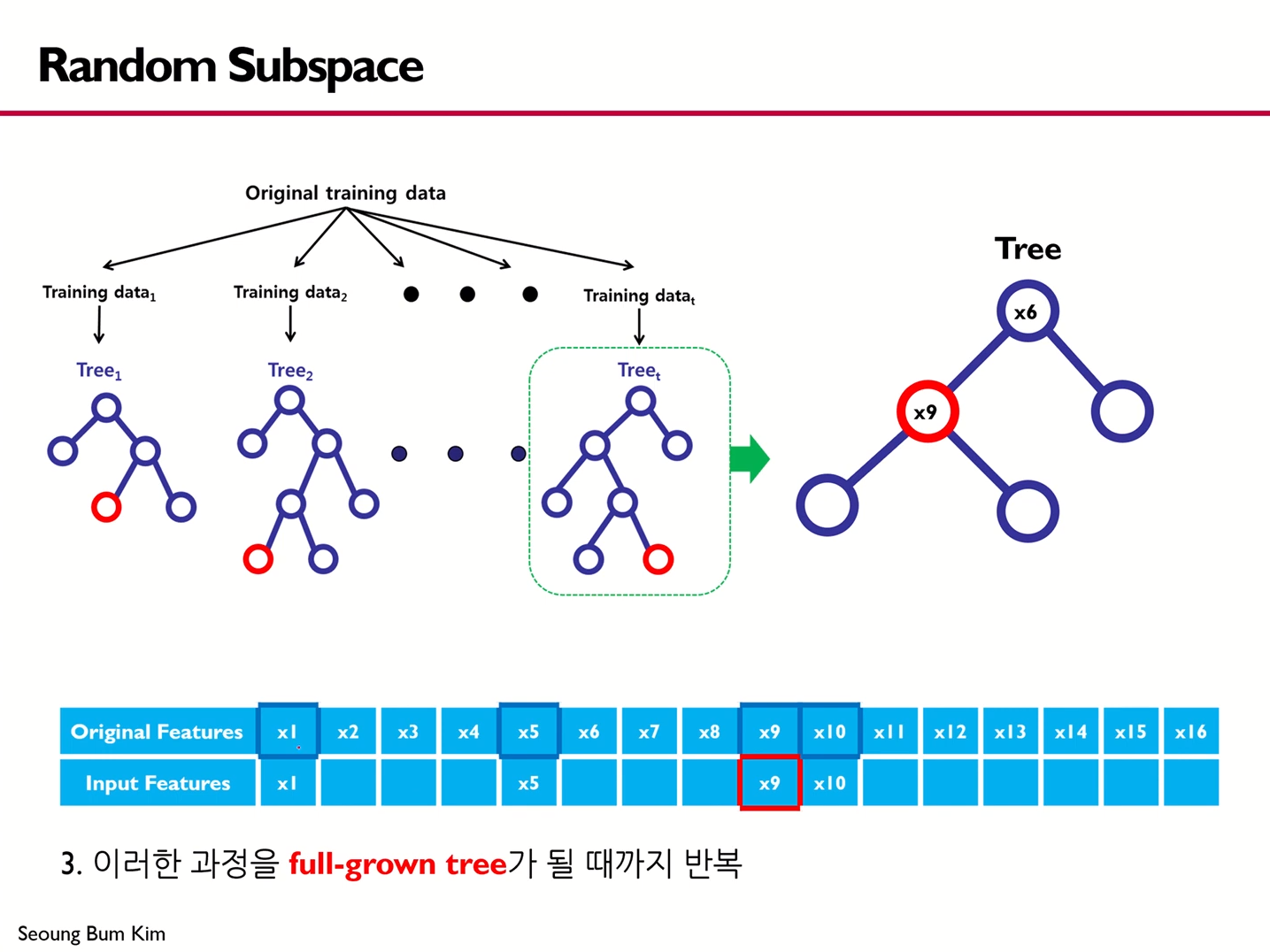
• 1. 원래 변수들 중에서 모델 구축에 쓰일 입력 변수를 무작위로 선택한다.
• 2. 선택된 입력 변수 중 분할될 변수를 선택한다.
• 이러한 과정을 full-grown tree가 될 때까지 반복해준다.
  

• 즉, Random Subspace방법의 경우, 의사결정나무의 분기점을 탐색할 때 원래 변수의 수보다 적은 수의 변수를 임의로 선택해 해당 변수들만을 고려 대상으로 한다.
  

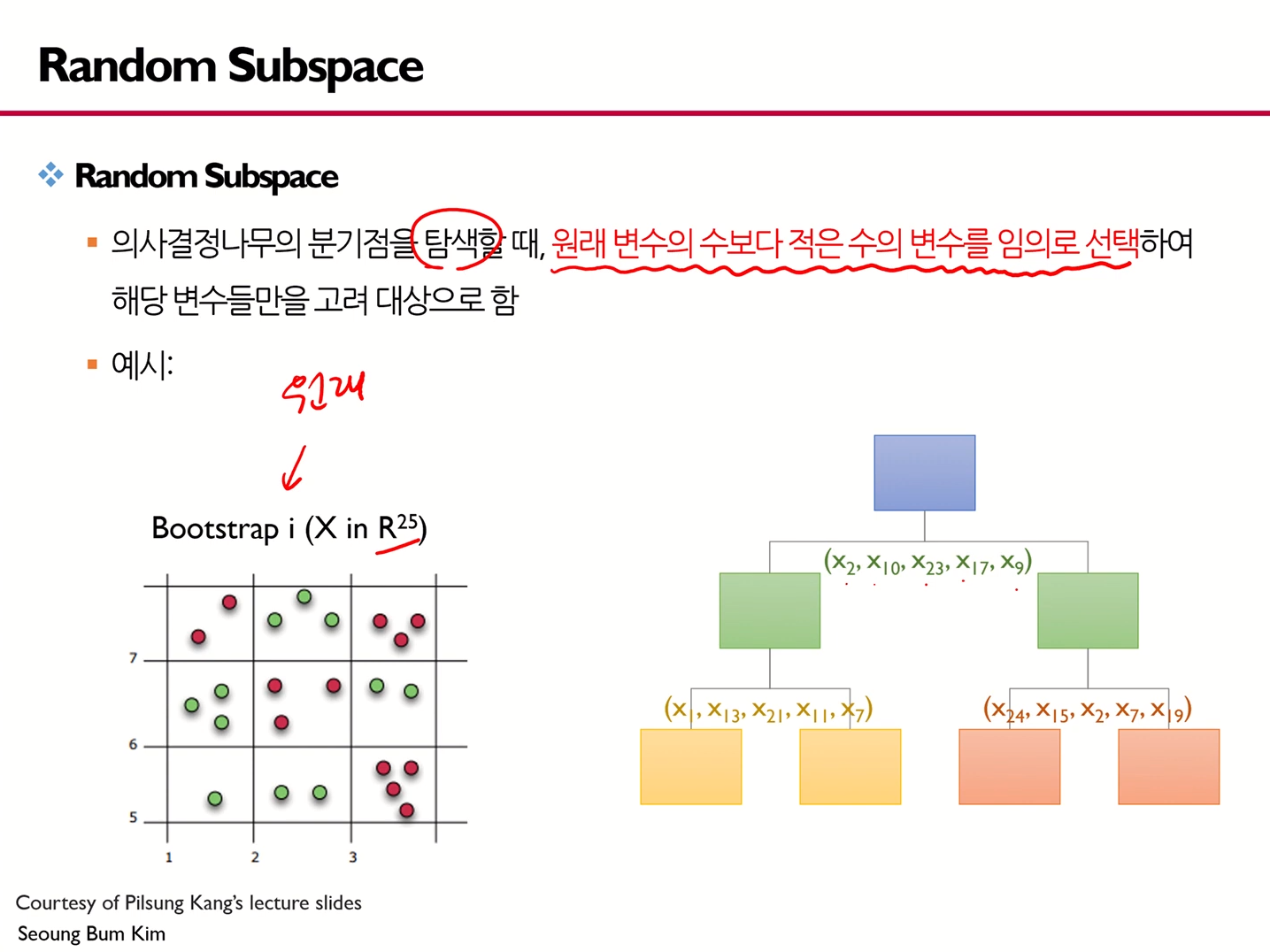
요런 느낌

---

Random Forest Model - Generalization Error

• 각각의 개별 tree는 과적합될 수 있다.
• Random forest는 tree 수가 충분히 많을 때 Strong Law of Large Numbers에 의해 과적합되지 않고, 그 에러는 limiting value에 수렴된다.

• 즉, Decision tree 간 상관관계 혹은 제대로 예측한 tree와 잘못 예측한 tree 수 차이의 평균을 키우던지 해야 함

---

Random Forest Model - 중요변수선택

• 변수의 중요도

  • 랜덤 포레스트 모델은 선형 회귀/로지스틱 회귀모델과는 달리 개별 변수가 통계적으로 얼마나 유의한지에 대한 정보를 제공하지 않음

    • 의사결정나무는 알려진 확률분포를 가정하지 않기 때문 (비모수적 모델)

  • 그러나, 랜덤 포레스트는 다음과 같은 간접적 방식으로 변수의 중요도 결정

    • 1. 원래 데이터 집합에 대해 Out of bag(OOB) Error를 구함
    • 2. 특정 변수의 값을 임의로 뒤섞은 데이터 집합에 대해 OOB Error를 구함
    • 3. 개별 변수의 중요도는 1단계와 2단계 OOB Error 차이의 평균과 분산을 고려해 결정됨

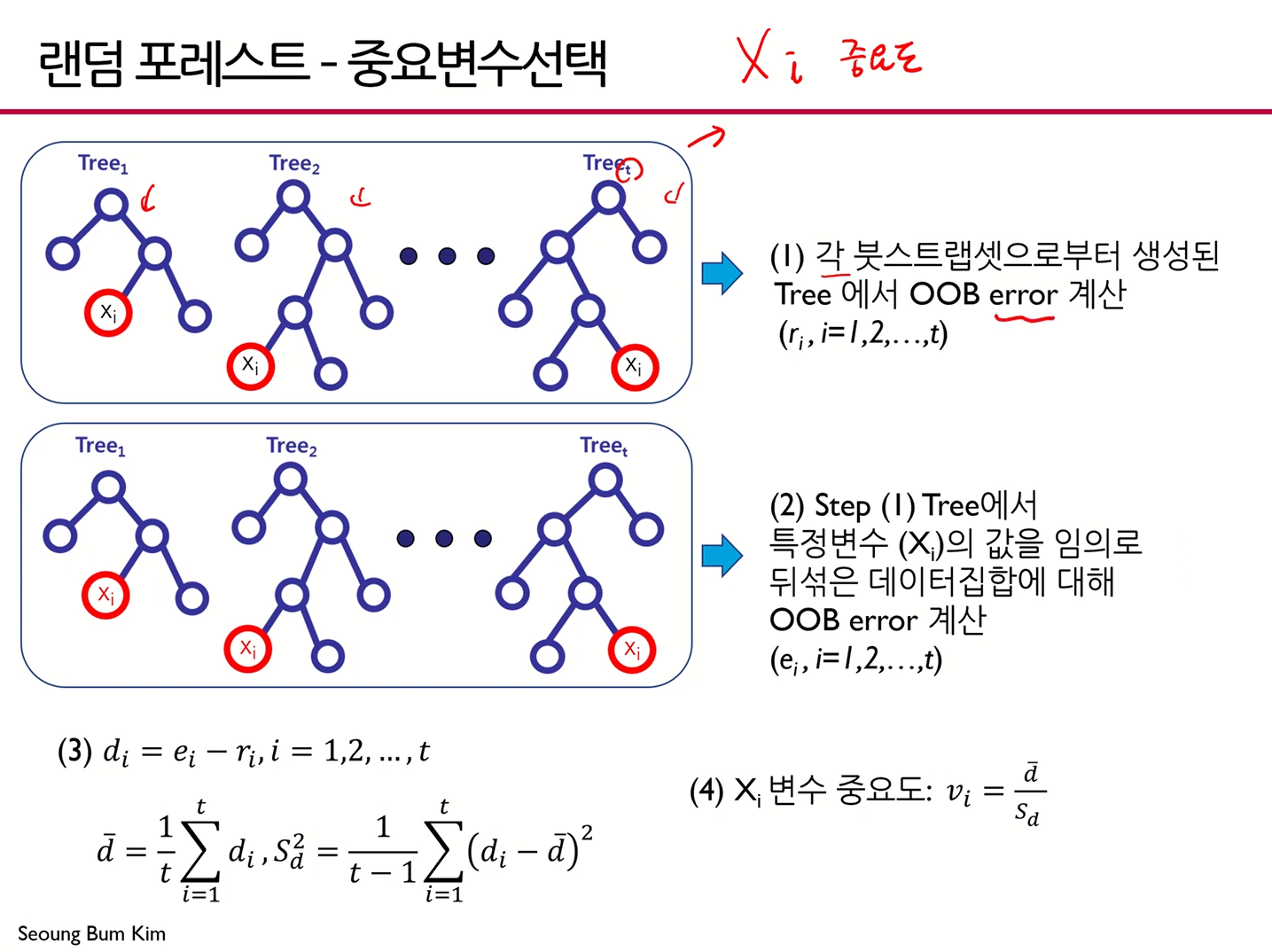
• (1)번 과정에서 OOB error란, Out of bag 데이터로부터 Error를 계산한 값에 해당
• (2)번 과정에서 특정 변수값을 임의값으로 바꿔준 후 OOB Error를 계산
  • 일반적으로, (2)번 과정으로부터의 OOB가 더 크게 나옴
• 위 식에서 $d_i$에 대해 절대값 씌워주면 좋을듯
  • $d_i$가 크다는 것은 해당 변수가 다른 변수로 대체됐을 때 성능이 매우 안좋아진다는 것
    • 즉, 차이의 평균이 클 수록 중요한 변수라는 것
    • 결국 "차이의 평균"이 핵심
  • 그 차이의 평균과 분산을 구해 $X_i$ 변수의 중요도를 구해준다.

---

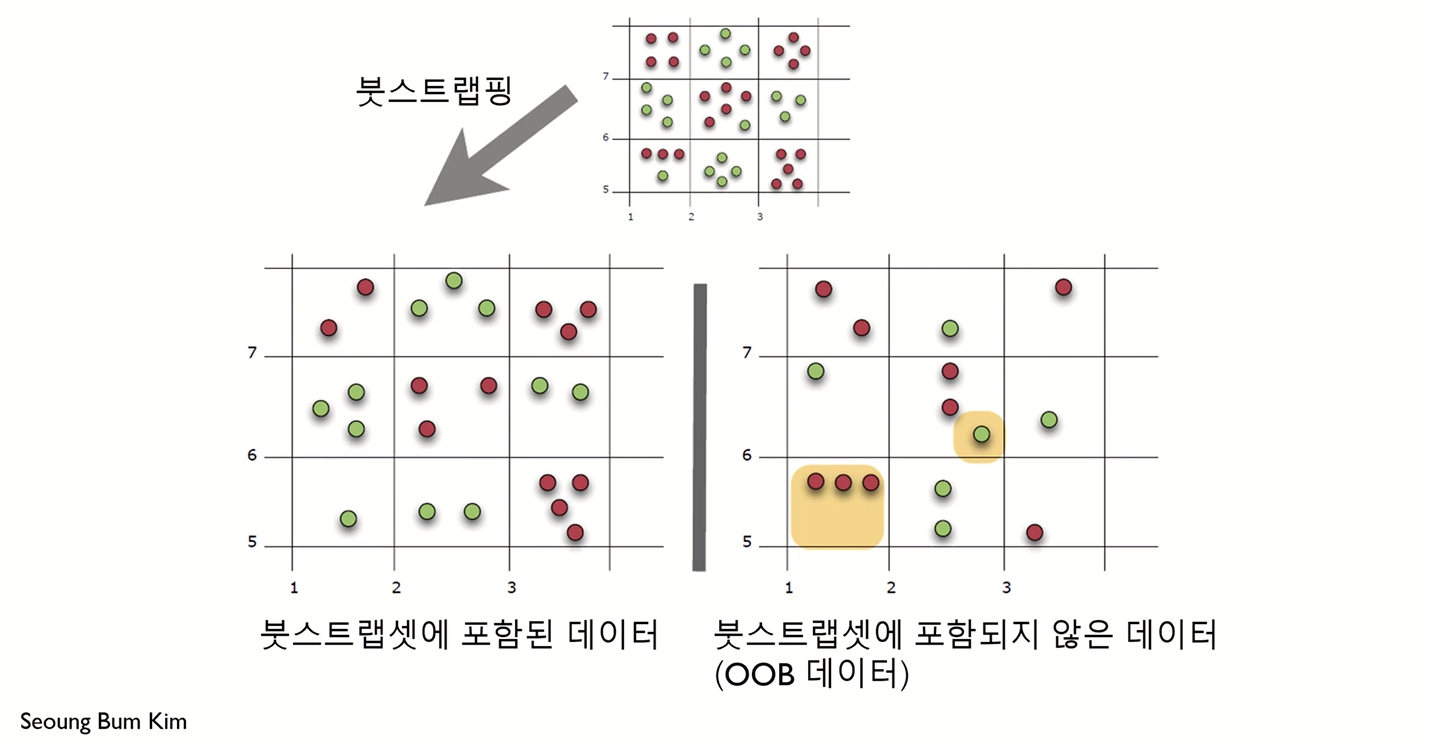
Out of bag(OOB)

• Bagging을 사용할 경우, Bootstrap set에 포함되지 않는 데이터들을 검증 집합으로 사용

---

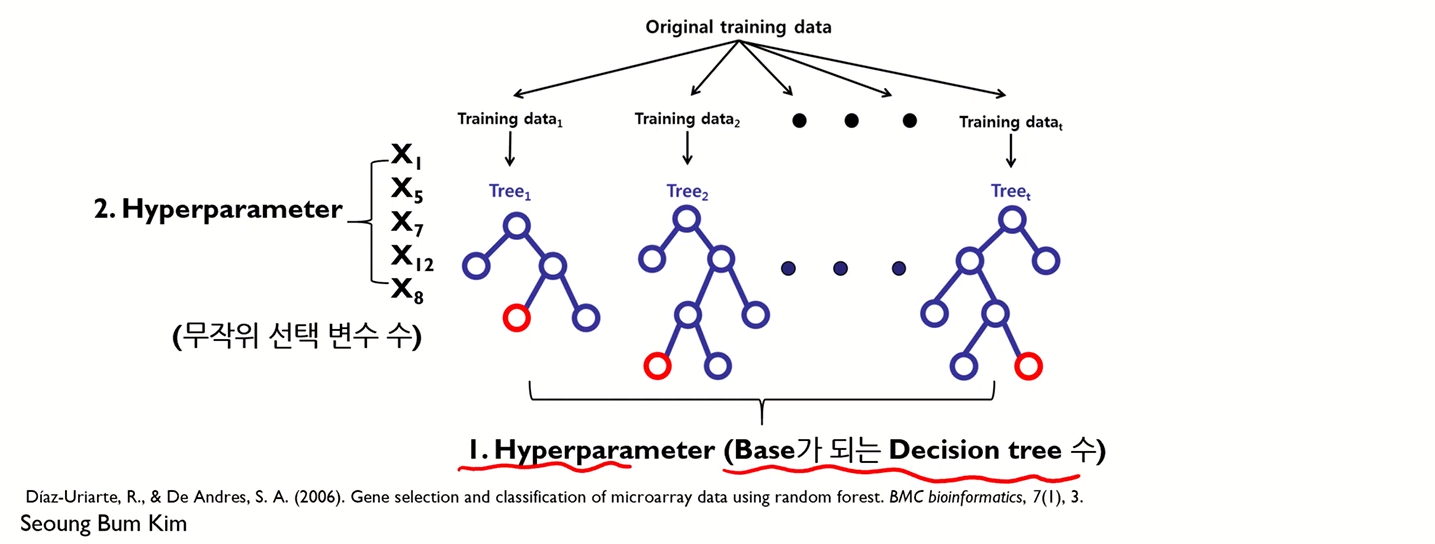
Random Forest Model - Hyperparameter

Decision Tree의 수

• Strong law of large numbers를 만족시키기 위해서는 2000개 이상의 decision tree가 필요

Decision tree에서 노드 분할 시 무작위로 선택되는 변수의 수

• 일반적으로 변수의 수에 따라 다음과 같이 추천됨
  • Classification: $\sqrt{변수의 수}$
  • Regression: 변수의 수 / 3

---

Random Forest Model - Algorithm