[MIT Deep Learning]CH9. Convolutional Networks

전민진·2022년 1월 25일

Deep Learning

목록 보기

2/4

9 Convolution Networks

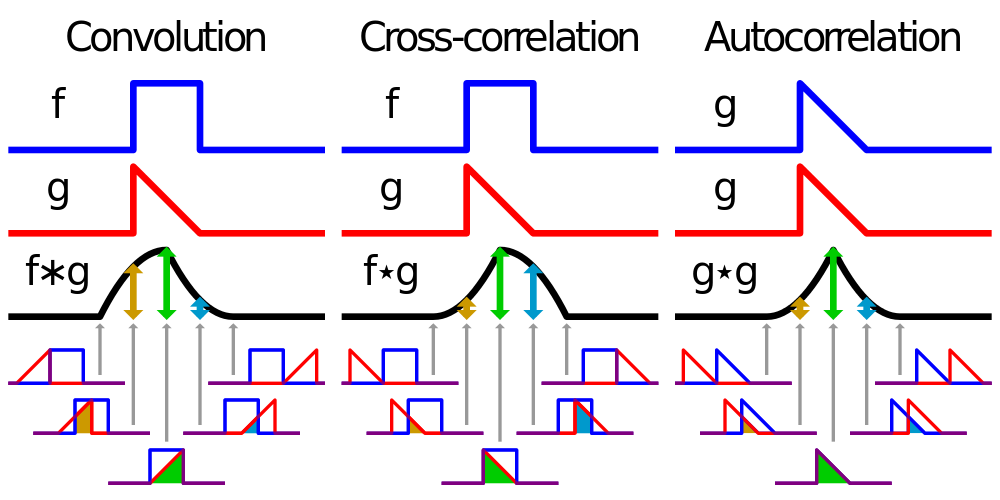
합성곱 : 두 함수를 곱해서 더함.

어떻게 두 함수를 곱해서 더할까? $(f*g)(t) = \int^{\infty}_{-\infty}f(\tau)g(x-\tau)d\tau$ 1 . 우선 합성곱을 위해선 두 함수 중 하나를 반전
2. 반전시킨 함수를 전이(shift)
3. 마지막으로 이동시킨 함수 g를 함수 f와 곱한 결과 기록
(이 때, 변수 $\tau$ 를 변화시키며 기록, 겹치는게 없으면 0이 되기도 함)

- 왜 쓸까?
: 주어진 입력값(신호, 행렬, 이미지..등)을 원하는 함수로 만들어 낼 수 있기 때문!(분해, 변환, 필터링 . . )
CNN에선 필터를 이용해 이미지의 특징(수평선, 수직선, 질감 표현, 패턴 등)을 포착!

9.1 The Convolution Operation

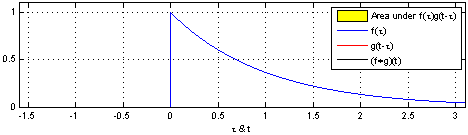
일반적으로, 합성곱은 실숫값을 받는 두 함수에 관한 연산이다.

예를 들어, 레이저 감지기를 이용해서 우주선의 위치를 추적한다. 레이저 감지기는 시간 $t$ 에서의 우주선의 위치를 뜻하는 $x(t)$ 를 출력한다. $x$ 와 $t$ 는 모두 실수이다. 즉, 시간 상의 임의의 순간에서 레이저 감지기는 매번 다른 값을 출력할 수 있다.
하지만, 이 레이저는 종종 출력에 잡음이 섞인다. 잡음을 줄이기 위해, 여러 추정값의 평균을 위치 추정값으로 사용하려고 한다. 여기에 더해, 최근의 측정값이 더 의미가 있으므로 최근의 값에 더 큰 가중치를 부여해 가중 평균을 구하려고 한다.

$a$ : 측정값의 나이
$w(a)$ : 가중치 부여하는 함수

s(t) = \int x(a)w(t-a)da = (x*w)(t)

$x$ : 입력값(input)
$w$ : 핵(kernel)
$s$ : 출력값, 특징맵이라고도 함

여기서, 레이저 감지기가 매 순간 측정값을 제공할 수 없으므로, 시간을 연속적인 값이 아니라 이산적인 값으로 취급하게 된다.

s(t) = (x*w)(t) = \sum^{\infty}_{a=-\infty}x(a)w(t-a)

일반적으로 머신러닝에서는

입력으로 다차원 배열(tensor)을, 핵으로 학습 알고리즘으로 적응(adaptive)되는 파라미터들의 다차원 배열(tensor)을 사용
무한합을 유한한 개수의 원소들로 이루어진 배열에 관한 합으로 구현
합성곱을 여러 축에 적용

2차원 이미지 $I$ 를 입력으로 사용할 때는 다음과 같이 2차원 핵 $K$ 를 사용한다.
$S(i,j) = (I *K)(i,j) = \sum_{m}\sum_{n}I(m,n)K(i-m,j-n)$
여기서 합성곱은 교환법칙을 만족하므로 다음과 같이 쓸 수 있다.
$S(i,j) = (I *K)(i,j) = \sum_{m}\sum_{n}I(i-m,j-n)K(m,n)$
핵을 뒤집는 대신 교차상관(cross-correlation)을 사용한다. $S(i,j) = (I *K)(i,j) = \sum_{m}\sum_{n}I(i+m,j+n)K(m,n)$

이산 합성곱

일부 성분들이 다른 성분들과 같아야 한다

단변량 이산 합성곱에서 행렬의 각 행은 반드시 그 위 행의 성부들을 한 자리 이동한 것과 같고, 이를 만족하는 행렬을 퇴플리츠 행렬(Toeplitz matrix)라고 한다.

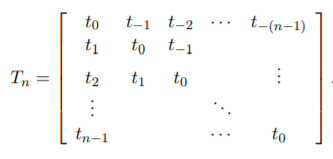
2차원의 경우, 이중 블록 순환 행렬(doubly block circulant matrix)가 합성곱에 해당한다.
보통 아주 희소한 행렬에 해당
: 핵이 이미지보다 훨씬 작기 때문

9.2 Motivation

합성곱 신경망은 머신러닝 시스템을 개성하는데 도움이 되는 3가지 중요한 개념을 활용한다.

희소 상호작용(sparse interaction)
: 핵이 입력보다 작기 때문에 발생한 성질

예를 들어, 이미지 처리에서 입력 이미지는 수천 또는 수백만 개의 픽셀로 이뤄지지만, 윤곽선 같은 작고 의미 있는 특징들은 단 수십 또는 수백 개의 픽셀로만 이뤄진 핵으로 검출할 수 있다.
- 상대적으로 적은 수의 매개변수들만 저장
- 모형의 메모리 사용량이 줄고, 통계적 효율성이 높아짐.
- 연산의 수도 줄어 듦
  입력 유닛이 m개, 출력 유닛이 n갤고 할 때, 행렬 곱셈에서는 m*n개의 파라미터가 관여한다. => $O(mn)$
  하지만 출력의 연결 수를 최대 k개로 제한한다면, 희소 연결 접근 방식에 필요한 매개변수는 kn개이다 => $O(kn)$
  
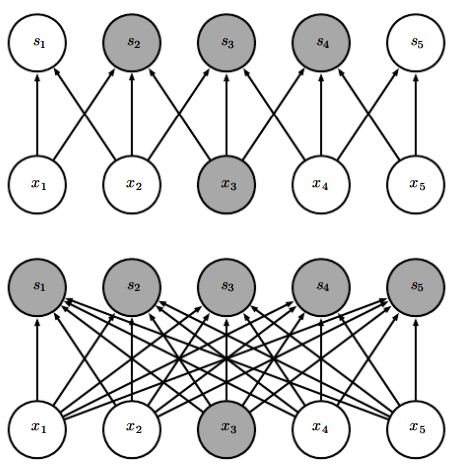
  위가 너비가 3인 핵으로 합성곱으로 할 때의 그림이고, 아래가 행렬 곱셈으로 출력을 산출할 때의 그림이다. 위에선 $x_{3}$ 이 영향을 끼치는 출력값이 3개지만, 모든 출력이 영향을 받는다.
  
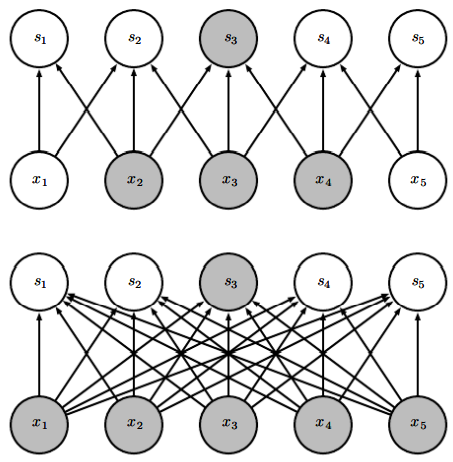
  희소 연결성을 위에서 본 모습이다. 출력 단위 하나와 그에 영향을 미치는 입력 단위를 강조하였다. 이러한 입력 단위들을 $S_{3}$ 의 수용 영역(receptive field)라고 한다.
- 합성곱 신경망에서 더 깊은 층들에 있는 단위들이 입력층의 더 큰 부분과 간접적으로 상호작용
  
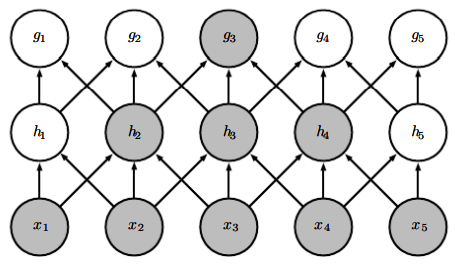
  층이 깊어질수록 유닛의 수용 영역은 더 얕은 층들에 있는 단위의 수용 영역보다 크다.(직접 연결은 드물지만 간접 연결은 대부분 된다!)
매개변수 공유(parameter sharing)
: 둘 이상의 함수에 같은 매개변수를 사용하는 것
합성곱 신경망에서 핵의 각 성분은 입력의 모든 곳에 쓰인다.
- 모형이 저장해야하는 매개변수 개수를 k로 줄인다
실행시간은 $O(kn)$ 이지만 $k$ 는 $m$ 보다 작고, mxn에 비하면 k는 사실상 무시할 정도로 작다.
=> 조밀한 행렬 곱셈보다 메모리 요구량과 통계적 효율성 면에서 뛰어나다.

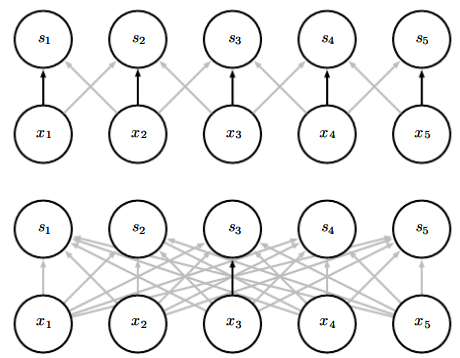
위에선 3성분 핵의 중앙 성분이 모든 입력 위치에서 쓰이지만, 아래에선 한 번만 쓰인다.

강아지 사진(320*280)에서 오른쪽과 같은 윤곽선을 검출한다고 할 때,
(2성분 핵을 가진)합성곱을 위한 FLOPS 319x280x3=약 26만회
행렬 곱셈을 위한 FLOPS 320x280x319x280 > 80억개
40억 배 더 효율적!
이동(translation)에 대한 등변성(equivariance)
어떤 함수가 등변이다 = 입력이 변하면 출력도 같은 방식으로 변함

$f(g(x)) = g(f(x))$ 이면 $f(x)$ 는 $g$ 에 대해 등변이다.

합성곱의 경우, 만일 $g$ 가 입력을 이동하는 함수이면, 합성곰 함수는 $g$ 에 대해 등변이다.

$I$ 가 정수 좌표에서 이미지의 밝기를 돌려주는 이미지 함수, g는 한 이미지 함수를 다른 이미지 함수로 사상하는 함수이되, $I'=g(I)$ 가 $I'(x,y)=I(x-1,y)$ 를 만족한다고 하자. 즉, $g$ 는 $I$ 에 해당하는 이미지의 모든 픽셀을 이동하는 효과를 낸다. 이 때, $I$ 에 이러한 변환 $g$ 를 적용한 후 합성곱을 적용한 결과는 $I'$ 에 합성곱을 적용한 후 변환 $g$ 를 적용한 결과와 같다.

이러한 성질은 적은 수의 인접 픽셀들을 처리하는 어떤 함수를 입력의 여러 위치에 적용하는 것이 바람직함을 알고 있을 때 유용

9.3 Pooling

일반적으로 합성곱 신경망의 한 층은 3단계로 작동한다.

다수의 합성곱을 병렬로 수행해 선형 활성화 값 산출

각 선형 활성화 값이 비선형 활성화 함수를 거침

풀링 함수를 이용해 그 층의 출력을 좀 더 수정

풀링 함수는 특정 위치에서 신경망의 출력을 근처 출력의 요약 통계량으로 대체

예를 들어, 최댓값 풀링(max pooling) 연산은 직사각형 영역 안에 있는 이웃 유닛 중 가장 큰 값을 사용.
이 외에도, 평균이나 L2 norm, 가중 평균 등의 풀링을 사용

어떤 경우든 풀링은 feature가 입력의 작은 이동에 대해 근사적으로 불변(invariant)이 되도록 한다.

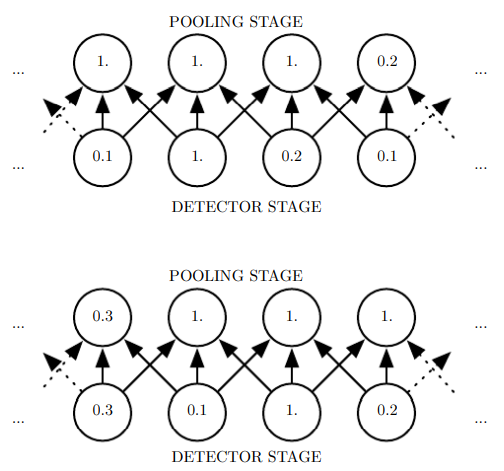
이동에 대한 불변성(invariance)
: 입력을 조금 이동해도 풀링된 출력들의 값이 대부분 변하지 않는 것

위의 그림에서 detector stage의 유닛의 값은 모두 한 칸씩 밀려서 값이 다 바뀌었지만, pooling stage의 값은 절반만 바뀐 것을 볼 수 있다.

어떤 feature의 구체적인 위치가 아니라 그런 특징의 존재 여부 자체가 더 중요할 땐, 이러한 국소 이동에 대한 불변성이 유용하다.

즉, 풀링을 적용한다는 것은 신경망의 층이 학습하는 함수가 작은 이동들에 대해 반드시 불변이어야 한다는 믿음을 나타내는 무한히 강한 사전분포를 신경망에 추가하는 것.

풀링은 이웃한 모든 단위의 반응을 요약하므로, 간격이 픽셀 하나가 아니라 픽셀 k개(stride = k)인 풀링 영역들의 요약통계량 보고하게 한다면 검출기 유닛보다 더 적은 수의 풀링 유닛을 사용해도 된다.
=> 다음 층이 처리해야 할 입력의 수가 약 k분의 1로 줄기 때문에 신경망의 계산 효율성이 좋아진다 + 통계적 효율성 증대, 메모리 요구량 감소

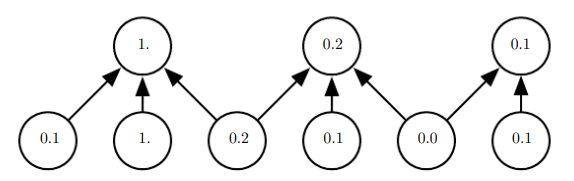
이 외에도 다양하게 풀링을 사용할 수 있다.

여러 특징을 동적으로 함께 풀링
: 흥미로운 특징들의 위치들에 대해 어떤 군집화 알고리즘을 실행해 풀링을 적용. 풀링 영역들이 이미지마다 다르게 형성
하나의 풀링 구조를 학습한 후 모든 이미지에 적용

9.4 Convolution and Pooling as an Infinitiely Strong Prior

사전확률분포

모형의 매개변수들에 관한 하나의 확률분포
바람직한 모형에 대한 우리의 사전 믿음(prior belief), 자료를 관측하기 전 우리가 가지고 있던 주어진 과제에 바람직한 모형이 어떤 것인가에 관한 우리의 믿음을 확률분포 형태로 부호화
사전분포의 확률밀도가 얼마나 조밀한지에 따라 "강하다" or "약하다"라고 표현
- 약한 사전분포는 엔트로피가 높은 사전분포
ex) 분산이 큰 가우스 분포
- 강한 사전 분포는 엔트로피가 아주 낮은 사전 분포
ex) 분산이 작은 가우스 분포
- 무한히 강한 사전 분포
  : 일부 매개변수 값들에 확률 0을 부여함으로써 그런 매개변수 값들이 절대로 허용되지 않음을 표현

합성곱을 사용하는 것은 한 층의 매개변수들에 관한 하나의 무한히 강한 사전분포를 도입하는 것과 같음.

무한히 강한 사전 분포는 한 은닛 유닛에 대한 가중치들이 그 이웃의 가중치들을 공간상에서 한 자리 이동한 것과 같아야 함을 뜻함.
또한, 은닛 유닛에 배정된, 작고 공간적으로 연속적인 수용 영역 이외의 곳에서는 가중치가 0이어야 함.
그 층이 배워야 하는 함수에 오직 국소적인 상호작용만 존재, 그 함수가 이동에 대해 등변이어야 함.

합성곱과 풀링이 과소적합(under fitting)을 일으킬 수 있음

합성곱과 풀링은 그 사전분포의 가정이 실제로 어느 정도 성립할 때만 유용
예를 들어, 정확한 공간 정보를 유지하는 것이 중요한 과제에선 모든 feature에 풀링을 적용하면 훈련 오차가 증가할 수 있음
그래서 일부 채널에만 풀링을 사용하는 것들도 있음
또한, 입력 공간 안에서 아주 멀리 떨어진 곳에 있는 정보를 가져와야 하는 과제에는 합성곱이 뜻하는 사전분포가 적절하지 않을 수 있음.

통계적인 학습 성과에 관한 벤치마트에서 합성곱 모형은 다른 합성곱들하고만 비교해야 함

합성곱을 사용하지 않은 모형은 이미지의 모든 픽셀을 치환(permutation)한다 해도 학습에 성공한다. ❓

9.5 Variants of the Basic Convolution Function

신경망에서 쓰이는 합성곱과 수학에서 말하는 이산 합성곱 연산이 정확히 일치하진 않는다!

신경망에서의 합성곱은 여러 합성곱을 병렬로 적용하는 하나의 연산이다.

하나의 핵을 가진 합성곱은 오직 한 종류의 특징만 추출
하지만 신경망에선 각 층이 여러 위치에서 여러 가지 특징을 추출하는 것이 바람직

신경망에서의 합성곱은 입력이 그냥 실숫값들의 격자가 아니라, 각각 여러 개의 관측값들로 이루어진 벡터들의 격자이다.

원색 이미지의 경우 R, G, B 3가지의 색의 세기로 색상을 표현
=> 보통 이미지는 3차원 텐서로 간주
또한, 구현 시 흔히 배치 모드로 작동하기 떄문에, 특정 배치를 지정하는 4번째 차원이 추가된 4차원 텐서를 사용할 때가 많음.

합성곱 신경망은 흔히 다채널 합성곱을 사용하는데, 이러한 합성곱이 기초하는 선형 연산들이 반드시 가환적이지 않다.

각 연산의 출력 채널 수와 입력 채널 수가 같을 때만 교환 법칙을 만족

합성곱 신경망의 다양한 버전

기본 버전
- 출력의 $i$ 번째 채널의 한 단위와 입력의 $j$ 번째 채널의 한 단위의 연결 강도(세기)에 해당하는 성분 $K_{i,j,k,l}$ 들로 이루어진 4차원 핵 텐서 $K$ 가 있다고 하자.
- 각 성분에서 k와 l은 해당 유닛의 행 번호와 열번호 이다.
- 입력으로 쓰이는 데이터 $V$ 는 채널 i의 j행 k열의 관측값을 담은 성분 $V_{i,j,k}$ 로 이뤄지고, 출력에 해당하는 텐서 $Z$ 도 같은 구조이다.
- $K$ 를 뒤집지 않고 $K$ 와 입력 $V$ 의 합성곱으로 출력 $Z$ 를 산출한다면, 출력의 각 성분은 다음과 같이 주어진다.

$Z_{i,j,k} = \sum_{l,m,n} V_{l, j+m-1, k+n-1}K_{i,l,m,n}$
```
우변의 합의 범위는 유효한 입력 성분과 핵 성분을 가리키는 텐서 인덱스 l,m,n의 모든 값이다.
```
stride가 있는 합성곱
: 계산 비용을 줄이기 위해 핵의 일부 위치를 건너 뛸 수 있다.
(대신 특징을 세밀하게 추출하진 못함)
: 다음은 출력의 각 방향에서 픽셀 s개바다 한 번씩만 출력을 산출하는 하향표본화된 합성곱 함수 c의 정의이다.
$Z_{i,j,k} = c(K,V,s)_{i,j,k}= \sum_{l,m,n}[ V_{l, (j-1)*s+m, (k-1)*s+n}K_{i,l,m,n}]$
- 이 공식에서 s를 하향 표준화의 보폭(stride)라 부른다.
입력 $V$ 에 0 채우기를 아예 사용하지 않는 경우(valid conv)
- 핵 전체가 이미지 안에 완전히 들어가는 위치들만 방문할 수 있다.
- 출력의 크기가 각 층에서 줄어든다
  : 입력 이미지의 너비가 m이고 핵의 너비가 k이면 출력의 너비는 m-k+1이 된다.
출력과 입력이 같은 크기가 될 정도로만 0들을 채우는 것(same conv)
- 합성곱 연산이 다음 층에 대한 구조적 가능성을 축소하지 않음
- 가장자리 부근의 입력 픽셀들은 중앙 부근의 입력 픽셀들보다 적은 수의 출력 픽셀들에 영향을 끼침.
각 방향에서 모든 픽셀이 k번 방문되도록 충분히 많은 0을 채움(full conv)
- 이 경우 출력 이미지의 너비는 m+k-1이 된다.
- 가장자리 부근의 픽셀이 중앙 부근의 출력 픽셍보다 더 적은 수의 입력 픽셀들에 영향을 받음
- 합성곱 특징 맵의 모든 위치에서 잘 작동하는 하나의 핵을 학습하기가 어려울 수 있음
  ==> 보통의 경우 최적의 0 채우기 분량은 valid와 same 합성곱 사이의 한 지점이다.
합성곱 대신 층들을 국소적으로 연결하는 것 (= 비공유 합성곱, unshared convolution)
- 합성곱 신경망과 동일할 것 같지만 모든 연결에 각각 고유한 가중치가 부여됨.
합성곱과 비슷하되 여러 위치에서 매개변수들을 공유하지 않음.
$Z_{i,j,k} = \sum_{l,m,n} V_{l, j+m-1, k+n-1}K_{i,j,k,l,m,n}$
==> 국소적으로 연결된 층들은 각 특징이 반드시 공간의 작은 부분의 함수이고, 그 특징이 공간의 모든 곳에 나타난다고 생각할 이유가 없는 경우에 유용

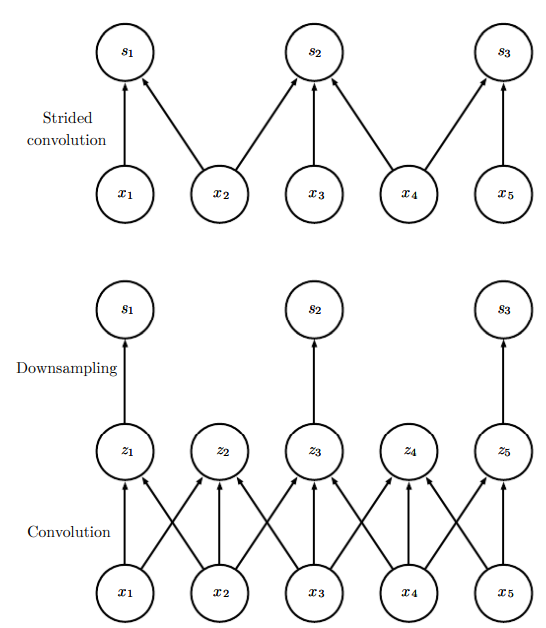
위가 패치의 크기가 2픽셀인 국소 연결층, 가운데가 핵의 너비가 2픽셀인 합성곱 층, 마지막이 완전 연결 층.
위와 가운데의 차이는 위에선 모든 간선의 가중치가 서로 다름. 하지만 가운데는 같은 파라미터를 거듭해서 사용
합성곱이나 국소 연결 층들의 연결성을 좀 더 제한한 특별한 버전을 만드는 것이 유용
- 예를 들어, 각 출력 채널 i가 오직 입력 채널 l의 한 부분집합의 함수이어야 한다는 제약
- 처음 m개의 출력 채널을 처음 n개의 입력 채널들에만 연결하고, 다음 m개의 출력 채널들은 그다음 n개의 입력 채널들에만 연결
  ==> 신경망의 매개변수 개수 줄임.(메모리 소비량 감소, 통계적 효율성 증가, 학습 계산량 감소)
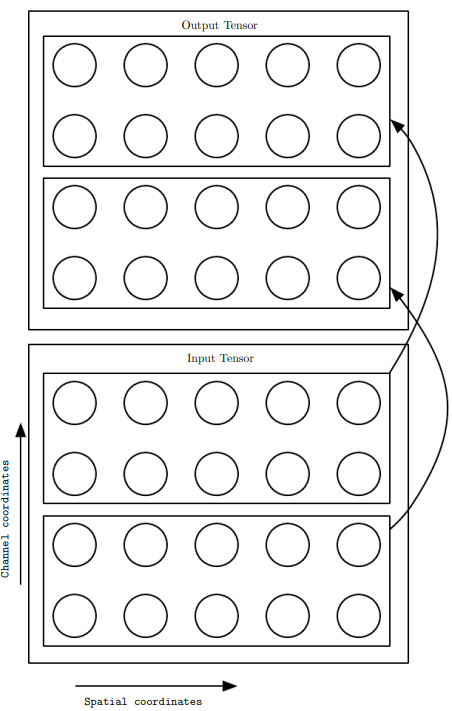
타일식 합성곱(tiled convolution) ❓
- 합성곱 층과 국소 연결 층 사이의 한 절충에 해당
- 모든 위치에서 개별적인 가중치 집합을 학습하는 대신, 공간을 나아가는 과정에서 순환되는핵들의 집합을 학습 ❓
- 국소 연결 층에서처럼 인접한 이웃 위치들에 각자 다른 필터들이 적용되지만, 파라미터를 저장하는데 필요한 메모리 요구량은 그러한 핵 집합의 크기에만 비례해서 증가
- 핵들을 쌓아서 만든 6차원 텐서 $K$ 가 쓰이고, 이 텐서의 2개의 차원은 출력맵의 한 위치를 결정한다.
- 나머지 4개의 차원이 각 방향에서 t가지 서로 다른 핵 중 하나가 출력 위치에 따라 순환적으로 선택된다.
- 만약 t(타일링 범위)가 출력의 너비와 같으면 국소 연결층과 같은 구조가 된다. $Z_{i,j,k} = \sum_{l,m,n} V_{l,j+m-1,k+n-1}K_{i,l,m,n,j\%t+1,k\%t+1}$
- 여기서 퍼센트 기호는 나머지 연산을 뜻한다.
  
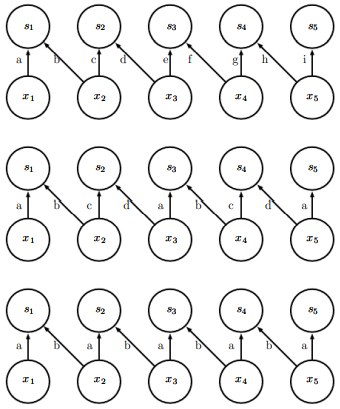
  순서대로 국소 연결층, 타일식 합성곱, 표준 합성곱이다.

임의의 깊이의 순방향 합성곱 신경망의 훈련에 필요한 모든 기울기를 계산하는 데에는 1)합성곱, 2)출력에서의 가중치로의 역전파, 그리고 3)출력에서 입력으로의 역전파라는 3가지 연산만 있으면 된다.

간격 있는 합성곱 연산을 다채널 이미지 $V$ 에 적용하는 합성곱 신경망을 훈련한다고 하자. 합성곱의 보폭이 $s$ 이고 핵들의 텐서가 $K$ 라고 할 때, 합성곱 연산은 $c(K,V,s)$ 로 정의된다. 어떤 손실함수 $J(V,K)$ 를 최소화한다고 하자.

순전파 과정에서는 $c$ 함수 자체가 $Z$ 출력

역전파 과정에서는 $G_{i,j,k} = \frac{\partial}{\partial Z_{i,j,k}}J(V,K)$ 를 만족하는 텐서 $G$ 받게 됨 $g(G,V,s)_{i,j,k,l} = \frac{\partial}{\partial V_{i,j,k,l}}J(V,K) = \sum_{m,n} G_{i,m,n}V_{j,(m-1)s+k, (n-1)s+l}$ 만일 현재 층이 신경망의 바닥(최하단)층이 아니라면, 오차를 더 아래 층으로 역전파하기 위해 $V$ 에 대한 기울기를 계산할 필요가 있다. $h(K,G,s)_{i,j,k} = \frac{\partial}{\partial V_{i,j,k}}J(V,K)= \sum_{l,m(단 (l-1)s+m=j)}\sum_{n,p (단, (n-1)s+p=k)} \sum_{q}{K_{q,i,m,p}G_{q,l,n}}$

CNN 역전파 관련 참고자료
https://ratsgo.github.io/deep%20learning/2017/04/05/CNNbackprop/

9.6 Structured Outputs

합성곱 신경망이 분류 과제에서 하나의 라벨을 예측하거나 회귀 과제에서 하나의 실숫값을 예측하는 대신, 어떤 고차원 구조적 객체(어떤 이미지의 픽셀이 부류 i에 속할 확률)을 출력하게 할 수 있다.

이 때 문제가 되는 부분이 출력 평면이 입력 평면보다 작을 수 있다는 것이다.

입력과 비슷한 크기의 출력 맵을 산출하는 방법에는
1) 풀링을 아예 사용하지 않는 것
2) 표지들의 저해상도 격자를 산출하는 것
(to simply emit a lower-resolution grid of labels)
3) 단위 보폭 풀링 연산자를 사용하는 것
(use a pooling operator with unit stride)
이 있다.

이미지의 픽셀별 라벨 부여를 위한 한 가지 전략은,
1) 먼저 이미지 라벨의 초기 추측을 만들고, 그 초기 추측들을 이웃 픽셀들과의 상호작용을 이용해 좀 더 정교하게 만듦
2) 이러한 단계를 여러 번 반복
=> 가중치를 공유하며 일련의 계산 수행하는 인접한 합성곱 층들은 특별한 종류의 순환 신경망에 해당 ❓
3) 각 픽셀의 라벨을 예측한 다음에 다양한 방법으로 예측을 정교화해서 입력 이미지를 여러 영역으로 나눌 수 있다.(segmentation)
=> 비슷한 값을 가진 다수의 인접한 픽셀들은 같은 표지에 속할 가능성이 크다!
=> 그래프 모형은 이웃 픽셀들 사이의 확률적 관계를 서술할 수 있다. 혹은 그래프 모형의 훈련 목적함수의 근삿값을 최소화하도록 합성곱 신경망을 훈련할 수도 있다.

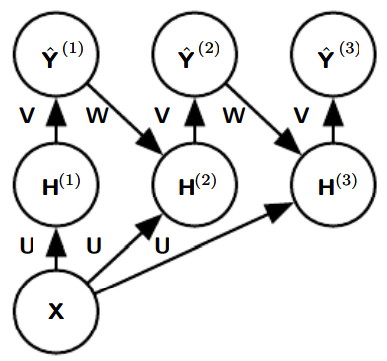
픽셀에 라벨을 부여하기 위한 순환 합성곱 신경망의 예. 입력은 이미지 텐서 $X$ 로, 텐서의 축들은 이미지의 행들과 열들, 그리고 채널들에 대응된다. 목표는 $\hat{Y}$ 를 산출하는 것인데, 이는 각 픽셀의 라벨에 관한 하나의 확률분포를 의미한다. 순환 신경망은 이러한 $\hat{Y}$ 를 단번에 출력하는 대신, $\hat{Y}$ 을 추정하고 그것을 입력으로 삼아 추정을 좀 더 정교하게 한다. 이를 원하는 만큼 반복할 수 있는데, 모든 반복에서 같은 파라미터를 사용한다.

9.7 Data Types

일반적으로, 합성곱 신경망에 쓰이는 데이터는 여러 채널로 구성된다. 이 채널들은 시간 또는 공간의 한 지점에서 서로 다르 어떤 양(quantity)를 관측한 값들이다.

지금까지는 학습 데이터셋과 테스트 데이터셋의 데이터가 모두 같은 차원(공간)인 경우만 생각했다. 하지만, 합성곱 신경망의 한 가지 장점은 공간적 차원이 서로 다른 입력도 처리할 수 있다는 것이다.

예를 들어, 너비와 높이가 서로 다른 이미지들은 처리한다고 할 때, 고정된 크기의 가중치 행렬로는 이러한 입력들은 어떻게 모델링할지 명확하지 않다. 하지만 합성곱 신경망을 적용하는 것은 간단하다. 핵(kernel)은 그냥 이미지의 크기의 맞는 횟수만큼 적용되며, 이에 따라 합성곱 연산의 출력의 크기도 적절히 결정된다.

혹은 신경망의 입력 뿐만 아니라 출력의 크기도 가변적이어야 할 때가 있는데, 이 경우 풀링을 도입하는 등의 추가적인 설계가 필요하다.

가변 크기 입력을 처리하기 위해 합성곱을 사용하는 것은

같은 종류의 대상을 측정한 값들의 양이 달라 입력의 크기가 다른 경우에만 유효하다(사진의 해상도가 다른 경우)
관측값의 종류 자체가 달라서 입력의 크기가 다른 경우엔 적합하지 않다!(특정 항목이 생략될 수 있는 경우)

9.8 Efficient Convolution Algorithms

합성곱 연산은 입력과 핵 모두를 푸리에 변환(Fouier transform)을 이용해 두 신호의 점별(point-wise)곱셈을 통해 주파수 정의역으로 변환하고, 역 푸리에 변환을 이용해 다시 시간 정의역으로 변환하는 것과 동등하다.
=> 문제에 따라선 이산 합성곱 연산을 그대로 구현하는 것보다 이러한 푸리에 변환을 구현해서 합성곱을 계산하는 것이 더 빠를 수 있다.

d차원 핵을 d개의 벡터들(차원당 벡터 하나씩)의 외적으로 표현할 수 있을 때, 이러한 핵을 가리켜 분리 가능(separable; 분해 가능)이라고 부른다. 핵이 분리 가능할 때는 보통 방식의 합성곱 계산은 효율적이지 않다. 이 경우 합성곱은 그러한 각 벡터와의 1차원 합성곱 d개를 결합한 것과 동등하다.

벡터들의 외적과의 d차원 합성곱 하는 것보다 빠름
핵이 벡터를 표현하는데 필요한 매개변수들도 적다
- 보통의 다차원 합성곱의 실행시간과 매개변수 저장공간 요구량 = $O(W^d)$ 이지만 분리 가능한 핵의 합성곱 실행 시간과 매개변수 저장 요구량은 $O(Wd)$ 이다.

9.9 Random or Unsupervised Features

일반적으로 합성곱 신경망 훈련에서 비용이 가장 많이 드는 부분이 feature의 학습이다(출력층은 풀링으로 크기가 축소되기 때문에 비용이 낮다). 경사 하강법으로 지도 학습을 할 때, 각각의 경사 하강 단계에선 신경망 전체를 훑는 완전한 순전파와 역전파를 각각 한 번씩 수행해야 한다.

이러한 학습 비용을 줄이는 방법은 지도 학습의 방식으로 학습되지 않은 feature들을 사용하는 것이다.

지도 학습을 요구하지 않는 합성곱 핵 얻기

핵들을 무작위로 초기화

잘될 떄가 은근 있다. 합성곱 다음에 풀링을 적용하는 층들에 무작위로 가중치를 부여하면 그 층들이 자연스럽게 주파수 선택적(frequence selective)이자 이동 불변적인 방식으로 작동한다.
핵들을 사람이 직접 설계

특정 방향 또는 특정 크기의 가장자리들을 검출하도록 설정
비지도 판정조건을 이용해 핵 학습

k-means clustering을 작은 이미지 패치들에 적용한 후, 학습된 각각의 무게중심을 하나의 합성곱 핵으로 사용.

=> 비지도 판정기준으로 학습하면 신경망 아키텍처 위에 놓인 분류층에서 그 특징들을 개별적으로 결정하는 것이 가능하다.