원래는 Regularized Linear Regression의 개념과 관련 알고리즘들(릿지회귀, 라쏘회귀, 엘라스틱 넷)에 대해서 공부를 하려고 했는데 그 전에 Bias-Variance trade-off에 대해 먼저 정리를 하고 Regularized Linear Regression에 대해서 공부를 하면 좋을 거 같아 글을 작성하게 되었다.
편향-분산 트레이드-오프(Bias-Variance trade-off)
편향-분산 트레이드-오프(Bias-Variance trade-off)에 대해 위키백과에서는 ‘지도 학습 알고리즘이 훈련 데이터의 범위를 넘어 지나치게 일반화 하는 것을 예방하기 위해 두 종류의 오차(편향 오차, 분산 오차)를 최소화 할 때 겪는 문제이다. ‘ 라고 되어있으나 이 한문장만 보고는 이해하기 어려운거 같다. 그래서 먼저 위키백과에서 이야기 하는 편향(Bias)과 분산(Variance)이 무엇인지 알아 보고 왜 이 둘이 trade-off관계인지 알아보려고 한다.
편향(Bias)과 분산(Variance)
편향(Bias)은 학습 알고리즘에서 잘못된 가정을 했을 때 발생하는 오차이다. 쉽게 말해서 실제로 데이터는 3차항의 관계를 가지고 있는데 모델을 1차항으로 가정하게 되면 예측치와 실제값의 차이가 커지게 되므로 편향값이 커지게 된다. 편향값이 커지게 되면 모델이 데이터를 잘 설명하지 못하는 상태이므로 과소적합(Underfitting)문제를 발생시킬 수 있다.
분산(Variance)은 훈련 데이터에 있는 작은 변동에 모델이 과도하게 민감하기 때문에 발생하는 오차이다. 만약 데이터가 약 10차항의 관계를 가지고 있다고 가정하자. 이때 모델이 지나치게 민감하다면 10차항의 관계를 가진 데이터를 설명하기 위해 모델 또한 매우 복잡해질 것이고 분산값이 매우 커질것이다. 자유도가 높은 모델은 높은 분산값을 가지기 쉬워 훈련데이터에 과대적합(Overfitting) 문제를 발생시킬 수 있다.
편향과 분산의 정의를 알았으니 ‘편향도 최소값을 가지고 분산도 최소값을 가지는 모델이 가장 좋은 모델이 아닌가?’ 라는 생각을 해볼 수 있다. 하지만 아쉽게도 편향도 작고 분산도 작은 모델은 존재할 수 없다. 왜 그럴 수 없는지, 둘의 관계가 왜 trade-off 관계인지 알아보자.
편향-분산 분해(Bias-Variance Decomposition)
편향-분산 분해(Bias-Variance Decomposition)은 정규화(Regularization)의 이론적인 배경으로 알려져 있으며 모델의 일반화 오차를 다른 세 가지 종류의 오차(편향, 분산, 줄일수 없는 오차)로 나눌 수 있다는 내용이다. 데이터들의 관계를 이라 정의 했을 때 MSE를 편향, 분산, 줄일 수 없는 오차를 사용해서 수식을 작성해보자.
위 식을 통해서 분산과 편향의 trade-off 관계를 확인할 수 있다. 내가 이해한것이 맞는지는 모르겠지만 위와같은 상황에서 만약 분산을 0으로 하기위해 =라고 설정하면하게 되면 x의 값에 따라 편향값이 매우 커질수도 있고, 반대로 편향값을 0으로 만들기 위해 =라고 설정하게 되면 분산값이 매우 커지게 되므로 trade-off 관계라고 볼 수 있다. 이를 그래프로 그린다면 다음과 같은 관계를 가지게 된다.
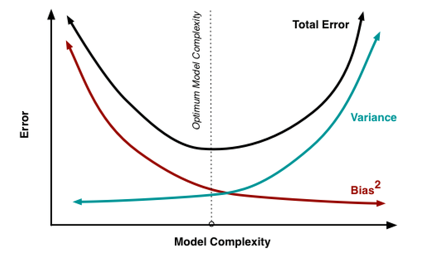
좀더 직관적으로 알아보기 위해 다음 그림을 보자.
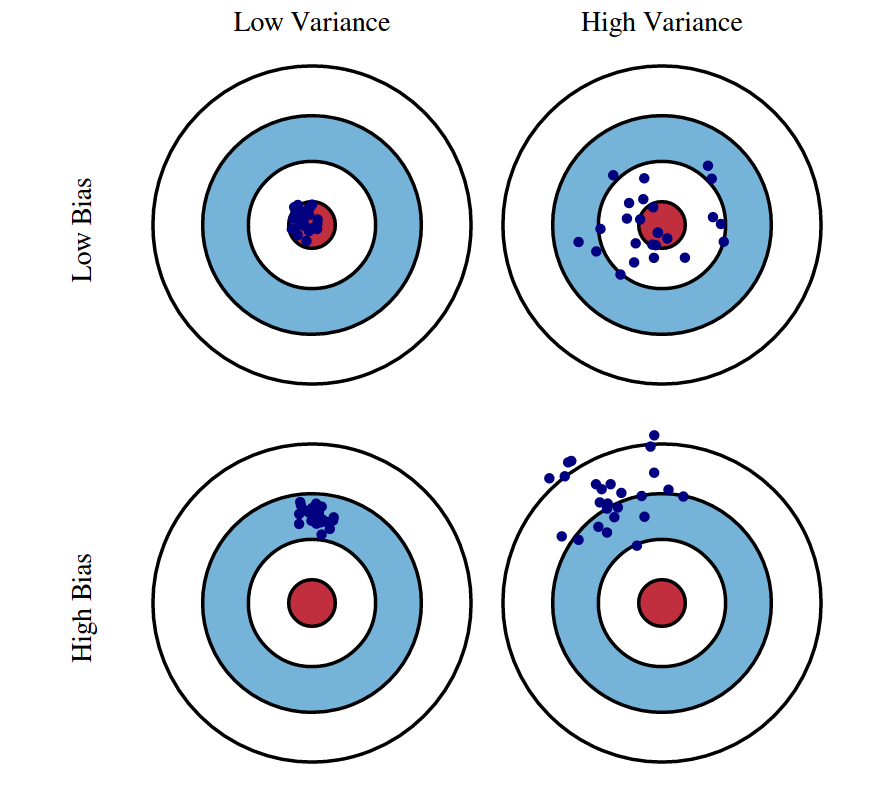Bias와 Variance의 trade-off편향값과 분산값에 따른 설명을 그림으로 나타낸것인데 편향값이 크면 중앙에서 멀어지게 되고(실제값과 예측값의 차이가 큼) 작으면 중앙에 가까워진다(실제값과 예측값이 비슷함). 분산의 경우 분산값이 크면 x끼리 거리가 멀어지고(예측값이 큰 범위를 가짐) 작으면 x끼리 뭉쳐있는 것을 확인할 수 있다(예측값의 범위가 작음)
참조
Bias-Variance tradeoff, Wikipedia
Bias-Variance Trade-off(편향-분산 트레이드 오프) 이해 그리고 머신러닝 학습 정도 이해 :: Data 쿡북
Bias-Variance Decomposition, ratsgo’s blog
머신 러닝 편향-분산 트레이드오프 (Bias-Variance Tradeoff)
연세대학교 원주캠퍼스 인공지능 강의
