SVM(Support Vector Machine)

lolhi·2021년 3월 1일

ML

목록 보기

2/3

Support Vector Machine

Support Vector Machine이란

Support Vector Machine, 한글로 번역해보면 지지 벡터 머신이라고 하는데 솔직히 이름만 봐서는 잘 감이 오지 않는다. 다음 예시를 통해 Support Vector Machine을 이해해보도록 하자.
출처: https://github.com/rickiepark/handson-ml

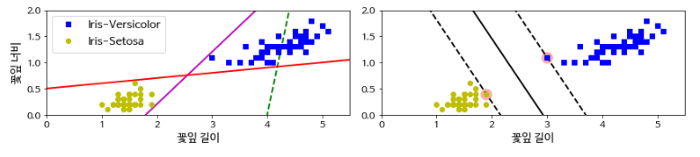
붓꽃 데이터셋중 Iris-Vesicolor종과 Iris-Setosa종을 도식화 하였다. 각 종에 따라 차이점을 명확하게 확인할 수 있다. 그래서 이 두종을 분류해보기로 한다.

먼저 왼쪽의 그림을 보면 점선을 제외한 나머지 두개의 직선이 Versicolor종과 Setosa종을 잘 분류하는 것을 확인할 수 있다. 하지만 두 직선은 당장 가지고 있는 데이터(훈련데이터)에 대해 두 종을 잘 분류할 수 있을지 몰라도 새로운 데이터(테스트 혹은 실제 데이터)에 대해서는 두 직선이 데이터와 너무 가까워(마진이 작음) 제대로 분류하지 못할 가능성이 높다. 다시 말해 일반화를 잘 하지 못할것이다.

반면에 오른쪽의 그림을 보면 왼쪽의 직선들과는 다르게 데이터와 최대한 많이 떨어져 있는 것(마진이 큼)을 확인할 수 있다. 이는 현재 가진 데이터 뿐만아니라 새로 들어올 데이터 또한 정확하게 분류할 가능성이 높다.

Support Vector Machine은 오른쪽의 경우처럼 최적의 hyperplane(초평면 또는 결정경계)을 결정하여 분류문제를 해결하려고 한다. 수많은 hyperplane 중 최적의 hyperplane을 결정하는 방법은 오른쪽의 그래프처럼 마진을 가장 크게 할 수 있는 hyperplane을 최적의 hyperplane으로 결정한다. 훈련데이터중 hyperplane에 가장 가까운 훈련데이터를 Support vector라고 하고 Support Vector에서 hyperplane과 평행하게 직선을 그은것을 Decision boundary라고 한다.

분류방법

Support Vector Machine은 다음과 같은 방식으로 분류를 수행한다.

만약 h(x)>0 이면 해당 데이터를 1로 분류하고 h(x)<0 이면 해당 데이터를 -1로 분류한다

최적의 Hyperplane 구하기

출처: https://ratsgo.github.io/machine learning/2017/05/23/SVM/

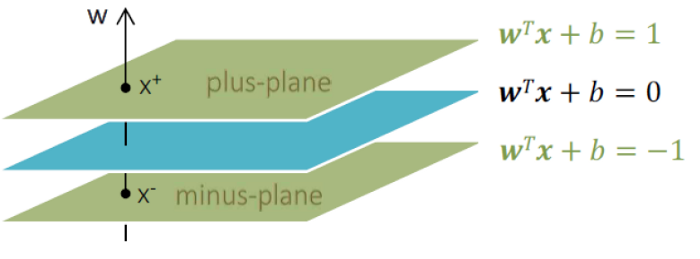
최적의 hyperplane이란 수많은 hyperplane중 마진의 크기를 가장 크게 할 수 있는 hyperplane을 의미한다. 위의 그림처럼 class 1일때 결정경계의 Support Vector와 class -1일때 결정경계의 Support Vector를 각각 $x^+$ , $x^-$ 라고 할때 다음과 같이 표현할 수 있다.

x^+=x^- +\lambda w

위 식을 이용해서 람다를 다음과 같이 유도할 수 있다.

\begin{aligned} w^Tx^+ + b = 1\\ w^T(x^- +\lambda w)+b = 1\\ w^Tx^- + b + \lambda w^Tw = 1\\ -1 + \lambda w^Tw = 1\\ \end{aligned}

\therefore\,\lambda = \frac{2}{w^Tw}

마진은 class 1일때의 결정경계와 class -1 일때의 결정경계 사이의 거리이기 때문에 다음과 같이 위의 두 식을 활용하여 마진을 유도할 수 있다.

\begin{aligned} Margin = &||x^+-x^-||_2\\ = &||x^- + \lambda w - x^-||_2\\ = &||\lambda w||_2\\ = &\lambda\sqrt{w^Tw}\\ =&\frac{2}{w^Tw}\sqrt{w^Tw}\\ =&\frac{2}{\sqrt{w^Tw}}\\ =&\frac{2}{||w||_2} \end{aligned}

이제 최적의 hyperplane을 구하기 위해 다음과 같은 최적화 문제를 해결하면 된다.

\begin{matrix} max & \large\frac{2}{||w||_2}\\ Subject\,\,to & \\&w^Tx_i + b \ge 1\,\,for\,\,y_i=1\\ & w^Tx_i + b \le -1\,\,for\,\,y_i=-1 \end{matrix}

계산상 편의를 위해 식을 바꿔보도록 하자.

\begin{matrix} min & \large\frac{||w||_2^2}{2}\\ Subject\,\,to & \\&y_i(w^Tx_i + b) \ge 1 \end{matrix}

위의 최적화 문제는 라그랑지 문제로 변환하여 해결할 수 있다.

라그랑지 승수법(Lagrange Multiplier Method)

라그랑지 승수법이란 제약식에 형식적인 라그랑지안 승수를 곱한 항을 최적화하려는 목적식에 더하여, 제약된 문제를 제약이 없는 문제로 바꾸는 기법이라고 한다. 위의 식을 라그랑지 문제로 변환하면 다음과 같은 식으로 작성할 수 있다.(이를 원문제(primal problem)이라고 표현하겠다)
(이 아래부분부터는 아직 이해를 잘 못한 상태이다. 차후에 다시 보강하도록 하겠다.)

min\,\,L_p(w,b,\alpha_i)=\frac{1}{2}||w||_2^2 - \sum_i\alpha_i[y_i(w^Tx_i + b) - 1]

위의 식에서 Karush-Kuhn-Tucker(KKT)조건을 적용하면 아래와 같은 식들을 얻을 수 있다.

\begin{aligned} 1.&\,\,\frac{\partial L}{\partial w} = w - \sum_i\alpha_iy_ix_i = 0\\ 2.&\,\,\frac{\partial L}{\partial b} = \sum_i\alpha_iy_i = 0\\ 3.&\,\,\alpha_i[y_i(w^Tx_i + b) - 1] = 0\\ 4.&\,\,y_i(w^Tx_i + b) - 1 = 0\\ 5.&\,\,\alpha_i \ge 0 \end{aligned}

원문제의 목적함수는 convex(볼록)이고 제약식 또한 convex이기 때문에 위 식의 KKT 조건은 원문제 해에 대한 필요충분조건을 제공한다고 한다. 따라서 위 식을 통해 다음과 같은 값을 얻을 수 있다.

w = \sum_i\alpha_iy_ix_i

또한 KKT조건중 5번째 조건을 만족하는 임의의 $i$ 에 대해서 KKT조건 3번째를 이용하여 다음과 같은 값을 얻을 수 있다.

b=\frac{1 - w^Tx_i}{y_i},\,\,\,\,\,\,\alpha_i \ge 0

$\alpha_i>0$ 인 i가 하나만 있는 것은 아니기 때문에 $b$ 값이 데이터에 따라 다르게 나올 수 있다. 일반적으로 구한 $b$ 값의 평균을 사용하는것이 최적의 값으로 알려져 있다고 한다.

마지막으로 위 두 값을 구하기 위해서는 a를 구해야 한다. a값을 구하기 위해선 위의 라그랑지 문제에 KKT조건 1번을 넣어 울프쌍대문제(Wolfe Dual Problem)으로 변환하여 구할 수 있다.

\begin{matrix} max & \large L_p = \sum_i \alpha_i - \frac{1}{2}\sum_i\sum_j\alpha_i\alpha_jy_iy_jx_i^Tx_j\\ Subject\,\,to & \\ &\sum_i\alpha_iy_i = 0, \,\, \alpha \ge 0, \,\, i=1...N \end{matrix}

위 문제는 목적함수가 a에 대해 이차이고 제약조건이 선형이므로 이차계획법(quadratic programming)문제이다. 이차계획법을 이용하여 위 문제를 해결하면 a를 구할 수 있고, 이를 이용해서 w,b값을 구하면 최적의 hyperplane을 구할 수 있다.

분리 불가능한 선형 SVM

출처: https://github.com/rickiepark/handson-ml

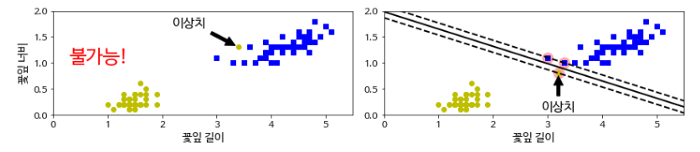
위의 문제처럼 항상 선형 SVM으로 분리가 가능하면 좋겠지만 아쉽게도 모든 데이터가 그렇지는 않다. 위의 왼쪽 그림처럼 아예 분리가 불가능 하거나 오른쪽 그림처럼 분리는 가능하지만 이상치 때문에 마진이 작아져 일반화가 어려워지는 문제가 있다.
출처: https://ratsgo.github.io/machine learning/2017/05/29/SVM2/

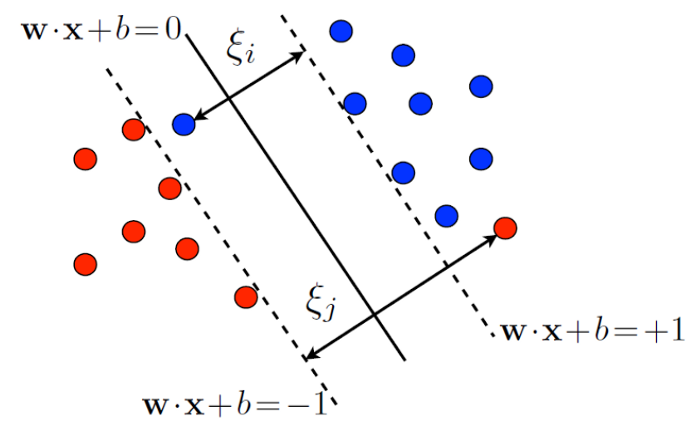
위의 문제를 해결하기 위해서는 그림과 같이 여유변수(slack variable) ξ를 추가해주면 해결이 가능하다. 여유변수 ξ를 추가하여 어느정도 오분류를 허용하는 것이다. 이를 위한 최적화 문제는 다음과 같이 변형된다.

\begin{matrix} min & \large\frac{||w||_2^2}{2}+C\sum_i^N\xi_i\\ Subject\,\,to & \\&y_i(w^Tx_i + b) \ge 1\\ &\xi \ge 0 \,\,\forall\,\,i \end{matrix}

다시말하면 마진밖에 다른 범주의 객체가 놓이는 것을 허용하지만 만약 실제로 다른범주가 놓이게 되면 여유변수 ξ에 비례하여 페널티를 주는것이다. 위 식에서 C값이 페널티 단가이다.
위 식을 울프쌍대문제로 변환하게 되면 아래와 같다.

\begin{matrix} max & \large L_p = \sum_i \alpha_i - \frac{1}{2}\sum_i\sum_j\alpha_i\alpha_jy_iy_jx_i^Tx_j\\ Subject\,\,to & \\ &\sum_i\alpha_iy_i = 0, \,\, 0 \le \alpha \le C, \,\, i=1...N \end{matrix}

하드마진의 울프쌍대문제와 목적식은 동일하며 제약식의 α의 값의 제약식만 바뀐것을 확인할 수 있다.
일반적으로 분리가 가능한 선형 SVM을 하드마진(hard margin)또는 최대마진(maximal margin)이라고 부르는 반면에 분리불가능한 선형 SVM의 경우 소프트 마진(soft margin)이라고 부른다.

참조

초짜 대학원생의 입장에서 이해하는 Support Vector Machine (1), Jaejun Yoo
서포트 벡터 머신 (Support Vector Machine), ratsgo
라그랑주 승수법 (Lagrange Multiplier Method), ratsgo
C-SVM, ratsgo
연세대학교 미래캠퍼스 데이터마이닝 수업자료, 성태응
데이터마이닝 기법과 응용, 전치혁
Hands On Machine Learning

lolhi

Machine Learning/Deep Learning/Clinical Informatics/Finance Analysis

이전 포스트

Bias-Variance trade-off

다음 포스트