비선형 SVM

lolhi·2021년 3월 6일

ML

목록 보기

3/3

지난글을 통해서 선형 SVM과 소프트마진 분류에 대해서 공부하였다. 선형 SVM은 비선형 SVM에 비해 효율적이고 많은 경우에서 잘 작동하지만 선형적으로 분류할 수 없는 데이터에 대해서는 정상적으로 동작하지 않는다. 이번글을 통해서 비선형 SVM 방법론에 대해서 공부해보고자 한다.

비선형 SVM 분류

비선형 SVM 분류는 말 그대로 비선형적인 데이터에 대하여 최적의 초평면을 찾아 이들을 분류하는 것을 의미한다. 일반적인 선형 SVM으로는 분류할 수 없고 특정 방법을 사용하여 분류할 수 있다.

1. 다항 특성 추가

가장 쉽게 생각할 수 있는 방법은 특성에 다항특성을 추가해주고 선형 SVM을 이용하여 분류하는 방법이 있다.
출처: https://github.com/rickiepark/handson-ml/blob/master/05_support_vector_machines.ipynb

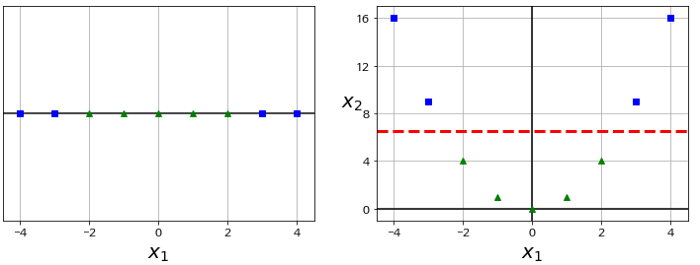
위의 왼쪽 그래프에서는 선형 SVM으로 분류할 수 없지만 왼쪽 그래프에 $X^2$ 특성을 추가해주면 오른쪽 그래프처럼 변해 선형 SVM으로 분류할 수 있다. Python을 이용해 다음과 같이 구현할 수 있다.

from sklearn.datasets import make_moons
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import PolynomialFeatures

polynomial_svm_clf = Pipeline([
        ("poly_features", PolynomialFeatures(degree=3)),
        ("scaler", StandardScaler()),
        ("svm_clf", LinearSVC(C=10, loss="hinge", max_iter=2000, random_state=42))
    ])
polynomial_svm_clf.fit(X, y)

Scikit learn의 PolynomialFeatures를 사용해 다항특성을 추가해주고 StandardScaler를 통해 정규화를 해준다. 마지막으로 LinearSVC를 이용하여 선형 SVM으로 분류를 수행한다.
출처: https://github.com/rickiepark/handson-ml/blob/master/05_support_vector_machines.ipynb

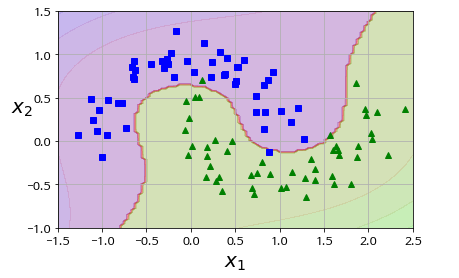
위의 코드를 사용하여 Moon dataset(데이터 분포모양이 위 그림과 같음)에 대해 SVM을 수행하면 다음과 같은 결과를 얻을 수 있다.

위에서 보다시피 다항식 특성을 추가하는 것은 간단하고 대부분 정상동작하지만 낮은 차수의 특성은 데이터를 잘 표현하지 못할 가능성이 높고 높은 차수의 특성은 너무 많은 다항특성을 추가해 계산복잡도가 높아진다.

2. Kernel Trick

다항특성 추가는 간단하고 대부분의 경우에서 잘 작동하지만 차수가 높아질수록 계산량이 폭증한다는 치명적인 단점이 있다. 계산량이 증가하게 되면 그만큼 최적의 초평면을 구하는데 오래걸리기 때문에 다른 방법을 사용해야 한다.

다행히도 Kernel Trick이라는 수학적 기교를 사용하여 변환 함수의 정보없이 실제로 다항 특성을 추가 하지않더라도 다항특성을 여러개 추가한것과 같은 결과를 얻을 수 있다.

다항식 커널을 사용하기 위해 다음과 같이 초평면을 정의한다.

f(x)=\Phi(x)^Tw + b

이때 $\Phi(x)$ 를 $p$ 차원의 $x$ 를 그보다 높은 $m$ 차원으로 매핑하는 기저함수(basis function)라고 할때 최적의 초평면을 구하기 위한 울프쌍대문제는 다음과 같이 정의된다.

\begin{matrix} max & \large L_p = \sum_i \alpha_i - \frac{1}{2}\sum_i\sum_j\alpha_i\alpha_jy_iy_j\Phi(x_i^T)\Phi(x_j)\\ Subject\,\,to & \\ &\sum_i\alpha_iy_i = 0, \,\, 0 \le \alpha \le C, \,\, i=1...N \end{matrix}

여기서 울프쌍대문제를 해결하기 위해 필요한것은 $\Phi$ 함수의 정보가 아닌 $\Phi$ 의 내적인것을 확인할 수 있다.

다음과 같은 2차 다항식이 있다고 가정해보자

\Phi(x)=\Phi \begin{pmatrix} \begin{pmatrix} x_1 \\ x_2 \end{pmatrix} \end{pmatrix} = \begin{pmatrix} x_1^2 \\ \sqrt{2}x_1x_2 \\ x_2^2 \end{pmatrix}

$\Phi$ 함수의 내적은 다음과 같이 표현할 수 있다.

\begin{aligned} \Phi(a)^T\cdot\Phi(b) = & \begin{pmatrix} a_1^2 \\ \sqrt{2}a_1a_2 \\ a_2^2 \end{pmatrix} \cdot \begin{pmatrix} b_1^2 \\ \sqrt{2}b_1b_2 \\ b_2^2 \end{pmatrix}\\ = & \,a_1^2b_1^2 + 2a_1b_1a_2b_2 + a_2^2b_2^2\\ = & \,(a_1b_1 + a_2b_2)^2\\ = & \begin{pmatrix} \begin{pmatrix} a_1 \\ a_2 \end{pmatrix} \cdot \begin{pmatrix} b_1 \\ b_2 \end{pmatrix} \end{pmatrix}^2 \end{aligned}

a,b의 내적은 다음과 같이 표현할 수 있다.

a^T\cdot b = \begin{pmatrix} \begin{pmatrix} a_1 \\ a_2 \end{pmatrix} \cdot \begin{pmatrix} b_1 \\ b_2 \end{pmatrix} \end{pmatrix}^2

따라서 a,b를 고차원으로 매핑하는 Φ함수의 내적결과와 a,b의 내적결과가 같다는 것을 알 수 있다. 이러한 성질을 Kernel Trick이라고 한다.

이러한 성질을 만족하는 Kernel은 여러가지 있다.

가우시안 RBF(Radial Basis Function) $K(a,b)=exp(-\gamma||a-b||^2)$
r차 다항커널 $K(a,b)=(a^Tb+1)^r$
시그모이드 커널 $K(a,b) = tanh(ka^Tb - \delta)^r$

2.1 다항식 커널

Python을 이용해 다음과 같이 구현할 수 있다.

from sklearn.svm import SVC

poly_kernel_svm_clf = Pipeline([
        ("scaler", StandardScaler()),
        ("svm_clf", SVC(kernel="poly", degree=3, coef0=1, C=5))
    ])
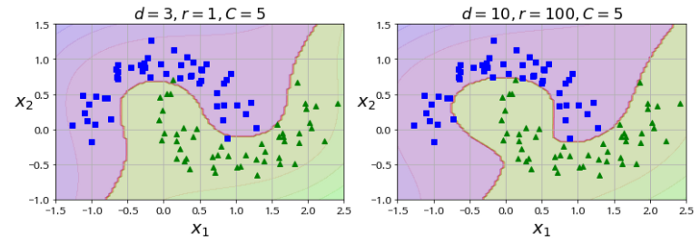
poly_kernel_svm_clf.fit(X, y)

Moons dataset에 kernel trick을 사용하여 3차 다항식 커널을 적용하여 훈련 시킨다. 이는 실제 다항특성을 추가한 SVM과 같은 결과를 얻지만 Kernel Trick을 사용하였기 때문에 빠를것이다.

출처:https://github.com/rickiepark/handson-ml/blob/master/05_support_vector_machines.ipynb

2.2 유사도 함수

비선형 특성을 다루는 또 다른 기법은 각 샘플이 특정 랜드마크와 얼마나 닮았는지 측정하는 유사도 함수로 계산한 특성을 추가하는 것이다.

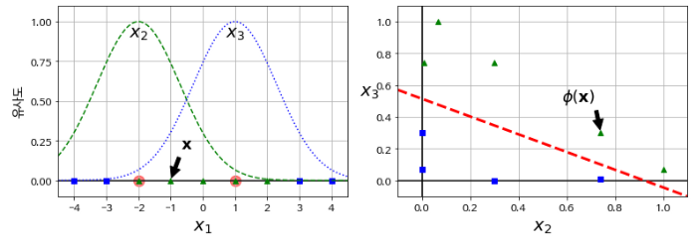
예를 들어 다항 특성 추가에서 사용하였던 예제에 $x1=-2, x1=1$ 을 추가하고 이 둘을 랜드마크로 지정 후 유사도 함수로는 $\gamma = 0.3$ 인 가우시안 RBF로 정의한다고 하자.
출처: https://github.com/rickiepark/handson-ml/blob/master/05_support_vector_machines.ipynb

가우시안 RBF를 이용하여 다시 값을 고차원으로 매핑하게 되면 다음과 같이 선형으로 데이터를 분류할 수 있다.

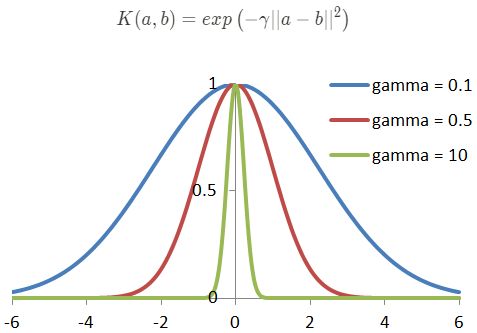
가우사안 RBF(Radial Basis Function)
출처: https://tomaszkacmajor.pl/index.php/2016/04/24/svm-model-selection/

가우시안 RBF의 값은 랜드마크와의 거리에 따라 0(아주 멀리 떨어짐)~1(아주 가까움) 사이의 값을 가진다. 또한 gamma의 값에 따라 종모양의 크기가 정해진다.

Python을 이용해 다음과 같이 가우시안 RBF를 사용해볼 수 있다.

rbf_kernel_svm_clf = Pipeline([
				("scaler", StandardScaler()),
				("svm_clf", SVC(kernel="rbf", gamma=5, C=0.001))
])
rbf_kernel_svm_clf.fit(X, y)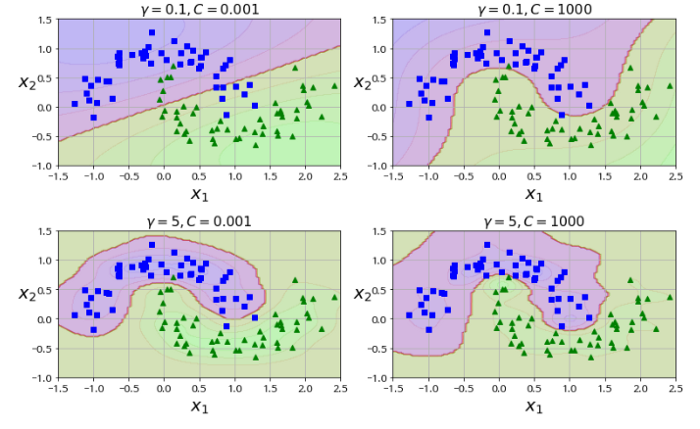

출처: https://github.com/rickiepark/handson-ml/blob/master/05_support_vector_machines.ipynb

참조

Hands On Machine Learning, Aurélien Géron
데이터마이닝 기법과 응용, 전치혁
Kernel-SVM, ratsgo

lolhi

Machine Learning/Deep Learning/Clinical Informatics/Finance Analysis

이전 포스트