설명가능한 AI

모델을 해석한다는 것의 의미, 모델의 과정을 알기 위해서…

• 모델들의 복잡도가 증가하면서, 블랙박스 모델의 해석이 더 어려워짐

• 다양한 알고리즘을 동일한 기준으로 해석할 필요성 生

어떠한 모델을 사용하더라고 Input과 Output이 존재하기 마련

---

Permutation Importance

특정 피처의 중요도를 평가하기 위해, 해당 피처의 값을 무작위로 섞어서 모델 성능이 얼마나 떨어지는지 측정하는 방법.

• 특정 Feature 값들을 임의로 섞으면 모형 성과는 얼마나 나빠질까

  • 임의의 값들에 대해서 생소한 Random 값보다 실제 있을법한 기존 값들을 재배치하자

• 모형성과는..?

  • 재학습하지 말고 기존의 학습된 모형에 Original set VS Permutation set을 예측하여 오차를 비교

예시 흐름:

1. 원래 테스트 데이터를 모델에 넣어서 성능 측정

2. 한 피처의 값을 무작위로 섞음 (→ 이게 "Permutation set"이 된 데이터)

3. 모델에 다시 넣어서 성능 재측정

4. 성능이 얼마나 떨어졌는지를 통해 그 피처가 중요한지를 판단

---

용어	의미
Permutation set	특정 피처(column)의 값을 무작위로 섞은 데이터셋 (다른 변수들의 값은 고정)
목적	그 피처가 모델 예측에 얼마나 기여하는지 확인
관점	"이 피처 없으면 예측이 얼마나 망가지냐?"를 보려는 것

---

• 요약

항목	설명
의미	피처의 값을 랜덤으로 섞은 데이터셋
사용 목적	모델이 해당 피처에 얼마나 의존하고 있는지 측정
장점	모델 내부를 열어보지 않고도 피처 중요도 추정 가능 (Black-box 모델에서도 사용 가능)
적용 도구	scikit-learn, eli5, SHAP 등에서 지원

---

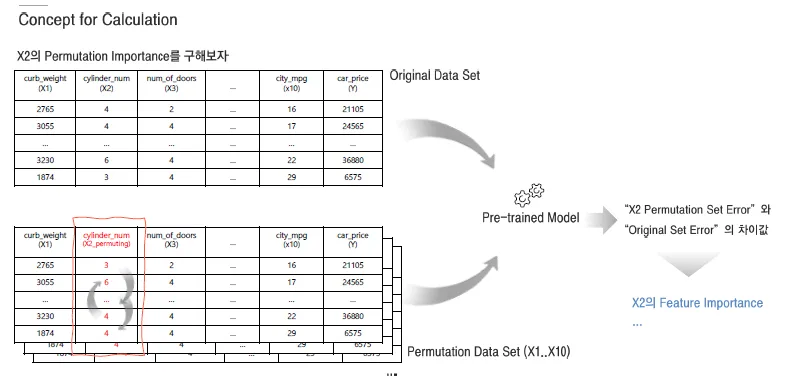
이런 과정을 통해서 각 Feature에 대한 Importance를 얻을 수 있음

---

하지만, 이러한 중요도를 구하는 과정을 어떤 데이터를 사용해야 할까?

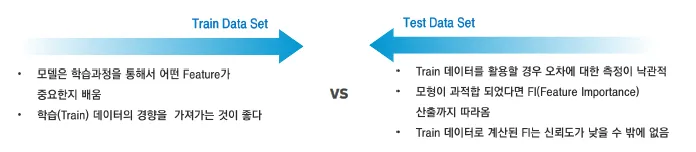
장점

• 모델을 재학습할 필요가 없기 때문에 계산 비용의 장점

• 비교가 용이한 직관적인 Feature 중요도를 얻음

• Feature 간의 상호작용이 자동적으로 고려됨

단점

• 영향의 방향은 알 수 없음

• Outlier가 있다면 편향될 수 있음

• 알고리즘 실행 시마다 중요도는 다르게 계산될 수 있음(Permutation 정도에 따라서..)

• 상관관계가 높은 Feature가 포함되어 있다면 중요도가 왜곡될 수 있음

---

Surrogate Model

현재 모델의 예측력을 사용하면서, 가볍고 해석가능한 대리 모델의 설명력을 활용

해석이 어려운 블랙박스 모델의 예측에 근사하도록 훈련된 해석가능한 대리모델 사용하여 블랙박스 모델에 대한 설명력을 제공

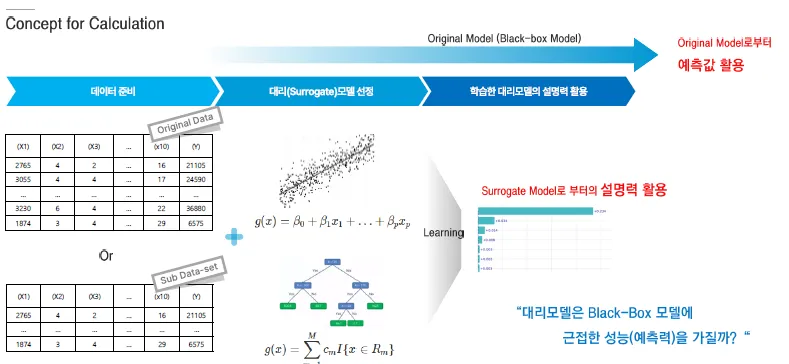
• Sub Data set

데이터를 대표할 수 있는 데이터들(대표표본)

대리모델이 Original에 가까운지를 측정

• 선형모델

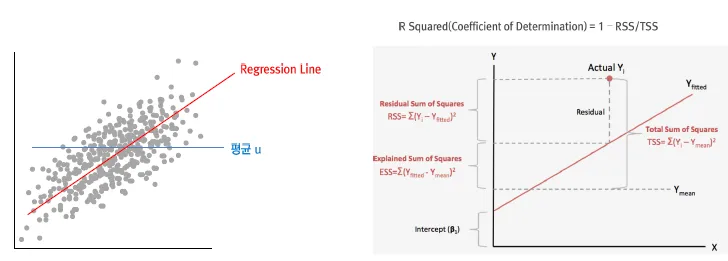
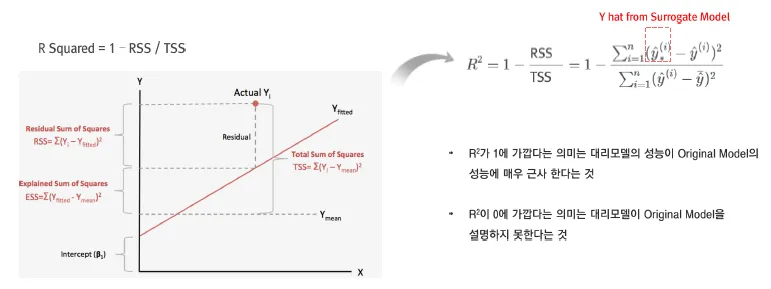
0~1의 스케일로 회귀식의 설명력을 표현하는 것과 같은 구조로 표현

---

장점

• 해석이 가능하면 어떤 모델이든지 사용할 수 있는 유연함

• 사용자와의 접근성에 따라 대리 모델을 선택할 수 있고, Multi-Surrogate 모델 구성 등 설명력의 제공 방식이 열려 있음

  Ex) D/L계열의 Original 모델을 통해 예측력 제공 + 선택/Tree 2가지 대리모델을 통해 다각도 설명력을 제시

  Ex) 평소 회귀분석 결과로 Comm.을 하던 업무방식 → 선택 대리모델을 통해 설명력을 제공
  

---

단점

• 대리모형과 Original 모델의 근사함을 판단하는 기준이 명확치 않음.. R2 0.5? 0.8? 0.99?

• 어떤 Sample에서는 대리모델과 Original 모델과 근사하지만, 어떤 Sample에서는 크게 다를 수 있음

• 해석력은 모든 데이터 포인트에 대해 동의하지 않음

---

---

LIME, Local Interpretable Model-agnostic Explanation

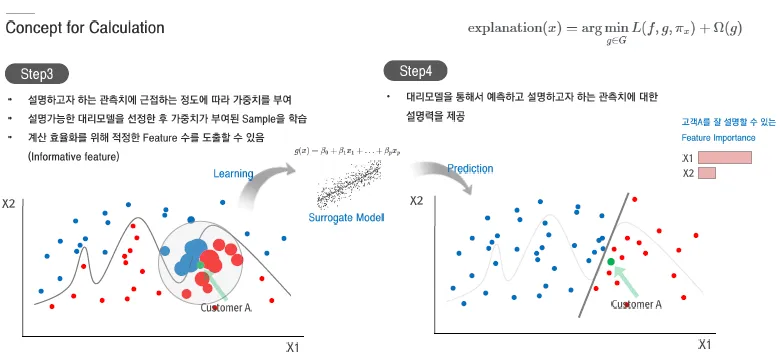
설명하고자 하는 관측치에 초점을 맞춰서 해석가능한 대리 모델을 활용

• 해석의 초점을 바꾸어서 해당 관측치의 개별 예측을 보다 잘 설명할 수 있음

• Local Surrogate Model

• 비선형적인 패턴을 학습한 모형이더라도 국소적으로 보면 선형 모형으로 설명할 수 있음

---

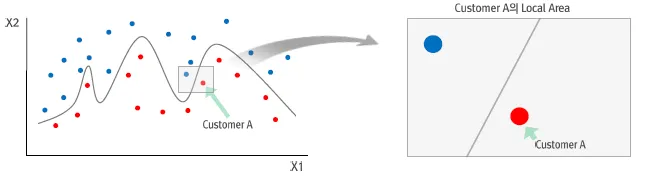
Local Surrogate Model은 왜 필요할까?

• 전체의 경향이 아닌 개별 Instance에 대한 해석과 원인 분석이 용이

• 개별 Instance(개별 고객,..)에 대한 해석력을 제공함으로써 높은 활용성

• 기존(As-Is) 모형은 잘 맞추는데 신(To-Be) 모형에서는 예측을 잘 못하는 특정 Case가 있다면..

• 기존 데이터 분포와 다른 새로운 Instance의 영향 파악해야 한다면..

---

---

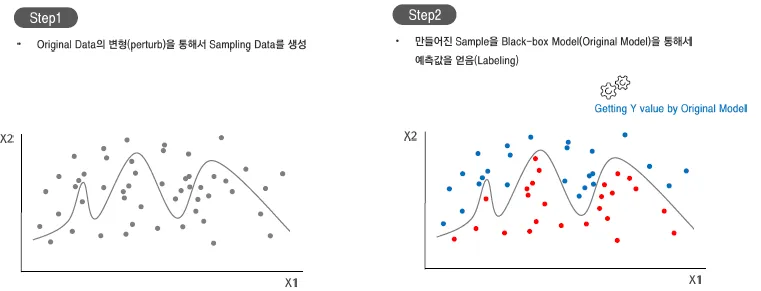
장점

• 기존 학습 모델을 교체하더라도 로컬 대리 모델을 사용하여 동일한 설명력을 제공할 수 있음

  Ex) "Decision Tree" 방식의 설명력 제공에 익숙한 사용자, 기존 모델(SVM)보다 더 나은 예측력을 제공하는 신모델(DL)이 있을 때, SVM모델을 교체하더라도 “Decision Tree”의 설명력을 계속 제공할 수 있음
  

• Local Surrogate Model을 통해서 해석에 중요한 Feature로 설명력을 제공할 수 있음

  Ex) Black-box Model은 PCA(주성분), 변수변환에 의한 Feature를 사용하여 예측값을 제공하지만, Local Surrogate Model은 Black-box Model이 생성한 Feature와 다르게 원본 Feature를 활용한 설명력을 제공할 수 있음
  

• Image, Text 등 비정형 데이터에 대해서도 유연하게 작동

---

단점

• 해석에 큰 영향을 주는 이 요인에 대한 직접적인 정의는 해결하기 어려운 문제

  • 이웃에 대한 적절한 정의가 어려움

• Gaussian 분포에서 제공되는 샘플들은 Feature간의 상관관계를 반영하기 어려움

• 같은 관측값임에도 대리모형이 만들어질 때마다(D/Sampling 될 때마다) 결과가 상이할 수 있음 (Sample size를 늘려라..)

---

SHAP, SHapley Additive exPlanations

(1) Shapley Value

Feature 조합의 모든 경우의 수를 고려

Game Theory

• 상대방의 행위가 자신의 이익에 영향을 미칠 경우 이와 관련해 이익을 극대화 하는 최선의 의사결정에 대한 연구

• 상대방의 결정에 상관없이 취할 수 있는 최선의 전략 → Dominant Strategy

• 각 참가자의 전략이 주어져 있을 경우 → Nash Equilibrium

• 각 참가자가 협조적일 때 (Win-Win) 최선의 전략 → Cooperative Game (Stable allocations)

• …

---

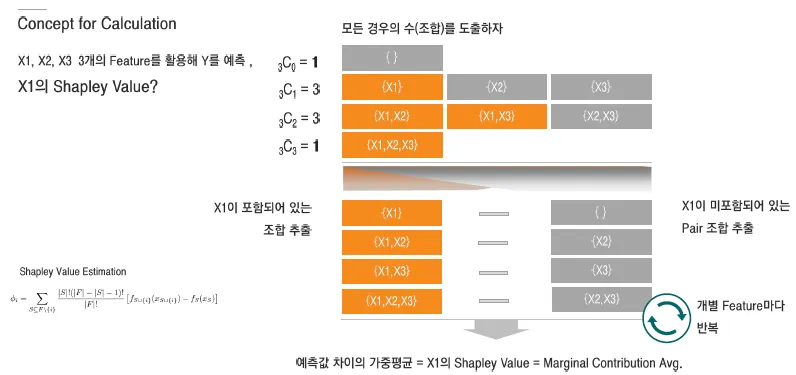
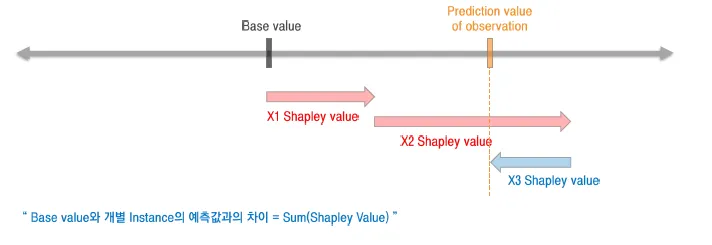
조합의 수만큼 계산해야하므로, 계산량이 기하급수적으로 증가함 2^(n)

---

장점

• 예측값(Y)을 결정하는 기준을 균형있게 해석할 수 있음

• Feature간 의존성을 고려해서 모델 영향력을 계산 (Multicollinearity)

• 음의 영향력을 고려할 수 있음 (Negative Feature Importance)

  • 방향성을 가짐

• Feature 값에 따라 Y가 어떻게 변화하는지 설명이 가능

---

단점

• Feature 수에 따라 기하급수적으로 늘어나는 연산비용

• 연산비용의 한계로 Sample 계산량을 줄이면 오차의 분산이 커짐

• 이상치/새로운 데이터에 대해 허술한 해석을 내놓을 가능성

---

SHAP의 해석

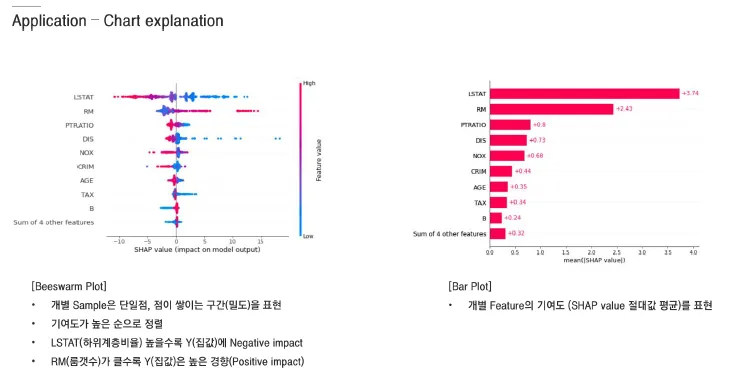
Dataset: 집 값 예측을 위한 변수들

• X축: SHAP Value

  • 0을 기준으로 양/음수

    • 양: y값에 양의 방향으로 영향을 줌
    • 음: y값에 음의 방향으로 영향을 줌

• Y축 : 변수들(중요한 순서대로)

• 색상: 절대적인 값의 크고 작음(빨간색 : 크다/ 파란색 : 작다)

---