해당 미니 프로젝트는 실제로 sk 내에서 진행했던 경진대회? 느낌의 프로젝트이다.
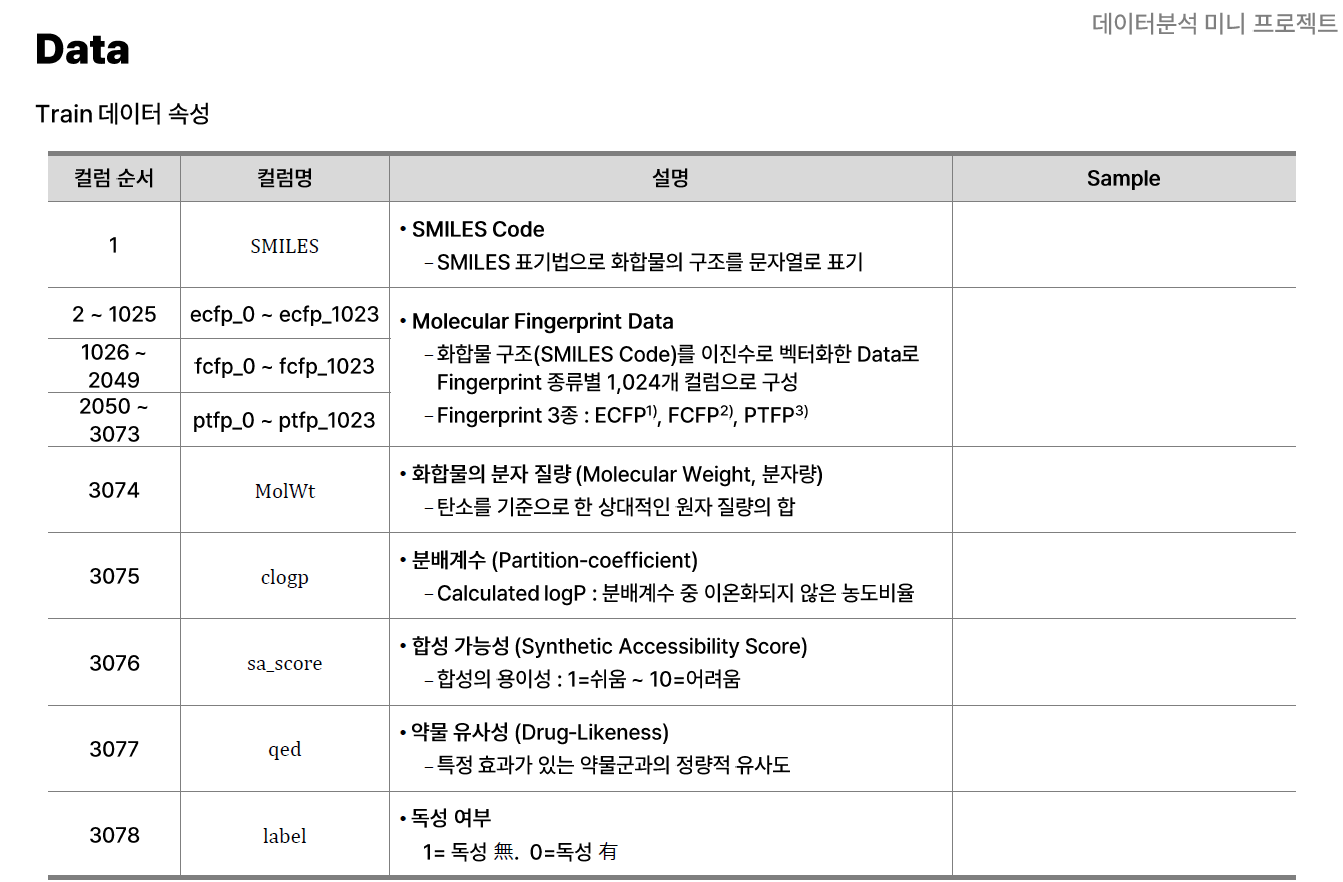
위의 표와 같이 데이터는 총 3078개의 Column으로 이루어져 있었고, 데이터의 총 수는 약 8300개 가량이었다.
데이터의 수가 매우 적으며, 차원의 수가 매우 많은 데이터의 특성을 가짐
아래와 같이 세 개의 표로 정리할 수 있다.
| 구분 | 내용 |
|---|---|
| 총 샘플 수 (행) | 8,349개 |
| 총 변수 수 (열) | 3,078개 |
| 구분 | 설명 |
|---|---|
| SMILES | 분자의 화학 구조를 문자열로 표현한 정보 (문자형 object) |
| Fingerprint | ecfp_, fcfp_, ptfp_로 시작하는 이진 벡터 (총 3,072개, 각 1,024개씩) |
| 특성 변수 | MolWt, clogp, sa_score, qed (분자량, 지용성, SA 점수, QED) – 연속형 (float64) |
| 라벨 | label – 예측 대상(예: 독성 여부)로 추정 (int64 또는 범주형) |
| 이름 | 설명 |
|---|---|
| ECFP (Extended Connectivity Fingerprint) | 분자의 부분 구조에 대한 정보 원자 간 연결관계 기반의 구조적 특징 |
| FCFP (Functional-Class Fingerprint) | 원자의 기능적 역할에 초점 화학적 성질 ·,작용기 기반 기능적 특징 |
| PTFP (Pattern Fingerprint) | 분자 내 특정 서브패턴의 존재 여부 표현 미리 정의된 패턴 유무를 이진 벡터로 표시 |
2초 동안 생각함
| 이름 | 설명 |
|---|---|
| MolWt (Molecular Weight) | - 분자를 구성하는 원자 질량의 총합 - 값이 클수록 분자가 무거움 |
| clogP (LogP) | - 지용성(LogP) 지표 - 값이 클수록 지질막 투과성이 높고 흡수가 잘됨 |
| sa_score (Synthetic Accessibility Score) | - 분자의 합성 용이성을 1~10 점수로 표현 - 점수가 높을수록 합성 난이도 높음 |
| qed (Quantitative Estimate of Drug-likeness) | - 약물 유사도 점수 (0~1) - 값이 높을수록 약물처럼 생김, 비독성일 가능성 ↑ |
1. 기초통계분석
결측치
print(train.isnull().sum().sum())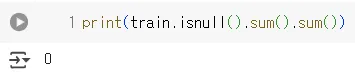
위의 이미지와 같이 결측치는 존재하지 않았다.
데이터 정보(Info & Describe)
처음에는 위에서 나왔던 3가지의 Fingerprint 를 제외하고 float 타입의 4가지 컬럼에 집중해서 EDA를 진행하고자 하였다.
print(train.iloc[:, 3073:].info())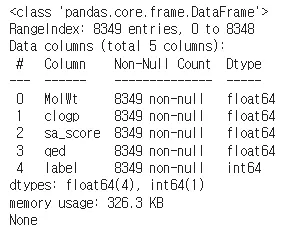
인덱싱 과정을 통해서 MolWt, clogp, sa_score, qed 컬럼이 수치형으로 이루어져 있음을 확인할 수 있었다.
print(train.iloc[:, 3073:].describe())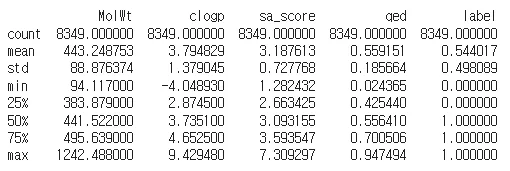
- 전체 데이터프레임에서 수치형 특성 컬럼들만 선택한 후 요약하였다.
- 해당 자료는 라벨 별로 확인할 수 없기에 라벨 별로 기초통계량을 구하는 방향으로 진행하였다.
라벨을 기준으로 컬럼 별 통계(평균, 표준편차, 최솟값, 최댓값)
이상치 탐지 및 예측 모델링을 위해, label(0: 독성, 1: 비독성) 별로,
주요 수치형 변수(MolWt, clogp, sa_score, qed)의 평균값 분포를 비교하였다.
agg_result = train.iloc[:, 3073:].groupby('label').agg(['mean', 'std', 'min', 'max'])
display(agg_result)
컬럼 별 평균값 시각화
# 평균만 계산
agg_result = train.iloc[:, 3073:].groupby('label').mean().reset_index()
# 시각화할 컬럼 목록 (label 제외)
mean_columns = agg_result.columns.drop('label')
# 시각화
agg_result.plot(x='label', y=mean_columns, kind='bar', figsize=(14, 6))
plt.title('Mean Values of All Numerical Columns by Label')
plt.ylabel('mean')
plt.xlabel('label')
plt.xticks(rotation=0)
plt.legend(title='column', bbox_to_anchor=(1.05, 1), loc='upper left') # 범례 바깥으로
plt.tight_layout()
plt.show()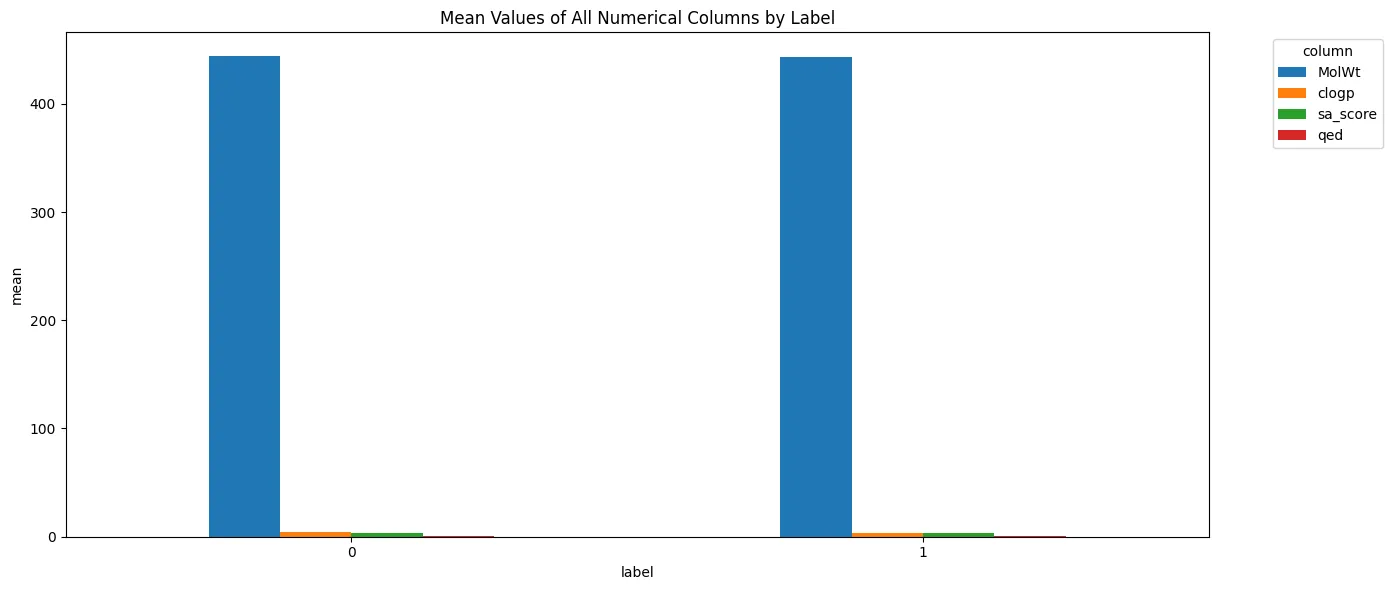
MolWt 컬럼의 수치가 커 비교가 쉽지 않았기에, 이를 각 컬럼 별로 다시 시각화하였다.
각 컬럼 별 Label 간 평균 차이
for col in mean_columns:
plt.figure(figsize=(6, 4))
# 막대그래프
sns.barplot(data=agg_result, x='label', y=col, palette=['#1f77b4', '#ff7f0e'])
# 범례 수동 추가
blue_patch = mpatches.Patch(color='#1f77b4', label='label 0')
orange_patch = mpatches.Patch(color='#ff7f0e', label='label 1')
plt.legend(handles=[blue_patch, orange_patch],
title='Label',
loc='center left',
bbox_to_anchor=(1.0, 0.5)) # 오른쪽 바깥에 위치
# 그래프 설정
plt.title(f'{col} mean')
plt.ylabel(col)
plt.xlabel('label')
plt.tight_layout()
plt.show()
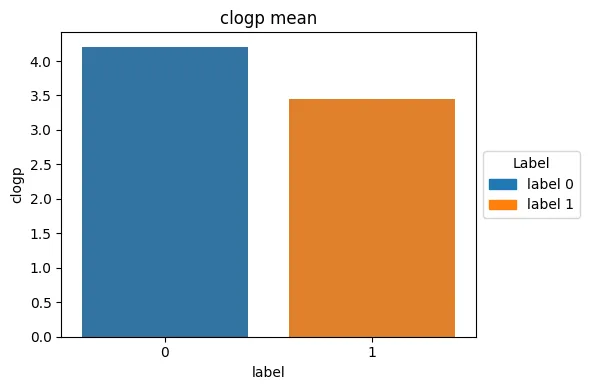
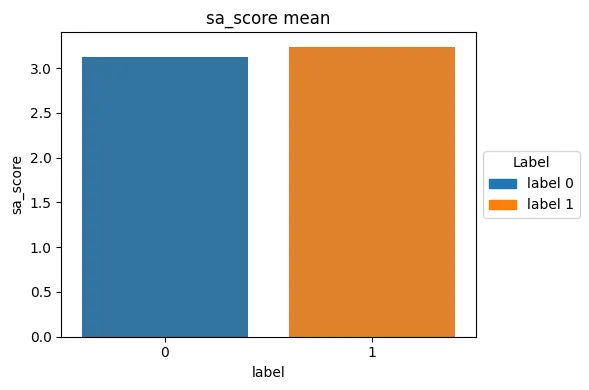
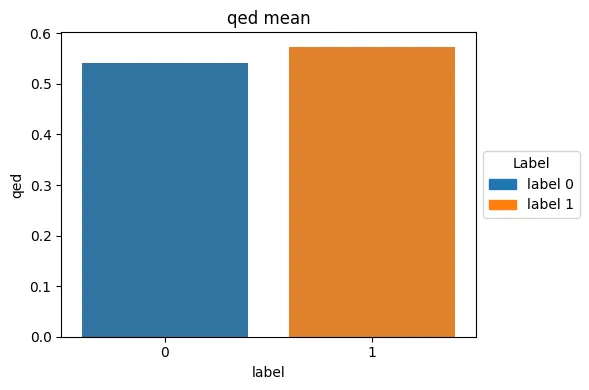
라벨 별로 각 컬럼의 평균값을 비교해 보았을 때, cloup를 제외하고 큰 차이가 없음을 확인할 수 있었다.
# 컬럼 별 평균값을 표로 출력
print("Mean Values Table:")
display(agg_result)
컬럼 별 이상치 탐지
import seaborn as sns
import matplotlib.pyplot as plt
import matplotlib.patches as mpatches # 범례용 패치
# Numeric columns only
numeric_cols = train.columns[3073:]
# Boxplot for each column by label
for col in numeric_cols[:-1]: # 마지막 컬럼 제외
plt.figure(figsize=(6, 4))
# Boxplot with custom colors
sns.boxplot(x='label', y=col, data=train, palette={"0": '#1f77b4', "1": '#ff7f0e'})
# 범례 수동 추가 (오른쪽 바깥으로)
blue_patch = mpatches.Patch(color='#1f77b4', label='label 0')
orange_patch = mpatches.Patch(color='#ff7f0e', label='label 1')
plt.legend(handles=[blue_patch, orange_patch], title='Label', loc='center left', bbox_to_anchor=(1.02, 0.5))
# 라벨 및 제목 설정
plt.title(f'{col} - Boxplot by label')
plt.xlabel('label')
plt.ylabel(col)
plt.tight_layout()
plt.show()
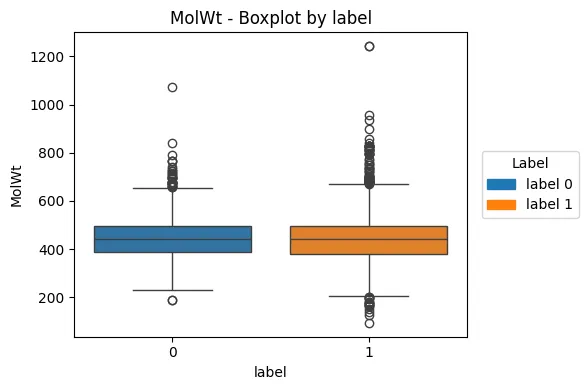
- MolWt (분자량)
- 전반적으로 분포 유사
- 비독성 화합물의 분자량이 약간 더 큼
- 매우 큰 분자(outlier)는 양쪽 모두 존재
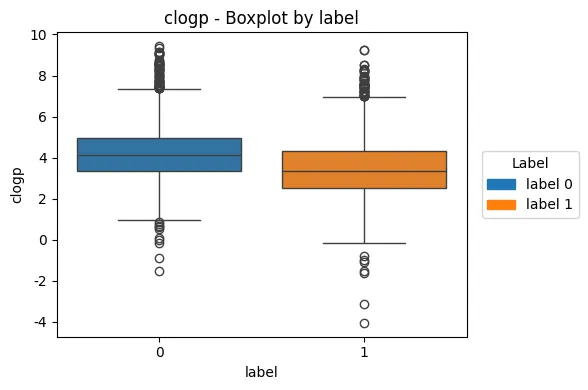
- clogp (분배계수)
- 독성 있는 화합물의 clogp가 더 높음
- 일부 label=0은 8~10 이상 outlier 존재
- clogp는 지용성 → 흡수성, 체내 분포에 영향
차후 target과의 상관관계의 분석 필요성
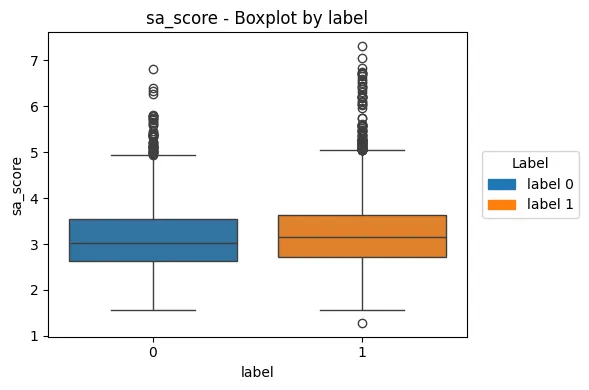
- sa_score (합성 용이성 점수)
- label=0이 평균적으로 약간 높음
- sa_score는 1에 가까울수록 합성 쉬움, 10에 가까우면 어려움
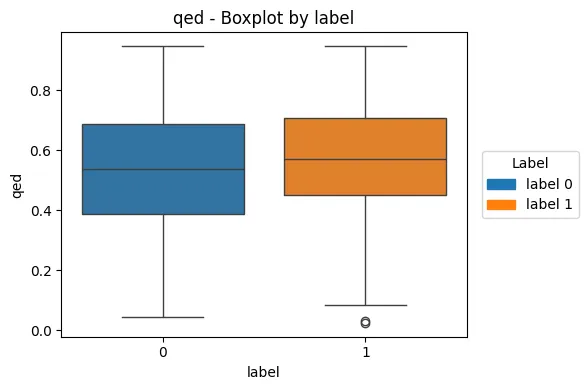
- qed
- label=1 (비독성) 쪽의 qed 값이 더 높음
- 약물 유사성이 높을수록 비독성일 가능성↑
- qed는 약물로 적합한 분자 구조 유사도를 나타냄
컬럼 별 이상치 개수
# 수치형 컬럼만 선택 (3074번째 이후)
numeric_df = train.iloc[:, 3073:-1]
# 이상치 개수 저장용 딕셔너리
outlier_counts = {}
# 각 컬럼별 이상치 계산 (IQR 기준)
for col in numeric_df.columns:
Q1 = numeric_df[col].quantile(0.25)
Q3 = numeric_df[col].quantile(0.75)
IQR = Q3 - Q1
lower = Q1 - 1.5 * IQR
upper = Q3 + 1.5 * IQR
outlier_count = ((numeric_df[col] < lower) | (numeric_df[col] > upper)).sum()
outlier_counts[col] = outlier_count
# 결과를 데이터프레임으로 변환
outlier_df = pd.DataFrame(list(outlier_counts.items()), columns=['column', 'outlier_count'])
outlier_df = outlier_df.sort_values(by='outlier_count', ascending=False).reset_index(drop=True)
# 출력
from IPython.display import display
print("Outlier Count per Column:")
display(outlier_df)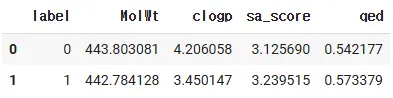
proportion
독성 물질과 비독성 물질의 비율
label
toxic 0.544017
non-toxic 0.455983
Name: proportion, dtype: float64
독성 물질(toxic)과 비독성 물질(non-toxic)의 샘플 수가 대체로 균형 있게 분포하고 있다.
2. 분포 시각화
히스토그램, KDE를 통한 분포 시각화.
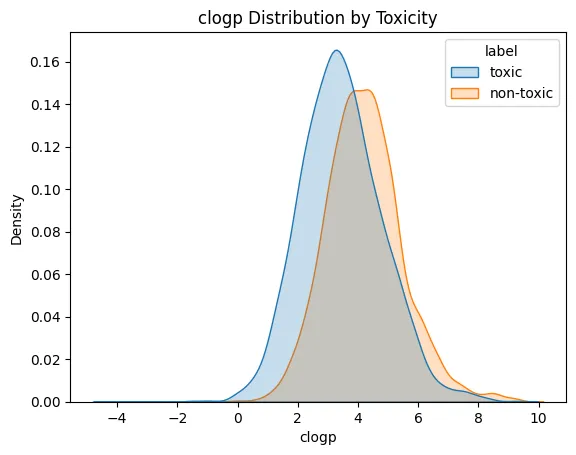
4개의 column에 대해서 위와 같이 정규분포와 비슷한 형태의 분포가 나왔으며, 라벨별로 차이를 두더라도 큰 차이를 확인하기 힘들었다
3. 상관관계 분석
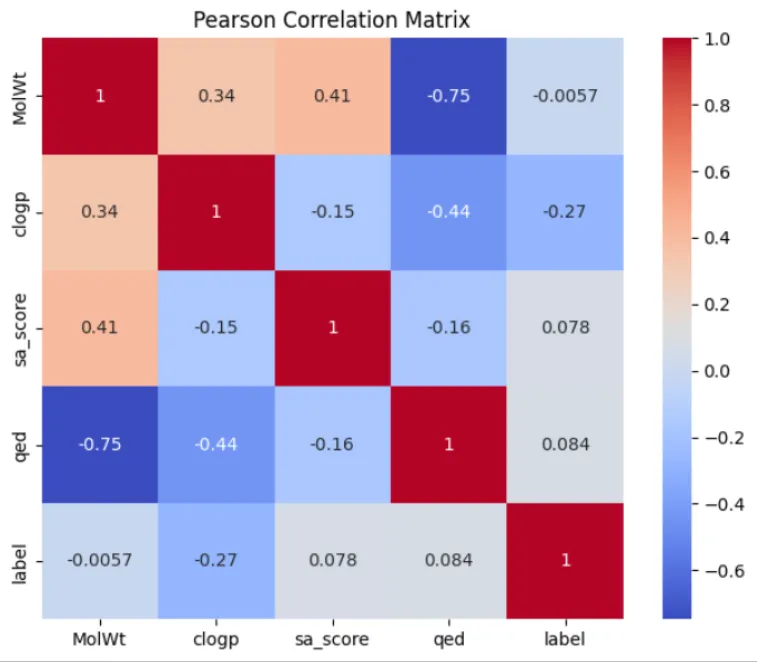
상관계수
3077개의 칼럼 중 대부분이 MoleCular Fingerprint Data와 관련 된 칼럼이고, 4개만이 다른 정보를 담고 있는 칼럼이라, 상대적으로 중요한 정보를 담고 있는 칼럼이라고 생각하고,
우선 독성(label 칼럼에 0,1로 표기됨)과의 상관관계를 뽑아보았다.
상관관계 히트맵
산점도로 개별 관계 시각화
히트맵에서는 상관계수가 낮아도, 비선형 관계나 분포 차이가 있을 수 있으므로 산점도를 통해 시각적으로 확인
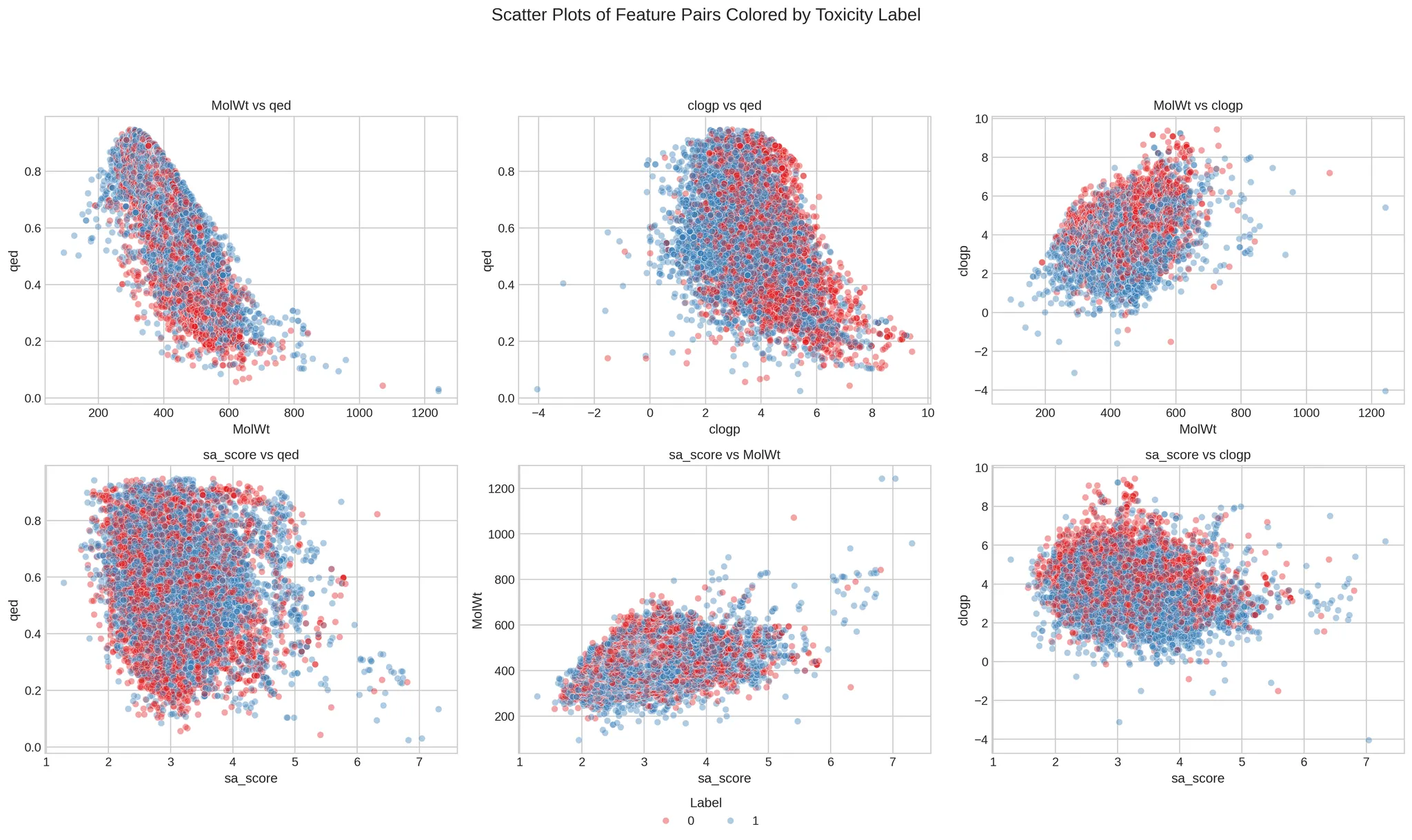
- MolWt(분자량) - qed(약물 유사성) 분자량이 클수록 약물 유사성(qed)은 낮아지는 경향이 뚜렷하며, 이 영역에 독성 화합물이 더 많이 분포하지만, 독성과 비독성을 명확히 구분짓지는 못함
- clogp(분배계수) - qed(약물 유사성) 일부 높은 clogp, 낮은 qed 조합에서 독성이 다소 많음, 독성 여부와 뚜렷한 구분은 어려움
- MolWt(분자량) - clogp(분배계수) 중간 정도의 양의 상관관계가 있으나, 독성/비독성 간 뚜렷한 구분은 없음
- sa_score(합성가능성) sa_score는 전반적으로 다른 변수들과 독성 간 구분력이 약하며, 분포 차이가 뚜렷하진 않음
즉, 처음 생각과는 달리 뒤 4개의 column은 라벨을 결정하는 데에 큰 영향을 주지 못했다.
- 원인(도메인 지식 부족)
화학·독성 분야 도메인 지식 없이 “분자량이 크면 독성이 높다” 등 단순 가설에 의존하였고, 분자의 독성 여부는 합성 용이성(sa_score)이나 약물 유사도(qed)만으로 설명하기 어려움이 존재
- 배운 점
도메인 전문가의 인사이트 없이 단순 메타 특성만으로는 복잡한 화학·독성 현상을 포착하기 어려움
모델링 전, 각 피처가 실제로 어떤 메커니즘과 연관되는지 충분히 검토해야 함
구조적 fingerprint 정보가 화학 데이터 분석에서 핵심임을 인지하고, 필요시 물리·화학 특성은 보조 피처로 활용할 것
이러한 부분을 느끼고 나서 FingerPrint에 집중하기 시작하였다
PCA, t-SNE, UMAP
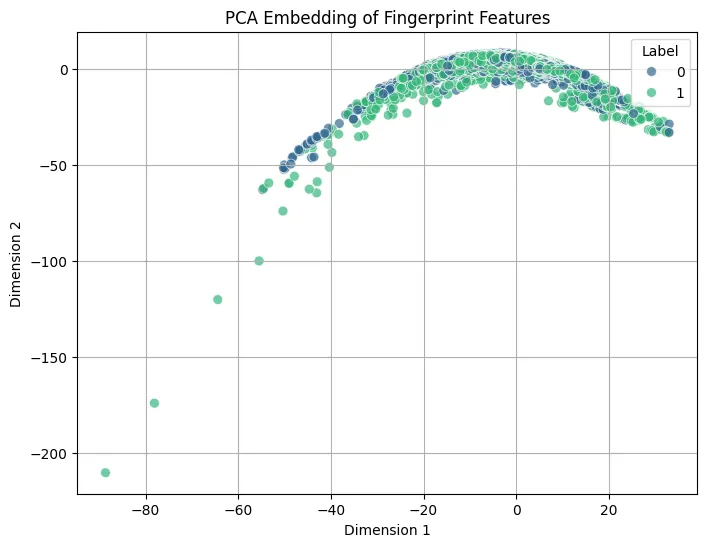
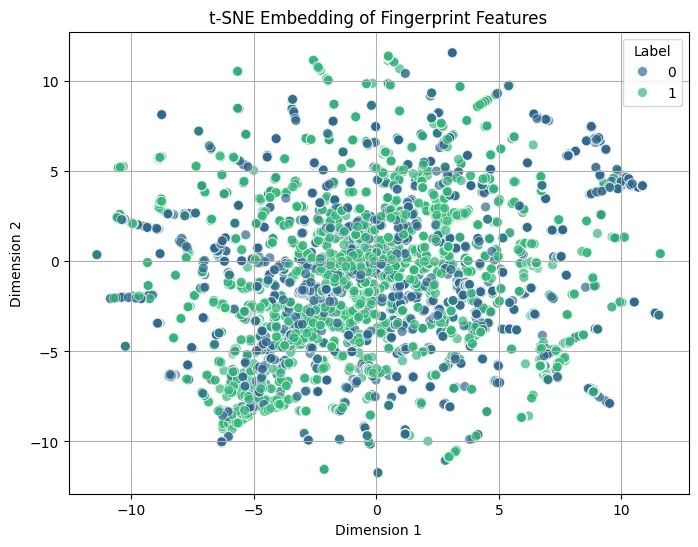
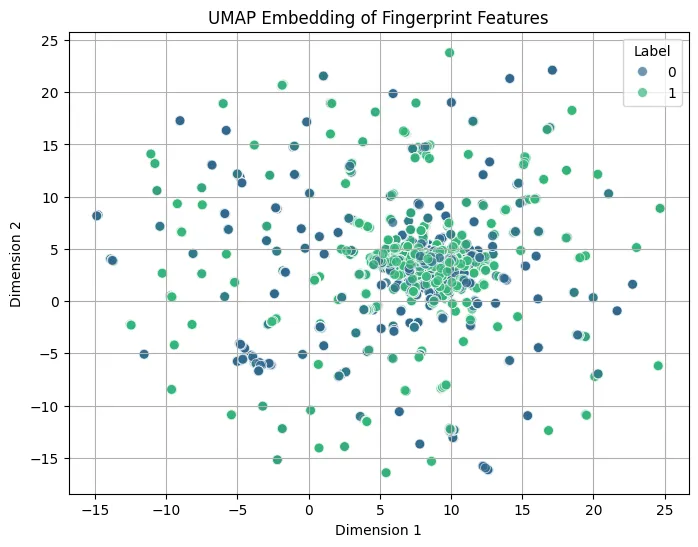
Fingerprint 데이터를 2차원으로 차원 축소
- PCA (Principal Component Analysis):
PCA모델을 생성하고, 스케일링된 Fingerprint 데이터를 2개의 주성분으로 차원 축소 .(fit_transform).- 축소된 2차원 데이터를
visualize_embedding함수를 사용하여label에 따라 색깔을 구분하여 산점도로 시각화. - 첫 번째와 두 번째 주성분이 설명하는 분산 비율을 출력하여 전체 데이터의 구조를 얼마나 잘 보존하고 있는지 확인하였다.
- t-SNE (t-distributed Stochastic Neighbor Embedding):
TSNE모델을 생성하고, 스케일링된 Fingerprint 데이터를 2차원으로 비선형 차원 축소 (fit_transform).perplexity와n_iter등의 파라미터가 설정됨.- 축소된 2차원 데이터를
visualize_embedding함수를 사용하여 시각화.
- UMAP (Uniform Manifold Approximation and Projection):
umap.UMAP모델을 생성하고, 스케일링된 Fingerprint 데이터를 2차원으로 비선형 차원 축소. (fit_transform).n_neighbors와min_dist등의 파라미터가 설정됨.- 축소된 2차원 데이터를
visualize_embedding함수를 사용하여 시각화.
결론
⇒ 뚜렷한 군집은 보이지 않음
Finger Print 종류별 UMAP 분석 결과
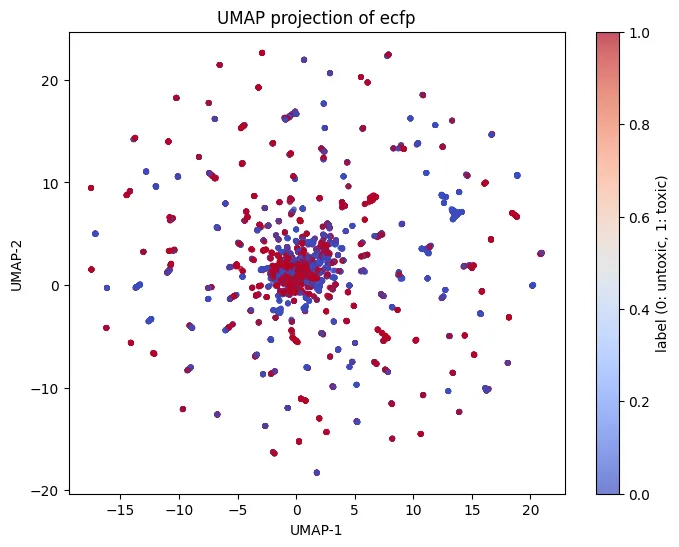
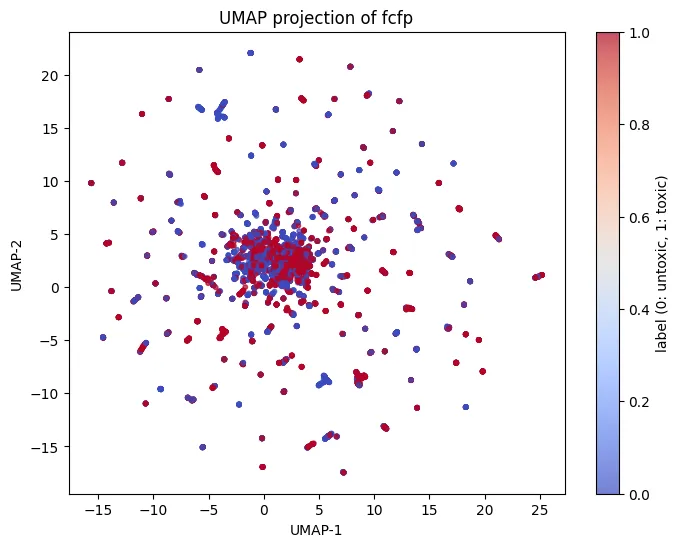
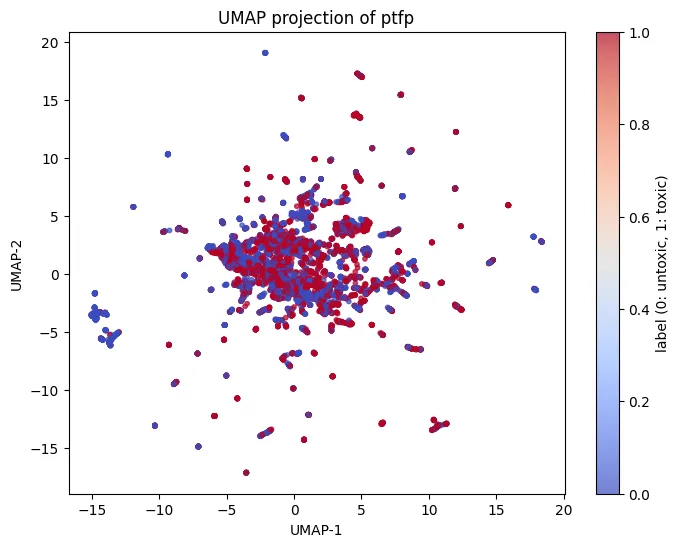
| Fingerprint 유형 | 시각적 분포 | 해석 |
|---|---|---|
| ECFP | 중앙 밀집, 색상 섞여 있음 | 독성/비독성 화합물이 혼합된 클러스터를 형성 → 구분 어려움 |
| FCFP | ECFP와 매우 유사한 패턴 | 마찬가지로 독성 여부에 따른 뚜렷한 군집 없음 |
| PTFP | 상대적으로 중앙 집중, 바깥에 분산된 소수 점들 | 약간 더 희미한 구분 가능성이 보이지만 여전히 뚜렷하지 않음 |
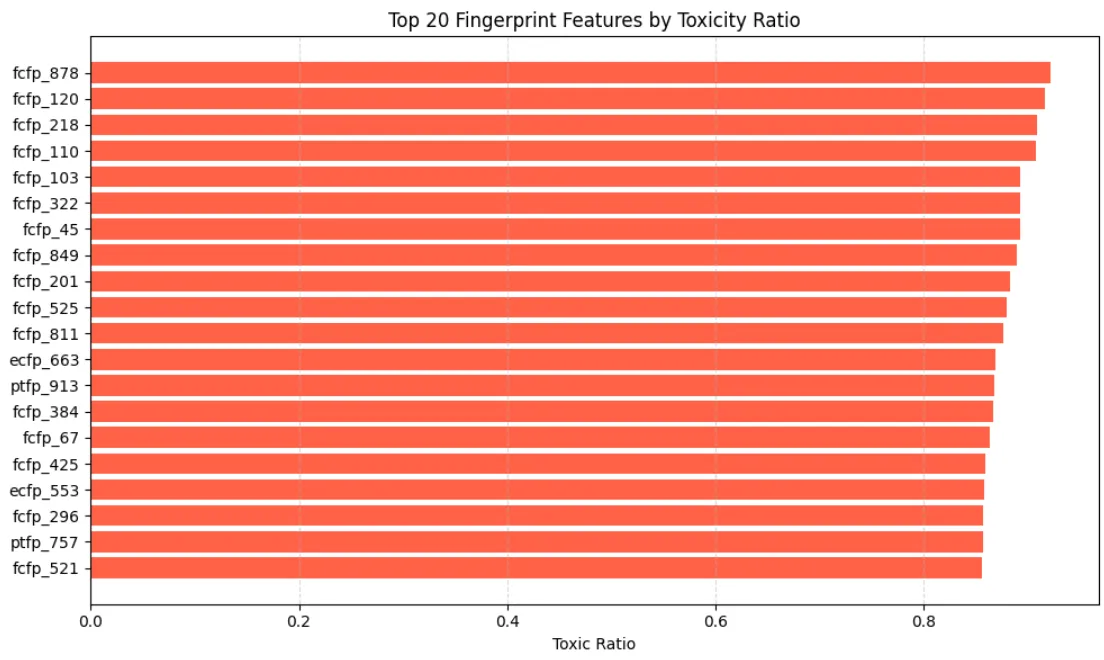
각 Fingerprint Feature에 대한 독성 비율
구조의 존재에 따른 독성 영향 하위 20
| Index | Feature | Total Count | non-Toxic Count | non-Toxic Ratio |
|---|---|---|---|---|
| 1902 | fcfp_878 | 64 | 59 | 0.9219 |
| 1144 | fcfp_120 | 12 | 11 | 0.9167 |
| 1242 | fcfp_218 | 22 | 20 | 0.9091 |
| 1134 | fcfp_110 | 195 | 177 | 0.9077 |
| 1127 | fcfp_103 | 56 | 50 | 0.8929 |
| 1346 | fcfp_322 | 223 | 199 | 0.8924 |
| 1069 | fcfp_45 | 65 | 58 | 0.8923 |
| 1873 | fcfp_849 | 36 | 32 | 0.8889 |
| 1225 | fcfp_201 | 17 | 15 | 0.8824 |
| 1549 | fcfp_525 | 108 | 95 | 0.8796 |
| 1835 | fcfp_811 | 113 | 99 | 0.8761 |
| 663 | ecfp_663 | 205 | 178 | 0.8683 |
| 2961 | ptfp_913 | 91 | 79 | 0.8681 |
| 1408 | fcfp_384 | 30 | 26 | 0.8667 |
| 1091 | fcfp_67 | 132 | 114 | 0.8636 |
| 1449 | fcfp_425 | 71 | 61 | 0.8592 |
| 553 | ecfp_553 | 211 | 181 | 0.8578 |
| 1320 | fcfp_296 | 14 | 12 | 0.8571 |
| 2805 | ptfp_757 | 28 | 24 | 0.8571 |
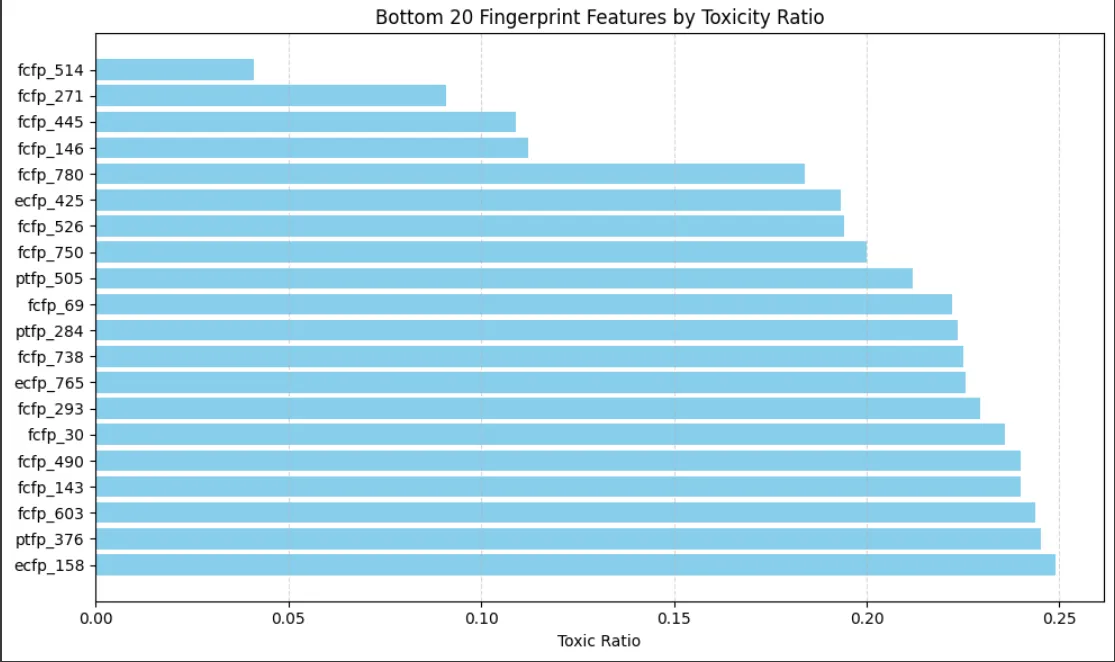
구조의 존재에 따른 독성 영향 상위 20
| Index | Feature | Total Count | non-Toxic Count | non-Toxic Ratio |
|---|---|---|---|---|
| 1538 | fcfp_514 | 73 | 3 | 0.0411 |
| 1295 | fcfp_271 | 11 | 1 | 0.0909 |
| 1469 | fcfp_445 | 275 | 30 | 0.1091 |
| 1170 | fcfp_146 | 348 | 39 | 0.1121 |
| 1804 | fcfp_780 | 87 | 16 | 0.1839 |
| 425 | ecfp_425 | 455 | 88 | 0.1934 |
| 1550 | fcfp_526 | 422 | 82 | 0.1943 |
| 1774 | fcfp_750 | 40 | 8 | 0.2000 |
| 2553 | ptfp_505 | 453 | 96 | 0.2119 |
| 1093 | fcfp_69 | 27 | 6 | 0.2222 |
| 2332 | ptfp_284 | 501 | 112 | 0.2236 |
| 1762 | fcfp_738 | 40 | 9 | 0.2250 |
| 765 | ecfp_765 | 474 | 107 | 0.2257 |
| 1317 | fcfp_293 | 109 | 25 | 0.2294 |
| 1054 | fcfp_30 | 106 | 25 | 0.2358 |
| 1514 | fcfp_490 | 450 | 108 | 0.2400 |
| 1167 | fcfp_143 | 404 | 97 | 0.2401 |
| 1627 | fcfp_603 | 41 | 10 | 0.2439 |
| 2424 | ptfp_376 | 583 | 143 | 0.2453 |
| 158 | ecfp_158 | 530 | 132 | 0.2491 |
결론
이번 분석에서는 화합물의 독성 여부와 분자 특성 간의 관계를 탐색하였다.
MolWt, clogp, sa_score, qed 네 가지 변수에 대해 KDE plot과 boxplot 등을 통해 분포를 비교하였으나, 독성 여부를 명확히 구분할 수 있는 뚜렷한 경향은 발견되지 않았다.
반면, fingerprint feature를 기준으로 분석한 결과, 특정 구조가 독성 화합물에서 매우 높은 비율로 등장하거나 거의 등장하지 않는 등, 독성과의 강한 상관성을 보이는 feature들이 다수 확인되었다.
결론적으로 수치형 특성보다는 fingerprint 기반 구조 정보가 독성 예측에 훨씬 유의미하므로, 향후 분석과 모델링은 fingerprint 중심으로 진행하는 것이 바람직하다고 판단된다.
