#5. 벡터 Indexing

- 데이터베이스에 벡터 데이터를 구조화된 인덱스에 담는 행위
- 추후 검색 성능을 고려하여 KNN이 아닌 ANN(Approximate Nearest Neighbor) 가능한 구조로 설계
목표: 검색 정확도 ↔ 검색 속도 간의 tradeoff 관계 최적화
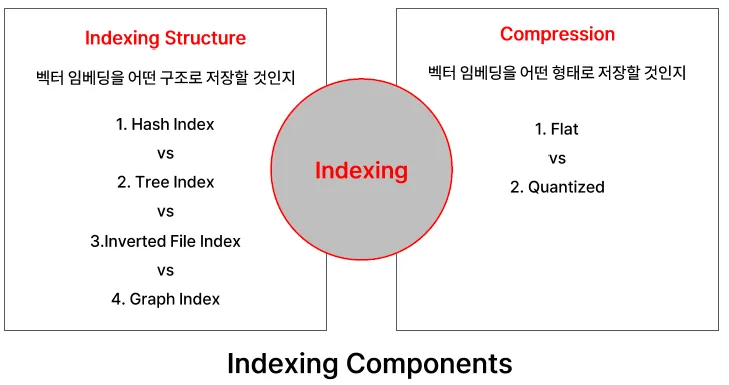
Quantinized(양자화) : 쪼개서,,,
벡터 인덱싱
벡터를 적절히 분류하고 저장하여, 유사한 벡터를 빠르게 찾음
- 예시
도서관에서 장르 별로 분류하고 원하는 장르에서 찾기
- 종류
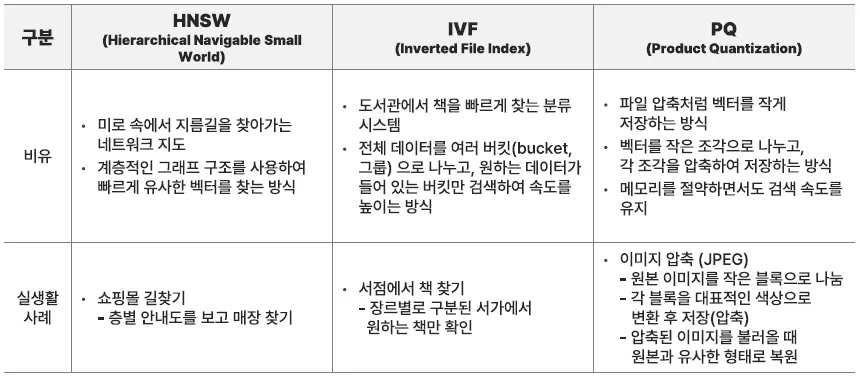
HNSW, Hierarchical Navigable Small World
최신 많이 시용하는 방법, 데이터가 수십만개 정도 되는 경우 효과적
<동작방식>
-
다층 네트워크 생성
- 벡터 데이터를 여러 계층(Layer)으로 나눔
- 상위 계층에는 적은 수의 벡터(전략적 거점)가 배치됨
- 하위 계층에는 더 많은 벡터(세부적인 노드)가 배치됨
-
빠른 검색
- 먼저 상위 계층에서 대략적인 위치를 찾음
- 하위 계층으로 내려가면서 점점 더 정확한 벡터를 탐색
- 최종적으로 가장 유사한 벡터를 반환
<장/단점>
- 장점
- 검색 속도가 매우 빠름 (로그 시간 복잡도, O(log N))
- 높은 정확도를 유지함
- 최신 벡터를 쉽게 추가할 수 있음 (동적 업데이트 가능)
- 단점
- 인덱스를 만들 때 메모리를 많이 사용
- 특정 조건에서 속도가 느려질 수 있음
근사 최근접 이웃 검색(ANN: Approximate Nearest Neighbor)을 위해 사용되며, 그래프 기반 구조와 계층적 접근 방식으로 빠른 검색 성능을 제공
IVF, Inverted File Index
여러 그룹으로 나누고 필요한 그룹에서만 검색
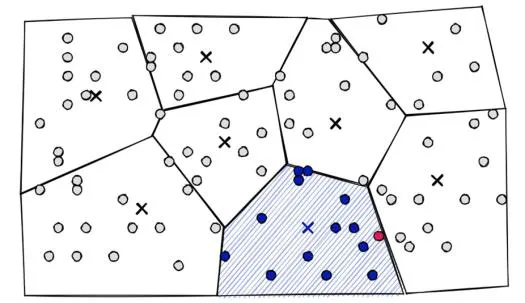
<동작방식>
-
벡터를 여러 개의 그룹(버킷)으로 분리
- K-means 알고리즘을 사용하여 유사한 벡터끼리 그룹화
- 각 그룹은 대표값(centroid, 중심점)을 가짐
-
검색 시, 가장 유사한 그룹을 먼저 찾음
- 전체 데이터를 검색하지 않고, 가장 유사한 그룹(버킷)만 탐색
- 해당 그룹 내에서 가장 가까운 벡터를 반환
-
벡터 공간을 보로노이 다이어그램과 같이 나누어 서치 스페이스를 축소
-
쿼리 벡터와 centroid 간 거리 계산 후, 가장 가까운 centroid에 해당하는 공간 내 임베딩 벡터들과 거리 계산 수행
<장/단점>
-
장점
- 전체 데이터베이스를 검색하지 않아서 속도가 빠름
- 대량의 벡터 데이터를 처리할 때 유리
- 메모리 사용량이 비교적 적음
-
단점
- 정확도가 HNSW보다 낮을 수 있음
- 그룹이 잘못 설정되면 검색 성능 저하 가능성 존재
- 새로운 벡터 추가 시 기존 그룹에 제대로 배치되지 않을 수 있음
- 공간을 형성하는 벡터가 많을수록 공간 나누는 작업의 속도가 느려짐
속도는 빠를 수 있지만, 정확도가 낮을 수 있음 ⇒ PQ와 함께 사용함
PQ, Product Quantization
벡터를 여러 개의 작은 벡터로 나누고, 각 벡터를 압축하여 저장
<동작방식>
-
벡터를 여러 개의 서브 벡터로 분리
- 예: 128차원 벡터 → 4개의 32차원 벡터로 분할
-
각 서브 벡터를 미리 정해둔 코드북(Codebook)에서 가장 가까운 값으로 매칭하여 저장
- "비슷한 벡터를 대표하는 값"을 사용하여 저장 공간 절감
-
검색 시, 압축된 값만 비교하여 빠르게 유사도를 계산
- 원본 벡터를 모두 비교하는 것보다 훨씬 빠름
코드북(Codebook)은 서브 벡터들을 대표하는 기준 벡터(클러스터 중심)들의 집합으로, 유사한 벡터를 압축하여 표현할 때 참조되는 값들
<장/단점>
-
장점
- 벡터를 압축해서 저장하므로 메모리 사용량이 적음
- 대규모 데이터에서도 유사도 검색을 빠르게 수행 가능
-
단점
- 벡터를 압축하는 과정에서 정확도가 조금 떨어질 수 있음
- 너무 작은 차원으로 압축 시 원본 데이터의 특성을 잃을 수 있음
메모리 사용량이 적은 편이라 대규모 데이터에 적합함
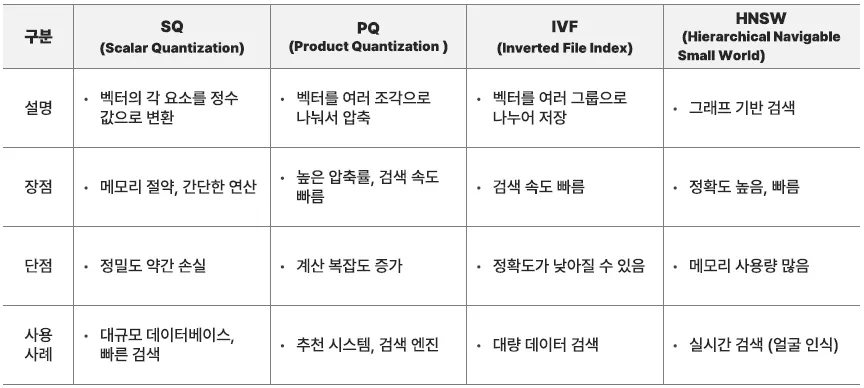
HNSW, IVF, PQ 개념 요약
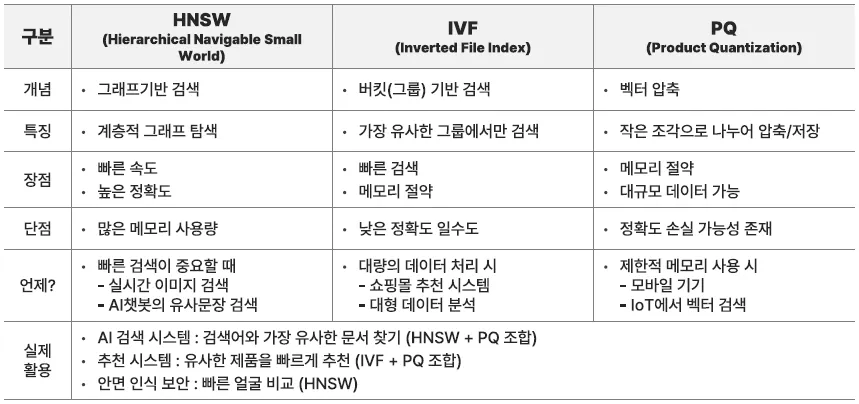
⇒ 하나만 고집해서 사용하는 것이 아닌, 여러 방법을 섞어서 사용
Hash Index
고차원 데이터는 그대로 두는데, 해시 테이블을 별도로 만들어서
<동작방식>
-
고차원 데이터를 저차원 해시코드로 변환하여 서칭 컴플렉시티 개선을 노리는 방식
-
일반적 해싱과 반대로, 벡터 인덱싱 시 비슷한 데이터끼리 해시 충돌이 나도록 하는 구조
-
이때 사용되는 해싱 함수를 그대로 쿼리 벡터에 대해서도 적용시켜, 동일한 해시버킷에 위치한 벡터들에 대해서만 거리 계산 수행
-
LSH(Locally Sensitive Hashing) 등이 여기에 해당
<장/단점>
- 장점
- 빠른 검색 속도
- 단점
- 낮은 검색 정확도
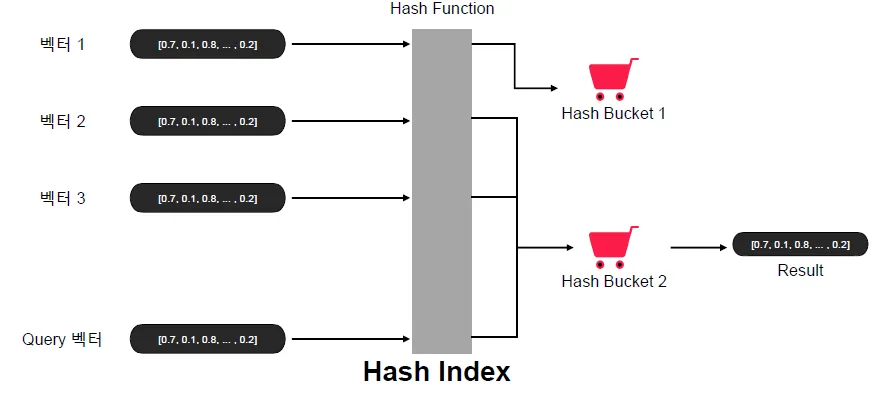
Query가 들어오면 Hash Index화 하고 유사함 Bucket으로 가서 유사한 Hash 값을 찾음
Tree Index
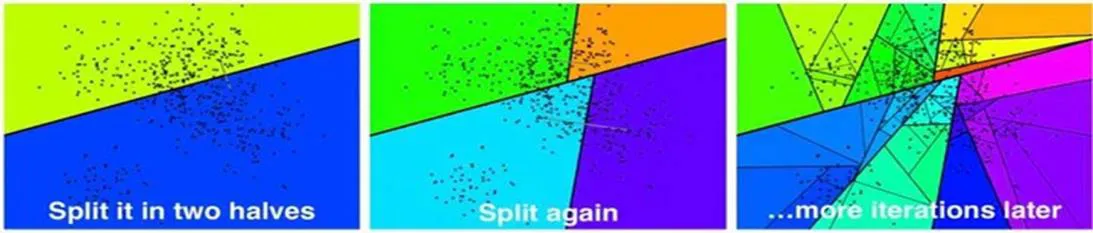
<동작방식>
-
Binary Search Tree 구조를 사용하여 고차원 벡터 공간에서의 검색 속도 향상을 도모하는 방식
-
유사한 벡터들이 같은 서브트리 노드(혹은 공간)에 속하도록 하는 구조
-
검색 시, 해시버킷과 유사하게 쿼링 벡터가 속하는 서브트리 노드에 존재하는 다른 벡터들과의 거리만 계산하여 검색 속도 최적화
-
Spotify Annoy 알고리즘이 여기에 해당
<장/단점>
- 장점
- 빠른 검색 속도
- 단점
- 고차원 벡터에 대해서는 검색 정확도가 좋지 않다
-
HNSW: 그래프를 따라 돌아다니며 "지금보다 더 가까운 이웃은 없을까?"를 반복적으로 묻는 방식
-
Tree Index: "이쪽 리프 노드면 이 근처에 있을 거야"라고 트리를 타고 내려가는 방식
| 항목 | HNSW | Tree Index (Annoy, KD-Tree 등) |
|---|---|---|
| 기본 구조 | 계층적 그래프 구조 (Small World Graph) | 트리 구조 (Binary Tree, KD-Tree, Ball Tree 등) |
| 탐색 방식 | 상위 계층에서 시작해 하위로 내려가며 점점 더 정확한 이웃을 탐색 | 트리의 리프 노드까지 탐색하여 근접한 후보 벡터 추출 |
| 정확도 | 매우 높음 (거의 정확 검색 수준에 근접) | 비교적 낮음 (특히 고차원에서는 성능 급감) |
| 검색 속도 | 빠름 (로그 시간 복잡도 O(log N)) | 빠름 (단, 차원 증가 시 느려질 수 있음 → "차원의 저주") |
| 메모리 사용량 | 높음 (그래프 전체를 메모리에 유지해야 함) | 낮거나 중간 수준 (구현 방식에 따라 다름) |
| 구축 시간 | 상대적으로 오래 걸림 | 빠르거나 중간 수준 |
| 동적 업데이트 | 가능 (벡터 삽입/삭제 지원) | 대부분 불가능 또는 재구축 필요 (정적 인덱스가 많음) |
| 고차원 데이터 적합성 | 매우 적합 (그래프 기반이 고차원에서도 잘 동작) | 부적합 (고차원에서는 트리 구조 성능 급격히 하락) |
| 사용 예 | hnswlib, Faiss IndexHNSW | Spotify Annoy, scikit-learn KDTree/BallTree, Faiss IndexFlatTree |
Graph Index
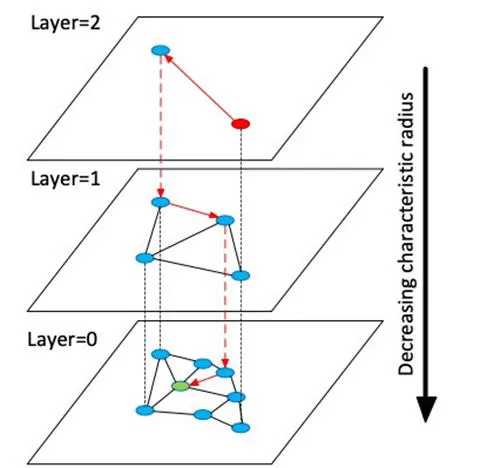
HNSW가 대표적임
<동작방식>
-
임베딩 벡터들을 그래프 구조로 구성하여, 임베딩 벡터를 노드로, 연결된 엣지를 벡터 간 거리로 표현
-
유사한 벡터끼리 엣지 커넥션이 더 잘 이루어지도록 설계
-
HNSW(Hierarchical Navigable Small World) 알고리즘이 여기에 해당
-
여러 계층으로 그래프를 제작
- 가장 밀도가 낮은 계층에서 랜덤한 노드로 시작하여, 해당 계층에서 가장 가까운 노드를 찾은 후 다음 계층으로 이동
- 최종적으로 원래 쿼리 벡터와 가장 가까운 이웃을 찾을 때까지 계층 탐색
<장/단점>
- 장점
- 검색 속도도 빠르고 검색 성능도 빠르다
- 단점
- 검색 그래프를 구성하는 방식에 따라 검색 성능이 의존적 (파라미터 튜닝 필요)
Flat Indexing(Exhaustive Search)
모든 데이터를 하나하나 비교하는 방식
<동작방식>
-
모든 데이터를 하나하나 비교하는 방식
-
벡터를 압축 없이 그대로 저장
-
검색할 때 모든 벡터를 하나씩 비교 (완전 탐색, brute-force search)
-
정확도가 높지만 속도가 느리고, 메모리를 많이 사용
-
사용 사례
- 데이터 개수가 적거나, 정확도가 중요한 경우
- 의료 데이터 분석 (잘못된 결과가 나오면 안 되는 경우)
- 소규모 데이터에서 가장 가까운 벡터를 찾을 때
<장/단점>
- 장점
- 100% 정확한 검색 결과 (손실 없음)
- 추가적인 전처리 없이 사용 가능
- 단점
- 데이터가 많아질수록 속도가 느려짐
- 메모리 사용량이 많음
Quantized 인덱싱, 양자화 방식
벡터를 압축하여 저장하고, 근사 검색을 수행하는 방식
- 양자화
벡터를 압축하여 더 적은 공간을 사용하고 검색 속도를 빠르게 하는 기법
| 방법 | 방식 설명 | 특징 | 활용 사례 |
|---|---|---|---|
| PQ(Product Quantization, 제품 양자화) | 벡터를 여러 작은 부분(서브벡터)으로 나눈 후 각각을 압축하여 저장 | 메모리를 크게 줄이면서도 높은 성능 유지 | 대규모 데이터에서 유사 이미지 검색 |
| IVF(Inverted File Index + Quantization) | 데이터를 여러 그룹으로 나눈 후, 가까운 그룹에서만 검색 | 검색 속도는 빨라지지만 정확도가 약간 떨어질 수 있음 | 쇼핑몰 추천 시스템, 검색 엔진 |
| LSH(Locality-Sensitive Hashing) | 비슷한 벡터끼리 같은 해시값을 부여하여 검색 속도를 높임 | 대규모 데이터에서 근사 검색할 때 유용 | 음성 인식, 근사 검색 |
<장점>
-
검색 속도가 빠름
-
메모리 사용량 절약 가능
<단점>
- 완벽한 검색이 아닌 근사 검색(Approximate Search) → 정확도가 약간 낮을 수 있음
<사용 사례>
- 데이터가 많고 빠른 검색이 필요한 경우
- 예) 수억 개의 상품 중 유사한 것을 추천하는 쇼핑몰 추천 시스템
- 예) 실시간 검색 시스템 (구글 이미지 검색, 영상 검색 등)
정확도를 중요시 하면 Flat, 속도를 중요시 하면 Quantized
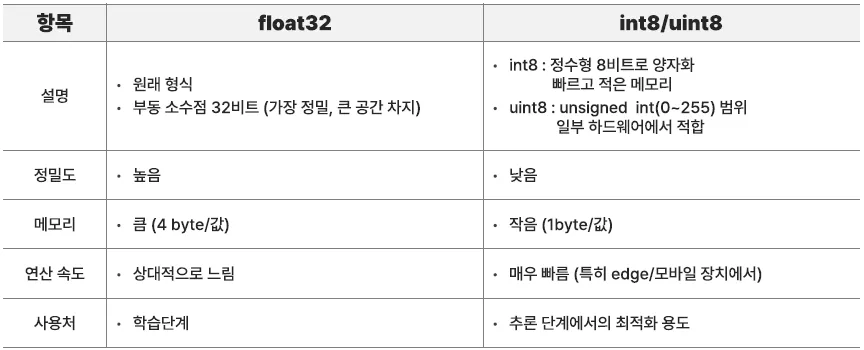
Scalar Quantization, SQ
벡터 인덱싱에서 벡터를 더 작은 크기로 변환하여 저장하는 기법
→ 벡터의 각 요소를 특정 범위의 정수값으로 변환(압축)하여 메모리를 절약하는 방법


| 사용 목적 | SQ 사용 여부 및 이유 |
|---|---|
| 정확도가 중요할 때 | No❌ (SQ는 근사 검색 방식이므로 부적합) |
| 대규모 벡터 데이터베이스 | Yes ⭕ (메모리 절약 효과 있음) |
| 빠른 검색이 필요할 때 | Yes ⭕ (저장 공간이 작아져 연산 속도 향상) |
| 딥러닝 모델 경량화 | Yes ⭕ (모델 크기 감소 효과 있음) |
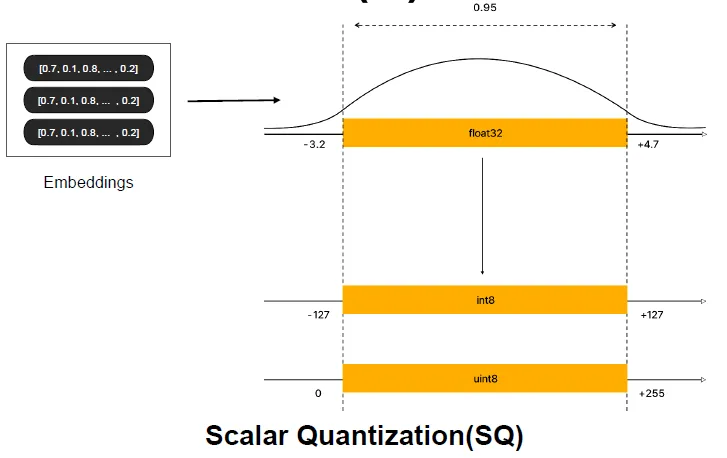
-
모바일, 임베디드, Edge AI 환경에서 속도와 저장 공간을 최적화하기 위함
-
특히 int8은 양자화된 모델을 실행할 수 있는 TensorRT, ONNX Runtime, TFLite 등에서 활발히 사용
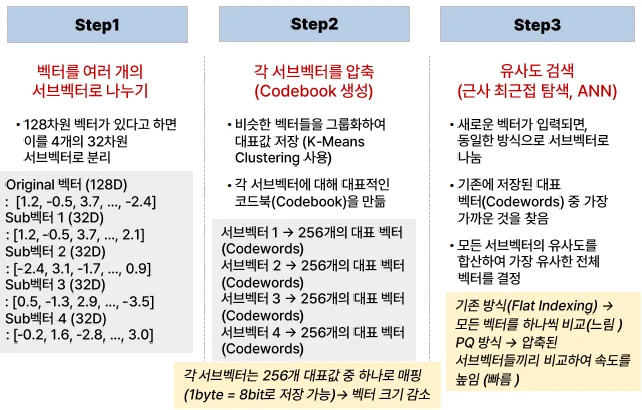
Product Quantization, PQ
대규모 벡터 데이터의 검색 속도를 높이고 메모리를 절약하는 인덱싱 기법
벡터 압축 후 근사 검색 수행
장점
-
메모리 절약 → 벡터를 압축하여 저장 가능
-
검색 속도 향상 → 근사 검색을 통해 빠르게 유사한 벡터 탐색
-
대규모 데이터에 적합 → 수억 개의 벡터도 효율적으로 저장 및 검색 가능
단점
-
정확도가 완전 탐색(Flat Indexing)보다 약간 낮음
-
적절한 코드북(Codebook) 크기 설정이 필요
-
고차원 벡터에서는 압축 과정이 복잡할 수 있음
언제 사용?
-
대규모 데이터에서 빠른 검색이 필요할 때
-
메모리를 절약하면서 유사 검색을 수행할 때
-
추천 시스템, 이미지 검색, 문서 검색 등에 활용
대표 활용 예
-
Google 이미지 검색
-
Netflix 추천 시스템
-
시기반 챗봇 검색 시스템
-
FAISS (Facebook AI Similarity Search)
요약
Product Quantization(PQ)는 대규모 데이터에서 메모리를 절약하고 빠르게 검색할 때 사용된다. 정확도가 약간 떨어질 수 있지만, 속도와 효율성을 크게 향상시킨다.
<정리>
-
Scalar Quantization 기법과 유사하게, 임베딩 벡터의 floating point 값을 8비트 integer로 변환하여 메모리 효율성을 높이는 기법
-
이 방식에 몇 가지 추가 기술이 결합된 것이 바로 PQ (Product Quantization)
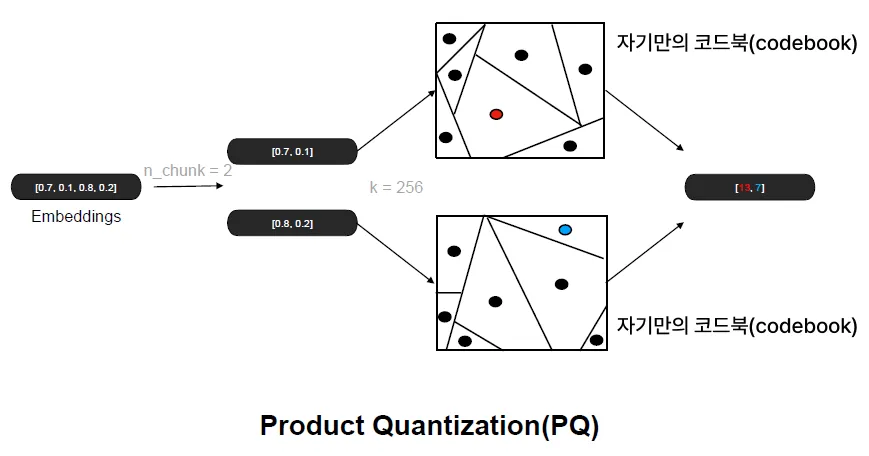
-
원본 벡터를 n개의 청크 또는 서브벡터 단위로 분할
-
각 서브벡터 단위로 K-means 클러스터링을 수행 (예: K = 256)
-
클러스터링 결과로 얻은 256개의 centroid를 서브벡터의 표현으로 사용하여 양자화(Quantization) 수행
-
새로운 쿼리 벡터가 들어오면 동일한 방식으로 서브벡터 단위로 나누고, 각 서브벡터별로 해당 centroid에 매핑하여 8비트 정수 형태로 변환
-
이후 거리 계산 시, 메모리 효율성과 검색 속도 모두 향상되는 방식
-
덜 쪼갤수록 압축률은 올라가지만 정확도가 낮아지고, 더 많이 쪼개면 정확도는 올라가지만 압축률은 낮아지는 trade-off 관계 존재
import faiss
import numpy as np
# 1. 1000개의 128차원 벡터 생성 (더미 데이터)
d = 128 # 벡터 차원
nb = 1000 # 데이터베이스 크기
np.random.seed(42)
data = np.random.random((nb, d)).astype('float32')
# 2. Product Quantization (PQ) 인덱스 생성
m = 8 # 서브벡터 개수
quantizer = faiss.IndexFlatL2(d) # 기본 L2 거리 기반
index = faiss.IndexIVFPQ(quantizer, d, 10, m, 8) # IVF + PQ 적용
index.train(data) # 학습
index.add(data) # 벡터 추가
# 3. 검색 수행
query = np.random.random((1, d)).astype('float32')
D, I = index.search(query, k=5) # 가장 가까운 5개 검색
print("검색 결과 (Nearest Neighbors):", I)
print("거리 (Distances):", D)| 항목 | 설명 |
|---|---|
| Method | 인덱싱 알고리즘 설명 |
| Class name | 사용되는 FAISS 클래스 이름 |
| index_factory | faiss.index_factory()에서 문자열로 지정되는 인덱스명 |
| Main parameters | 인덱스 생성 시 필요한 주요 파라미터 (예: 벡터 차원 수 d, 클러스터 수 등) |
| Bytes/vector | 각 벡터가 차지하는 메모리 바이트 수 |
| Exhaustive | 전체 검색 여부 (예: 정확도 100% 여부) |
FAISS를 사용하면 쉽게 Product Quantization을 적용가능
