벡터 DB (5) - 유사도 측정

이영진·2025년 5월 8일
LLMSKALAVectorDB생성형 ai
1

LLM

목록 보기
17/25

두 데이터 간의 유사성을 평가하는 방법

  • 머신러닝, 정보 검색, 자연어 처리 등 다양한 분야에서 활용
  • 데이터 간의 관계를 수치화할 때 유용

코사인 유사도, cosine similarity

두 벡터 사이의 각도를 기준으로 유사도를 측정하는 방식.

→ 두 벡터가 이루는 각도가 작을수록(즉, 방향이 비슷할수록) 유사도가 높음.

수식:

공식

CosineSimilarity=A⋅B∥A∥×∥B∥Cosine Similarity= \frac{A \cdot B}{\|A\| \times \|B\|}
A⋅BA⋅B

두 벡터의 내적

∥A∥,∥B∥∥A∥,∥B∥

각 벡터의 크기 (Euclidean norm)

<예제>

  • A = [1, 2, 3], B = [2, 3, 4] 라는 두 벡터가 주어졌을 때
  1. 내적 계산
A⋅B=(1×2)+(2×3)+(3×4)=2+6+12=20A⋅B=(1×2)+(2×3)+(3×4)=2+6+12=20
  1. 벡터 크기 계산
∥A∥=12+22+32=14,∥B∥=22+32+42=29\|A\| = \sqrt{1^2 + 2^2 + 3^2} = \sqrt{14}, \quad \|B\| = \sqrt{2^2 + 3^2 + 4^2} = \sqrt{29}
  1. Cosine Similarity 계산
Cosine Similarity=2014×29≈0.99\text{Cosine Similarity} = \frac{20}{\sqrt{14} \times \sqrt{29}} \approx 0.99

→ 1에 가까울수록 유사한 벡터임을 의미

<활용 분야>

  • 문서 간 유사도 비교 (예: 뉴스 기사 추천)
  • 추천 시스템 (예: 영화 추천)
  • 검색 엔진 (예: 사용자 검색어와 문서 간 유사도 평가)

유클리드 거리

두 점(벡터) 사이의 직선 거리를 측정하는 방법으로, 쉽게 말해 두 점이 얼마나 떨어져 있는지를 표시

Euclidean Distance=(x1−x2)2+(y1−y2)2+…\text{Euclidean Distance} = \sqrt{(x_1 - x_2)^2 + (y_1 - y_2)^2 + \ldots}
  • 각 차원의 차이를 제곱하여 더한 후, 제곱근을 구함

<예제>

  • 두 개의 점 A와 B 사이의 유클리드 거리 A(1,2) 와 B(4,6)
  • 각 차원의 계산
(4−1)2=9,(6−2)2=16(4-1)^2 = 9, (6-2)^2 = 16
  • 합산 후 제곱근 계산
9+16=25=5\sqrt{9 + 16} = \sqrt{25} = 5

→ 두 점 사이의 거리는 5

<활용 예>

  • 이미지 검색: 색상이나 패턴이 유사한 이미지 찾기
  • 클러스터링: K-means 알고리즘에서 데이터를 군집화할 때
  • 추천 시스템: 사용자와 아이템 간의 거리 측정

기타 유사도 측정 방법

자카드 유사도 (Jaccard Similarity)

  • 집합(Set) 간의 유사도를 비교하는 방법
  • 교집합과 합집합의 비율을 사용
Jaccard Similarity=∣A∩B∣∣A∪B∣\text{Jaccard Similarity} = \frac{|A \cap B|}{|A \cup B|}
  • 예시: A = {사과, 바나나, 오렌지} B = {바나나, 오렌지, 수박}
    →유사도=24=0.5→ 유사도 = \frac{2}{4} = 0.5
  • 활용 분야:
    • 텍스트 중복 탐지
    • 사용자 취향 비교

마할라노비스 거리 (Mahalanobis Distance)

  • 데이터의 분산과 공분산을 고려한 거리 측정 방식
  • 데이터가 서로 다른 분포를 가질 때, 유클리드 거리보다 더 신뢰할 수 있는 방식
DM(A,B)=(A−B)TS−1(A−B)D_M(A, B) = \sqrt{(A - B)^T S^{-1} (A - B)}
  • 여기서
S−1S^{-1}

은 공분산 행렬의 역행렬

  • 활용 분야:
    • 이상치 탐지
    • 다변량 데이터 분석

내적 유사도 (Dot Product Similarity)

  • 두 벡터의 내적(Dot Product)을 계산하여 유사도를 측정하는 방법
A⋅B=x1y1+x2y2+⋯+xnynA \cdot B = x_1 y_1 + x_2 y_2 + \cdots + x_n y_n
  • 내적 값이 클수록 두 벡터가 비슷한 방향을 가짐을 의미
  • 활용 예시
    • 신경망 가중치 적용 (딥러닝)
    • 추천 시스템 (사용자 선호도 예측)

맨해튼 거리 (Manhattan Distance)

  • 각 차원의 차이의 절댓값을 더해서 거리를 측정하는 방식
  • “격자 무늬 거리”라고도 하며, 도시 블록처럼 수직·수평 방향으로만 이동하는 거리 방식과 유사
Manhattan Distance=∣x1−x2∣+∣y1−y2∣+⋯\text{Manhattan Distance} = |x_1 - x_2| + |y_1 - y_2| + \cdots
  • 예시: A(1,2) 와 B(4,6)의 맨해튼 거리
    ∣4−1∣+∣6−2∣=3+4=7|4 - 1| + |6 - 2| = 3 + 4 = 7
  • 활용 예시
    • 네트워크 라우팅 (최적 경로 찾기)
    • 주식 데이터 비교 (가격 변화량 분석)

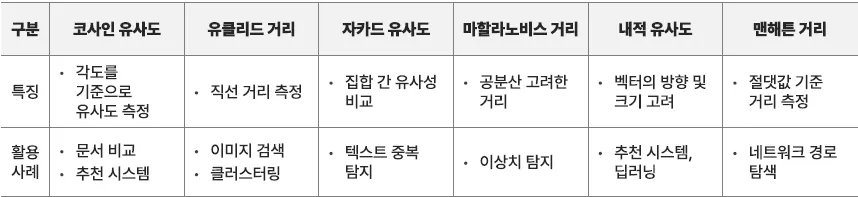
유사도 측정 방식은 상황에 따라 다르게 적용되니 데이터의 특징과 목적에 따라 적절한 방식 선택

공분산 행렬, Covariance Matrix

  • 여러 변수 간의 공분산(Covariance) 값을 정리한 행렬
  • 공분산은 두 변수 간의 관계를 나타내는 값
    • 양수: 양의 상관관계 (함께 증가)
    • 음수: 음의 상관관계 (한쪽 증가, 한쪽 감소)
    • 0: 관계 없음
  • 데이터의 분포 특성을 분석할 때 사용
  • 활용 분야:
    • PCA(주성분 분석)
    • 머신러닝
    • 통계분석
    • 금융공학 등

<정의 및 계산식>

  • 두 변수 XX 와 YY 의 공분산:
Cov(X,Y)=1n∑i=1n(Xi−Xˉ)(Yi−Yˉ)\text{Cov}(X, Y) = \frac{1}{n} \sum_{i=1}^{n} (X_i - \bar{X})(Y_i - \bar{Y})
  • 설명:
    • n: 데이터 개수
    • X_i, Y_i: 각 X와 Y 변수의 값
    • 각 X와 Y의 평균
  • 의미:
    • X 증가, Y 증가 → 공분산 > 0 (양의 상관관계)
    • X 증가, Y 감소 → 공분산 < 0 (음의 상관관계)
    • X와 Y가 서로 관계 없음 → 공분산 = 0

【활용】

  • PCA (주성분 분석)
    • 공분산 행렬을 사용하여 데이터의 주요 방향(주성분)을 찾고 차원 축소 수행
  • 다변량 정규분포 분석
    • 여러 개의 변수가 동시에 정규분포를 따를 때, 그 관계를 나타내는 데 사용
  • 포트폴리오 최적화 (금융공학)
    • 주식 간의 변동성을 분석하여 리스크를 최소화하는 투자 포트폴리오 구성
  • 머신러닝 및 데이터 분석
    • 데이터의 상관관계를 분석하고, 변수 선택(feature selection)에 활용

【Python 활용 예제】

  • Python에서는 numpy 라이브러리를 이용하여 쉽게 공분산 행렬 계산 가능
import numpy as np

# 예제 데이터: 3개의 변수 (X, Y, Z)
data = np.array([
    [1, 2, 3],
    [2, 3, 5],
    [3, 4, 6],
    [4, 5, 6]
])

# 공분산 행렬 계산
cov_matrix = np.cov(data, rowvar=False)

print("공분산 행렬:\n", cov_matrix)
  • 결과:
공분산 행렬:
[[1.66 1.66 0.5 ]
 [1.66 1.66 1.0 ]
 [0.5  1.0  2.66]]
  • 설명
    • 대각선: 각 변수의 분산
    • 나머지 값: 변수 간의 공분산
구분공분산 행렬상관 행렬
값의 범위-∞ ~ +∞-1 ~ +1
크기 영향원래 데이터 크기에 따라 다름크기와 단위에 영향을 받지 않음
계산 방식공분산 값을 그대로 사용공분산을 표준화(정규화)한 값 사용
활용데이터의 분포와 관계 파악변수 간의 강한/약한 상관관계 분석
profile
이영진
이전 포스트

벡터 DB (4) - 벡터 Indexing

다음 포스트

벡터 DB (6) - 근사 최근접 이웃 (ANN) 검색

0개의 댓글