벡터 DB (6) - 근사 최근접 이웃 (ANN) 검색

이영진·2025년 5월 8일

LLM SKALA VectorDB 생성형 ai

LLM

목록 보기

18/25

#7. 근사 최근접 이웃 (ANN) 검색

ANN이란 질문 벡터(Query 벡터)에 대해 가장 비슷한 데티어(Nearest Neighbor)를 찾는 작업

정확도는 조금 낮아져도, 속도를 크게 높이는 것이 목표!!

VDB 검색 알고리즘

■ VDB

고차원 벡터 데이터를 저장
벡터 간의 유사성 검색을 효율적으로 수행하는 시스템

■ VDB 중요성

이미지 검색, 자연어 처리, 추천 시스템 등 대규모 벡터 데이터를 다루는 경우 검색 속도는 시스템의 성능과 사용자 경험에 매우 중요

KNN (K-Nearest Neighbor) 알고리즘

정의

KNN(K-Nearest Neighbor, K-최근접 이웃) 알고리즘은 머신러닝과 검색 시스템에서 가장 기본적인 알고리즘 중 하나

【 KNN이란? 】

단순하지만 강력한 분류(Classification) 및 회귀(Regression) 알고리즘
새로운 데이터 포인트(예측할 데이터)가 들어오면,
- 주변에 있는 K개의 가장 가까운 데이터를 찾아서
- 다수결(분류) 또는 평균(회귀)을 통해 예측
비슷한 친구가 많으면 나도 그 부류에 속할 가능성이 높다는 개념

“비슷한 데이터는 비슷한 특성을 가진다”는 아이디어에서 출발

<장/단점>

장점	단점
이해하기 쉽고 구현이 간단	데이터가 많아질수록 속도가 느려짐
선형적(직선 형태) 관계가 아닌 복잡한 패턴도 잘 찾음	차원이 높아지면 거리 계산이 어려워짐 (고차원 문제)
특정한 학습 과정이 필요 없음 (즉시 예측 가능)	메모리 사용량이 큼 (모든 데이터를 저장해야 함)

보통 K는 홀수로 설정하여 다수결 판별이 용이하도록 함.

주요 내용

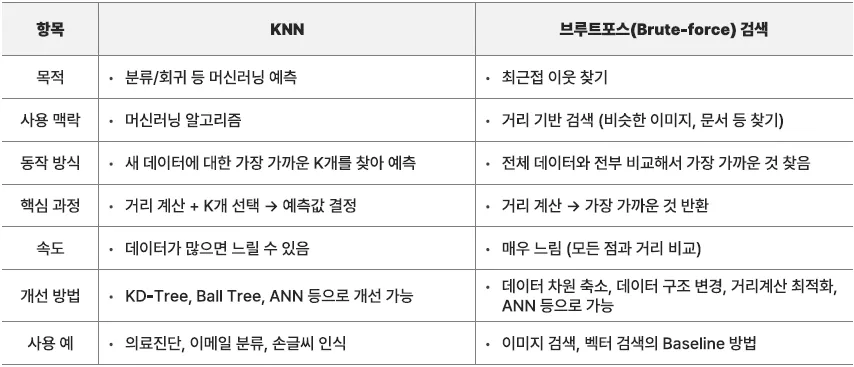
브루트포스 검색(유사한 데이터 찾는 데 집중) 대비 KNN은 예측을 목표
KNN에서 거리 계산을 하기 위해 브루트포스, KD-Tree, Ball Tree, ANN(HNSW 등) 사용 가능
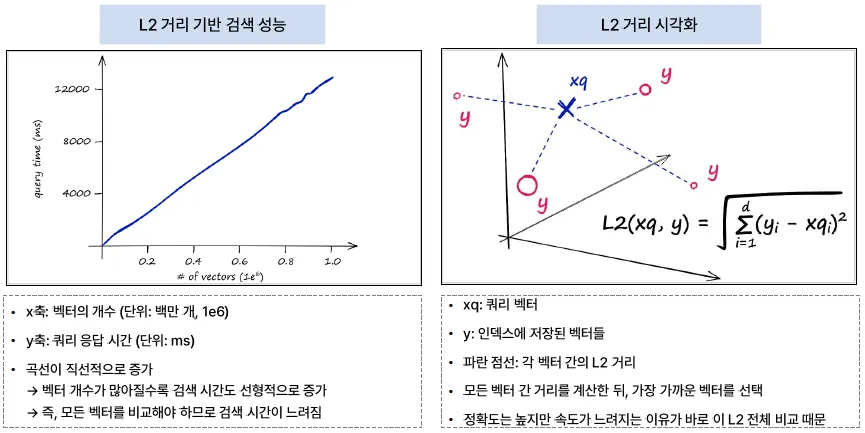
쿼리 벡터와 전체 벡터를 거리(L2, Cos 등)로 직접 비교하여 유사한 것 탐색
- 검색을 위한 쿼리 벡터 검색 시 모든 벡터와 직접 비교 (L2, Cos, Dot-product)
가장 정확한 검색 방법
데이터 개수가 많아지면 검색 시간이 데이터 개수에 따라 증가

KNN을 활용하여 간단한 분류

from sklearn.neighbors import KNeighborsClassifier
import numpy as np

# 간단한 데이터: [키(cm), 몸무게(kg)]
X = np.array([[180, 80], [160, 50], [170, 60], [155, 45], [190, 90]])

# 정답(라벨)
y = np.array(["남자", "여자", "남자", "여자", "남자"])

# KNN 모델 생성 (K=3)
knn = KNeighborsClassifier(n_neighbors=3)
knn.fit(X, y)

# 새로운 사람 [165cm, 55kg]이 남자인지 여자인지 예측
new_person = np.array([[165, 55]])
prediction = knn.predict(new_person)

print("예측 결과:", prediction)  # 출력: ['여자']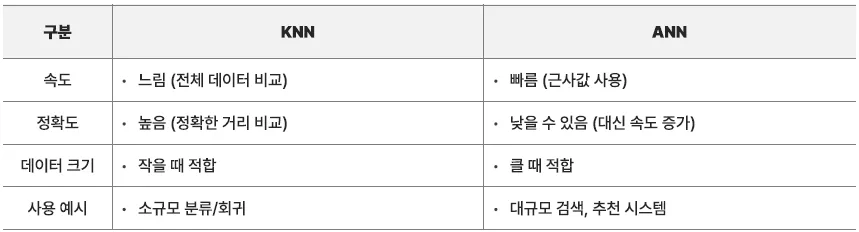

ANN은 근사값을 사용해서 속도를 빠르게 하는 KNN의 개선 버전

브루트포스 검색

가능한 모든 경우를 전부 탐색하여 해답을 찾는 방식

import numpy as np
from sklearn.metrics.pairwise import euclidean_distances

# 쿼리 벡터 (예: [3, 3])
query = np.array([[3, 3]])

# 데이터셋 (비교 대상 벡터들)
data = np.array([[1, 1], [2, 2], [5, 5], [6, 6]])

# 거리 계산
distances = euclidean_distances(query, data)
print("거리:", distances)

# 가장 가까운 2개 인덱스 추출
nearest_index = np.argsort(distances[0])[:2]
print("가장 가까운 2개:", data[nearest_index])

시간이 매우 오래 걸리므로 GPU를 사용하여 병렬처리함

브루트포스 검색 – Search on GPU (Flat: 브루트포스)

개요

모든 임베딩 벡터를 GPU의 VRAM에 업로드한 후 검색 수행
브루트포스 방식이지만 GPU를 사용하면 매우 빠른 응답 속도 제공
VRAM 용량에 따라 처리 가능한 벡터 수가 결정됨

◾ 단일 GPU 사용

res = faiss.StandardGpuResources()                 # GPU 자원 할당
index_flat = faiss.IndexFlatL2(d)                  # L2 거리 기반 Flat Index 생성

gpu_index_flat = faiss.index_cpu_to_gpu(res, 0, index_flat)  # GPU로 인덱스 이동
gpu_index_flat.add(xb)                             # 임베딩 벡터 추가
D, I = index.search(xq, k)                         # 검색 수행

◾ 멀티 GPU 사용

cpu_index = faiss.IndexFlatL2(d)                            # CPU 상의 인덱스 생성
gpu_index_flat = faiss.index_cpu_to_all_gpus(cpu_index)     # 모든 GPU로 인덱스 복사
gpu_index_flat.add(xb)                                      # 임베딩 벡터 추가
D, I = index.search(xq, k)                                  # 검색 수행

ANN 알고리즘

ANN 알고리즘 (Approximate Nearest Neighbor)

정의: 대규모 벡터 데이터셋에서 특정 벡터와 가장 유사한 벡터를 빠르게 찾기 위한 검색 기법
특징:
- KNN과 비교 시 정확도를 약간 희생하는 대신 검색 속도 향상
- 고차원 벡터 공간에서 근사값을 빠르게 계산해 유사한 결과 반환

주요 ANN 알고리즘

알고리즘	설명
LSH (Locality Sensitive Hashing)	해시 함수를 통해 유사한 벡터가 동일한 해시 버킷에 위치하도록 설계
IVF (Inverted File Index)	벡터를 클러스터로 나눈 후, 각 클러스터 내에서 세부 검색 수행
PQ (Product Quantization)	벡터를 여러 하위 벡터로 분할 후, 양자화하여 압축 검색
HNSW (Hierarchical Navigable Small World)	그래프 기반 알고리즘으로 고차원에서도 정확도와 검색 속도를 모두 확보 가능

LSH, Locality Sensitive Hashing

구분	내용
구조	해시테이블 기반
원리	- 비슷한 데이터는 같은 해시 버킷에 들어가도록 설계 - 질의 벡터가 들어오면 같은 해시 버킷만 조회하여 전체 비교를 피함
장점	- 계산 속도가 빠름
단점	- 차원이 높아질수록 성능 저하 발생 - 정확도는 다소 낮은 편
사용 예시	텍스트 유사도 검색, 대규모 로그 데이터 분석

LSH의 구조

구성 요소	설명
Keys	입력 벡터들 (예: 문서 임베딩, 이미지 벡터 등)
Hashing Function	각 벡터에 해시 함수를 적용하여 특정 해시 값으로 변환
Hash Buckets	해시 값이 같은 벡터들은 동일한 버킷에 저장됨 → 유사한 벡터들이 같은 버킷에 위치하도록 해시 함수 설계
Values (우측)	각 버킷 내 값들만 대상으로 최근접 탐색 (Nearest Neighbor Search) 수행

LSH의 장점

전체 벡터를 비교하지 않아 속도가 빠름
해시 버킷을 기준으로 검색 대상이 자동으로 줄어듦

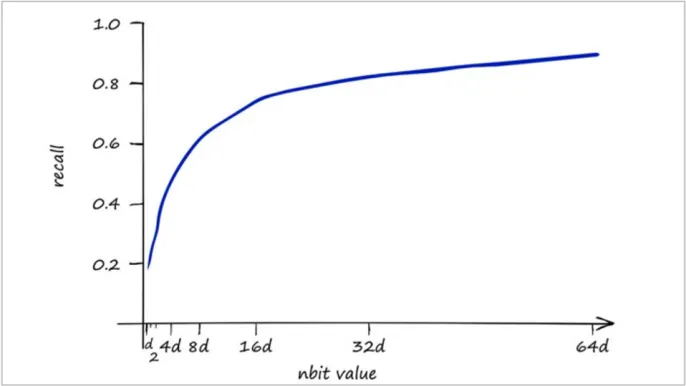
해시 비트 수(nbit) vs Recall

항목	설명
nbit	해싱 비트 수 (해시 표현의 정밀도, x축)
recall	검색 정확도 (실제 가장 유사한 벡터를 잘 찾았는지, y축)

관계 및 특징

nbit가 작을수록: recall이 낮아짐 (정확도 떨어짐)
nbit가 커질수록: recall이 높아짐 (정확도 향상)
그러나 32bit ~ 64bit 이상부터는 성능 향상이 둔화
- 일정 수준 이상에서는 정확도 증가가 미미함

즉, 성능 향상은 있으나 한계가 존재함

IVF, Inverted File Index

구분	내용
구조	데이터 클러스터링 기반 (예: K-means)
사용 예시	영상 검색, 문서 검색, 이미지 인식
원리	- 전체 벡터 데이터를 여러 개 클러스터로 나눔 - 쿼리 벡터가 속할 가능성이 높은 몇 개의 클러스터만 탐색 - 각 클러스터는 중심점(centroid)을 대표 벡터로 사용 - 쿼리 벡터와 중심점 간 거리 비교 후 유사한 클러스터 선택 - 선택된 클러스터 내부에서만 KNN 검색 수행
장점	- 빠른 검색 속도 (탐색 범위 축소) - 효율적인 메모리 관리 (인덱스 구축 시간 및 메모리 사용량 증가 가능성 있음)
단점	- 정확도는 클러스터 품질에 의존 - 탐색할 클러스터 수(nprobe)가 많을수록 정확도는 향상되나 검색 속도는 저하됨

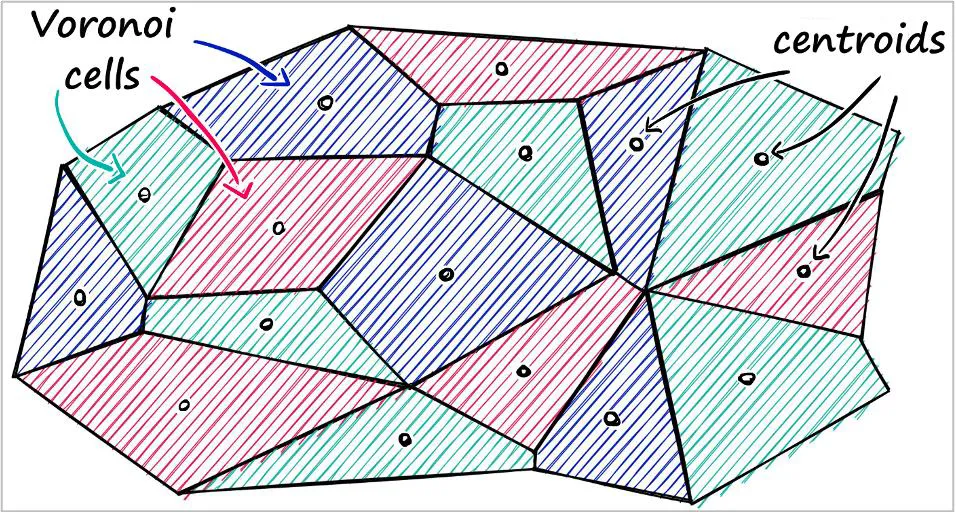
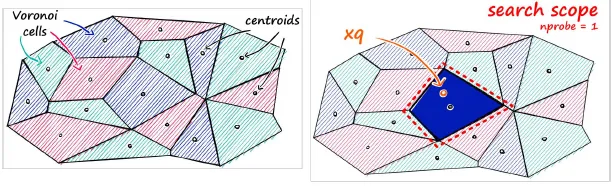
Voronoi Cell 기반 분할 (IVF 구조)

항목	설명
기본 원리	전체 벡터 공간을 K-means 알고리즘으로 분할하여 Voronoi Cell(보로노이 셀) 생성
구조	각 셀은 centroid(중심점)를 기준으로 가장 가까운 벡터들이 모여 있음
탐색 방식	검색 시, 먼저 쿼리 벡터와 가장 가까운 centroid를 찾고 → 해당 셀 내부에서만 탐색 수행

IVF의 핵심은 검색 범위를 셀 단위로 줄여 속도를 향상시키는 것이며, 클러스터링 기반의 효율적인 인덱싱 구조

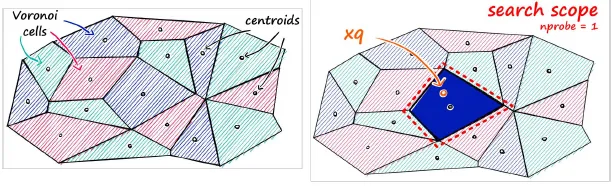
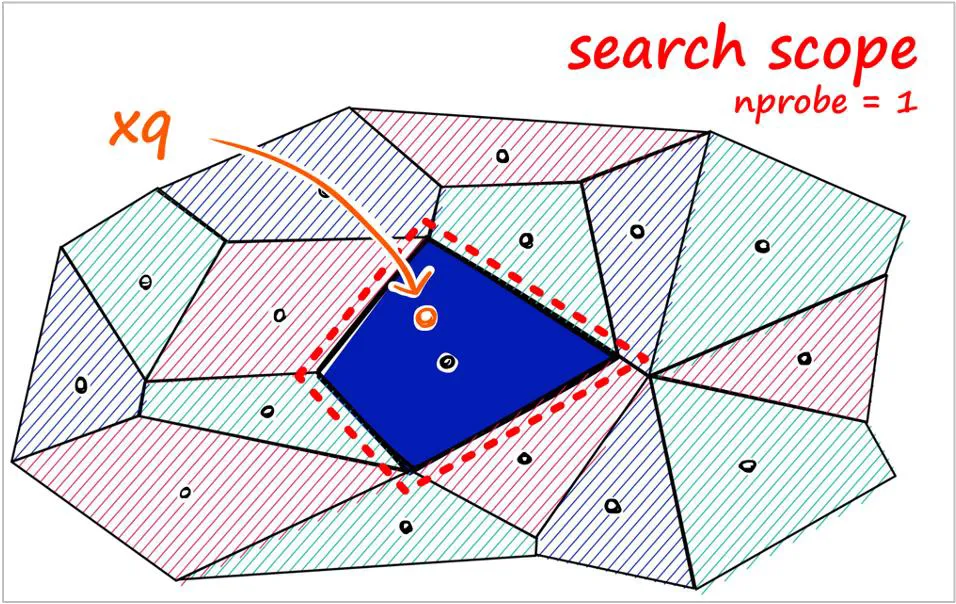
nprobe = 1일 때 (IVF 탐색 설정)

항목	설명
탐색 범위	쿼리 벡터 `xq`는 가장 가까운 하나의 셀만 탐색 (예: 파란 셀 영역)
장점	탐색 속도가 매우 빠름
단점	- 정확도가 낮아질 수 있음
- 근처에 유사한 벡터가 있어도 다른 셀에 있다면 탐색되지 않을 수 있음

nprobe=1은 속도 우선 전략이며, 정확도는 희생될 수 있음

nprobe = 8일 때 (IVF 탐색 설정)

항목	설명
탐색 범위	쿼리 벡터 `xq` 주변의 8개 셀을 함께 탐색
정확도	Recall(정확도) 향상됨 → 유사 벡터를 찾을 확률 증가
속도	연산량이 많아져 속도는 느려짐
추가 특징	`nprobe` 값이 클수록 더 넓은 영역을 커버함

nprobe=8은 정확도 우선 전략으로, 속도를 일부 희생하더라도 유사 벡터를 더 놓치지 않고 찾기 위함

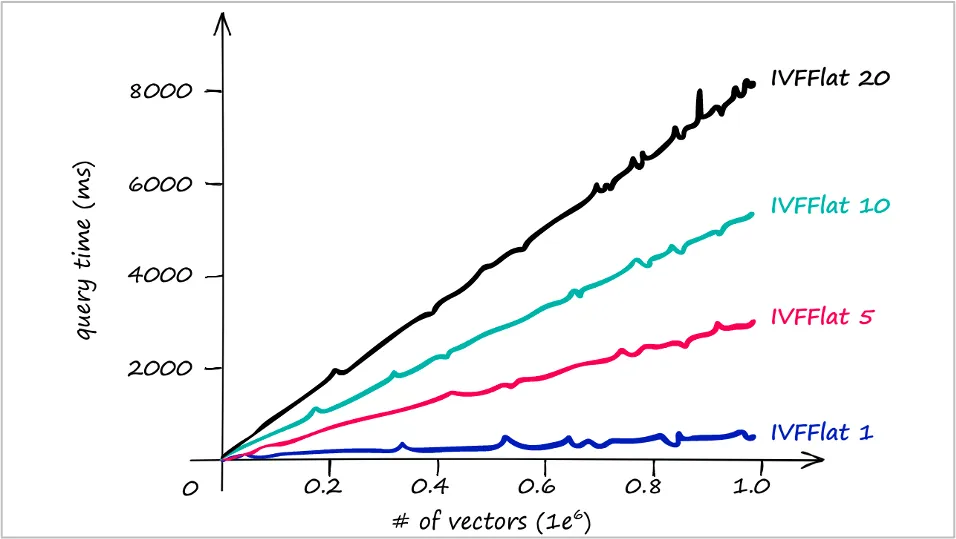
IVF 성능 그래프 해석

항목	설명
x축	벡터 수 (단위: 1e6 = 백만 개)
y축	쿼리 소요 시간 (단위: ms)
탐색 셀 수 변화	탐색하는 셀 수에 따라 성능이 달라짐

IVFflat 1: 빠르지만 정확도 낮음
IVFflat 20: 느리지만 정확도 높음

속도 vs 정확도 트레이드오프 존재

IVF 관련 주요 용어 정리

용어	설명
IVF (Inverted File Index)	- 벡터를 K개의 클러스터로 나눈 뒤, 일부 클러스터만 검색 - 검색 시 탐색할 클러스터 수 지정
nprobe	- 탐색할 클러스터 수- `nprobe = 1`: 빠르지만 정확도 낮음 - `nprobe ↑`: 느려지지만 정확도 상승 - 적절한 `nprobe` 선택은 속도/정확도 균형 조절의 핵심
centroid	각 클러스터의 중심점
Voronoi cell	중심점 기준으로 벡터가 소속되는 영역
IVFflat	IVF 구조에서 각 클러스터 내부를 Flat(정확히) 방식으로 검색

PQ

구분	내용
구조	압축 기반 인코딩
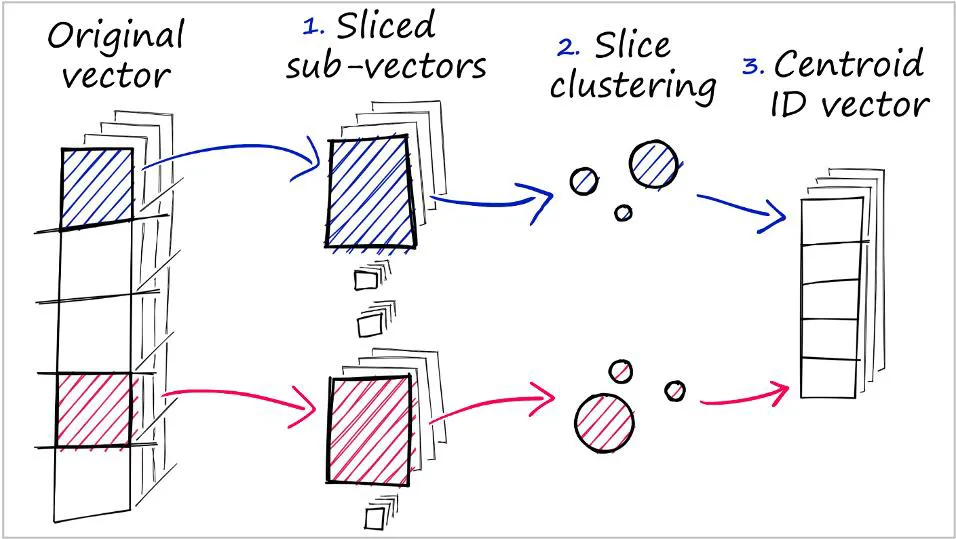
원리	- 벡터를 여러 블록으로 나누고, 각 블록을 압축 코드북(codebook)으로 표현 - 예: 128차원 벡터 → 8개 블록 → 각 블록을 코드북에서 대표값으로 대체 - 보통 K-means를 활용해 각 블록별 코드북 생성- 고차원 벡터 → 저차원 서브벡터로 분할 → 각 서브벡터를 양자화하여 저장
장점	- 대용량 벡터 처리에 적합- 메모리 절약 + 거리 계산 속도 향상
단점	- 약간의 정확도 손실 발생 가능 - 설정 및 튜닝 필요 (코드북 수, 블록 수 등)
활용	각 서브벡터는 코드북 인덱스로 표현되며, IVF와 함께 사용 가능 (IVFPQ 등)

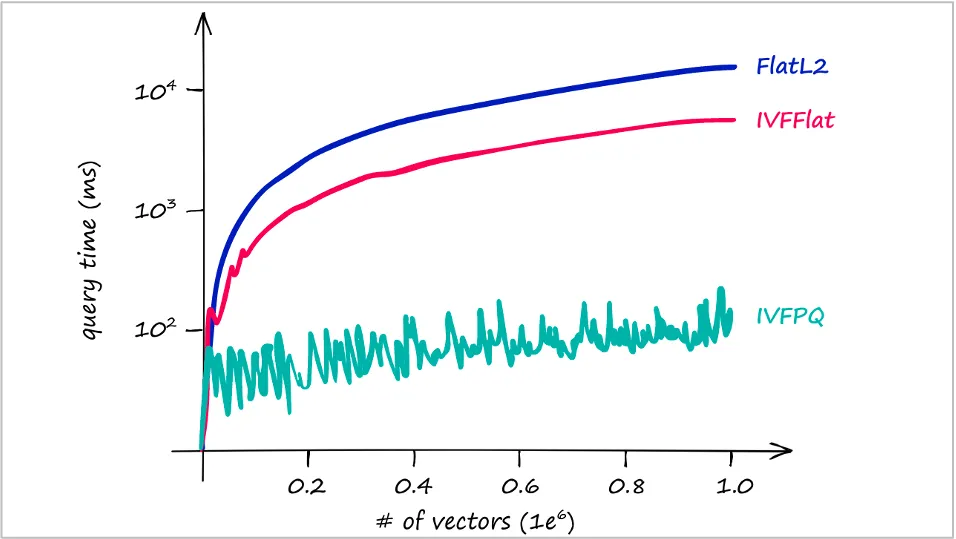
인덱스 방식별 비교

인덱스 방식	설명	특징
FlatL2	모든 벡터를 정확히 비교	느리지만 정확도 높음
IVFFlat	IVF 구조 기반, 선택된 셀만 정밀 비교	빠르고, 정확도는 중간 수준
IVFPQ	IVF + PQ 압축 구조	가장 빠름, 정확도는 약간 손실 가능

요약 포인트

IVFPQ: 벡터 수가 많아져도 시간 증가 거의 없음 → 대규모 데이터에 적합
FlatL2: 가장 정확하지만, 데이터 많을수록 기하급수적으로 느려짐
IVFFlat: 속도·정확도 균형 잡힌 선택지

HNSW

HNSW 정리

항목	설명
구조	계층적 그래프 기반
사용 예시	벡터 검색, 추천 시스템, 문서 검색 등

<원리>

데이터 포인트를 노드로 간주, 이들 간 근접성 기반 그래프 구성
계층 구조로 구성되며, 상위 레벨일수록 노드 수는 적고 연결은 추상적
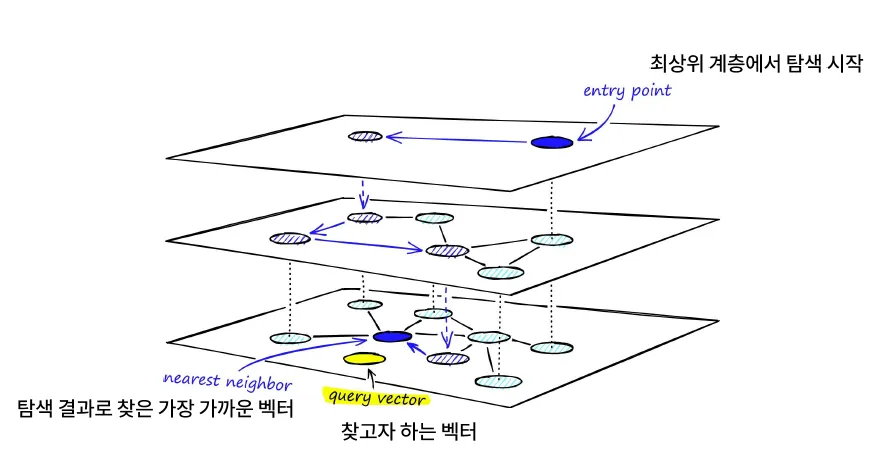
검색은 최상위 레벨부터 시작, 점점 하위 레벨로 내려가며 이웃 노드를 탐색
각 단계에서 가장 가까운 노드로 이동하면서 목표 벡터에 점차적으로 접근

<장점>

정확도 매우 높음 (95~99%)
속도도 빠름

<단점>

메모리 사용량 큼
구조 구축 시간 오래 걸리고 구현 복잡도 높음

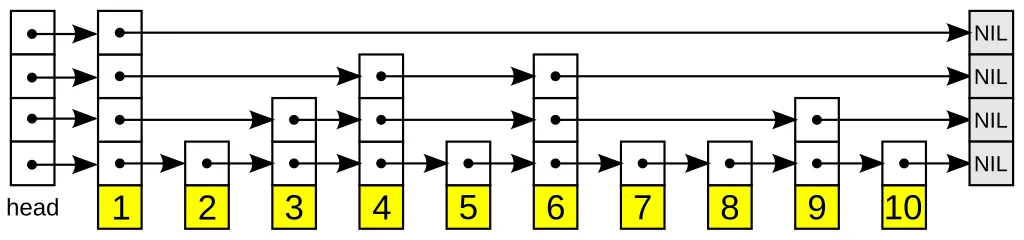
Skip List: 일종의 계층형 연결 리스트

개념

기본 연결 리스트는 노드를 순서대로 연결
Skip List는 "건너뛸 수 있는 고속도로" 개념

→ 상위 레벨 링크를 추가하여 일부 노드를 건너뛰며 탐색 속도 향상

구조

Balanced Tree와 Linked List의 장점을 결합한 자료 구조

탐색 흐름

최상위 레벨에서 시작
다음 노드의 키와 검색하려는 값 비교
- 다음 키가 작으면 오른쪽으로 이동
- 다음 키가 크면 하위 레벨로 이동
가장 하위 레벨에 도달할 때까지 반복

Navigable Small World (NSW)

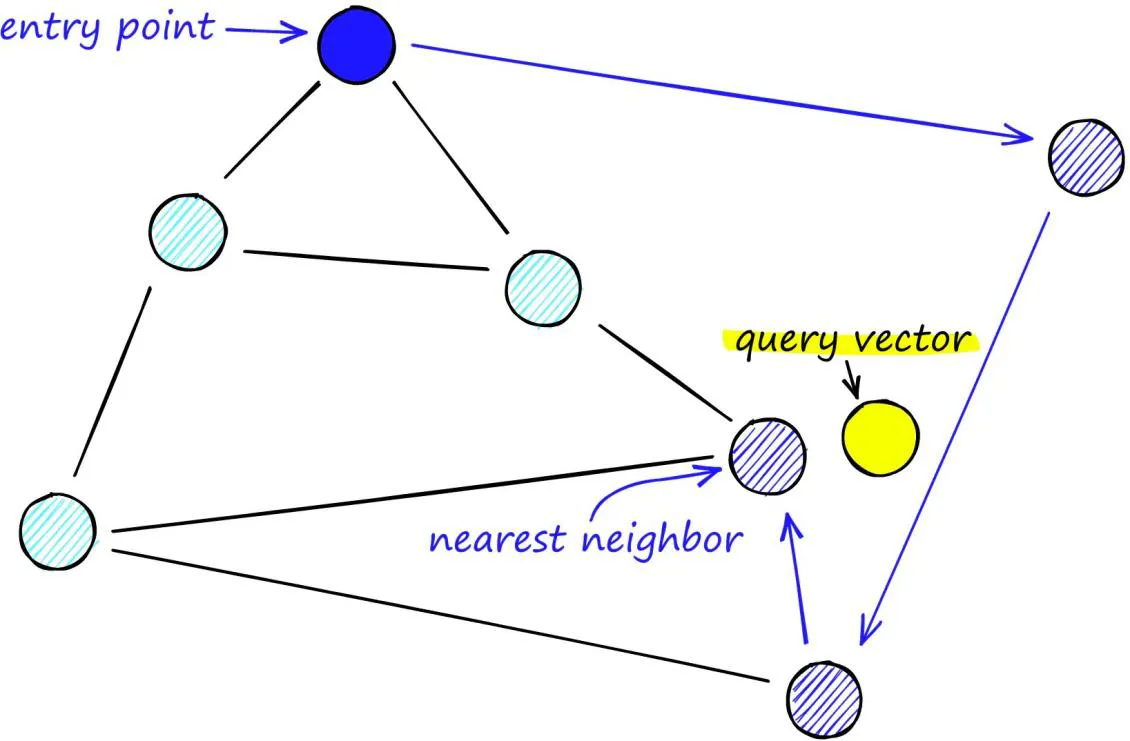
개념

네트워크 구조에서 효율적인 검색과 탐색을 가능하게 하는 데이터 구조 및 알고리즘 개념
전체 노드가 넓게 퍼져 있어도, 몇 번의 연결만으로 거의 모든 노드에 도달할 수 있음
각 노드는 k개의 이웃 노드와 연결되어 있으며,
- long-range 연결과 short-range 연결을 조합하여 구성됨
가까운 노드만 따라가도 목표 노드에 도달 가능

예시

SNS(소셜 네트워크)
- “세상은 좁다”는 말처럼 대부분의 사람은 6단계 이내로 연결됨 ("6 degrees of separation")

탐색 흐름

쿼리 벡터가 입력되면
상위 레벨에서 출발 (멀리 있는 친구들부터 시작)
가까운 노드를 따라 이동
- 점점 정확히 위치를 좁혀가며
- 최종적으로 목표에 가까운 노드에 도달
- 위 과정을 목표 도달 시까지 반복

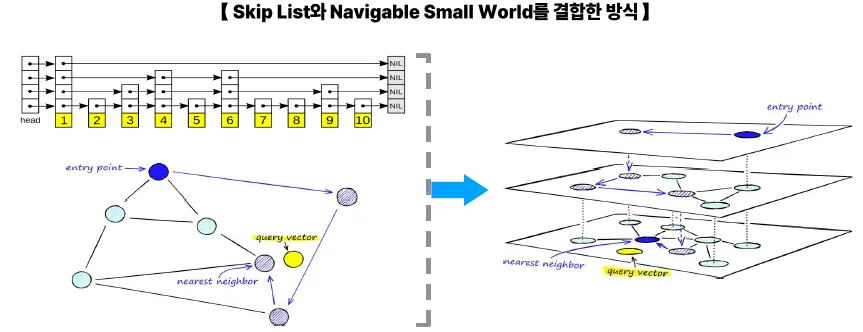
NHSW는 Skip List에서 아이디어를 얻었지만, 훨씬 더 강력한 그래프 탐색 구조로 발전했다.

업로드중..

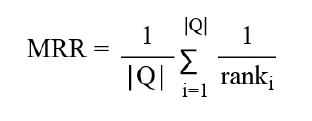
import nmslib

index = nmslib.init(method='hnsw', space='cosinesimil')

# 데이터 추가
index.addDataPointBatch(data)

# HNSW 파라미터 설정
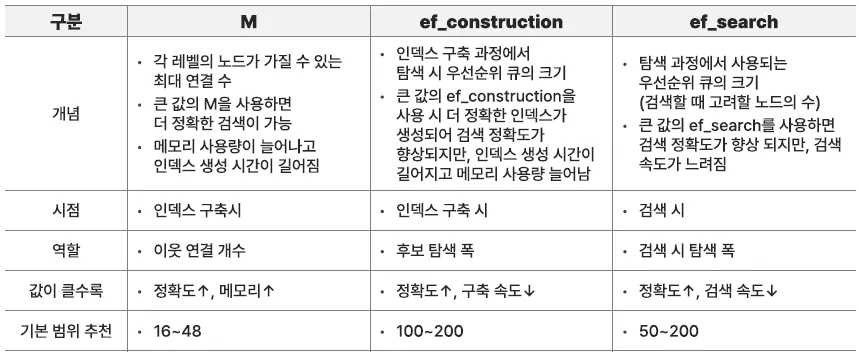
index.createIndex({
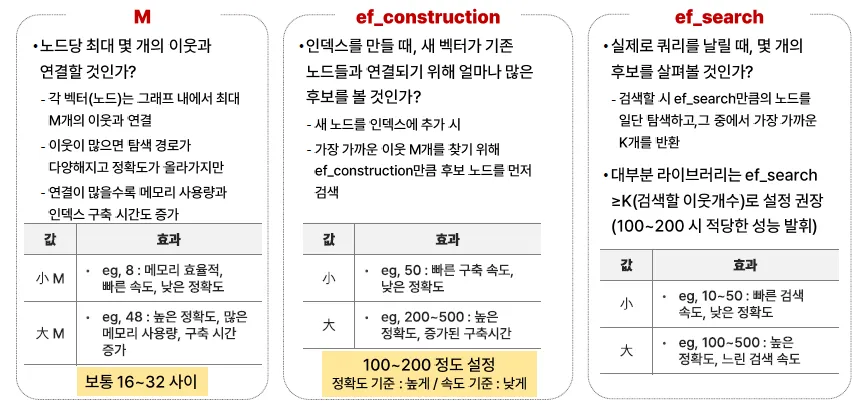
    'M': 32,
    'efConstruction': 200
}, print_progress=True)

# ef_search 설정
index.setQueryTimeParams({
    'efSearch': 100
})

상황	추천 설정
정확도 중요 시	- `M = 48` - `ef_construction = 300` - `ef_search = 200 ~ 500`
속도 중요 시 (실시간)	- `M = 16` - `ef_construction = 100` - `ef_search = 50 ~ 100`
중간 수준	- `M = 32` - `ef_construction = 200` - `ef_search = 100 ~ 150`

ANN 알고리즘 평가지표

MRR, Mean Reciprocal Rank

정답(정답 벡터, relevant item)이 검색 결과 중 몇 번째에 나오는지를 평가하는 지표**