머신러닝 독학하기 - 선형 회귀와 경사 하강법

시작에 앞서...

딥러닝은 기계학습의 한 종류로 인공신경망을 여럿 쌓는 것입니다. 인공신경망은 어떤 입력을 받아 특정 출력을 뱉는 일종의 함수로 기능합니다. 그리고 이 층층이 쌓인 인공신경망은 데이터를 받아 스스로 학습하면서 성능이 개선됩니다. 선형 회귀는 딥러닝 알고리즘의 가장 기초적인 알고리즘 중 하나입니다. 여기서는 정직하게 코딩하며 배우는 딥러닝 입문을 참고했습니다.

선형 회귀

선형 회귀는 아주 간단한 1차 함수로 표현할 수 있습니다.

$y = ax + b$

선형 회귀는 이 1차함수를 이용합니다. 입력 x와 출력 y 여럿이 있는 데이터셋이 있을 때 이 데이터로 가장 정답에 가까운 기울기 a와 절편 b를 찾는 것이 선형 회귀의 목표입니다.

경사 하강법

경사 하강법은 어떤 손실 함수가 정의되었을 때 손실함수의 값이 최소가 되는 지점을 찾아가는 방법입니다.

선형 회귀의 목표를 다시 생각해보겠습니다. 우리의 목적은 정답에 가까운 기울기와 절편을 찾는 것입니다. 즉, 다른 말로 표현하면 오차가 가장 적은 기울기와 절편을 찾는 것이고 손실함수는 이 오차가 됩니다. 대부분의 경우 아주아주 높은 확률로 임의의 기울기와 절편으로 만든 식에 실제 데이터 $x_1$, $y_1$은 맞아 들어가지 않습니다. 실제 데이터와 다르게 식이 예측하는 결과를 $\breve{y}$이라고 정하겠습니다. 그렇다면 식과 오차는 다음과 같습니다.

$\breve{y} = ax + b$
$\breve{y} - y_1$

우리는 오차의 절댓값이 가장 적은 것이 목표이므로 위 오차에 제곱을 취해주겠습니다. 그렇다면 손실함수는 다음과 같습니다.

$(\breve{y} - y_1)^2$
$(ax_1 + b - y_1)^2$

이 함수의 최솟값을 알아내기 위해서는 기울기에 따라 함수의 값이 낮은 쪽으로 이동해야 합니다. 기울기는 미분을 통해 구할 수 있습니다. 먼저 $a$에 대해 기울기를 구해봅시다.

$\frac{\mathrm{d}(\breve{y} - y)^2}{\mathrm{d}a}$ = $2(\breve{y} - y)(\frac{\mathrm{d}\breve{y}}{\mathrm{d}a})$ = $2(\breve{y} - y)x$

이 값이 $a$가 1 증가할 때마다 손실 함수가 증가하는 정도 즉 변화율입니다. 우리는 손실함수의 최소로 이동하고 싶기 때문에 이 값을 뺍니다. 상수를 손실함수에 곱하거나 나누어도 최종 모델에 영향을 미치지 않기 때문에 변화율을 2로 나누어서 사용하겠습니다. 이 값으로 변화율을 업데이트 하겠습니다.

$a = a + (y - \breve{y})x$

다음으로 $b$에 대해 기울기를 구해봅시다

$\frac{\mathrm{d}(\breve{y} - y)^2}{\mathrm{d}b}$ = $\frac{1}{2}(\breve{y} - y)(\frac{\mathrm{d}\breve{y}}{\mathrm{d}b})$ = $(\breve{y} - y)$

b를 업데이트 합시다.

$b = b + (y - \breve{y})$

코드로 적용하기

사이킷런의 당뇨병 데이터와 maplotlib를 사용하겠습니다.

# 데이터, 모듈 불러오기
from sklearn.datasets import load_diabetes
import matplotlib.pyplot as plt
diabetes = load_diabetes()

# 초기화
a , b = 1, 1

# 업데이트 반복
for x in range(100):
	for x_i, y_i in zip(diabetes.data[:, 2], diabetes.target):
    		y_hat = x_i * a + b
          	err = y_i - y_hat
          	a = a + x_i * err
          	b = b + err
 
# 결과 확인
# 산점도 그래프
plt.scatter(x, y)

# x 값을 아무거나 집어넣고 직선 위 두 점을 구함
pt1 = (-0.1, -0.1 * w + b)
pt2 = (0.15, 0.15 * w + b)

# 직선 위 두 점으로 직선을 그림
plt.plot([pt1[0], pt2[0]], [pt1[1], pt2[1]])
plt.xlabel('x')
plt.ylabel('y')
plt.show()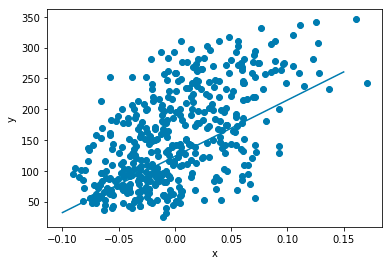

여기서 코드 상에서 for문 1회로 일어나는 변화 전파 한 단위를 에포크(epoch)라고 합니다. 또한 변화율은 인공지능 분야에서는 그래디언트(gradient)라고도 부릅니다. 그리고 업데이트에 오차(여기서는 $y - \breve{y}$, y_i - y_hat)이 반영되는 것을 오차역전파(backpropagation)라고 부릅니다.

개인적으로 남은 의문점

1. 다른 값으로도 경사 하강이 가능한데 하필 변화율을 사용하는 이유

이 글은 개인 공부 목적으로 작성하였습니다. 오류가 있을 수도 있으니 있다면 댓글로 남겨주시면 감사하겠습니다.