🎲[AI] Gradient 기반 Optimizer 정리 (feat. 모르겠으면 Adam 써라!)

해당 글은 FastCampus - '[skill-up] 처음부터 시작하는 딥러닝 유치원 강의를 듣고,
추가 학습한 내용을 덧붙여 작성하였습니다.

---

1. Learning Rate

1.1 Learning Rate의 특성

Gradient descent 수식

$\theta ← \theta - \eta \nabla _ \theta L(\theta)$
$\eta$: Learning rate

• 큰 LR: 발산 위험
• 작은 LR: 수렴 속도 느림, local minima에 갇힘 가능성(파라미터 수가 많지 않을 경우)
• 궁극적으로 Loss surface의 형태를 알 수 없기 때문에 최적의 learning rate를 알기 어려움

1.2 Learning Rate Scheduling

• 학습 초반에는 큰 LR, 후반에는 작은 LR으로 최적화하는 방법
• 하지만, 큰 LR의 기준은? 초반/후반을 나누는 기준은?
  → 오히려 Hyper parameter가 더 많아질 수 있음

---

2. Optimizer 알고리즘들

2.1 알고리즘 계략도

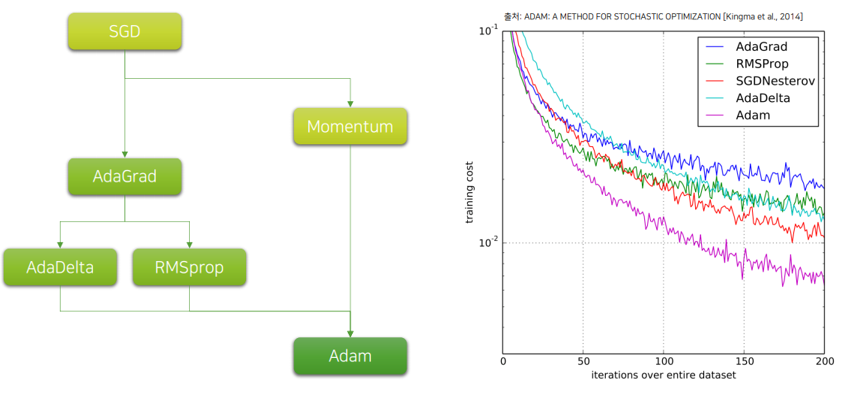
Optimizer	특징
SGD	기본적이며 안정적이지만 튜닝 필요
Momentum	관성 적용, 수렴 가속
AdaGrad	파라미터별 학습률 자동 조절
RMSProp	최근 gradient 기반 학습률 조절
Adam	Momentum + AdaGrad, 높은 성능

2.2 SGD with Momentum

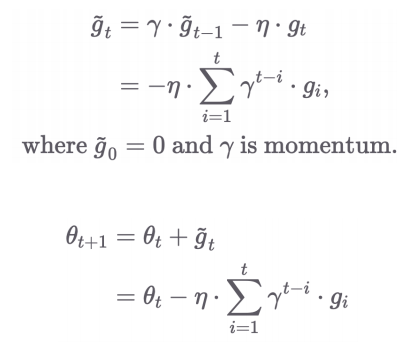
• 이전 gradient를 일정 비율($\gamma$) 반영하여 더 빠른 수렴 유도
• 관성을 이용해 local minima 탈출 가능
  

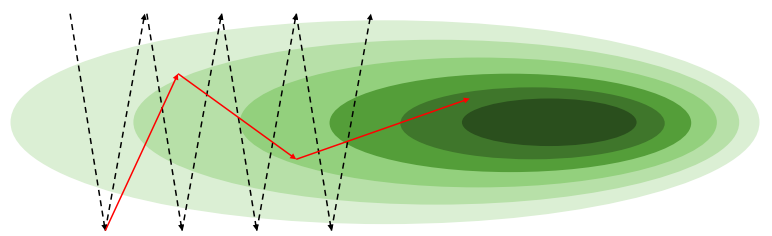
2.3 AdaGrad

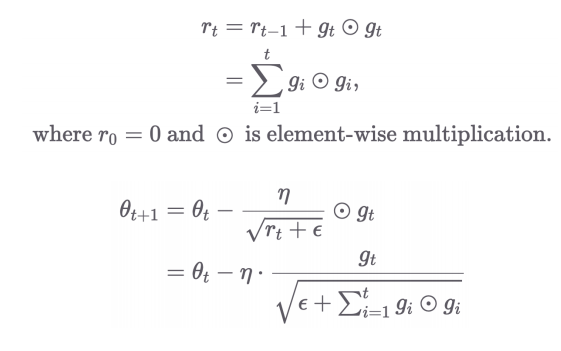
• 파라미터별로 각각의 Learning rate를 가짐
• $g_t \circ g_t$는 그냥 $g_t^2$ 생각하면 됨
• $\epsilon$은 0 방지하기 위한 숫자
• $g_1$ ~ $g_t$까지의 L2 Norm을 통해 현재 $g_t$의 학습률 조정
• 지금까지의 gradient가 컸으면 현재 gradient는 작게 조정됨
• 즉, 파라미터별 누적 gradient의 제곱합으로 학습률 조정
  → 학습이 진행될수록 LR이 작아짐

2.4 RMSProp / AdaDelta

• AdaGrad의 단점(학습률이 너무 빨리 작아지는 문제)을 보완
• 이전 gradient 전체의 누적합 대신, 최근 gradient 제곱의 지수이동평균을 사용
  → 학습률이 너무 빨리 줄어드는 현상 방지
• 이로 인해 안정적이고 빠른 수렴 가능

• RMSProp은 고정된 learning rate 사용,
• AdaDelta는 RMSProp 기반, learning rate 없이 스스로 업데이트 크기 조절

2.5 Adam (Adaptive Moment Estimation)

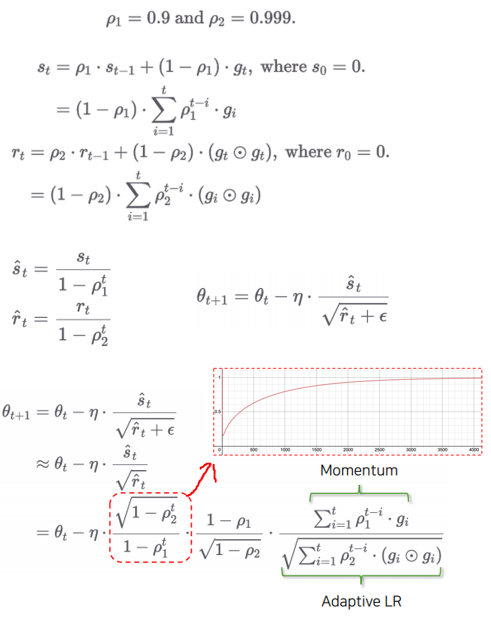
• Momentum + AdaGrad 결합
• $\rho_1$, $\rho_2$, $\eta$의 hyper parameter들을 가짐
  → Default 값을 써도 무방하지만, 매~~~우 정교한 모델에서는 역시 튜닝이 필요함
• $s_t$: Momentum, $r_t$: LR
• 빠른 수렴과 안정성 제공
• 현재 가장 널리 사용됨

---

3. Pytorch 소스 코드

import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
from sklearn.preprocessing import StandardScaler
import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
from sklearn.datasets import fetch_california_housing

california = fetch_california_housing()

df = pd.DataFrame(california.data, columns=california.feature_names)
df["Target"] = california.target
# df.tail()

# sns.pairplot(df.sample(1000))
# plt.show()

scaler = StandardScaler()
scaler.fit(df.values[:, :-1])
df.values[:, :-1] = scaler.transform(df.values[:, :-1])

# sns.pairplot(df.sample(1000))
# plt.show()

data = torch.from_numpy(df.values).float()

print(data.shape)

x = data[:, :-1]
y = data[:, -1:]

print(x.shape, y.shape)

n_epochs = 4000
batch_size = 128
print_interval = 200
# learning_rate = 1e-5 필요 X

model = nn.Sequential(
    nn.Linear(x.size(-1), 10),
    nn.LeakyReLU(),
    nn.Linear(10, 9),
    nn.LeakyReLU(),
    nn.Linear(9, 8),
    nn.LeakyReLU(),
    nn.Linear(8, 7),
    nn.LeakyReLU(),
    nn.Linear(7, 6),
    nn.LeakyReLU(),
    nn.Linear(6, 5),
    nn.LeakyReLU(),    
    nn.Linear(5, 4),
    nn.LeakyReLU(),
    nn.Linear(4, 3),
    nn.LeakyReLU(),
    nn.Linear(3, y.size(-1)),
)

print(model)

optimizer = optim.Adam(model.parameters(),)

# |x| = (total_size, input_dim)
# |y| = (total_size, output_dim)

for i in range(n_epochs):
    #  the index to feed-forward.
    indices = torch.randperm(x.size(0)) # Shuffle
    x_ = torch.index_select(x, dim=0, index=indices) # x와 y indices 동일하게 써야 함
    y_ = torch.index_select(y, dim=0, index=indices)
    
    x_ = x_.split(batch_size, dim=0)
    y_ = y_.split(batch_size, dim=0)
    # |x_[i]| = (batch_size, input_dim)
    # |y_[i]| = (batch_size, output_dim)
    
    y_hat = []
    total_loss = 0
    
    for x_i, y_i in zip(x_, y_):
        # |x_i| = |x_[i]|
        # |y_i| = |y_[i]|
        y_hat_i = model(x_i)
        loss = F.mse_loss(y_hat_i, y_i)

        optimizer.zero_grad()
        loss.backward()

        optimizer.step()
        
        total_loss += float(loss) # Gradient graph 끊어짐 → float로 변환해서 memory leak 방지
        y_hat += [y_hat_i]

    total_loss = total_loss / len(x_)
    if (i + 1) % print_interval == 0:
        print('Epoch %d: loss=%.4e' % (i + 1, total_loss))
    
y_hat = torch.cat(y_hat, dim=0)
y = torch.cat(y_, dim=0)
# |y_hat| = (total_size, output_dim)
# |y| = (total_size, output_dim)

df = pd.DataFrame(torch.cat([y, y_hat], dim=1).detach().numpy(),
                  columns=["y", "y_hat"])

sns.pairplot(df, height=5)
plt.show()