딥러닝 (3)

Chapter 3 인공신경망

인공신경망 (Artificial Neural Network) 소개

• 인간 두뇌의 신경망 구조를 모방하여 구현한 머신 러닝 모델
  -> 신경이 서로 연결된 강도(시냅스 연결 강도시냅스 연결 강도)에 따라 논리적인 동작이 달라지는 것을 모방
  -> 은닉 계층(hidden layer)으로 인해 선형적으로 구분되지 않는 학습 샘플을 분류할 수 있음

• 인공신경망은 신경(neuron)끼리 서로 연결된 강도인 가중치(weight)를 학습하여 논리적을 판단을 하거나 회귀 등의 동작을 구현
  

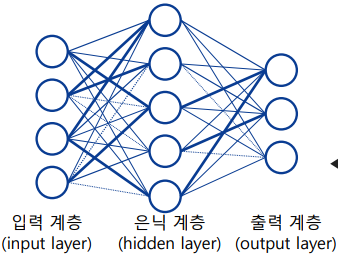
인공신경망의 애플리케이션

• 학습 데이터의 구성에 따라 다양한 모델을 학습할 수 있음
  -> 출력을 0 또는 1로 하여 이진 분류 모델 학습
  -> 출력을 실수 값으로 하여 회귀 모델 학습
  -> 출력을 원핫벡터(one-hot vector)로 구성하여 다중 분류 모델 학습
  

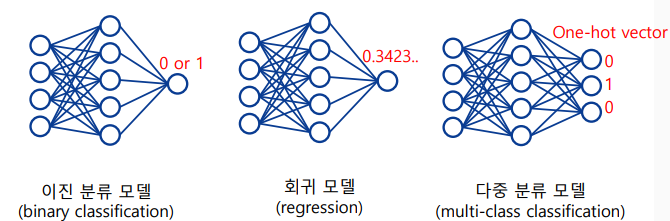
-> 이진 분류 모델은 logstic regression과 유사

퍼셉트론

• 신경 세포와 퍼셉트론

• 퍼셉트론 (Perceptron)은 신경 세포(neuron)를 이진 출력의 단순한 논리 게이트로 해석하여 고안한 알고리즘
  

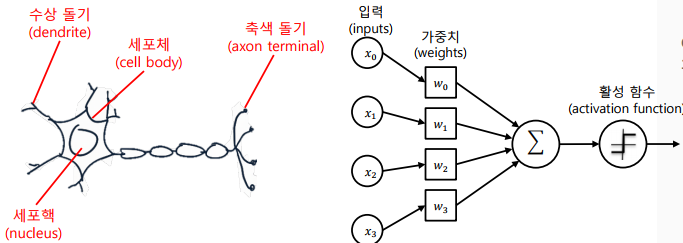
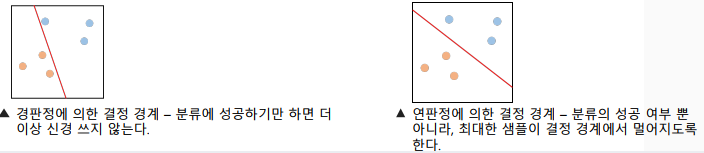
• 퍼셉트론은 결정 경계(decision boundary)를 표현할 수 있음
  -> 로지스틱 회귀와 달리 경판정 방식을 사용
  -> 경판정(hard decision): 중간 값 없이 단일 기준으로 딱 잘라 나누는 방식
  

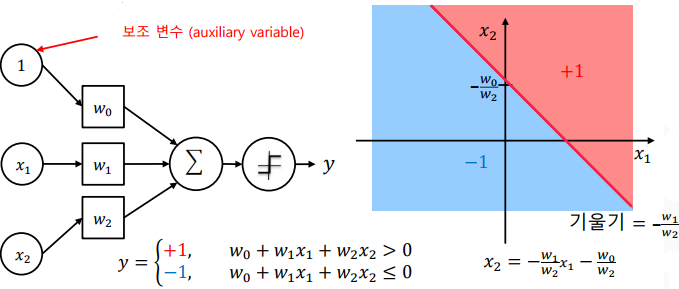
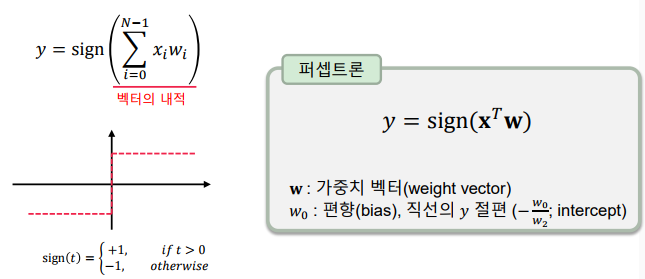
• 퍼셉트론은 벡터 내적과 부호 함수(sign function)으로 표현
  -> 머신 러닝에서 배운 로지스틱 회귀와 유사하나, 출력 값이 -1 또는 +1로 정해진다는 점이 다름
  

• 퍼셉트론의 손실 함수 (loss function)
  -> 학습을 할 때 더 작아지게 하고자 하는 목표 함수
  -> 정답과 활성 이전의 값 곱의 총합의 부호 반전을 손실 함수로 사용
  -> 정답을 맞추지 못한 경우에만 손실 함수에 포함
  

퍼셉트론의 학습

• 손실 함수를 𝐰(가중치)로 미분하여 경사하강법(gradient descent) 수행
  -> 각 샘플을 평가할 때 마다 경사하강법을 1-step씩 수행
  

퍼셉트론의 구현

import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_classification

X, y = make_classification(n_samples=100,           # number of samples
                           n_features=2,            # feature dimension
                           n_informative=2,         # informative dimensions
                           n_redundant=0,           # redundant dimensions
                           n_classes=2,             # number of classes
                           n_clusters_per_class=1,  # cluster per class
                           class_sep=2.0,           # class separability
                           random_state=20)
                           
y = 2 * y - 1  # convert labels from {0, 1} to {-1, 1}                     X.shape    

(100, 2)

plt.scatter(X[:,0], X[:,1], c=y)
plt.title('Groundtruth')
plt.show()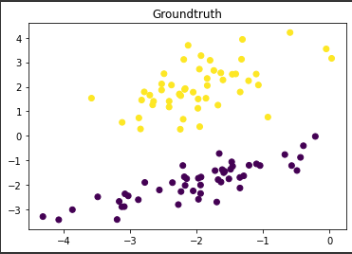

class Perceptron(tf.Module):
    def __init__(self, **kwargs):  # defines variables and layers
        super().__init__(**kwargs)  # call constructor of tf.Module
        self.w = tf.Variable(tf.random.normal([2,1], dtype=tf.float32))  # weight variable
        self.b = tf.Variable(0.0, dtype=tf.float32)                      # bias variable

    def __call__(self, x):  # defines feed-forward operation
        return tf.reduce_sum(tf.transpose(self.w)*x, axis=1) + self.b

model = Perceptron()

model.w

<tf.Variable 'Variable:0' shape=(2, 1) dtype=float32, numpy=
array([[0.1900148 ],
[0.79189396]], dtype=float32)>

model.b

<tf.Variable 'Variable:0' shape=() dtype=float32, numpy=0.0>

z = model(X)
tf.sign(z)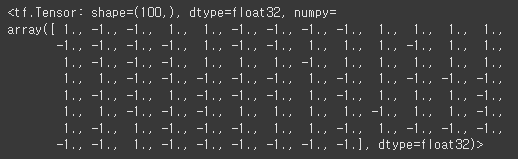

def loss_func(y_true, y_pred, z):
    return -(y_true - y_pred) * z  # loss function of perceptron
    
def train_step(model, X, y, eta):
    for x, y_true in zip(X, y):
        with tf.GradientTape() as t:  # calculate gradients in this context
            z = model(x)                         # feed-forward operation
            y_pred = tf.sign(z)                  # applying activation function
            loss = loss_func(y_true, y_pred, z)  # calculating loss function
        
        dw, db = t.gradient(loss, [model.w, model.b])  # get gradient of weight and bias

        model.w.assign_sub(eta*dw)  # apply gradient descent on weight (w = w - eta*dw)
        model.b.assign_sub(eta*db)  # apply gradient descent on bias   (b = b - eta*db)
        
train_step(model, X, y, eta=0.1)  # train using all samples

plt.scatter(X[:,0], X[:,1], c=tf.sign(model(X)))
plt.title('Classification by Perceptron')
plt.show()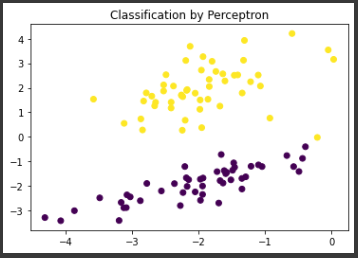

활성함수 (Activation functions)

• 이전 함수의 출력에 의미를 부여하는 역할을 하는 함수

• 다양한 목적의 활성 함수
  -> 회귀를 위한 활성 함수 (linear activation = identity function)
  -> 경판정 이진 분류를 위한 활성 함수 (sign function)
  -> 연판정 이진 분류를 위한 활성 함수 (tanh, sigmoid)
  -> 다중 분류를 위한 활성 함수 (softmax)
  -> 중간 출력에 비선형 매핑을 위한 활성 함수 (ReLU: Rectified Linear Unit)
  

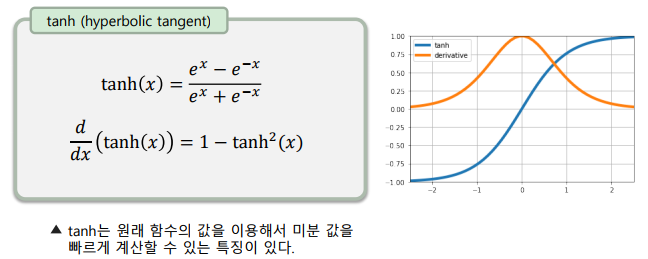
• Hyperbolic Tangent(tanh)
  -> 연판정(soft decision) 활성 함수로, 판정이 잘 되는 ‘정도’를 표현
  -> 값이 작아질 수록 -1, 커질 수록 1에 수렴
  -> 입력 값이 0에 가까운 지점에서 출력이 빠르게 변함
  

• Sigmoid
  -> 연판정(soft decision) 활성 함수로, 판정이 잘 되는 ‘정도’를 표현
  -> 출력이 0.0 ~ 1.0 사이로, ‘확률’을 표현할 수 있음
  -> 입력 값이 0에 가까운 지점에서 출력이 빠르게 변함
  

• Softmax
  -> 다중 클래스 분류를 위한 활성 함수로, 입력과 출력의 개수가 같음
  -> 각 출력은 0.0 ~ 1.0 사이의 값을 가지며, 모든 값의 합은 반드시 1
  -> 여러 클래스 중 한가지에 속할 확률을 표현
  -> 머신 러닝에서는 잘 쓰이지 않았지만, 딥러닝에서는 빈번히 사용됨
  

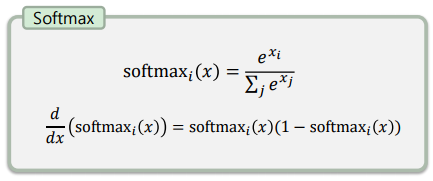
• ReLU
  -> 0보다 작은 값을 0으로 대체하는 매우 간단한 활성 함수
  -> 딥러닝에서 가장 많이 사용되는 활성 함수로, 비선형 특성을 부여
  -> 미분값이 일정(0 또는 1)하기 때문에 학습이 잘 되는 특성이 있음
  -> 구현이 단순하여 매우 빠른 연산이 가능
  

손실함수(Loss Function)

• cost function, objective function, energy function

• 최적화(최소화)의 대상이 되는 함수로, 인공신경망 학습을 위해 반드시 정의되어야 함

• 해결하고자 하는 문제에 맞는 적절한 손실 함수를 선택해야 함
  

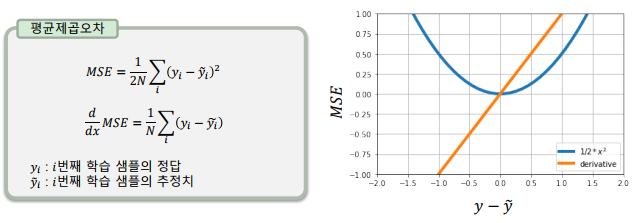
• 평균 제곱 오차(MSE: Mean Squared Error)
  -> 가장 기본적인 손실 함수로, 미분이 쉬움
  -> 오차가 커질수록 손실함수가 빠르게 증가
  -> 회귀(regression) 알고리즘의 학습에 많이 사용됨
  

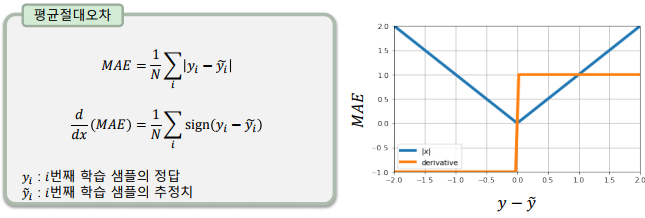
• 평균 절대 오차(MAE: Mean Absoulte Error)
  -> 오차가 커져도 손실 값이 일정하게 증가
  -> 이상치(outlier)에 강건한(robust) 특징이 있음
  -> 회귀(regression) 알고리즘의 학습에 많이 사용
  

• 교차 엔트로피 오차(CEE: Cross Entropy Error)
  -> 소프트맥스 활성 함수 출력을 평가하기 위해 사용
  -> 정답은 원핫 인코딩(one-hot encoding)을 사용
  -> 원핫 인코딩에 의해 정답인 클래스에서만 손실 함수 값이 발생
  

전결 합계층

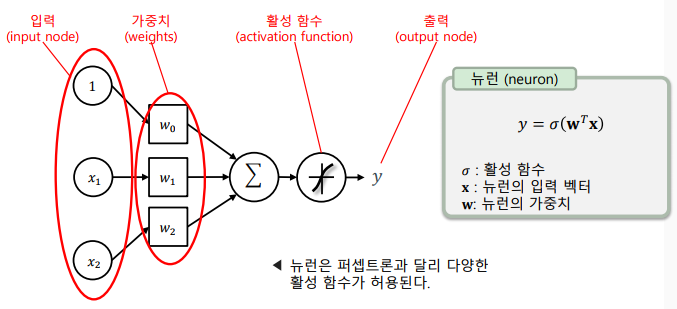
• 뉴런: 인공신경망의 기본이 되는 단위로 입력의 개수는 제한이 없으며 출력은 하나만을 가짐
  

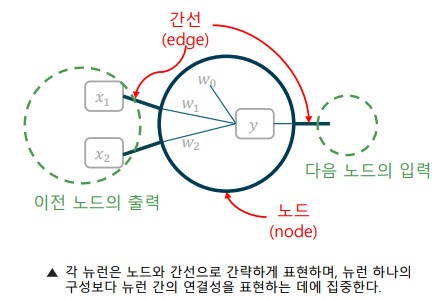
• 뉴런의 그래프 표현(자료 구조)
  -> 뉴런을 그래프의 노드(node)와 간선(edge)로 표현
  -> 노드는 뉴런의 연산을, 간선은 뉴런간의 연결을 표현
  

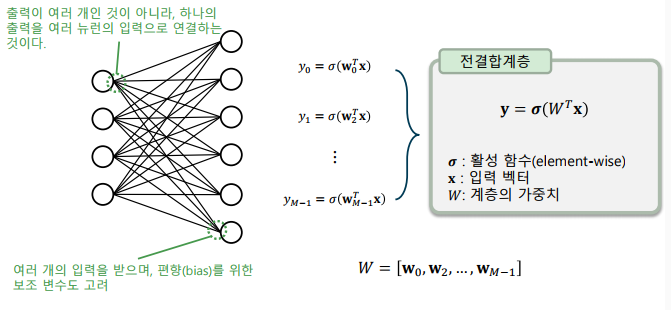
• 전결 합계층
  -> 두 계층 간의 모든 뉴런이 서로 연결되어 있는 구조
  -> 한 계층의 모든 출력과 다음 계층의 모든 입력을 연결
  

인공신경망의 구조

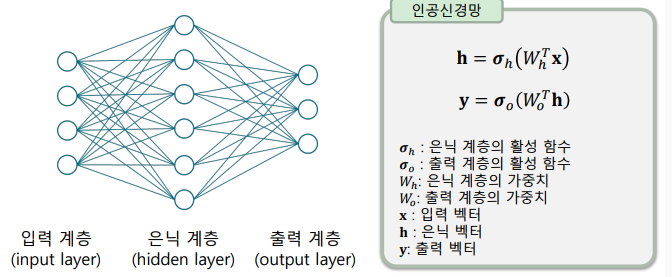
• 인공신경망(ANN): 두 개의 전결합계층을 연결한, 가장 간단한 인공신경망
  -> 입력 계층, 은닉 계층, 출력 계층으로 이루어진 인공신경망 구조
  -> 얕은 신경망(shallow neural network)
  

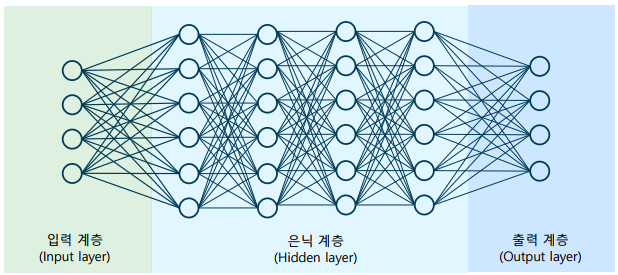
• 심층신경망(DNN): 은닉 계층의 개수를 늘린 인공신경망
  -> 보통 5개 이상의 계층이 있는 경우 깊다고 표현
  

이 글은 제로베이스 데이터 취업 스쿨의 강의 자료 일부를 발췌하여 작성되었습니다