딥러닝 (4)

Chapter 4 최적화 기법

최적화 이론

• 가능한 모든 해 중 최적의 해를 찾는 문제를 해결하는 이론
• 제약 조건(constraint conditions)을 지키면서 목적 함수(objective function)가 최소가 되게 하는 최적의 해(optimal solution)를 찾는 문제
• 최소화 문제와 최대화 문제는 상호 변환 가능
  

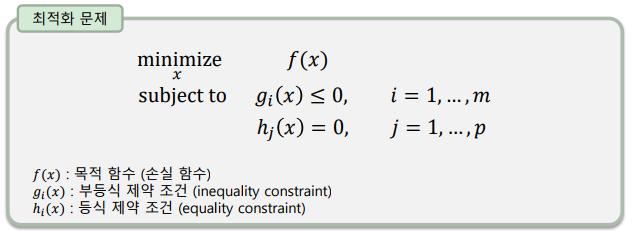
최적화 문제의 풀이

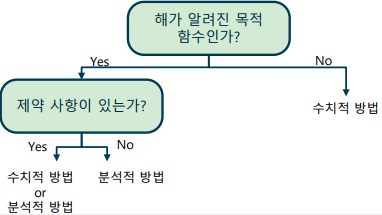
• 목적 함수의 형태와 제약 조건에 따라 다양한 해법이 있음

• 분석적 방법(analytic method) – 함수의 모든 구간의 수식을 알 때 사용하는 수식적인 해석 방법

• 수치적 방법(numerical method) – 함수의 형태와 수식을 알지 못할 때 사용하는 계산적인 해석 방법
  

• 최적화 문제를 해결하는 대표적인 분석적 방법
  -> 다항식 최적화 문제

• 최적화 문제를 해결하는 대표적인 수치적 방법
  -> 이분 탐색
  -> 황금분할 탐색
  -> 경사 하강법 (gradient descent)
  -> 뉴턴의 방법 (이차함수 가정)

전역 최적해와 국소 최적해

• 전역 최적해(global optimal solution)과 국소 최적해(local optimal solution)
  -> 전역 최적해는 정의역(domain)에서 단 하나 존재
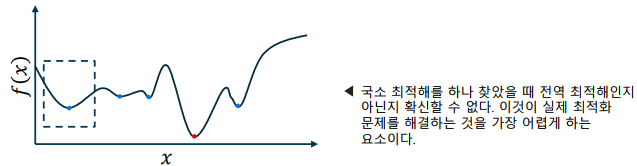
  -> 국소 최적해는 정의역에 여러 개 존재할 수 있음, 함수 개형을 알 수 없는 경우 국소 최적해의 개수는 알 수 없음
  -> 일반적으로 하나의 해를 찾았을 때, 이것이 전역 최적해인지 국소 최적해인지 알 수 있는 방법은 없음
  

딥러닝과 최적화 이론의 관계

• 인공신경망의 매개변수(trainable parameter, weight, bias)를 결정하기 위해 최적화 이론을 사용
  -학습 데이터에 대한 손실 함수를 최소화하는 최적화된 매개변수를 찾는 최적화 문제를 해결
  -임의의(arbitrary) 형태를 가진 목적 함수에 특별한 제약사항이 없으므로, 수치적 방법을 사용. 특히, 미분 기반의 방법을 사용
  

미분과 기울기

• 무차별 대입법(Brute-force): 가능한 모든 수를 대입해서 최적값을 알아내는 최적화 기법으로, 가장 단순한 방법으로 구현할 수 있음
  -> 다음과 같은 이유로 실제 최적화 문제에 이용할 수 없다.
  -> $𝑥^∗$(최적값)이 존재하는 범위를 알아야 함
  -> $𝑥^∗$를 정밀하게 찾기 위해 무한히 촘촘하게 조사해야 함
  -> $𝑓(𝑥)$의 계산 복잡도가 매우 높음
  

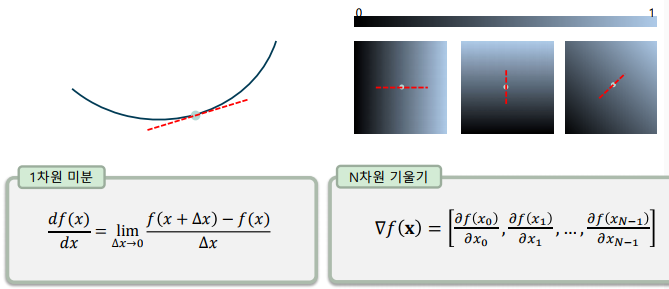
• 1차원 미분과 N차원 기울기(gradient)
  -> 미분은 함수의 접선의 기울기를 의미
  -> 기울기는 여러 매개변수로 각각 편미분한 결과를 이용
  

경사하강법

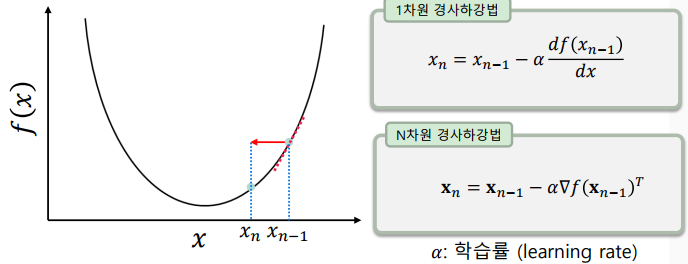
• 함수의 미분을 이용하여 점차적으로 최적값을 찾아나가는 최적화 기법
  -> 미분(기울기)는 함수가 증가하는 방향이므로, 그 반대 방향으로 이동
  -> 더 이상 목적 함수의 값이 변하지 않을 때 까지 스텝을 반복
  

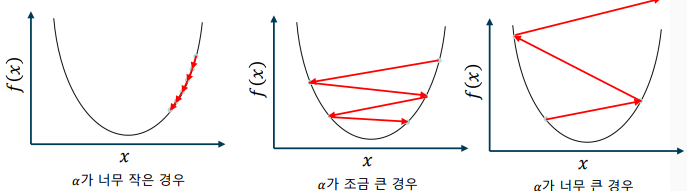
• 학습률에 따른 경사하강법의 동작
  -> 학습률이 너무 작은 경우 – 최적값에 도달하는 데에 너무 많은 스텝 소요
  -> 학습률이 조금 큰 경우 – 최적값에 접근하지 못하고 주변에서 진동
  -> 학습률이 너무 큰 경우 – 최적값에서 오히려 멀어지는 현상 발생
  

다양한 함수와 경사하강법

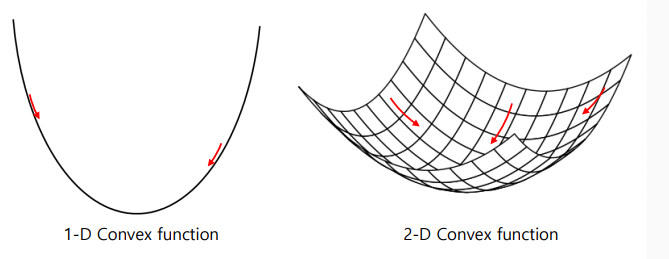
• 볼록함수(convex function): 어디서 시작해도 경사하강법으로 최적값에 도달
  

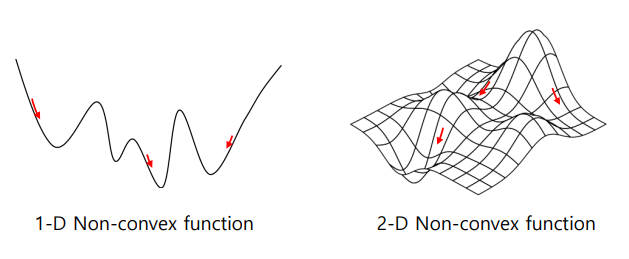
• 비볼록함수(non-convex function): 시작 위치에 따라 다른 국소 최적값을 가짐
  

심화 최적화 기법

• 복잡한 함수의 국소 최적값: 기본 경사하강법을 사용할 경우, 초기값에 따라 국소 최소값에 빠질 위험이 있음
  

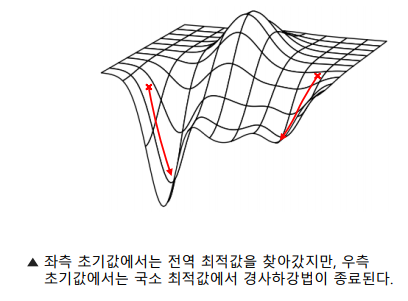
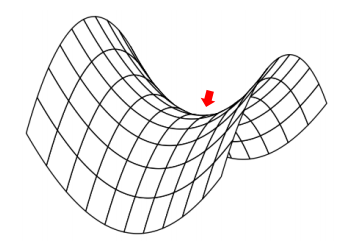
• 안장점과 경사하강법
  -> 안장점(saddle point)은 기울기의 크기가 0이지만, 극값이 아닌 지점
  -> 경사하강법은 안장점에서 기울기가 0이기 때문에 벗어나지 못함
  

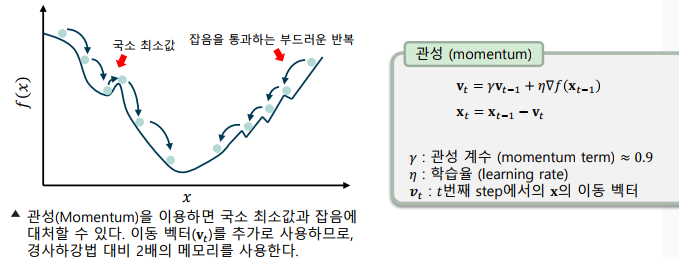
• 관성기법(Momentum)
  -> 이전의 기울기에 영향을 받는 속도 벡터를 사용
  -> 돌이 굴러 떨어지는 것 처럼, 국소 최소값에 도달해도 관성에 의해 계속 진행될 수 있도록 함
  

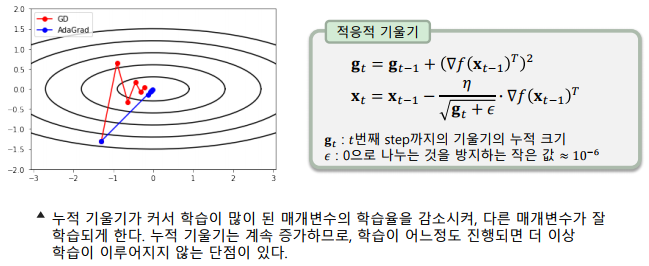
• 적응적 기울기 기법(AdaGrad: Adaptive Gradient)
  -> 변수별로 학습율이 적응적으로 달라지게 조절하는 알고리즘
  -> 적응적(adaptive) – 상황에 맞게 다르게 동작하는 특성
  

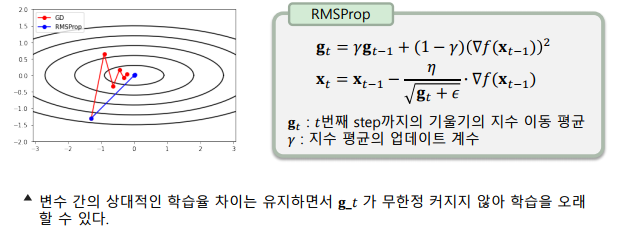
• RMSProp기법
  -> 기울기의 누적합 대신, 기울기의 지수 이동 평균을 이용한다.
  -> AdaGrad의 문제점을 개선한 버전으로, Hinton 교수가 온라인 강의에서 공개
  

• Adam(Adaptive moment estimation) 최적화 기법
  -> RMSProp과 관성 기법을 동시에 적용한 알고리즘
  -> 딥러닝 네트워크를 학습하는 데에 가장 많이 사용되는 기법
  

이 글은 제로베이스 데이터 취업 스쿨의 강의 자료 일부를 발췌하여 작성되었습니다