딥러닝 (5)

Chapter 5 역전파

역전파 알고리즘의 필요성

• 화이트박스 모델과 블랙박스 모델
  -> 화이트박스(white box) – 모델의 동작 원리와 근거를 명확히 파악할 수 있는 모델로, 전통적인 머신 러닝 모델이 이에 해당
  -> 블랙박스(black box) – 모델의 내부 동작을 이해하기 어렵지만, 일반적으로 뛰어난 성능을 낼 수 있는 딥러닝과 같은 모델이 이에 해당

• 블랙박스 모델의 학습
  -> 매개변수 별로 손실 함수를 미분하여, 경사하강법을 수행한다.
  

• 수치적 기울기(Numerical gradient)
  -> 미분의 정의로부터 극한 연산을 근사하여 기울기를 수치적으로 구할 수 있음
  -> 충분히 작은 𝜖𝜖값을 사용하면 손실 함수를 2번 평가하여 미분의 근사값을 알 수 있음
  

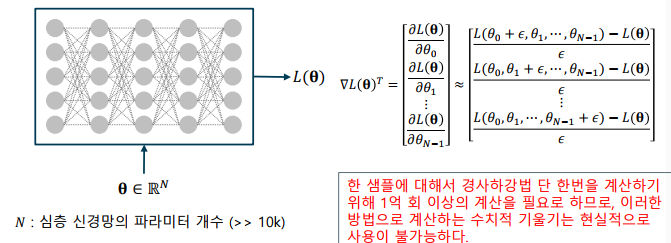
• 심층신경망의 수치적 기울기
  -> 총 N개의 매개변수를 가진 심층신경망의 학습
  -> 1회 손실 함수 평가에 필요한 곱연산의 개수 $≈𝑁$
  -> 미분을 위해 필요한 손실 함수 평가 횟수 $≈𝑁$
  -> 경사하강법 1스텝을 위해 필요한 곱연산의 수 $≈𝑁^2$ ($𝑁$ ≫ 10000)
  

심층신경망과 미분의 연쇄 법칙

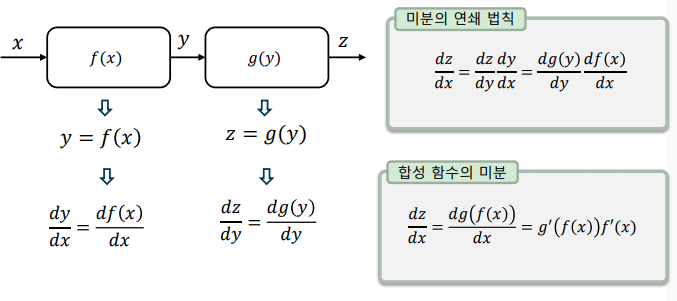
• 미분과 연쇄 법칙: 직렬 연결된(cascade) 함수는 연쇄 법칙(chain rule)로 표현
  -> 합성 함수의 미분(겉미분과 속미분의 곱)과 동일
  

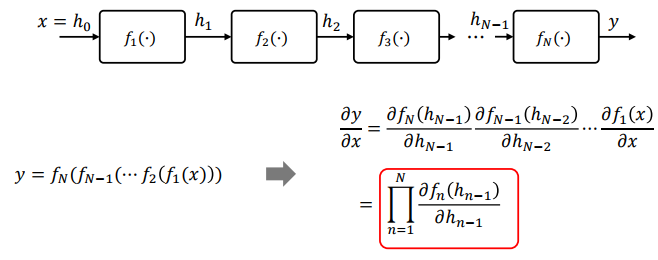
• 연쇄 법칙의 확장: 함수의 직렬 연결이 계속되면, 연쇄 법칙을 연속으로 사용할 수 있음
  

• 심층신경망의 함성 함수 표현: 심층신경망의 각 계층을 함수로 치환하면, 입출력 관계를 하나의 합성 함수로 바꾸어 표현할 수 있음
  

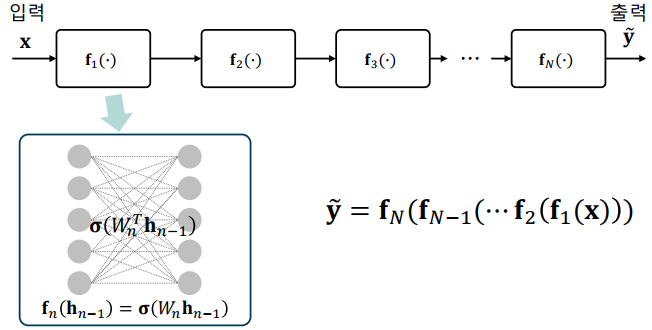
• 심층신경망의 매개변수 학습(미분 계산)
  -> 심층신경망을 학습할 때에는, 입력과 출력보다는 손실 함수와 매개변수가 주 변수가 됨
  -> 신경망의 입력과 출력은 손실 함수와 그 미분을 평가하기 위해서
  사용
  

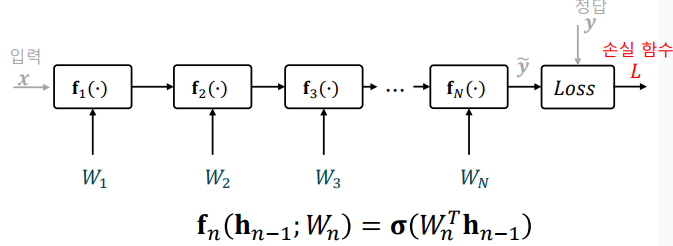
• 심층신경망 손실 함수의 미분: 매개변수별로 미분을 계산할 때에는 연쇄법칙을 사용
  -> 미분하고자 하는 경로 사이에 있는 모든 미분을 곱함
  

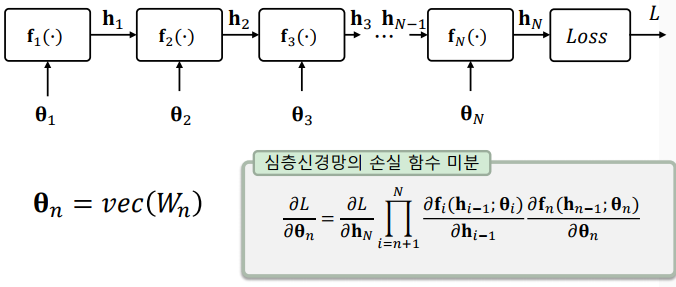
손실함수의 미분

• 심층신경망의 미분
  -> 심층신경망을 미분하기 위해 필요한 요소
  -> 예측치로 미분한 손실 함수
  -> 입력으로 미분한 각 계층의 출력
  -> 매개변수로 미분한 각 계층의 출력
  

• 손실함수의 미분: 손실함수는 보통 미분이 용이한 함수로 선택
  -> 제곱, 로그함수, 지수 함수 등을 사용하여 미분이 용이
  

전결합 계층의 미분

• 활성 함수의 미분과 행렬 곱의 미분의 곱으로 이루어짐
  -> 활성 함수의 미분은 정방향 연산 과정에서 계산 가능
  -> 입력/가중치 편미분은 선형 함수이므로 계산이 불필요
  

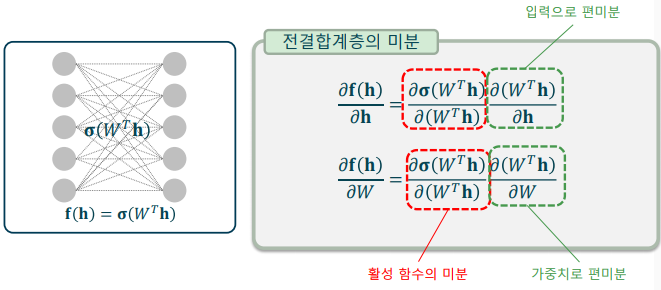
활성함수의 미분

• 함수의 출력을 이용해 계산할 수 있는 특징이 있음
  

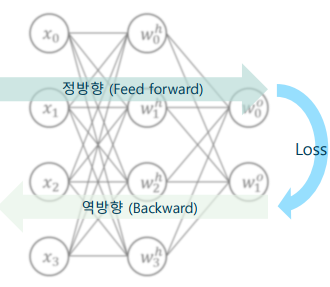
역전파 알고리즘

• 역전파 알고리즘을 이용하면 손실함수를 단 한번 평가하여 미분을 구할 수 있음
• 오류 역전파 알고리즘(BP: Backpropagation Algorithm)
  -> 학습 데이터로 정방향 연산을 하여 손실 함수 출력을 구함
  -> 정방향 연산 시, 계층별로 BP에 필요한 중간 결과를 저장
  -> 손실 함수를 각 매개변수로 미분, 연쇄법칙(역방향 연산)을 이용
  -> 마지막 계층부터 하나씩 이전 계층으로 연쇄적으로 계산
  -> 역방향 연산 시, 정방향 연산에서 저장한 중간 결과를 사용
  

기울기 소실 문제와 해결

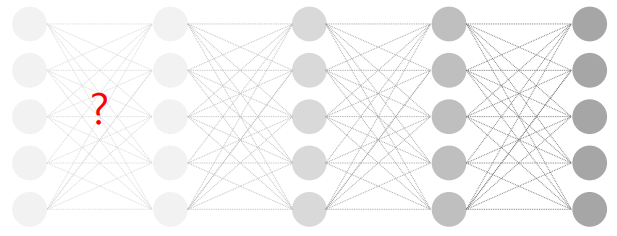
• 역전파 학습의 한계: 기울기 소실 문제 (Vanishing gradient)
  -> 계층이 많아지면, 출력에서 먼 계층이 학습되지 않는 현상
  -> 역전파 알고리즘은 80년대에 개발되었으나, 기울기 소실 문제로 많은 계층을 학습해내지 못함
  

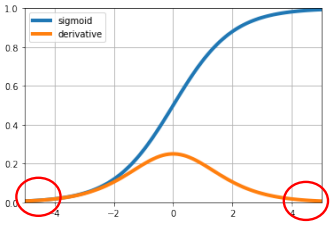
• 기울기 소실의 원인: 활성 함수가 거듭 곱해지면서 발생
  -> 당시 많이 사용되던 시그모이드 활성 함수의 미분값이 매우 작음
  -> 역전파 과정에서 시그모이드 함수가 거듭 곱해지면서 기울기가 급격히 감소
  -> 여러 계층에서 중앙에서 벗어난 값이 발생할 경우, 연쇄 법칙에 의해 기울기의 크기가 급격히 감소해 학습이 거의 이루어지지 않음
  

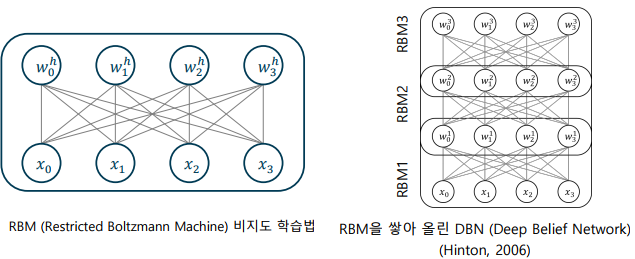
• 심층 믿음 신경망(DBN: Deep Belief Network)
  -> 2006년 제안된 제한 볼츠만 머신(restricted Boltzmann machine)을 이용한 사전 학습 방법
  -> 심층신경망의 초기값을 개선하여 기울기가 작아지지 않도록 유도
  

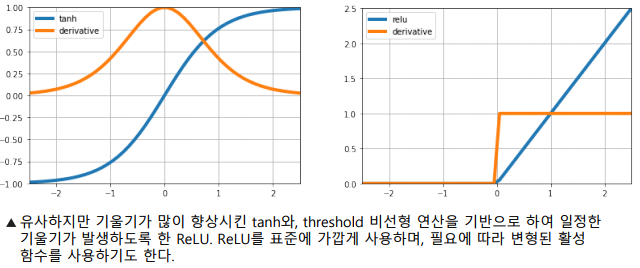
• 활성함수의 개선
  -> tanh를 이용해 기울기를 향상시키기 위한 노력
  -> ReLU의 등장으로 기울기가 대폭 향상되었으며, 표준처럼 사용
  

Chapter 6 인공신경망의 학습

미니 배치 학습법

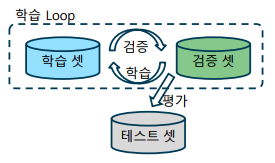
• 대규모 데이터셋을 이용한 학습: 대규모 데이터셋은 학습, 검증, 테스트 데이터셋으로 이루어짐
  -> 학습 데이터(training data) – 학습 과정에서 실제 모델을 학습하는 데에 사용되는 데이터
  -> 검증 데이터(validation data) – 학습 과정에서 학습이 잘 되고 있는지 검증하는 데에 사용되는 데이터
  -> 테스트 데이터(test data) – 학습을 마친 모델을 평가하기 위해사용하는 데이터

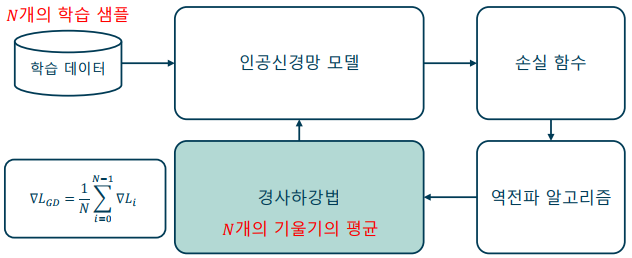
• 기본 경사하강법(GD: Vanilla Gradient Descent): 매개변수를 한번 업데이트하기 할 때마다 매번 모든 학습 데이터를 사용
  

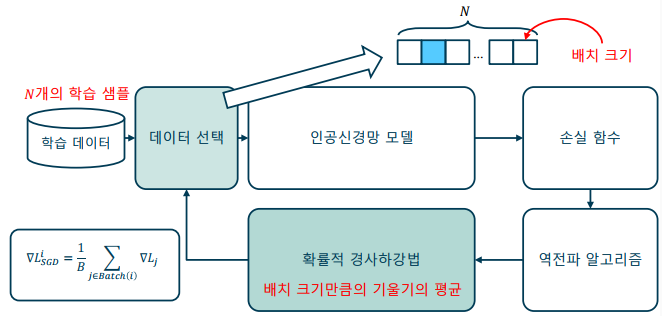
• 확률적 경사하강법(SGD: Stochastic Gradient Descent): 매개변수를 한번 업데이트하기 할 때마다 정해진 배치 크기 만큼의 데이터만을 사용
  

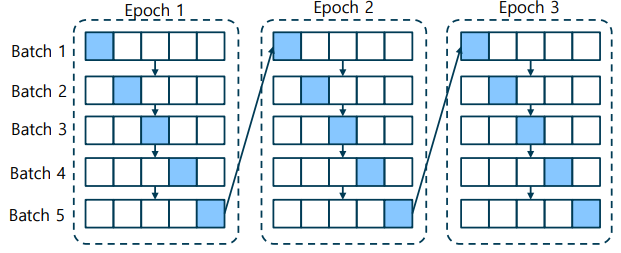
• 미니 배치 학습법: 학습 데이터를 일정한 크기로 나누어 학습하는 기법
  -> 에포크(epoch) - 학습 데이터 전체를 한번 학습 하는 것
  -> 배치(batch, mini-batch) – 학습의 한 스텝을 업데이트하는 단위
  

인공신경망 학습의 구현

import tensorflow as tf

mnist = tf.keras.datasets.mnist
(X, y), _ = mnist.load_data()  # we only use trainig set from original dataset
X = X / 255.0  # input range from [0, 255] to [0.0, 1.0]
total_dataset = tf.data.Dataset.from_tensor_slices((X, y))

# train_set(35%), valid_set(15%), test_set(50%)
num_train = len(total_dataset) * 35 // 100
num_valid = len(total_dataset) * 15 // 100
num_test = len(total_dataset) - num_train - num_valid

# take(x): use next x samples
# skip(x): skip next x samples
train_dataset = total_dataset.take(num_train).shuffle(1024, reshuffle_each_iteration=True).batch(32)
valid_dataset = total_dataset.skip(num_train).take(num_valid).batch(128)
test_dataset = total_dataset.skip(num_train).skip(num_valid).batch(128)

# take(x): use next x samples
# skip(x): skip next x samples
train_dataset = total_dataset.take(num_train).shuffle(1024, reshuffle_each_iteration=True).batch(32)
valid_dataset = total_dataset.skip(num_train).take(num_valid).batch(128)
test_dataset = total_dataset.skip(num_train).skip(num_valid).batch(128)

class Model(tf.keras.Model):
    def __init__(self):  # defines variables and layers
        super().__init__()
        self.flatten = tf.keras.layers.Flatten()
        self.dense1 = tf.keras.layers.Dense(32, activation='relu')
        self.dense2 = tf.keras.layers.Dense(64, activation='relu')
        self.dense3 = tf.keras.layers.Dense(128, activation='relu')
        self.dense4 = tf.keras.layers.Dense(10, activation='softmax')
    
    def call(self, x):  # defines feed-forward operation
        x = self.flatten(x)
        x = self.dense1(x)
        x = self.dense2(x)
        x = self.dense3(x)
        return self.dense4(x)
        
def loss_func(y_true, y_pred):  # CEE loss for multi-class classification
    return tf.losses.sparse_categorical_crossentropy(y_true, y_pred)
    
@tf.function
def train_step(model, X, y, optimizer, train_loss, train_accuracy):
    with tf.GradientTape() as t:  # calculate gradients
        y_pred = model(X)
        loss = loss_func(y, y_pred)
    grads = t.gradient(loss, model.trainable_weights)               # get gradients
    optimizer.apply_gradients(zip(grads, model.trainable_weights))  # apply gradients

    train_loss(loss)           # collect loss for averaging
    train_accuracy(y, y_pred)  # collect accuracy for averaging
    
@tf.function
def valid_step(model, X, y, valid_loss, valid_accuracy):
    y_pred = model(X)
    loss = loss_func(y, y_pred)

    valid_loss(loss)           # collect valid loss for averaging
    valid_accuracy(y, y_pred)  # collect valid accuracy for averaging
    
model = Model()
optimizer = tf.optimizers.SGD(0.01)

train_loss = tf.keras.metrics.Mean(name='train_loss')
train_accuracy = tf.keras.metrics.SparseCategoricalAccuracy(name='train_accuracy')
valid_loss = tf.keras.metrics.Mean(name='valid_loss')
valid_accuracy = tf.keras.metrics.SparseCategoricalAccuracy(name='valid_accuracy')
test_accuracy = tf.keras.metrics.SparseCategoricalAccuracy(name='test_accuracy')

for epoch in range(20):
    for X_batch, y_batch in train_dataset:
        train_step(model, X_batch, y_batch, optimizer, train_loss, train_accuracy)

    for X_batch, y_batch in valid_dataset:
        valid_step(model, X_batch, y_batch, valid_loss, valid_accuracy)
    
    print('epoch{}: train_loss:{}, train_acc:{}, valid_loss:{}, valid_acc:{}'.format(
        epoch+1, train_loss.result(), train_accuracy.result()*100, valid_loss.result(), valid_accuracy.result()*100
    ))

    train_loss.reset_state()
    train_accuracy.reset_state()
    valid_loss.reset_state()
    valid_accuracy.reset_state()
    
for X_batch, y_batch in test_dataset:
    y_pred = model(X_batch)
    test_accuracy(y_batch, y_pred)
print('test result: {}'.format(test_accuracy.result()*100))
test_accuracy.reset_state()

이 글은 제로베이스 데이터 취업 스쿨의 강의 자료 일부를 발췌하여 작성되었습니다