머신러닝 (10)

Chapter 15 주성분 분석

• PCA: 정보를 최대한 보존하면서 새로운 축을 찾아, 고차원을 저차원으로 변환

• 차원축소와 변수추출 기법으로 많이 쓰이는 주성분 분석

• 데이터를 어떤 벡터에 정사영시켜 차원을 낮출 수 있음
  

• 새로운 특성을 찾아서 표현하는 것

from sklearn.decomposition import PCA

pca = PCA(n_components=2, random_state=13) # 주성분을 2개만 찾아라
pca.fit(X) 

def draw_vector(v0, v1, ax=None): 
    ax = ax or plt.gca() 
    arrowprops = dict(arrowstyle='->', linewidth=2, color='black', shrinkA=0, shrinkB=0) 
    ax.annotate('', v1, v0, arrowprops=arrowprops) 

plt.scatter(X[:, 0], X[:, 1], alpha=0.4) 

for length, vector in zip(pca.explained_variance_, pca.components_): 
    v = vector * 3 * np.sqrt(length) 
    draw_vector(pca.mean_, pca.mean_ + v)

plt.axis('equal');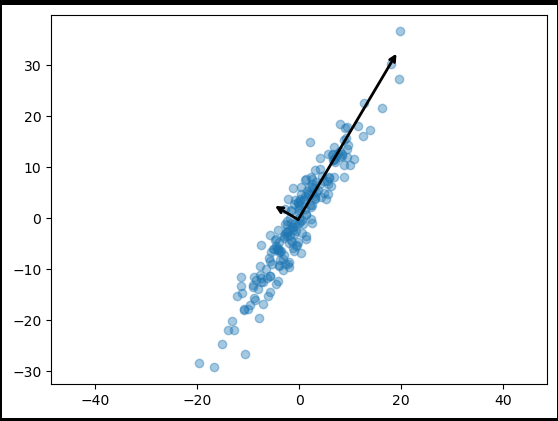

pca = PCA(n_components=1, random_state=13) 
pca.fit(X) 
X_pca = pca.transform(X) 

pca.explained_variance_ratio_

X_new = pca.inverse_transform(X_pca) 

plt.scatter(X[:, 0], X[:, 1], alpha=0.4) 
plt.scatter(X_new[:, 0], X_new[:, 1], alpha=0.8) 
plt.axis('equal');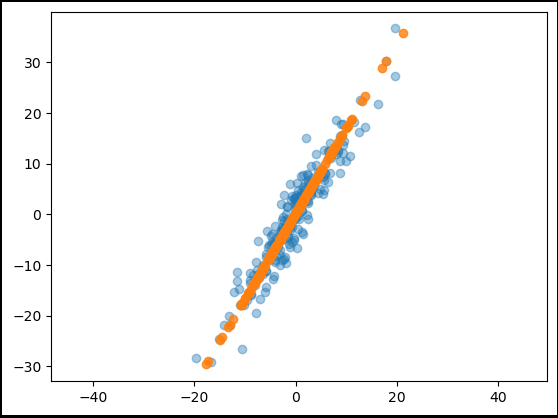

Iris 데이터에 PCA 적용

import pandas as pd 
from sklearn.datasets import load_iris 

iris = load_iris() 

iris_pd = pd.DataFrame(iris.data, columns=iris.feature_names) 
iris_pd['species'] = iris.target 
iris_pd.head()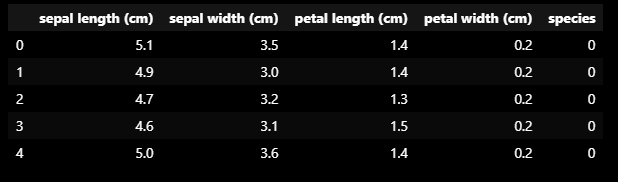

• Iris 데이터는 특성이 4개라 한번에 그릴 수 없음

from sklearn.preprocessing import StandardScaler 

iris_ss = StandardScaler().fit_transform(iris.data) 
iris_ss[:5]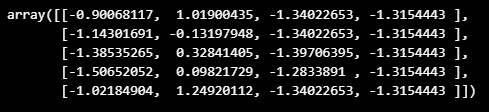

from sklearn.decomposition import PCA 

def get_pca_data(ss_data, n_components=2): 
    pca = PCA(n_components=n_components) 
    pca.fit(ss_data) 

    return pca.transform(ss_data), pca 

iris_pca, pca = get_pca_data(iris_ss, 2) 
iris_pca.shape

(150, 2)

pca.mean_

array([-1.69031455e-15, -1.84297022e-15, -1.69864123e-15, -1.40924309e-15])

pca.components_ 

array([[ 0.52106591, -0.26934744, 0.5804131 , 0.56485654],
[ 0.37741762, 0.92329566, 0.02449161, 0.06694199]])

def get_pd_from_pca(pca_data, cols=['PC1', 'PC2']): 
    return pd.DataFrame(pca_data, columns=cols) 
    
iris_pd_pca = get_pd_from_pca(iris_pca) 
iris_pd_pca['species'] = iris.target 
iris_pd_pca.head()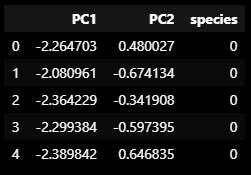    

sns.pairplot(iris_pd_pca, hue='species');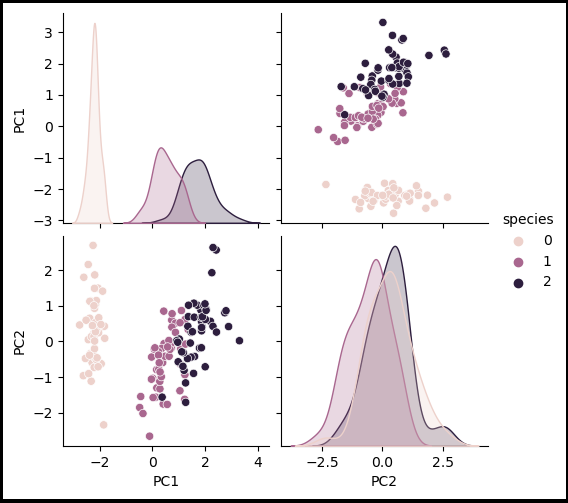 

def print_variance_ratio(pca): 
    print('Explained variance ratio: {}'.format(pca.explained_variance_ratio_)) 
    print('Cumulative explained variance ratio: {}'.format(np.cumsum(pca.explained_variance_ratio_))) 
    
print_variance_ratio(pca) 

Explained variance ratio: [0.72962445 0.22850762]
Cumulative explained variance ratio: [0.72962445 0.95813207]

와인 데이터에 PCA 적용

wine_ss = StandardScaler().fit_transform(wine_X) 

pca_wine, pca = get_pca_data(wine_ss, 2) 
pca_wine.shape 

(6497, 2)

print_variance_ratio(pca) 

Explained variance ratio: [0.25346226 0.22082117]
Cumulative explained variance ratio: [0.25346226 0.47428343]

pca_columns = ['PC1', 'PC2'] 
pca_wine_pd = get_pd_from_pca(pca_wine, pca_columns) 
pca_wine_pd['color'] = wine_y.values 

sns.pairplot(pca_wine_pd, hue='color');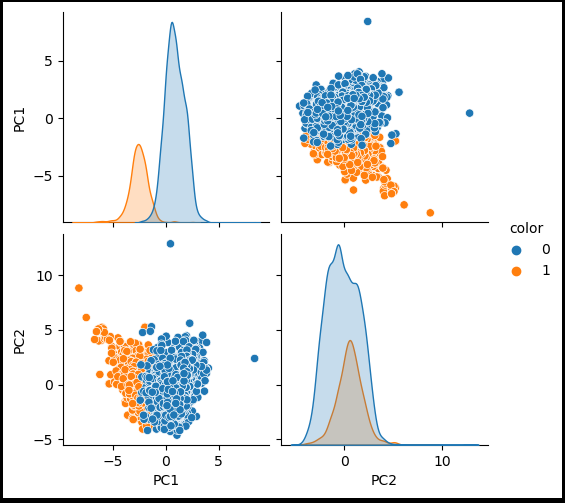 

pca_wine, pca = get_pca_data(wine_ss, 3) 
print_variance_ratio(pca) 

Explained variance ratio: [0.25346226 0.22082117 0.13679223]
Cumulative explained variance ratio: [0.25346226 0.47428343 0.61107566]

import plotly.express as px 

fig = px.scatter_3d(pca_wine_plot, x='PC1', y='PC2', z='PC3', color='color') 
fig.update_layout(margin=dict(l=0, r=0, b=0, t=0)) 
fig.show()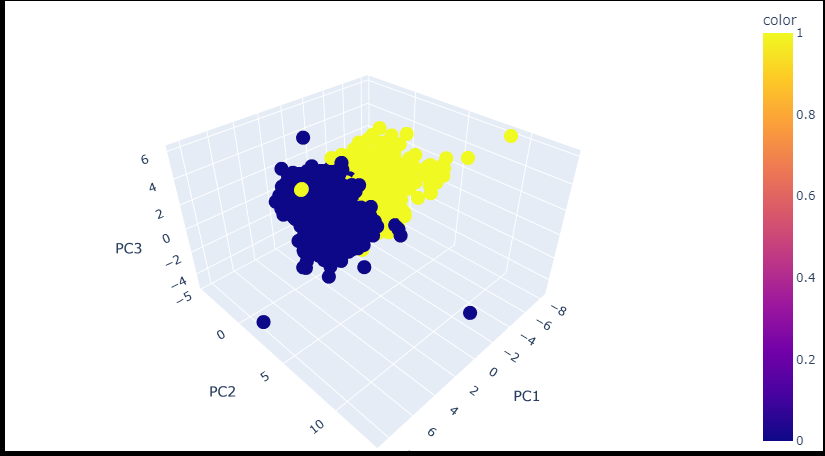 

• 주성분 분석은 데이터를 시각화 하는 부분에도 도움을 줌

이 글은 제로베이스 데이터 취업 스쿨의 강의 자료 일부를 발췌하여 작성되었습니다