머신러닝 (2)

Chapter3 (회귀)

1. 지도 학습과 비지도 학습

• 머신러닝의 종류: 지도학습, 비지도학습, 강화학습
• 지도학습: 정답을 알려주고 학습시키는 것
  1) 분류 Classification (0/1 방식으로 구분되는 것)

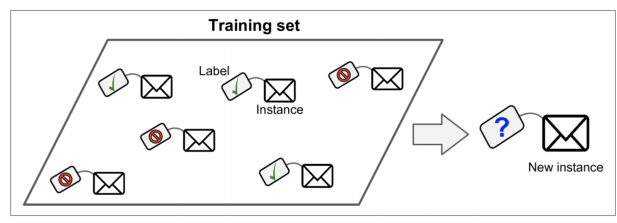
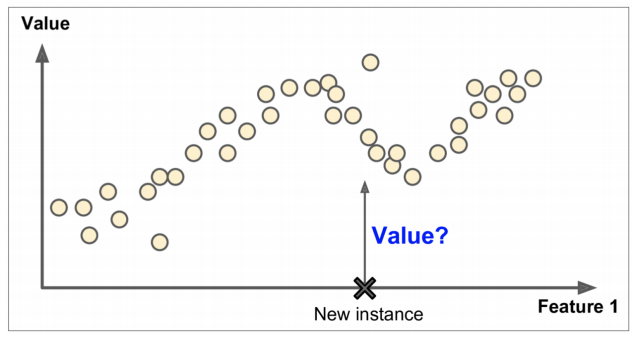
2) 회귀 Regression (정답, 라벨이 연속적인것)

• 비지도학습: 정답이 없고, 특성만 가지고 학습하는 것
  1) 군집
  

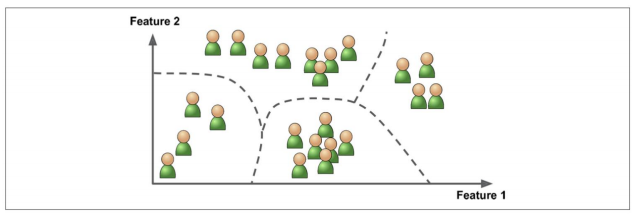
2) 차원 축소

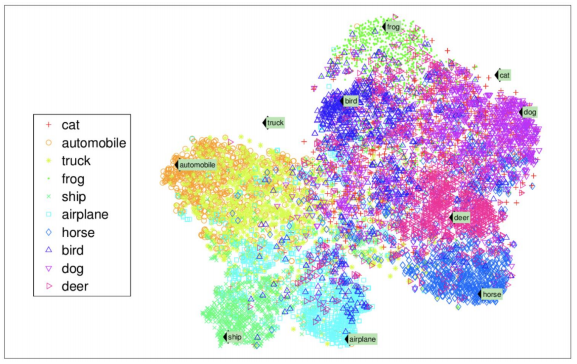
2. 회귀 (Regression)

• 학습 데이터 각각에 정답이 주어져 있고, 연속된 값으로 예측하면 지도학습 회귀

3. 선형회귀 (Linear Regression)

• 입력 변수 x가 하나인 경우, 선형 회귀 문제는 주어진 학습데이터와 가장 잘 맞는 Hypothesis 함수 h를 찾는 문제가 됨

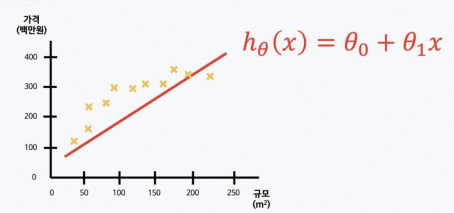
• 실습

import pandas as pd

data = {'x' : [1., 2., 3., 4., 5.], 'y' : [1., 3., 4., 6., 5.]}
df = pd.DataFrame(data)
df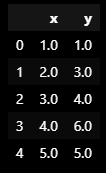

import matplotlib.pyplot as plt

plt.scatter(df['x'], df['y'])
plt.grid()
plt.show()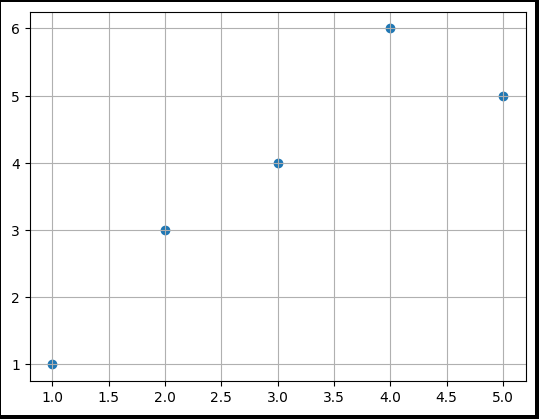

from sklearn.linear_model import LinearRegression

X = df[['x']]
y = df['y']

reg = LinearRegression()
reg.fit(X, y)

import numpy as np
from sklearn.metrics import mean_absolute_error

pred = reg.predict(X)
mae = (np.sqrt(mean_absolute_error(y, pred)))
mae

plt.scatter(y, pred)
plt.xlabel("Actual")
plt.ylabel("Predicted")
plt.title("Real vs Predicted")
plt.plot([0, 6], [0, 6], 'r')
plt.grid()
plt.show()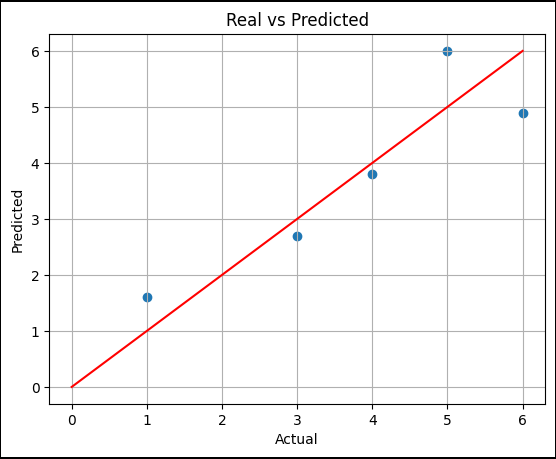

Chapter4 (회귀_보스턴 집 값 예측)

• 여러 개의 특성: 변수가 여러개 있다 Multivariate Linear Regression 문제로 일반화

• 행렬식으로 표현(입력 변수가 4개인 경우)

-> 벡터의 선형회귀 문제로 변환 가능

from pandas import read_csv

column_names = ['CRIM', 'ZN', 'INDUS', 'CHAS', 'NOX', 'RM', 'AGE', 'DIS', 'RAD', 'TAX',
                'PTRATIO', 'B', 'LSTAT', 'PRICE']

url = 'data 주소'

boston_pd = read_csv(url, header=None, delimiter=r"\s+", names=column_names)
boston_pd.head()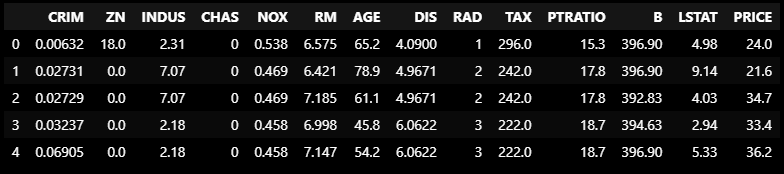

import plotly.express as px

fig = px.histogram(boston_pd, x = "PRICE")
fig.show()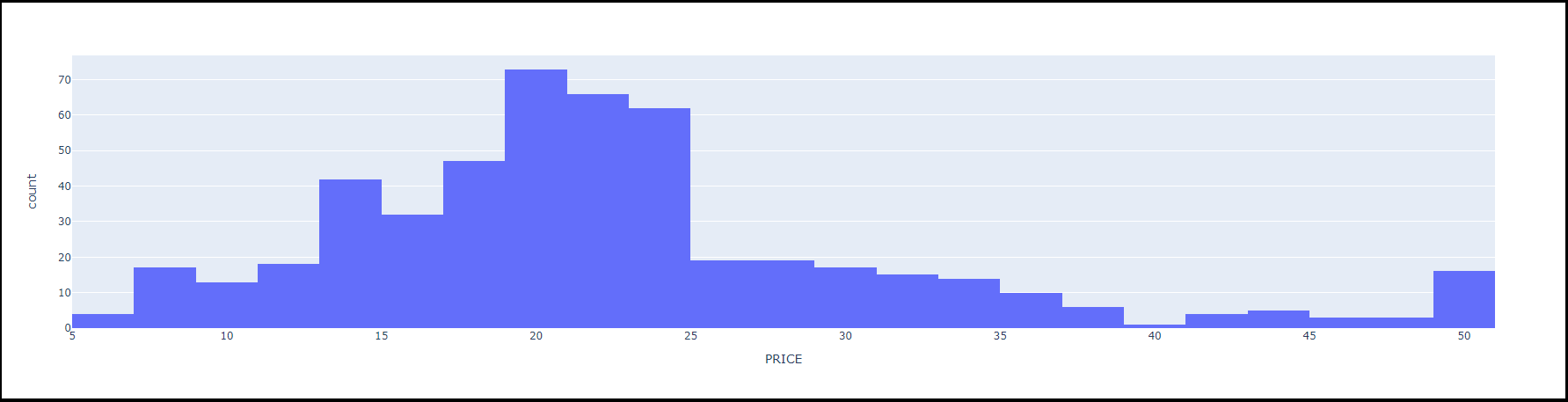

import matplotlib.pyplot as plt
import seaborn as sns

corr_mat = boston_pd.corr().round(1)
sns.set(rc = {'figure.figsize' : (10, 8)})
sns.heatmap(data = corr_mat, annot = True, cmap = 'bwr');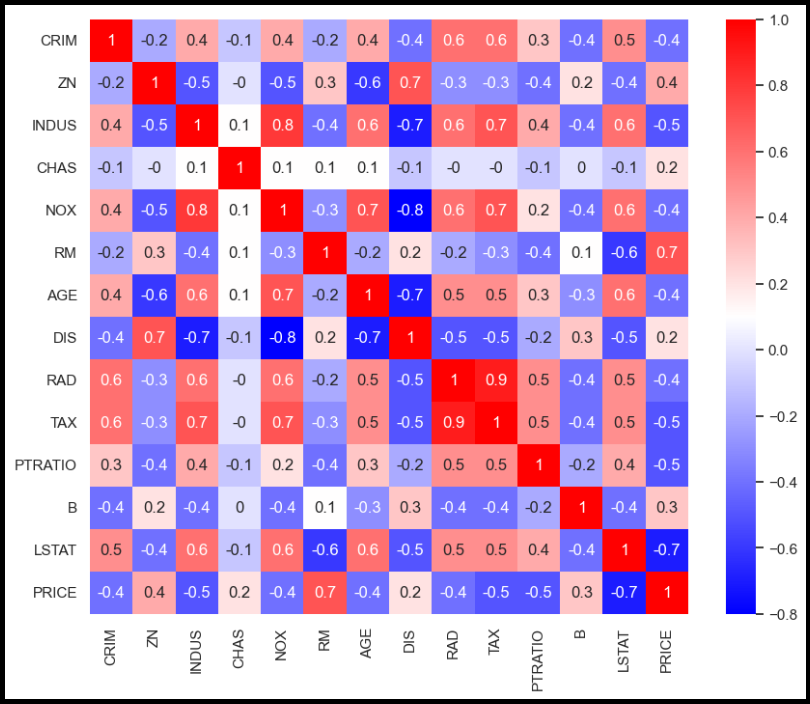

sns.set_style('darkgrid')
sns.set(rc = {'figure.figsize' : (12, 6)})
fig, ax = plt.subplots(ncols = 2)
sns.regplot(x = "RM", y = "PRICE", data = boston_pd, ax = ax[0]);
sns.regplot(x = "LSTAT", y = 'PRICE' , data = boston_pd, ax = ax[1]);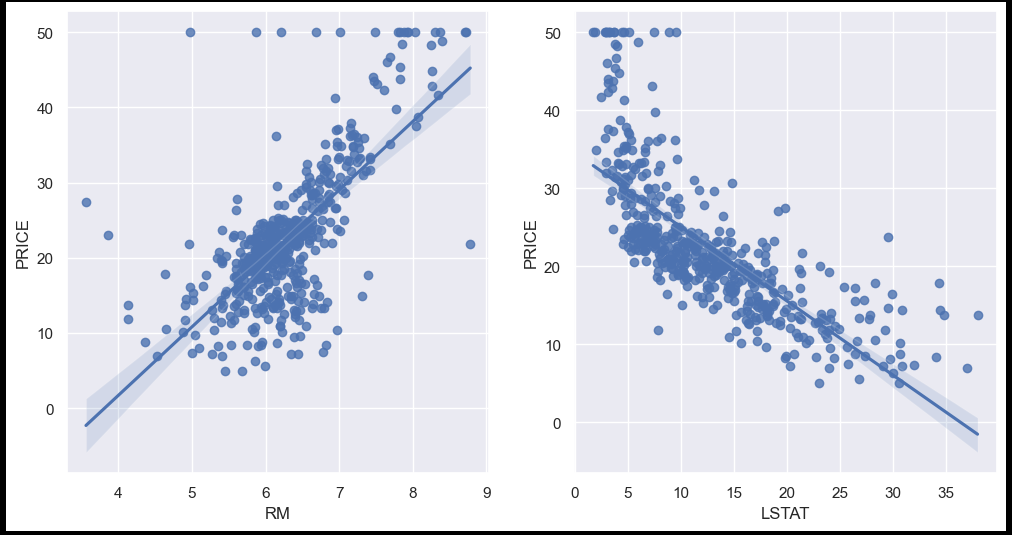

from sklearn.model_selection import train_test_split

X = boston_pd.drop("PRICE", axis = 1)
y = boston_pd["PRICE"]

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.2, random_state = 13)

from sklearn.linear_model import LinearRegression

reg = LinearRegression()
reg.fit(X_train, y_train)

import numpy as np
from sklearn.metrics import mean_squared_error

pred_tr = reg.predict(X_train)
pred_test = reg.predict(X_test)
rmse_tr = (np.sqrt(mean_squared_error(y_train, pred_tr)))
rmse_test = (np.sqrt(mean_squared_error(y_test, pred_test)))

print("RMSE of Train Data : ", rmse_tr)
print("RMSE of Test Data : ", rmse_test)

RMSE of Train Data : 4.642806069019824
RMSE of Test Data : 4.931352584146697

plt.scatter(y_test, pred_test)
plt.xlabel("Actual House Prices ($1000)")
plt.ylabel("Predicted Prices")
plt.title("Real vs Predicted")
plt.plot([0, 48], [0, 48], 'r')
plt.show()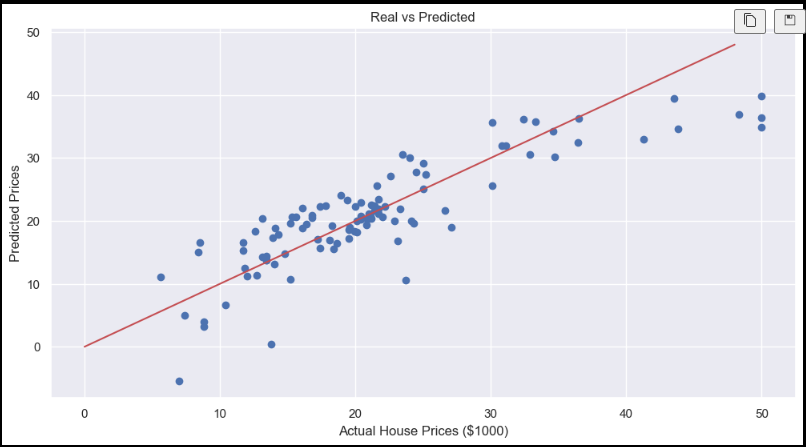

X = boston_pd.drop(["PRICE", "LSTAT"], axis = 1)
y = boston_pd["PRICE"]

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.2,
                                                   random_state = 13)
reg = LinearRegression()
reg.fit(X_train, y_train)

pred_tr = reg.predict(X_train)
pred_test = reg.predict(X_test)
rmse_tr = (np.sqrt(mean_squared_error(y_train, pred_tr)))
rmse_test = (np.sqrt(mean_squared_error(y_test, pred_test)))

print("RMSE of Train Data : ", rmse_tr)
print("RMSE of Test Data : ", rmse_test)

RMSE of Train Data : 5.165137874244863
RMSE of Test Data : 5.295595032597148

plt.scatter(y_test, pred_test)
plt.xlabel("Actual House Prices ($1000)")
plt.ylabel("Predicted Prices")
plt.title("Real vs Predicted")
plt.plot([0, 48], [0, 48], 'r')
plt.show()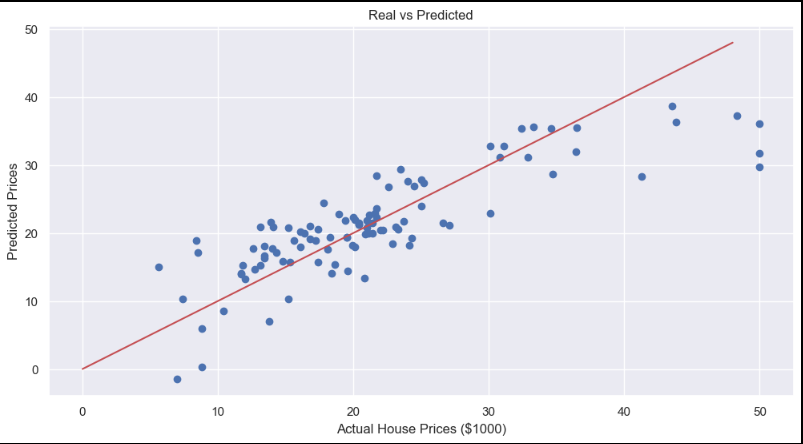

from sklearn.tree import DecisionTreeRegressor

reg_dt = DecisionTreeRegressor(max_depth = 9, random_state = 13)
reg_dt.fit(X_train, y_train)
y_pred_dt = reg_dt.predict(X_test)
rmse_test = (np.sqrt(mean_squared_error(y_test, y_pred_dt)))

print("RMSE of Test Data : ", rmse_test)

RMSE of Test Data : 6.473200592640149

from sklearn import tree

fig = plt.figure(figsize=(15, 8))
_ = tree.plot_tree(reg_dt,feature_names=column_names, filled=True)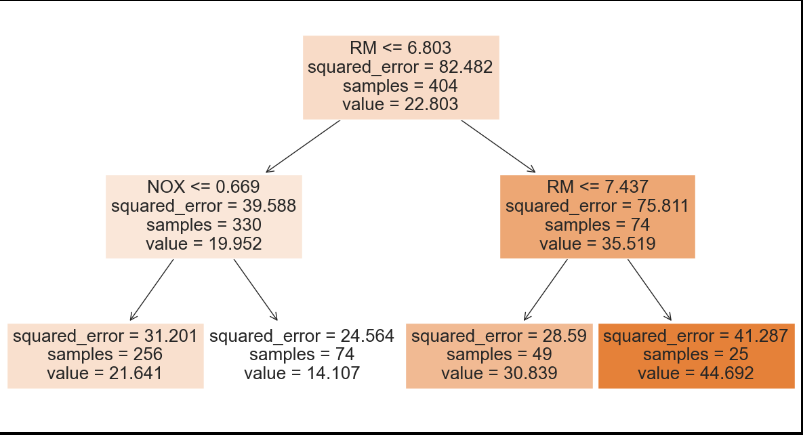

plt.scatter(y_test, y_pred_dt)
plt.xlabel("Actual House Prices ($1000)")
plt.ylabel("Predicted Prices")
plt.title("Real vs Predicted")
plt.plot([0, 48], [0, 48], 'r')
plt.show()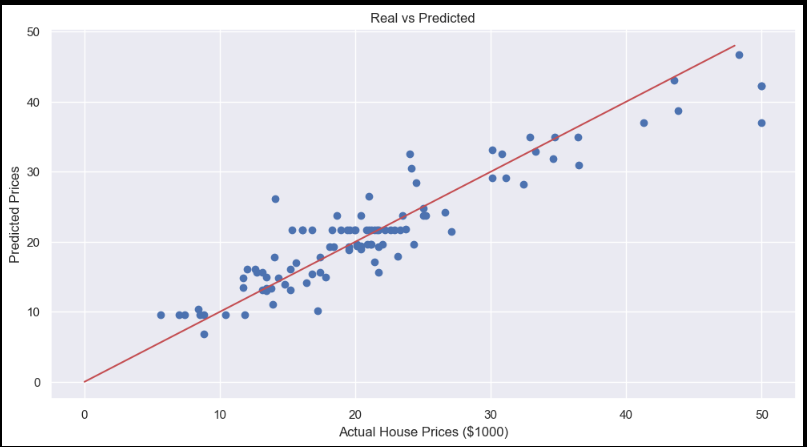

이 글은 제로베이스 데이터 취업 스쿨의 강의 자료 일부를 발췌하여 작성되었습니다