머신러닝 (5)

Chapter 7 분류 모델의 평가

분류 모델 평가

• 모델 자체를 좋다/나쁘다로 평가할 방법은 없음

• 대부분 다양한 모델, 파라미터를 두고 상대적으로 비교

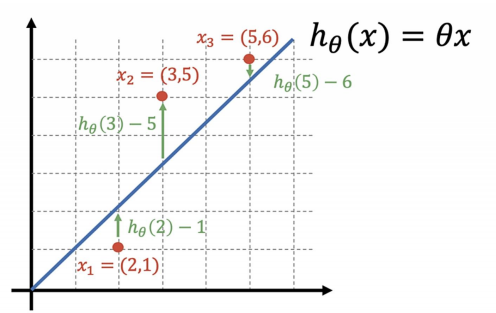
• 회귀 모델은 실제 값과의 에러치를 가지고 계산함
  

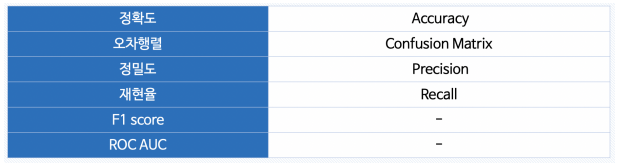
• 분류 모델은 평가 항목이 많음
  

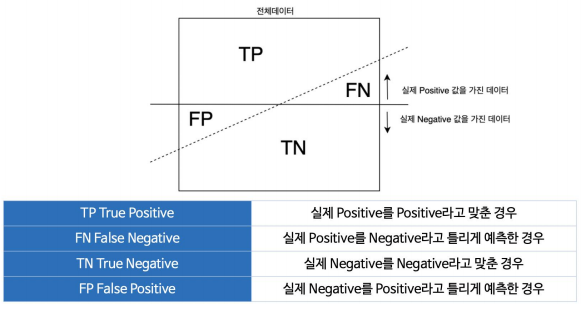
• 이진 분류 모델 평가
  

• Accuracy 정확도: 전체 데이터 중 맞게 예측한 것 비율

  $\text{accuracy} = \frac{TP + TN}{TP + TN + FP + FN}$

• Precision 정밀도: 양성이라고 예측한 것 중 실제 양성 비율

  $\text{precision} = \frac{TP}{TP + FP}$

• Recall 재현율: 참인 데이터 중에서 참이라고 예측한 것

  $\text{recall} = \frac{TP}{TP + FN}$

• Fall-out (FPR): 실제 양성이 아닌데, 양성이라고 잘못 예측한 경우

  $\text{fallout} = \frac{FP}{FP + TN}$

• 분류 모델은 그 결과가 속할 비율(확률)을 반환함
  -> Threshold(임계값)에 따라 Recall, Precision, Fall-out, Accuracy가 달라짐

• Recall은 실제 1 중에서 1을 정확하게 맞추어야 할때 (ex. 의료 분야..)
  -> 실제 양성인 데이터를 음성으로 판단하면 안되므로 Threshold를 0.3, 0.4로 선정

• Precision은 중요한 메일을 놓치면 안되는 상황 등에서 사용 (ex. 스팸메일..)
  -> 실제 음성인 데이터를 양성이라고 판단하면 안되므로 Threshold를 0.8, 0.9로 선정

• F1-Score: Recall과 Precision을 결합한 지표로 어느 한쪽으로 치우치지 않고 둘다 높은 값을 가질 수록 높은 값을 가짐

  $F_{\beta} = (1 + \beta^2) \frac{(\text{precision} \times \text{recall})}{(\beta^2 \cdot \text{precision} + \text{recall})}$
  $F_1 = 2 \cdot \frac{\text{precision} \cdot \text{recall}}{\text{precision} + \text{recall}}$

# ex)
from sklearn.metrics import accuracy_score, precision_score, recall_score, recall_score, f1_score, roc_auc_score, roc_curve

print("accuracy_score", accuracy_score(y_test, y_pred_test))
print("recall_score", recall_score(y_test, y_pred_test))
print("precision_score", precision_score(y_test, y_pred_test))
print("roc_auc_score", roc_auc_score(y_test, y_pred_test))
print("f1_score", f1_score(y_test, y_pred_test))

# result
accuracy_score 0.7276923076923076
recall_score 0.7849331713244229
precision_score 0.7849331713244229
roc_auc_score 0.706931994467243
f1_score 0.7849331713244229

ROC, AUC

• ROC 곡선: 다양한 threshold에 대한 이진분류기의 성능을 한 번에 표시한 것
  

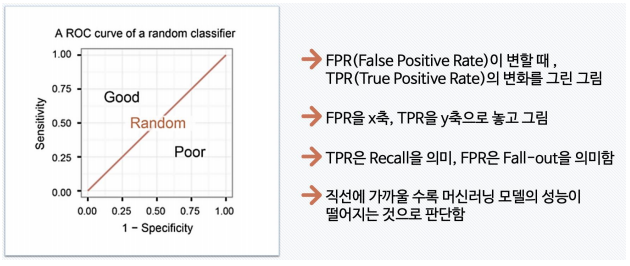
-> 완벽한 분류

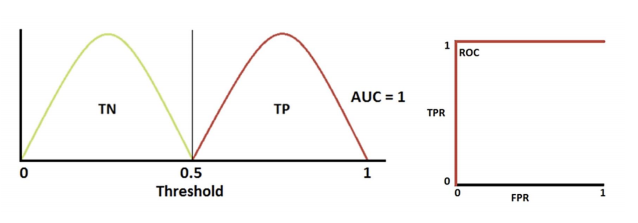
-> 적당한 분류

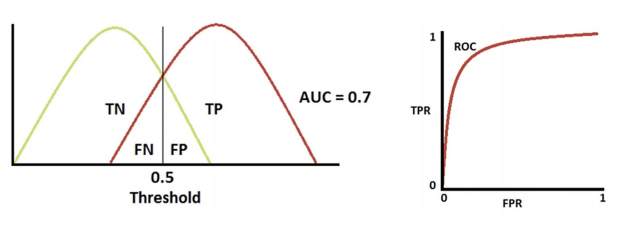
-> 분류 성능이 나쁨

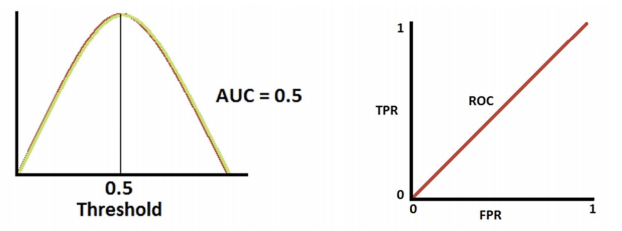
• AUC: ROC 곡선 아래의 면적으로 일반적으로 1에 가까울 수록 좋은 수치

import matplotlib.pyplot as plt 

pred_proba = wine_tree.predict_proba(X_test)[:, 1]
fpr, tpr, _ = roc_curve(y_test, pred_proba)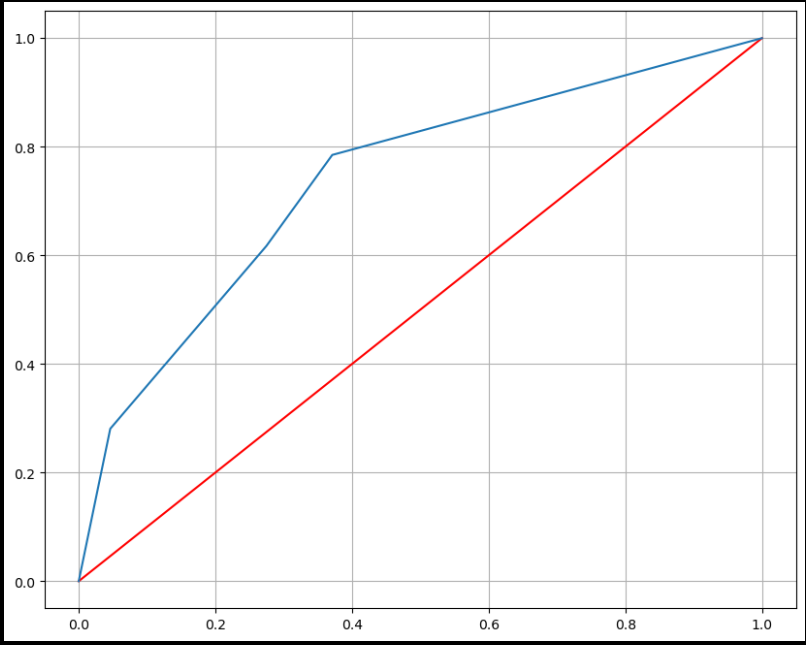 

Chapter 8 Pipeline

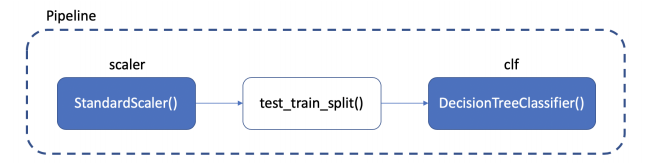
from sklearn.pipeline import Pipeline
from sklearn.tree import DecisionTreeClassifier
from sklearn.preprocessing import StandardScaler

estimators = [
    ('scaler', StandardScaler()),
    ('clf', DecisionTreeClassifier())
]

pipe = Pipeline(estimators)

• 새로운 명령을 만든 것
• 자주 사용하던 절차들을 하나의 명령어처럼 만들어서 쓸 수 있는 것

이 글은 제로베이스 데이터 취업 스쿨의 강의 자료 일부를 발췌하여 작성되었습니다