머신러닝 (6)

Chapter 9 Logistic Regression

• 이름은 regression이지만 실제로는 분류기
• 분류: 연속적이지 않은 값
• 회귀: 연속된 값
• 모든 회귀문제가 선형만 있는 것은 아니지만, 회귀 문제 중 가장 쉬운 것이 선형

비용함수 (cost function)

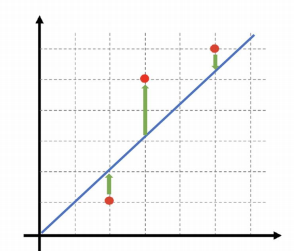
• 직선상에 있지 않은 세 점을 직선으로 표현하려면 에러가 발생할 수 밖에 없음

• 직선으로만 표현하려고 한다면 각 점과 직선 사이의 에러가 가장 작도록 함
  -> 각각의 에러를 구하고, 에러를 제곱(부호를 없애기 위해), 평균을 구함

• cost function을 최소화할 수 있으면 최적의 직선을 찾을 수 있음

• 비용함수의 최소값을 구하기 위해서
  -> 랜덤하게 임의의 점을 선택
  -> 임의의 점에서 미분(편미분) 값을 계산해서 업데이트
  -> 목표점의 오른쪽이면

  $\alpha \frac{d}{dt} J_{\theta}(x) > 0$
  $\theta := \theta - \{\text{Positive Value}\}$

  -> 목표점의 왼쪽이면

  $\alpha \frac{d}{dt} J_{\theta}(x) < 0$
  $\theta := \theta - \{\text{Negative Value}\}$

• Learning Rate

  $\theta := \theta - \alpha \frac{d}{dt} J_{\theta}(x)$

• 학습률이 작으면
  -> 최솟값을 찾으러 가는 간격이 작음
  -> 여러번 갱신해야 되지만 최소값에 잘 도달할 수 있음

• 학습률이 크다면
  -> 최솟값을 찾으러 가는 간격이 큼
  -> 최솟값을 찾으면 갱신횟수는 적겠지만, 수렴하지 않고 진동할 수도 있음

• Gradient Descent(경사하강법)

회귀를 분류에 적용

• 분류문제는 0 or 1로 예측해야 되지만 Linear Regression을 그대로 적용하면 예측값이 0보다 작거나 1보다 큰 값 가질 수 있음
• 예측값이 항상 0에서 1 사이 값을 가지도록 Hypothesis 함수를 수정

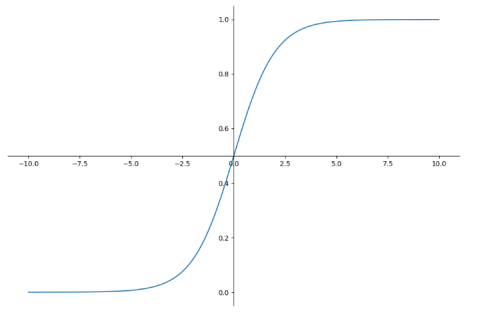
• Decision Boundary
  
  

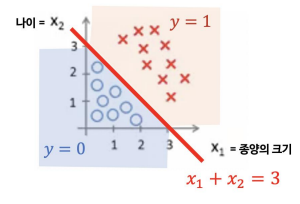
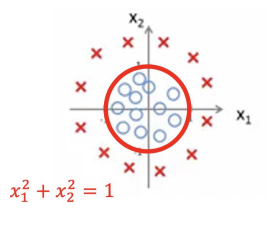
• Logistic Regression에서 Cost Function을 재정의

  $J(\theta) = \frac{1}{m} \sum_{i=1}^{m} \text{Cost}(h_\theta (x^{(i)}), y^{(i)})$
  $\text{Cost}(h_\theta (x), y) = \begin{cases} -\log(h_\theta (x)) & \text{if } y = 1 \\ -\log(1 - h_\theta (x)) & \text{if } y = 0 \end{cases}$

h = np.arange(0.01, 1 , 0.01)

c0 = -np.log(1 - h)
c1 = -np.log(h)

plt.figure(figsize=(12, 8))
plt.plot(h, c0 , label = 'y=0')
plt.plot(h, c1, label = 'y=1')
plt.legend()

plt.show()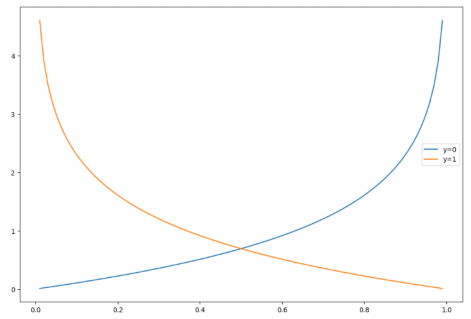

이 글은 제로베이스 데이터 취업 스쿨의 강의 자료 일부를 발췌하여 작성되었습니다