머신러닝v2 (4)

Chapter 4 분류 모델

분류 모델과 학습

• 분류 모델(Classification Model): 범주형 변수(categorical variable)를 구분하는 머신 러닝 모델
  -> 입력 받은 데이터가 어떤 범주에 속하는지 구분하는 모델
  -> 일반적으로 입력은 길이가 정해진 벡터를 사용한다.
  -> 출력은 각 범주를 숫자에 대응시켜 [0, 𝑀 − 1]의 양의 정수값을 사용
  

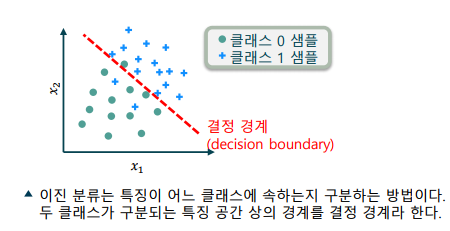
• 이진 분류 문제(Binary Classification Problem): 0과 1을 구분하는 가장 단순한 분류 문제
  -> 학습 데이터에는 각 특징에 대해 정답(label, groundtruth)이 주어짐
  -> 0과 1의 값은 숫자로서 의미가 없는 명목 변수
  -> 이 중 결정 경계를 정하는 일을 ‘모델을 학습한다’고 함
  

분류 모델의 과대적합과 과소적합

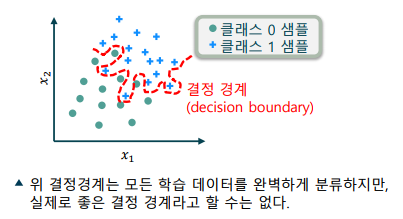
• 분류 모델의 과대적합(Overfitting): 학습 데이터에 편향(bias)되어, 모델의 성능이 하락하는 현상
  -> 학습 데이터만 보았을 때에는 매우 효과적으로 학습되는 것으로 보임
  -> 선택한 모델의 복잡도가 지나치게 높을 경우 발생
  -> 분산(variance)는 낮으나, 편향(bias)가 높은 상태라고 표현
  

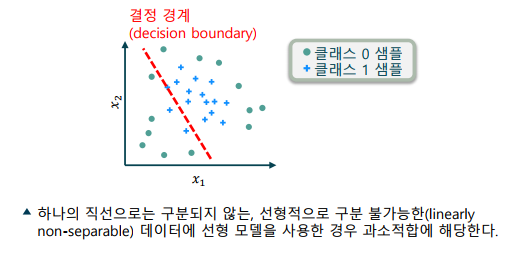
• 분류 모델의 과소적합(Underfitting): 모델의 표현력이 부족해, 성능이 하락하는 현상
  -> 모델이 학습 데이터를 충분히 구분하지 못함
  -> 편향(bias)는 낮으나, 분산(variance)가 크다고 표현
  

k-최근접이웃 분류 모델(KNN: k-Nearest Neighbors)

• 학습 데이터에서 가장 유사한 𝑘𝑘개의 특징을 찾아 타겟을 추정

• 게으른 학습기(lazy learner)로, 비모수 모델(nonparametric model)에 해당
  -> 게으른 학습기: 학습 데이터에서 미리 함수를 학습하지 않고, 새로운 입력이 주어지면 학습 데이터를 활용하는 학습기 (준비 시간은 짧지만, 실행 시간이 김)
  -> 비모수 모델: 모델의 학습 매개변수의 개수가 정해져 있지 않은 모델
  

• KNN 분류기(KNN Classifier)

• 동작
  -> KNN의 초매개변수 – 숫자 𝑘𝑘, 거리 측정 함수
  -> 학습 데이터 중에서 입력 특징과 가장 가까운 𝑘𝑘개 검출
  -> 최근접이웃 중 다수결로 투표하여 클래스를 추정

• 다양한 거리 측정 함수
  -> 유클리디안 거리, 맨해튼 거리, 민코스키 거리(Minkowski distance)
  -> 마할라노비스 거리(Mahalanobis distance) – 특징 간의 공분산(covariance)를 고려하여 측정하는 거리
  

로지스틱 회귀 모델

• 선형회귀(Linear Regression): 선형적인 관계에 있는 입,출력 관계를 분석하는 방법
  -> 단순 선형 회귀(simple linear regression): 1개의 특징(𝑥)으로 1개의 연속적인 타겟(𝑦)을 예측하는 모델
  -> 다변수 선형 회귀(multivariate linear regression): 여러 개의 특징(𝑥)으로 1개의 연속적인 타겟(𝑦)을 예측하는 모델
  

• 로지스틱 회귀(Logistic Regression): 선형 회귀를 이용해 분류 문제를 해결하는 방법
  -> 이진 분류(binary classification): 레이블이 0 또는 1의 범주(category)로 지정된 문제를 해결

• 로지스틱 함수(Logistic function)
  -> 출력 값의 범위를 [−∞,∞]에서 [0, 1] 사이로 제한하는 함수
  -> 로지스틱 함수의 출력은 0 ~ 100%의 ‘확률’을 표현할 수 있음
  

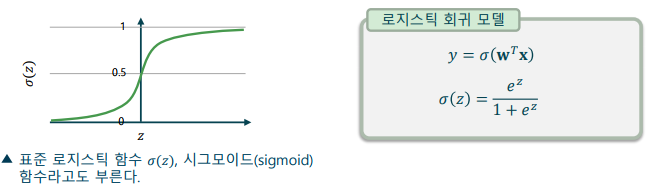
• 로지스틱 회귀 모델의 결정 경계
  -> 로지스틱 회귀 모델의 출력 값이 0.5보다 크면 클래스 1로 분류
  -> 선형 회귀에서 회귀 직선이, 로지스틱 회귀에서는 결정 경계가 됨

• 로지스틱 회귀 모델 출력의 의미
  -> 로지스틱 회귀의 출력(𝜎(𝑧))은 입력이 클래스 1일 확률
  -> 전체 확률의 합은 1이므로, 클래스 0일 확률은 (1−𝜎(𝑧))
  

로지스틱 회귀 모델의 학습

• 분류 문제의 손실 함수: 분류 문제에서 다루는 숫자는 연속형 변수가 아니므로, 선형 회귀와 달리 로지스틱 손실(logistic loss)를 사용
  -> 최대 가능도(maximum likelihood)로부터 유도된 손실 함수
  -> 0과 1 각 클래스 레이블에 대해 손실 함수가 대칭으로 발생
  

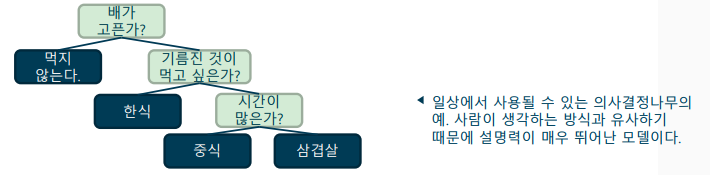
의사결정나무(Decision Tree)

• 단순한 기준으로 상황을 나누어 논리적인 판단을 도출하는 알고리즘: 정보 이론(imformation theory)를 기반으로 알고리즘 학습

• 의사결정나무의 장점
  -> 결과를 해석하고 이해하기 쉬움
  -> 정규화 등 특징을 가공할 필요가 없음
  -> 수치 자료형과 범주형 자료형을 모두 다룰 수 있음
  

• 트리구조(Tree Data Structure): 노드(node)와 간선(edge)로 이루어진 자료구조
  -> 연결된 두 노드 중 뿌리 노드에 가까운 노드를 부모 노드(parent node), 다른 노드를 자식 노드(child node)라고 함
  -> 뿌리 노드(root node): 트리 구조에서 최상단에 위치한 노드
  -> 잎새 노드(leaf node): 자식을 가지지 않는 노드
  -> 내부 노드(internal node): 잎새 노드가 아닌 노드
  

의사결정나무의 학습

• 학습 기준
  -> 정보 이득(information gain; IG)를 최대로 하는 기준 설정
  -> 잎새 노드의 불순도(impurity)를 최소화하는 것이 최종 목표

• 대표적인 불순도 지표(impurity indices): 지니 불순도(Gini impurity), 엔트로피 (entropy), 분류오차(classification error)
  

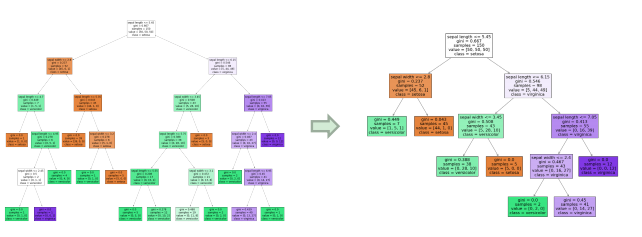
• 가지치기(Pruning): 의사결정나무의 학습이 완료된 후, 불필요한 노드를 제거
  -> 의사결정나무의 과대적합(overfitting)을 방지
  -> 사이킷런에서는 최소 비용-복잡도 가지치기(minimal cost-complexity pruning)으로 구현
  

서포트 벡터 머신(SVM: Support Vector Machine)

• 초평면을 이용하여 마진(margin)을 최대로 하는 분류 기법
  -로지스틱 회귀처럼 초평면으로 분리하나, 학습 방법이 다름
• 학습 데이터가 선형적으로 분리가능(linearly separable)할 때, 마진을 최대화 하는 알고리즘
  -> 마진(margin): 서포트 벡터 간의 거리
  -> 서포트 벡터(support vector): 결정 경계와 가장 가까운 학습 샘플
  

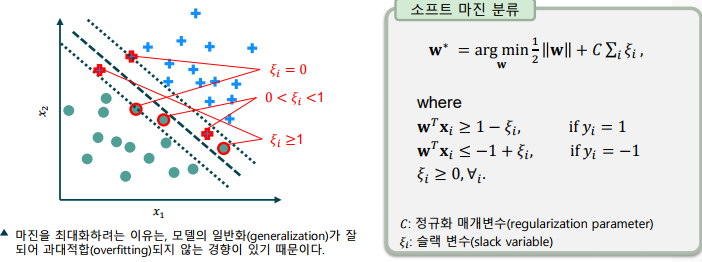
소프트 마진 분류 기법(Soft Margin Classification)

• 선형적으로 분리되지 않는 문제를 해결하기 위한 방법
  -> 슬랙 변수(slack variables)를 이용해 제약 조건을 완화
  -> 선형적으로 구분이 불가한 상황을 허용하되, 이것이 심할 수록 더 많은 페널티를 부여
  

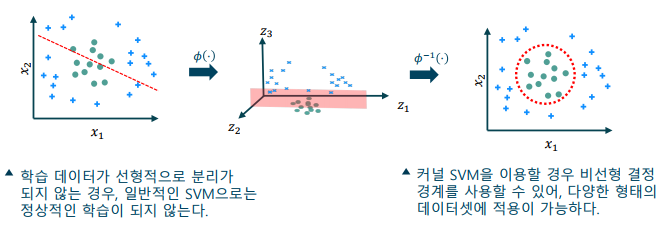
커널 소포트 벡터 머신(Kernel SVM, KSVM)

• 선형적으로 구분되지 않는 데이터셋에 적용
  -> 고차원 공간으로 매핑하여 분리 가능한 초평면 결정
  -> 원본 특징 공간에서 나타낼 경우 비선형 결정 경계(nonlinear decision boundary)가 됨
  

커널 트릭과 커널 함수

• 커널 트릭(Kernel Trick): 고차원 공간으로의 매핑을 수학적으로 유리하게 풀어내는 방법
  -> 고차원 공간 매핑을 명시적으로 할 경우, 연산량이 매우 증가
  -> SVM의 쌍대 형식(dual form)을 이용해 고차원 매핑된 특징간의 내적을 한번에 정의
  -> KKT(Karush-Kuhn-Tucker) condition에 의한 쌍대 형식 적용
  

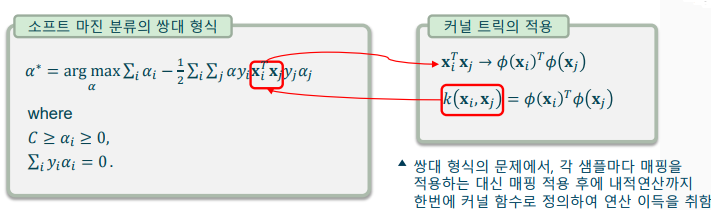
• 커널 함수의 종류
  

분류기의 평가 방법

• 손실 함수는 학습 과정에서 수학적으로 유리하지만, 성능 평가 지표로는 부적절
  -> 알고리즘에 따라 사용되는 손실 함수는 다를 수 있음
  -> 손실 함수가 낮은 것이 정확도(accuracy)를 보장하지는 않음
  -> 수학적 최적화 목표에는 적합하나, 비즈니스 목표와는 동떨어짐

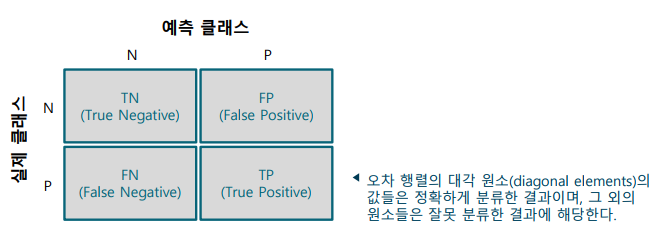
• 오차 행렬(Confusion Matrix)
  -> 혼동 행렬이라고도 불리며, 실제 클래스와 예측 클래스 결과를 행렬 형식으로 나열한 것
  -> 오차 행렬을 기반으로 하여 다양한 성능 지표를 계산할 수 있음
  

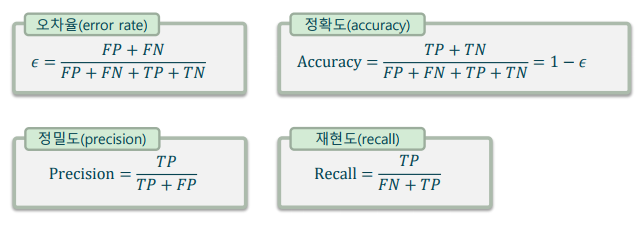
• 정밀도와 재현율(Precision and Recall): 오차율/정확도와 함께 분류 모델의 평가에 많이 사용되는 평가 지표
  -> 정밀도: ‘맞다’고 예측한 중에 맞춘 비율
  -> 재현도: 전체 실제 양성 클래스 중에 찾아낸 비율
  

• F1-Score: 정밀도와 재현도를 동시에 평가하기 위한 평가 지표
  -> 무조건 양성 클래스로 예측하면 재현도가 100%가 되며, 무조건 음성 클래스로 예측하면 정밀도가 100%가 되는 문제가 있음
  -> 정밀도와 재현도의 조화 평균으로 계산
  -> 두 값은 더할 수 없는 값이므로, 산술 평균이 아닌 조화 평균 사용
  

• ROC곡선 (Receiver Operating Characteristic Curve): 분류기의 단편적이 성능 뿐 아니라, 전반적인 성능을 평가
  -> ROC 곡선은 분류기의 문턱값(threshold value)를 바꾸어가며 평가
  -> FPR(false positive rate)와 TPR(true positive rate)를 기반으로 그래프에 곡선을 나타냄
  -> ROC AUC(area under curve)를 분류기 성능으로 사용
  

다중 분류기(Multi-class Classification)

• 세 종류 이상의 클래스를 구분하는 분류 기법
  -> 기본적으로 다중 분류를 지원하는 알고리즘: 의사결정나무, 소프트맥스 회귀(softmax regression)
  -> 이진 분류(binary classification)을 조합하여 다중 분류하는 방법
  -> One vs. Rest(OvR, One vs. All) – 각 클래스에 대해 긍정-부정으로 학습하는 방법 (𝑁개의 이진 분류기 학습)
  -> One vs. One(OvO) – 모든 클래스에 대해 상대적인 확률을 학습하는 방법 ($_𝑁𝐶_2$ =개의 이진 분류기 학습)
  

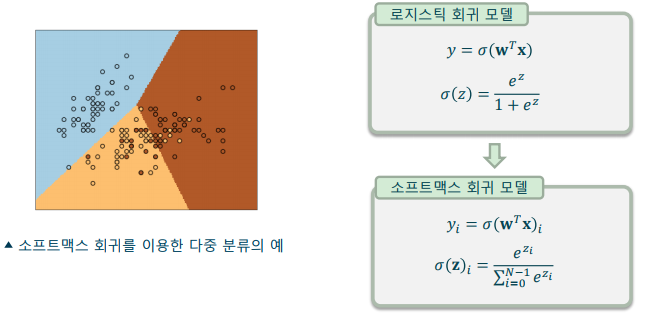
• 소프트맥스 회귀(Softmax Regression): 로지스틱 회귀를 다중 분류기로 확장하는 기법
  -> 딥러닝의 다중 분류에 주로 사용
  

이 글은 제로베이스 데이터 취업 스쿨의 강의 자료 일부를 발췌하여 작성되었습니다