
Chapter 5 회귀 모델
회귀 모델과 학습
-
회귀분석(Regression Analysis): 연속적인 출력 값을 예측하는 통계 분석 방법
-> 1886년 프랜시스 골턴의 연구에서, 세대가 흘러도 자녀의 키는 전체의 평균으로 ‘회귀’하는 것을 관찰한 것에서 유래 -
회귀 분석의 입력
-> 입력의 형식은 모델에 따라 다양한 형식이 될 수 있음
-> 특징(feature), 예측 변수(predictor variable), 설명 변수(explanatory variable) -
회귀 분석의 출력
-> 연속적인 출력 값(실수 값, 스칼라 값)
-> 타겟(target), 반응 변수(response variable), 결과(outcome) -
회귀 모델(Regression Model): 연속형 변수를 추정하는 머신 러닝 모델
-> 입력 받은 데이터가 어떤 출력 값을 가지는지 예측하는 모델
-> 일반적으로 입력은 길이가 정해진 벡터를 사용
-> 출력은 연속적인 값을 가지는 스칼라

-> 간격변수: 값의 간격에 의미가 있음
-> 비율변수: 값에 절대영점이 있음 -
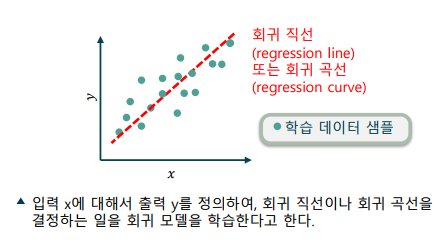
회귀 모델의 학습: 각 입력에 대해 출력을 매핑하여 모델을 학습
-> 학습 데이터에는 여러 개의 입력과 출력 쌍이 주어짐
-> 흔히 엑셀에서 말하는 “추세선”이 회귀 모델의 학습 결과
-> 모델에 따라 추세선은 직선이 되기도 하고, 곡선이 되기도 함
회귀 모델의 과대적합과 과소적합
-
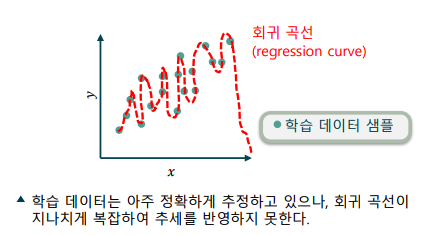
과대적합, Oveerfitting: 학습 데이터에 편향(bias)되어, 모델의 성능이 하락하는 현상
-> 학습 데이터만 보았을 때에는 매우 효과적으로 학습되는 것으로 보임
-> 선택한 모델의 복잡도가 지나치게 높을 경우 발생
-> 분산(variance)는 낮으나, 편향(bias)이 높은 상태라고 표현
-
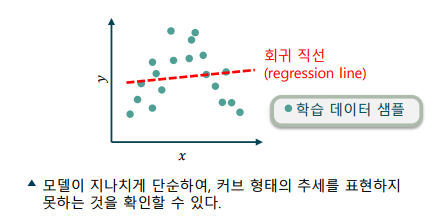
과소적합(Underfitting): 모델의 표현력이 부족해, 성능이 하락하는 현상
-> 모델이 학습 데이터를 충분히 따라가지 못함
-> 편향(bias)은 낮으나, 분산(variance)이 크다고 표현
단순 선형 회귀 이론
-
선형 회귀(Linear Regression): 선형적인 관계에 있는 입,출력 관계를 분석하는 방법
-
단순 선형 회귀(simple linear regression): 1개의 특징으로 1개의 연속적인 타겟을 예측 하는 모델

-
단순 선형 회귀의 학습: 최적의 직선을 찾는 매개변수 찾기
-> 매개변수 공간(parameter space): 학습 매개변수(가중치와 편향)를 모아 놓은 벡터 공간
-> 최소자승법(least squares method): 오차(error)의 제곱의 합이 최소가 되게 하는 학습 매개변수를 선택하는 최적화 방법

다중 선형 회귀 이론
-
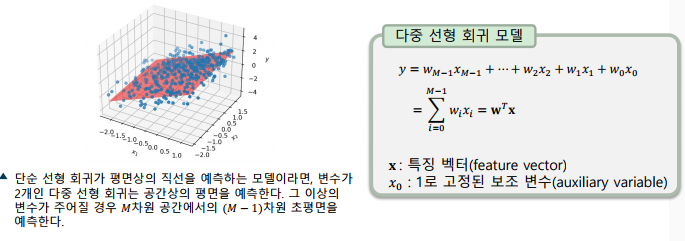
다중 선형 회귀(Multivariate Linear Regression)
-> 𝑀개의 특징()으로 연속적인 타겟(𝑦)을 예측하는 모델
-> 보조 변수(auxiliary variable)를 이용해 벡터의 내적으로 표현
-> 단순 선형 회귀와 동일한 최소자승법으로 학습
-
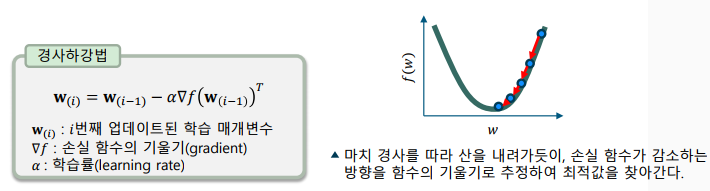
경사하강법(gradient descent method)
-> 여러 차례 값을 업데이트하여 최적해를 찾는 방법 중 하나
-> 손실 함수를 학습 매개변수로 미분하여 업데이트 방향과 크기 결정 -
손실함수(loss function)
-> 최적화 문제에서 최소화(또는 최대화) 하려는 목표가 되는 함수
-> 최적화 이론
규제 선형 회귀 모델
-
과대적합과 과소적합
-> 과대적합(overfitting): 모델이 지나치게 학습 샘플에 편향되어, 새로운 입력에 적절한 예측을 하지 못하는 문제
-> 과소적합(underfitting): 모델의 복잡도가 부족하여 학습 샘플의 입출력 관계를 충분히 설명하지 못하는 문제 -
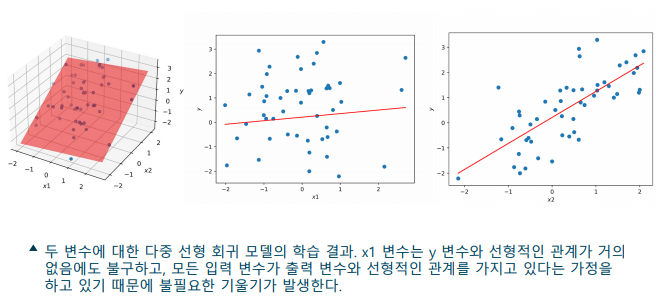
다중 선형 회귀 모델의 과대적합
-> 선형 회귀 모델은 기본적으로 모든 특징이 타겟과 선형 관계가 있다고 가정하기 때문에, 과대적합이 발생하는 경향이 있음
-> 과대적합의 해결 - 과도한 선형 관계에 대한 가정을 억제하면 과대적합을 방지하는 효과가 있음
-
규제(Regularization): 머신러닝 모델의 과대적합을 방지하는 방법 중 하나
-> 손실 함수에 복잡도에 대한 페널티를 부여하는 방법 -
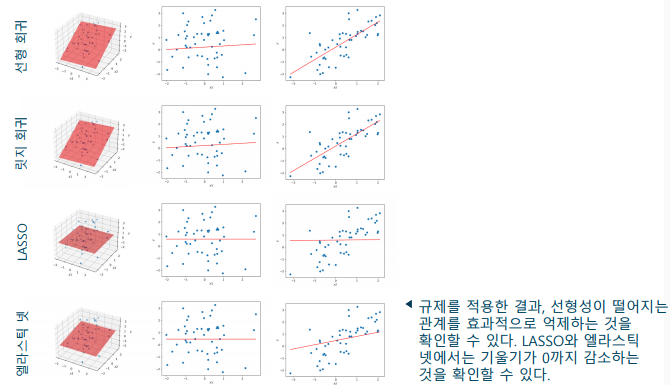
규제 선형 회귀 모델
-> 손실 함수는 오차의 제곱합을 그대로 사용
-> L2 규제: 릿지 회귀(ridge regression)
-> L1 규제: LASSO(least absolute shrinkage and selection operator)
-> L1 + L2 규제: 엘라스틱 넷(elastic net) -
릿지 회귀(Ridge Regression): 가중치의 L2 Norm을 규제함으로 사용
-> L2 Norm: 모든 가중치를 제곱하여 합한 결과
-> 편향()은 모델의 복잡도와 무관하므로, 규제 대상에서 제외 -
릿지 회귀의 특징: 규제 매개변수를 크게 해도 가중치의 값이 0이 되지는 않음

= LASSO: 가중치의 L1 Norm을 규제항으로 사용
-> L1 Norm: 모든 가중치의 절댓값을 합한 결과
-
LASSO의 특징
-> 규제 매개변수(𝜆)를 크게 하면 일부 가중치의 값이 0이 됨
-> 중요도가 낮은 특징을 제외하고자 할 때 사용(sparsity)
-> 𝑀>𝑁인 경우 최대 𝑁개의 특성만 사용

-
엘라스틱 넷(Elastic Net): 가중치의 L1, L2 Norm을 모두 규제항으로 사용
-> 릿지 회귀와 LASSO 사이의 절충 방식 -
엘라스틱 넷의 특징
-> LASSO와 같이 희소성을 가지지만, 𝑀>𝑁일 경우 L2 규제에 의해 보다 많은 특성을 선택
-> L1 규제와 L2 규제에 별도의 규제 매개변수를 사용

-
규제를 이용한 과대적합의 해결
k-최근접이웃 회귀 모델의 이론
-
학습 데이터에서 가장 유사한 k개의 특징을 찾아 타겟을 추정
-
게으른 학습기(lazy learner)로, 비모수 모델(nonparametric model)에 해당
-> 게으른 학습기: 학습 데이터에서 미리 함수를 학습하지 않고, 새로운 입력이 주어지면 학습 데이터를 활용하는 학습기
-> 비모수 모델: 모델의 학습 매개변수의 개수가 정해져 있지 않은 모델

-
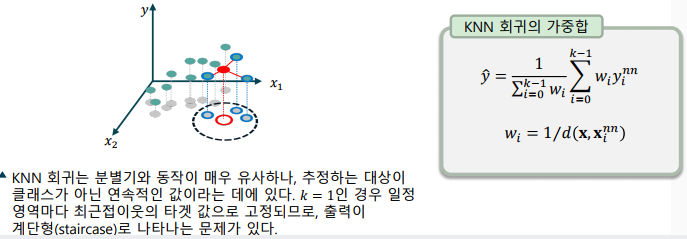
KNN 회귀 동작
-> KNN의 초매개변수: 숫자 𝑘, 거리 측정 함수
-> 학습 데이터 중에서 입력 특징과 가장 가까운 𝑘𝑘개 검출
-> 최근접이웃을 가중합(weighted sum)하여 타겟 추정
-> 입력과 이웃간 거리의 역수를 가중치로 사용(가까울 수록 큰 가중치)
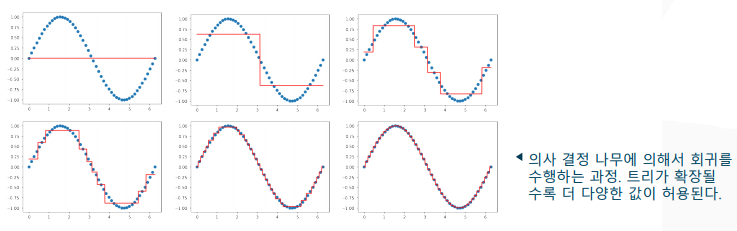
회귀 트리의 이론
- 회귀 트리(Regression Tree): 회귀 분석을 위한 의사 결정 나무
-> 불순도 대신 잎새 노드에서 잔차의 변동(분산)을 최소화
-> 잔차제곱(squared residual)이 유의미하게 향상되는지(p<0.05)를 기준으로 가지치기 수행
이 글은 제로베이스 데이터 취업 스쿨의 강의 자료 일부를 발췌하여 작성되었습니다