
Chapter 7 초매개변수 최적화
초매개변수(Hyperparameter)
-
학습 알고리즘에 의해 학습되지 않는 매개변수
-> 대표적인 초매개변수로 의사결정나무의 깊이, SVM의 소프트마진 매개변수 등이 있음
-> 그 외 모델을 생성할 때 결정해 주는 모든 매개변수를 초매개변수라고 할 수 있음
-> 초매개변수는 모델의 학습 결과에 지대한 영향을 끼침 -
초매개변수의 최적화
-> 초매개변수의 값을 고정한 후 모델을 학습
-> 학습된 모델의 성능을 검증하고 측정
-> 초매개변수의 값을 바꿔가면서 학습 결과가 더 좋아지게 하는 값을 찾음
모델의 검증 방법
- 모델의 학습 성능 뿐 아니라, 실사용 시나리오에서의 성능을 평가
-> 전체 데이터셋을 학습용과 검증용(validation)으로 나누어 사용
-> 평가 지표(evaluation metric) – 예측 상황에서 요구되는 모델의 성능으로, 비즈니스 목표와 연관이 깊음
-> cf) 손실 함수(loss function) – 모델의 성능 평가가 목적이 아닌, 모델의 학습 과정에서 수학적으로 유리한 함수
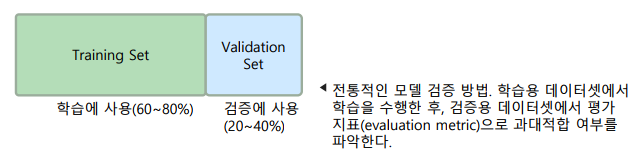
홀드아웃 교차 검증(Holdout Cross-Validation)
-
검증과 개선을 반복하면 검증 데이터셋에 과대적합되는 단점을 해결
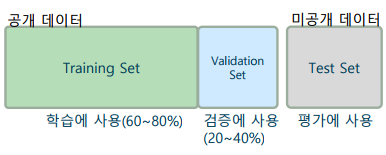
-> 데이터셋을 학습용, 검증용, 테스트용으로 나누어 사용
-> 테스트 데이터셋은 모델의 일반화 성능을 추정하는 데에만 사용 -
홀드아웃 교차 검증의 특징
-> 공정한 비교 평가를 위해 대회 등에서 주로 사용
-> 데이터셋을 나누는 방법에 따라 성능이 민감할 수 있음
k-폴드 교차 검증(k-Fold Cross Validation)
- 중복을 허용하지 않는 k개의 부분 데이터셋(폴드)으로 나누어 검증
-> k-1개의 폴드를 이용해 모델을 학습하고, 나머지 하나의 폴드로 검증
-> 총 k개의 모델을 학습/평가한 후, k개 모델의 평균 성능을 계산 - k-폴드 교차 검증의 특징
-> 여러 방법으로 모델을 학습/평가하므로 성능 평가가 안정적
-> 초매개변수의 최적화에 일반적으로 k-폴드 교차 검증을 사용

초매개변수 최적화 - 그리드 서치(Grid Search)
-
초매개변수 최적화를 위한 기본적인 방법
-> 초매개변수는 학습 알고리즘에 의해 결정되지 않으므로, 검증 기법 활용
-> 모델에 포함되는 초매개변수를 격자(grid) 형식으로 전수 조사
-> 조사할 초매개변수 범위에 대해 성능 평가하여 가장 좋은 모델 선택 -
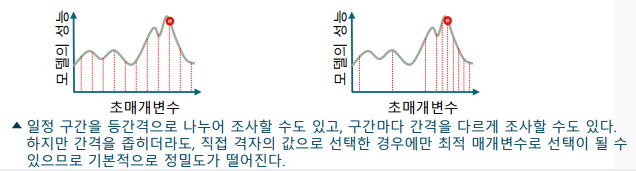
단점
-> 불필요한 공간도 모두 검사하므로, 연산량이 많음
-> 격자 위의 값만 검사하므로, 정밀도 떨어짐
초매개변수 최적화 - 랜덤 서치(Randomized Search)
- 초매개변수를 임의로 샘플링하여 탐색하는 기법
-> 초매개변수를 탐색할 범위를 정해두고, 임의로 샘플링하여 평가: 각 초매개변수의 분포를 이용하여 임의 샘플링의 성능 향상
-> 그리드 서치에 비해 더 적은 탐색 횟수로, 더 정밀한 결과를 도출: 충분히 큰 탐색 횟수를 가질 경우 통계적으로 성능이 보장됨

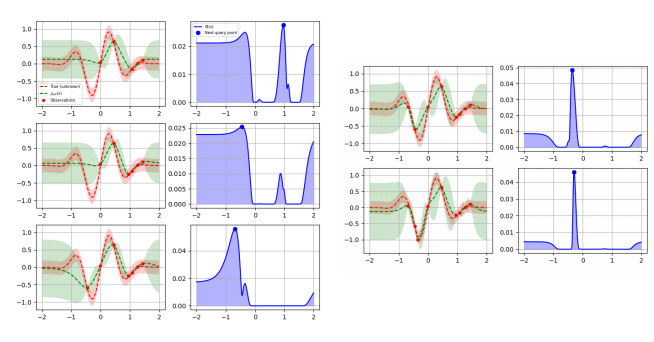
초매개변수 최적화 - 베이지언 서치(Bayesian Search)
- 머신러닝 모델 성능 향상을 위한 지능적인 초매개변수 탐색 방법
-> 1. 사전 확률 모델 정의: 가우시안 프로세스(Gaussian Process)와 같은 확률 모델로 초매개변수 공간의 사전 분포를 정의
-> 2. 목적 함수 평가: 초매개변수 조합에 대해 손실 함수 계산
-> 3. 사후 확률 업데이트: 평가된 초매개변수와 목적 함수 결과를 사용해 확률 모델을 업데이트
-> 4. 탐색-이용(Explore-Exploit) trade-off: 예상 개선치(expected improvement)등을 이용하여 새로운 초매개변수 후보 설정
-> 5. 반복 및 최적화: 단계 2-4를 반복하여 손실함수를 최소화 하는 초매개변수를 탐색
이 글은 제로베이스 데이터 취업 스쿨의 강의 자료 일부를 발췌하여 작성되었습니다