Chapter 9 차원 축소 기법
차원 축소 기법(Dimensionality Reduction)
- 특징 벡터의 정보를 유지하면서 차원을 감소시키는 기법
-> 머신 러닝 알고리즘에서 다룰 차원을 감소시켜 연산량 감소
-> 차원의 저주(curse of dimensionality) 문제를 개선
= 주로 비지도 학습법으로 차원 축소 수행
-> 데이터셋의 분포를 분석하여 더 적은 차원으로 데이터 압축
스칼라, 벡터, 행렬
- 벡터 변수(vector variable): 수학의 벡터를 나타내는 변수
-> 특별한 언급이 없으면 기본적으로 열 벡터(column vector)
-> 소문자 볼드체로 표현 (𝐱,𝐲,𝐳,…)
-> 또는, 소문자 볼드 이탤릭으로 표현 (𝒙,𝒚,𝒛,…)
= 행렬 변수(matrix variable): 수학의 행렬을 나타내는 변수
-> 대문자 이탤릭으로 표현 (𝑋,𝑌,𝑍,…)

고윳값 분해(Eigen Decomposition)
- 정방 행렬을 고윳값과 고유벡터들로 나누는 분해 방법
-> 행렬의 고윳값과 고유벡터를 구한 후, 대각화(diagonalization)하여 행렬을 분해 - 고유벡터와 고윳값의 의미
-> 중복과 복소수 해를 포함하여 총 𝑁개(행렬의 행/열의 길이) 존재
-> 고유벡터: 행렬 𝐴를 곱하더라도 방향이 바뀌지 않는 길이가 1인 벡터
-> 고윳값: 행렬 𝐴를 곱하기 전과 후의 크기 비율

특잇값 분해(SVD: Singular Value Decomposition)
- 정방 행렬이 아닌 𝑁×𝑀크기의 행렬 𝐴𝐴를 분해하는 고윳값 분해와 유사한 행렬 분해 방법
-> 특잇값 분해는 모든 행렬에 대해서 가능하다.
-> 모든 특이벡터는 크기가 1이고(unit vector), 특이벡터들은 서로 직교함(orthogonal)

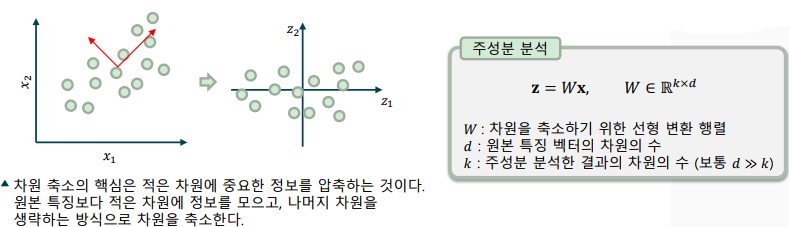
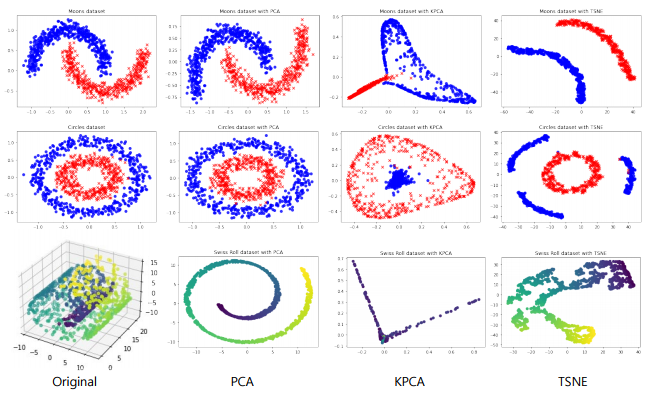
주성분 분석(PCA: Principal Component Analysis)
-
원본 차원에서 분산이 큰 방향으로 축을 변환하는 비지도 학습 기법
-> 특징 추출(feature extraction), 잡음 제거(noise reduction) 등의 역할로 많이 사용
-> 분산이 가장 큰 축을 기준으로 분산이 큰 순으로 직교 좌표계 구성
-> 원본 차원과 동일 차원 수 까지 표현 가능, 일부 차원을 생략할 수 있음
-
PCA 학습 알고리즘
-> 1. 특징 벡터를 표준화하여 전처리(standardization)
-> 2. 학습 데이터셋에서 공분산 행렬(covariance matrix) 계산
-> 3. 공분산 행렬을 고윳값와 고유벡터로 분리
-> 4. 고윳값이 큰 순서대로 정렬후, 𝑘개의 고유 벡터를 모아 행렬 𝑊 구성

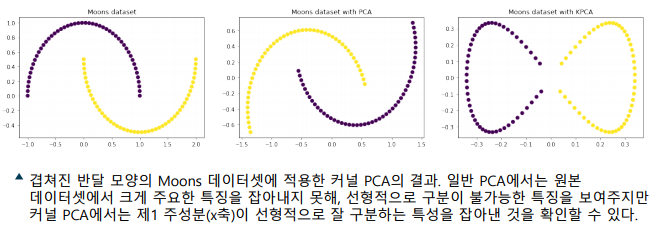
커널 주성분 분석(Kernel PCA)
- 주성분 분석에 비선형 매핑을 적용하는 기법
-> 명시적으로 비선형 매핑할 경우, 연산량이 급격히 증가
-> 원본 특징 공간에서 계산하기 위해 커널 트릭(kernel trick) 사용
--> PCA 계산 과정에서 특징 간의 공분산에 비선형 매핑 적용
--> SVM에서 유도한 커널 트릭과 같이 유사도 함수로 커널 선택

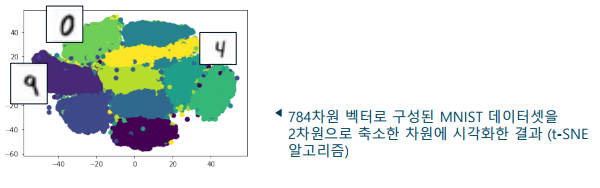
t-SNE(Stochastic Neighbor Embedding)
- 고차원의 특징 벡터의 시각화를 위해 저차원 공간에 투영하는 기법
-> 샘플의 이웃을 유지함녀서 투영하여 시각화에 유리 - 확률적(stochastic) - 문제를 확률에 대한 문제로 정의하여 해결
-> 원 공간과 저차원에서 샘플 간에 이웃일 확률 분포가 유사하게 최적화
-> KL 발산(Kullback-Leibler divergence): 확률 분포가 얼마나 차이나는지 [0, 1]의 값으로 나타내는 함수

이 글은 제로베이스 데이터 취업 스쿨의 강의 자료 일부를 발췌하여 작성되었습니다