트리(Tree)
- 부모와 자식 관계로 이어진 노드의 집합으로 이루어진 자료구조
- 계층적 구조를 나타낼 때 주로 사용
-> 폴더 구조, 조직도, 가계도 ..
트리의 구조
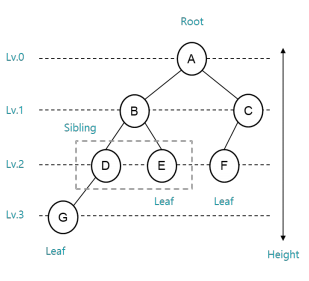
- 노드(Node): 트리 구조의 자료 값을 담고 있는 단위
- 에지(Edge): 노드 간의 연결선 (=link, branch)
- 루트 노드(Root): 부모가 없는 노드, 가장 위의 노드
- 잎새 노드(Leaf): 자식이 없는 노드 (=단말)
- 내부 노드(Internal): 잎새 노드를 제외한 모든 노드
- 부모(Parent): 연결된 두 노드 중 상위의 노드
- 자식(Child): 연결된 두 노드 중 하위의 노드
- 형제(Sibling): 같은 부모를 가지는 노드
= 깊이(Depth): 루트에서 어떤 노드까지의 간선의 수 - 레벨(Level): 트리의 특정 깊이를 가지는 노드 집합
- 높이(Height): 트리에서 가장 큰 레벨 값
- 크기(Size): 자신을 포함한 자식 노드의 개수
- 차수(Degree): 각 노드가 지닌 가지의 수
- 트리의 차수: 트리의 최대 차수
트리의 특징
- 하나의 노드에서 다른 노드로 이동하는 경로는 유일
- 노드가 𝑁개인 트리의 간선의 수는 𝑁 − 1개
- Acyclic (Cycle이 존재하지 않음)
- 모든 노드는 서로 연결되어 있음
- 하나의 간선을 끊으면 2개의 부분 트리(sub-tree)로 분리됨
이진 트리(Binary tree)
- 각 노드는 최대 2개의 자식을 가질 수 있음
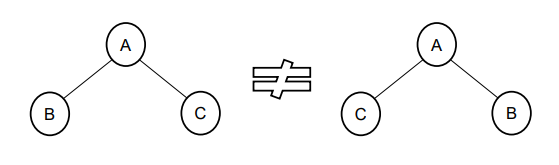
- 자식 노드는 좌우를 구분함
-> 왼쪽 자식: 부모 노드의 왼쪽 아래
-> 오른쪽 자식: 부모 노드의 오른쪽 아래
이진 트리의 종류
-
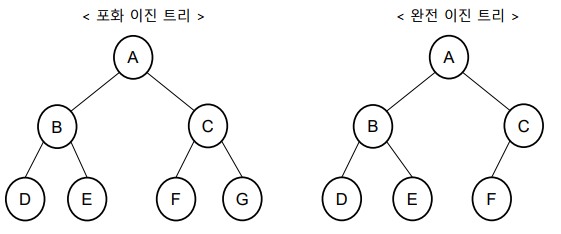
포화 이진 트리(Perfect binary tree): 모든 레벨에서 노드들이 꽉 채워져 있는 트리
-
완전 이진 트리(Complete binary tree): 마지막 레벨을 제외하고 노드들이 모두 채워져 있는 트리
-
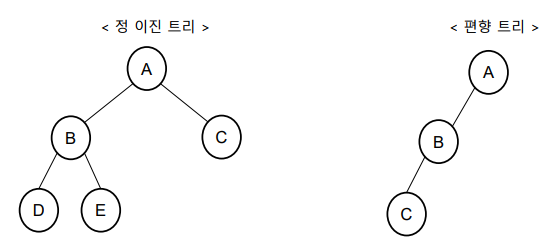
정 이진 트리(Full binary tree): 모든 노드가 0개 또는 2개의 자식 노드를 갖는 트리
-
편향 트리(Skewed binary tree): 한쪽으로 기울어진 트리
-
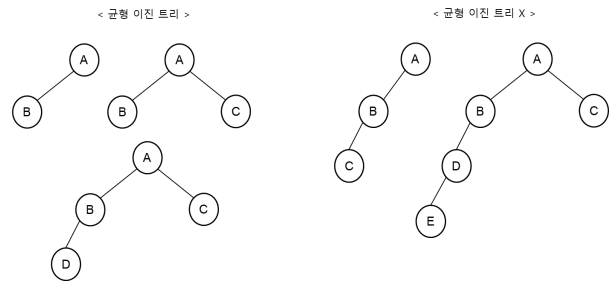
균형 이진 트리(Balanced binary tree): 모든 노드의 좌우 서브 트리 높이가 1이상 차이 나지 않는 트리
이진 트리의 특징
- 포화 이진 트리의 높이가 h일때, 노드의 수는 개
- 포화(or 완전) 이진 트리의 노드가 N개 일 때, 높이는
- 이진 트리의 노드가 N개 일때, 최대 가능 높이는 N
이진 트리의 순회(Traversal)
- 모든 노드를 빠뜨리거나 중복하지 않고 방문하는 연산
- 비선형 자료구조이기 때문에 다양한 순회 방법이 있음
- 전위 순회, 대칭 순회, 후위 순회: 재귀적 순회 방법
- 레벨 순회: 레벨 별 순회 방법
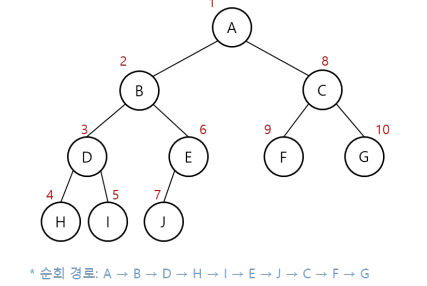
전위 순회(Preorder traversal)
- 깊이 우선 순회(Depth first traversal)이라고도 함
- 방문 순서: 현재 노드 → 왼쪽 노드 → 오른쪽 노드
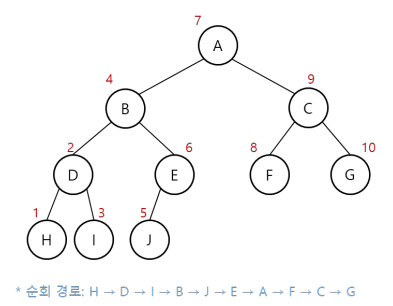
대칭 순회(Inorder traversal)
- 방문 순서: 왼쪽 노드 → 현재 노드 → 오른쪽 노드
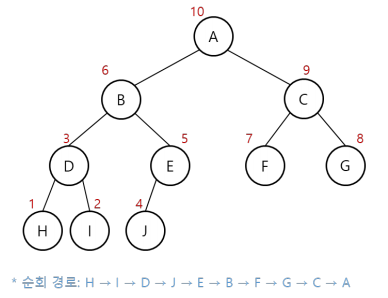
후위 순회(Postorder traversal)
- 방문 순서: 왼쪽 노드 → 오른쪽 노드 → 현재 노드
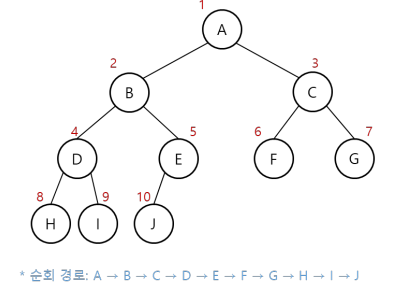
레벨 순회(Level order traversal)
- 너비 우선 순회 (Breadth first traversal)이라고도 함
- 방문 순서: 위쪽 레벨 부터 왼쪽 노드 → 오른쪽 노드
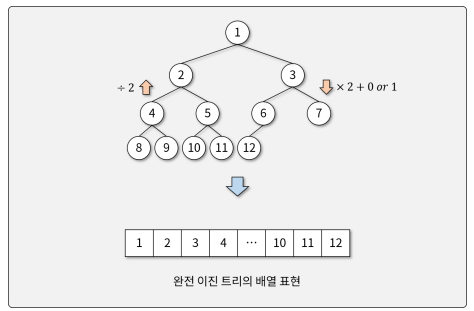
완전 이진 트리의 구현
- 배열에 레벨 순회 순서대로 배열로 구성
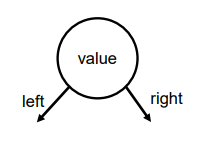
일반적인 이진 트리의 구현
-
Node 클래스를 이용하여 구현: value, left, right 멤버 변수를 가지는 클래스
-
Root node를 멤버 변수로 가지는 클래스 Tree 구현
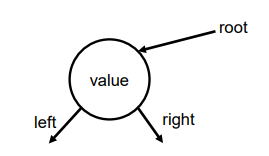
트리의 구현
1) 배열(리스트)를 기반으로 하는 완전이진트리를 구현하시오
class BinaryTree:
def __init__(self, data):
self.data = [-1] + data # 첫번째 노드가 인덱스 1로 시작
def preorder(self):
def recursive(node):
if node >= len(self.data):
return
# 현재 노드를 방문
print(self.data[node], end=' ')
# 좌측 자식 방문
recursive(2*node)
# 우측 자식 방문
recursive(2*node + 1)
recursive(1)
print()
def inorder(self):
def recursive(node):
if node >= len(self.data):
return
# 좌측 자식 방문
recursive(2*node)
# 현재 노드를 방문
print(self.data[node], end=' ')
# 우측 자식 방문
recursive(2*node + 1)
recursive(1)
print()
def postorder(self):
def recursive(node):
if node >= len(self.data):
return
# 좌측 자식 방문
recursive(2*node)
# 우측 자식 방문
recursive(2*node + 1)
# 현재 노드를 방문
print(self.data[node], end=' ')
recursive(1)
print()
def levelorder(self):
# 배열로 표현된 완전이진트리는 이미 레벨오더 순회 순서로 되어 있다.
for value in self.data[1:]:
print(value, end=' ')
print()
def bfs(self, value):
for elem in self.data[1:]:
if value == elem:
return True
return False
def dfs(self, value):
is_found = False
def recursive(node):
nonlocal is_found
if node >= len(self.data):
return
# value를 이미 찾았다면, 추가 탐색 불필요
if is_found:
return
# 현재 노드를 방문
if self.data[node] == value:
is_found = True
return
# 좌측 자식 방문
recursive(2*node)
# 우측 자식 방문
recursive(2*node + 1)
recursive(1)
return is_found
tree = BinaryTree([i for i in range(13)])
tree.preorder()
tree.inorder()
tree.postorder()
tree.levelorder()
print(tree.dfs(15))
print(tree.dfs(11))
print(tree.bfs(6))
print(tree.bfs(17))2) Node를 이용하여 완전 이진 트리를 구현하시오
class Node:
def __init__(self, value, left=None, right=None):
self.value = value
self.left = left
self.right = right
class BinaryTree:
def __init__(self, array):
node_list = [Node(value) for value in array]
for ind, node in enumerate(node_list):
left = 2 * ind + 1
right = 2 * ind + 2
if left < len(node_list):
node.left = node_list[left]
if right < len(node_list):
node.right = node_list[right]
self.root = node_list[0]
def preorder(self):
def recursive(node):
if node is None:
return
# 현재 노드 방문
print(node.value, end=' ')
# 왼쪽 자식 노드
recursive(node.left)
# 오른쪽 자식 노드
recursive(node.right)
recursive(self.root)
print()
def inorder(self):
def recursive(node):
if node is None:
return
# 왼쪽 자식 노드
recursive(node.left)
# 현재 노드 방문
print(node.value, end=' ')
# 오른쪽 자식 노드
recursive(node.right)
recursive(self.root)
print()
def postorder(self):
def recursive(node):
if node is None:
return
# 왼쪽 자식 노드
recursive(node.left)
# 오른쪽 자식 노드
recursive(node.right)
# 현재 노드 방문
print(node.value, end=' ')
recursive(self.root)
print()
def levelorder(self):
if self.root is None:
return
queue = []
queue.append(self.root)
while queue:
node = queue.pop(0)
# 큐에서 뽑은 노드를 방문
print(node.value, end=' ')
if node.left:
queue.append(node.left)
if node.right:
queue.append(node.right)
print()
def bfs(self, value):
if self.root is None:
return
queue = []
queue.append(self.root)
while queue:
node = queue.pop(0)
# 큐에서 뽑은 노드를 방문
if node.value == value:
return True
if node.left:
queue.append(node.left)
if node.right:
queue.append(node.right)
return False
def dfs(self, value):
is_found = False
def recursive(node):
nonlocal is_found
if node is None:
return
if is_found:
return
# 현재 노드 방문
if value == node.value:
is_found = True
return
# 왼쪽 자식 노드
recursive(node.left)
# 오른쪽 자식 노드
recursive(node.right)
recursive(self.root)
return is_found
tree = BinaryTree([i for i in range(13)])
tree.preorder()
tree.inorder()
tree.postorder()
tree.levelorder()
print(tree.dfs(15))
print(tree.dfs(11))
print(tree.bfs(6))
print(tree.bfs(17))힙(Heap)
- 완전 이진 트리의 일종으로, 우선순위 큐(Priority queue)라고도 함
- 최소값 또는 최댓값을 빠르게 찾아내는데 유용한 자료구조
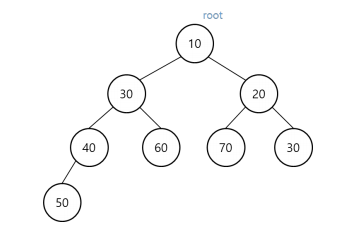
최소 힙(Min heap)
- 부모 노드의 value ≤ 자식 노드의 value 상태로 항상 정렬되어 있는 자료구조
- 동일한 자료에 대해서 여러가지 최소 힙이 성립
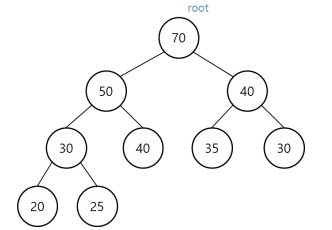
최대 힙(Max heap)
- 부모 노드의 value ≥ 자식 노드의 value 상태로 항상 정렬되어 있는 자료구조
- 동일한 자료에 대해서 여러가지 최대 힙이 성립
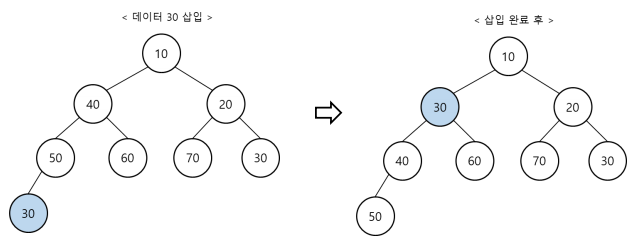
최소힙-삽입
- 트리의 가장 끝 위치에 데이터 삽입
- 부모 노드와 키 비교한 후 작을 경우 부모 자리와 교체 (반복)
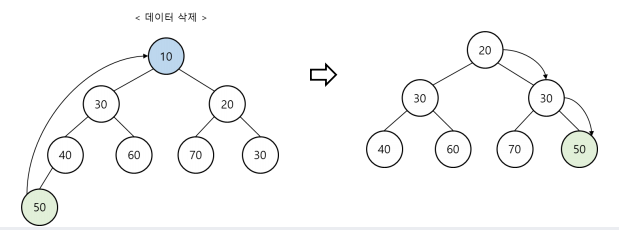
최소힙-삭제
- 최상위 노드 반환 및 삭제
- 가장 마지막 위치의 노드를 최상위 노드로 위치 시킴
- 자식 노드 중 작은 값과 비교 후 부모 노드가 더 크면 자리 교체 (반복)
힙의 장점
- 일반 배열에서 최대값/최소값을 찾아 반환하는 연산: O(N)
- 일반 배열에 새로운 자료를 추가하는 연산: O(1)
- 정렬된 배열에서 최대값/최소값을 찾아 반환하는 연산: O(1) (단, 정렬하는 연산 O(NlogN)이 선행되어야 함)
- 정렬된 배열에 새로운 자료를 추가하는 연산: O(N)
- Heap에서 최대값/최소값을 찾아 반환하는 연산: O(logN)
- Heap에 새로운 자료를 추가하는 연산: O(logN)
힙의 활용
from heapq import heappop, heappush, heapify
# heapq 패키지를 이용한 min heap 사용법
heap = []
for elem in [4, 10, 8, 0, 10, 9, 2]:
heappush(heap, elem)
print(heap)
while heap:
data = heappop(heap)
print(data, end=' ')
print()
# heapq 패키지를 이용한 max heap 사용법
heap = []
for elem in [4, 10, 8, 0, 10, 9, 2]:
heappush(heap, -elem)
print(heap)
while heap:
data = -heappop(heap)
print(data, end=' ')
print()
# heapq 패키지를 이용한 priority queue 사용법
pq = []
# (우선순위(작을수록 높음), 값)
for elem in [(1, 10), (4, 14), (-2, 5), (10, 6)]:
heappush(pq, elem)
while pq:
data = heappop(pq)
print(data[1], end=' ')
print()
# heapify를 사용하는 방법: 일반적인 배열(리스트)를 힙으로 변경
heap = [4, 10, 8, 0, 10, 9, 2]
heapify(heap)
while heap:
data = heappop(heap)
print(data, end=' ')
print()1) 슬라이딩 최댓값, 리스트 arr에 정수로 이루어진 자료가 주어져 있다.이 때, 연속된 k개 중 최댓값을 구하고 싶다.
예를 들어, arr = [1, 3, 5, 2, 7, 4]이고 k = 3이라면
첫번째 최댓값은 max([1, 3, 5]) -> 5
두번째 최댓값은 max([3, 5, 2]) -> 5
세번째 최댓값은 max([5, 2, 7]) -> 7
네번째 최댓값은 max([2, 7, 4]) -> 7
따라서 결과는 [5, 5, 7, 7]이 된다.
이 프로그램을 구현하시오.
from heapq import heapify, heappush
def solution(arr, k):
result = []
window = list(map(lambda x: -x, arr[:k]))
heapify(window) # 이거 필수!!!
result.append(-window[0])
for i in range(len(arr) - k):
window.remove(-arr[i])
heapify(window) # 이거 필수!!!
heappush(window, -arr[i+k])
result.append(-window[0])
return result
if __name__ == '__main__':
arr = [1, 3, 5, 2, 7, 4]
k = 3
sol = solution(arr, k)
print(sol)2) 누적 중간값, 리스트 arr에 정수로 이루어진 자료가 주어져 있다. 출력 역시 정수로 이루어진 동일한 길이의 리스트로, 이 리스트의 i번째 값은 arr의 처음부터 i번째까지 값의 중간값이다. 단, 짝수개의 값의 중간값은 중간값 2개의 평균으로 계산한다. 이 프로그램을 구현하시오.
from heapq import heappush, heappop
def solution(arr):
min_heap = []
max_heap = []
result = []
for elem in arr:
if not min_heap or elem >= min_heap[0]:
heappush(min_heap, elem)
if len(min_heap) > len(max_heap) + 1:
heappush(max_heap, -heappop(min_heap))
else:
heappush(max_heap, -elem)
if len(max_heap) > len(min_heap):
heappush(min_heap, -heappop(max_heap))
if len(max_heap) == len(min_heap):
# 자료가 짝수개일 때 중앙값 2개 평균
result.append((-max_heap[0] + min_heap[0]) / 2.0)
else:
# 자료가 홀수개일 떄 중앙값
result.append(min_heap[0])
return result
if __name__ == '__main__':
arr = [1, 3, 5, 2, 7, 4, 5, 23, -4, 52, 45]
sol = solution(arr)
print(sol)이 글은 제로베이스 데이터 취업 스쿨의 강의 자료 일부를 발췌하여 작성되었습니다