
그래프(Graph)
- 객체 간에 짝을 이루는 가장 유연한 자료 구조
- 정점(vertex, node, point)와 이를 잇는 간선(edge)로 구성
- 간선은 무향(undirected) 또는 유향(directed)일 수 있음
- 간선에는 가중치(weight)가 있을 수 있으며, 이는 연결의 강도나 간선의 길이를 의미
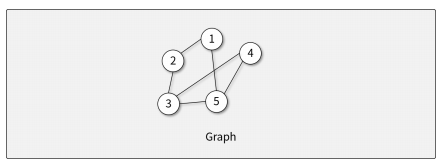
그래프의 구조
- 정점(Vertex): 각 노드
- 간선(Edge): 노드와 노드를 연결하는 선 (link, branch)
- 인접 정점(Adjacent vertex): 간선 하나를 두고 바로 연결된
- 정점 정점의 차수(Degree):
-> 무방향 그래프에서 하나의 정점에 인접한 정점의 수
-> 무방향 그래프 모든 정점 차수의 합 = 그래프 간선의 수 2배 - 진입 차수(In-degree): 방향 그래프에서 외부에서 오는 간선의 수
- 진출 차수(Out-degree): 방향 그래프에서 외부로 나가는 간선의 수
- 경로 길이(Path length): 경로를 구성하는데 사용된 간선의 수
- 단순 경로(Simple path): 경로 중에서 반복되는 정점이 없는 경우
- 사이클(Cycle): 단순 경로의 시작 정점과 끝 정점이 동일한 경우
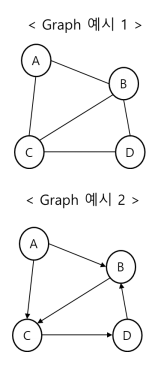
그래프의 구현
-
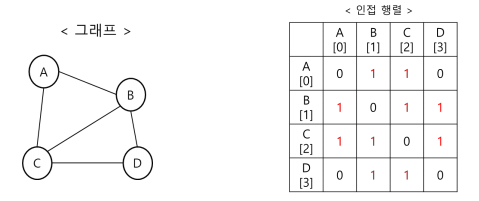
인접행렬(Adjacency matrix): 이차원 배열 이용
-
인접 행렬의 장단점
-> 간선 정보의 확인과 업데이트가 빠름
-> 인접 행렬을 위한 메모리 공간 차지
-
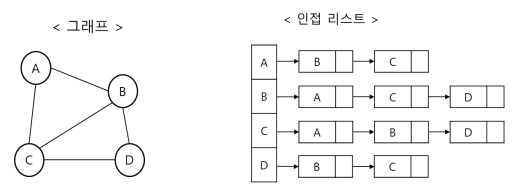
인접 리스트(Adjacency list): 연결리스트 이용
-
인접 리스트의 장단점
-> 메모리 사용량이 상대적으로 적고, 노드의 추가 삭제 빠름
-> 간선 정보 확인이 상대적으로 오래 걸림
그래프의 종류
-
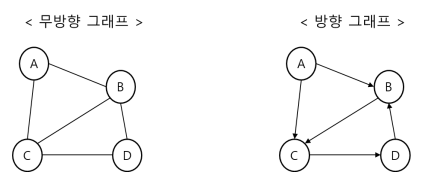
무방향 그래프(Undirected graph)
-> 간선에 방향이 없는 그래프 (양방향 이동 가능)
-> 정점 A - B 간선의 표현: (A, B) = (B, A) -
방향 그래프 (Directed graph)
-> 간선에 방향이 있는 그래프 (해당 방향으로만 이동 가능)
-> 정점 A → B 간선의 표현: <A, B> ≠ <B, A>
-
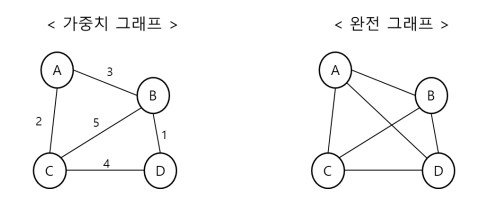
가중치 그래프 (Weighted graph)
-> 간선에 가중치가 있는 그래프 (이동 비용 or 연결 강도) -
완전 그래프 (Complete graph)
-> 모든 정점이 서로 연결되어 있는 그래프
-> 정점이 𝑁개일 경우, 간선의 수는 𝑁(𝑁 − 1)/2 개
그래프의 탐색
-
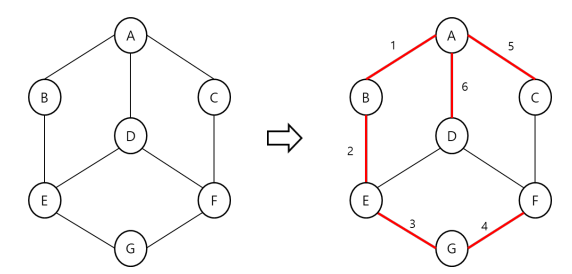
깊이 우선 탐색(DFS: Depth first search): visited 배열과 스택 또는 재귀적으로 구현(Preorder)
-
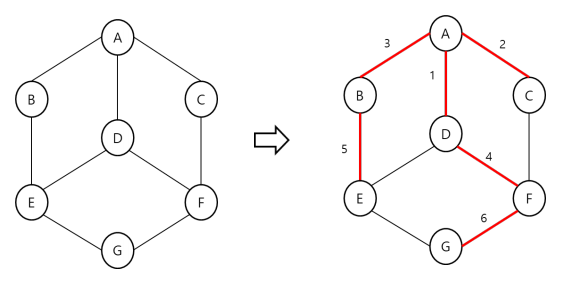
너비 우선 탐색(BFS: Breath first search): 각 노드에 방문했는지 여부를 체크할 배열과 큐 이용하여 구현
그래프의 구현
- 인접 리스트로 그래프의 bfs와 dfs 구현
class Vertex:
def __init__(self, value, adj_list=None):
self.value = value
self.adj_list = adj_list if adj_list else []
class Graph:
def __init__(self):
self.vertices = []
def insert(self, value, adj_list):
self.vertices.append(Vertex(value, adj_list))
for adj_ind in adj_list:
self.vertices[adj_ind].adj_list.append(len(self.vertices) - 1)
def bfs(self, vert_ind, value):
visited = [False for _ in range(len(self.vertices))]
queue = []
queue.append(vert_ind)
while queue:
node_ind = queue.pop(0)
if visited[node_ind]:
continue
visited[node_ind] = True
node = self.vertices[node_ind]
if node.value == value:
return True
for adj_ind in node.adj_list:
queue.append(adj_ind)
return False
def dfs(self, vert_ind, value):
is_found = False
visited = [False for _ in range(len(self.vertices))]
def recursive(node_ind):
nonlocal is_found
# 이미 value를 찾았으면 바로 종료
if is_found:
return
# 이미 visit한 노드라면 종료
if visited[node_ind]:
return
# 처음 방문하는 노드라면 visit을 True로 변경
visited[node_ind] = True
node = self.vertices[node_ind]
# 현재 노드의 값이 찾고자 하는 value인지 검사
if node.value == value:
is_found = True
return
# 인접한 모든 노드를 재귀적으로 호출
for adj_index in node.adj_list:
recursive(adj_index)
recursive(vert_ind)
return is_found
graph = Graph()
graph.insert(0, [])
graph.insert(1, [0])
graph.insert(2, [1])
graph.insert(3, [2])
graph.insert(4, [0, 2, 3])
print(graph.bfs(0, 2))
print(graph.dfs(0, 3))트라이(Trie)
- 검색 트리(Retrieval tree)
- 문자열을 저장하고 빠르게 탐색하기 위한 자료 구조
- 트라이를 구성하기 위한 별도의 메모리가 필요하나, 매우 빠른 탐색이 가능
-> 단순 문자열 탐색: 𝑂(𝑀N), 트라이에서 탐색: 𝑂(𝑀) (𝑀: 문자열의 길이, N: 문자열의 개수)
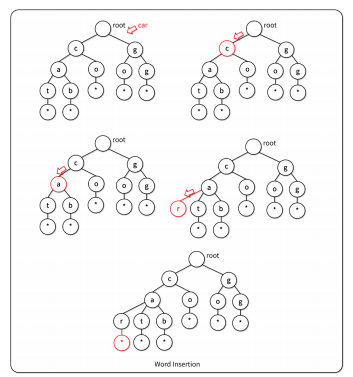
자료의 입력
- 각 노드는 문자열의 각 문자를 의미
- 루트 노드에서 시작하여, 문자열의 문자를 순서대로 자식 노드로 생성
- 기존에 같은 문자를 가진 자식 노드가 있다면, 새 노드를 생성하지 않고 해당 노드를 사용
- 모든 문자열 입력이 끝나면, 마지막에 END문자(*)를 입력
자료의 탐색
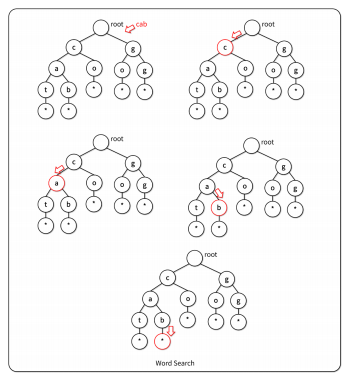
- 루트 노드부터 시작하여, 문자열의 각 문자를 하나씩 자식 노드에서 찾아감
- 자식 노드 중에 문자가 없으면 해당 문자열은 트라이에 존재하지 않음
- 모든 문자를 탐색한 후에, END문자(*)까지 찾으면 해당 문자열은 트라이에 존재
트라이의 활용
1) Trie 자료구조 구현
class Node:
def __init__(self):
self.children = dict()
class Trie:
def __init__(self):
self.root = Node()
def add_word(self, word):
curr = self.root
for c in word:
if c not in curr.children:
curr.children[c] = Node()
curr = curr.children[c]
curr.children['*'] = Node()
def search(self, query):
curr = self.root
for c in query:
if c not in curr.children:
return False
curr = curr.children[c]
return '*' in curr.children
trie = Trie()
words = ['abc', 'abcd', 'bcd', 'zzz', 'zz', 'zerobase', 'zero']
for word in words:
trie.add_word(word)
queries = ['abc', 'ab', 'zz', 'zzzz', 'zero', 'zerob']
# True False True False True False
result = []
for query in queries:
result.append(trie.search(query))
print(result)2) 와일드 카드 검색기, 검색할 단어가 리스트 words에 주어져 있다. 이 words에 queries에 있는 단어로 시작하는 단어를 모두 찾으려 한다. 예를 들어, words = ["buy", "bull", "bucket", "bill"] 일 때, "bu"를 검색하면 "bu"로 시작하는 단어 "buy", "bull", "bucket"이 일치하여 답은 3이 된다. 이 프로그램을 구현하시오.
# 예시 입출력
# words = ["fast", "zero", "base", "study", "baseball", "steel"]
# queries = ["fa", "ba", "zer", "st", "sti"]
# 출력: [1, 2, 1, 2, 0]
class Node:
def __init__(self):
self.children = dict()
self.count = 0
class Trie:
def __init__(self):
self.root = Node()
def add_word(self, word):
curr = self.root
for c in word:
curr.count += 1
if c not in curr.children:
curr.children[c] = Node()
curr = curr.children[c]
curr.children['*'] = Node()
def search(self, query):
curr = self.root
for c in query:
if c not in curr.children:
return 0
curr = curr.children[c]
return curr.count
def solution(words, queries):
trie = Trie()
for word in words:
trie.add_word(word)
result = []
for query in queries:
result.append(trie.search(query))
return result
if __name__ == '__main__':
words = ["fast", "zero", "base", "study", "baseball", "steel"]
queries = ["fa", "ba", "zer", "st", "sti"]
sol = solution(words, queries)
print(sol)3) 와일드카드 검색기2, 검색할 단어가 리스트 words에 주어져 있다. 이번에는 queries의 검색 단어가 와일드카드 ?를 포함하고 있다. 모든 검색 단어는 마지막에 최소 한개의 ?를 가지고 있으며, ?의 개수만큼 아무 문자나 매칭이 가능하다. 이 프로그램을 구현하시오.
# 예시 입출력
# words = ["fast", "zero", "base", "study", "baseball", "steel"]
# queries = ["fa??", "ba??", "ze?", "st???", "z???"]
# 출력: [1, 1, 0, 2, 1]
class Node:
def __init__(self):
self.children = dict()
self.count = 0
class Trie:
def __init__(self):
self.root = Node()
def add_word(self, word):
curr = self.root
for c in word:
curr.count += 1
if c not in curr.children:
curr.children[c] = Node()
curr = curr.children[c]
curr.children['*'] = Node()
def search(self, query):
curr = self.root
for c in query:
if c not in curr.children:
return 0
curr = curr.children[c]
return curr.count
def solution(words, queries):
tries = dict()
for word in words:
n = len(word)
if n not in tries:
tries[n] = Trie()
tries[n].add_word(word)
result = []
for query in queries:
n = len(query)
if n not in tries:
result.append(0)
else:
q = query[:query.index('?')]
result.append(tries[n].search(q))
return result
if __name__ == '__main__':
words = ["fast", "zero", "base", "study", "baseball", "steel"]
queries = ["fa??", "ba??", "ze?", "st???", "z???"]
sol = solution(words, queries)
print(sol)이 글은 제로베이스 데이터 취업 스쿨의 강의 자료 일부를 발췌하여 작성되었습니다