Clustering

📌 K-Means 클러스터링 정리

• 비지도 학습 알고리즘으로 데이터를 K개의 그룹으로 묶음
• 각 데이터 포인트를 가장 가까운 클러스터 중심(centroid)으로 할당
• k-means++ 초기화 방식이 성능이 좋음

---

✅ Elbow Method로 최적의 K 찾기

import numpy as np
import matplotlib.pyplot as plt
from sklearn.cluster import KMeans
from sklearn.datasets import load_iris

# 데이터 로드
iris = load_iris()
X = iris.data

wcss = []  # WCSS(Within-Cluster Sum of Squares)

for k in range(1, 11):
    kmeans = KMeans(n_clusters=k, random_state=42)
    kmeans.fit(X)
    wcss.append(kmeans.inertia_)

plt.figure(figsize=(8, 6))
plt.plot(range(1, 11), wcss, marker='o', linestyle='--')
plt.title('Elbow Method for Optimal K')
plt.xlabel('Number of Clusters')
plt.ylabel('WCSS')
plt.show()

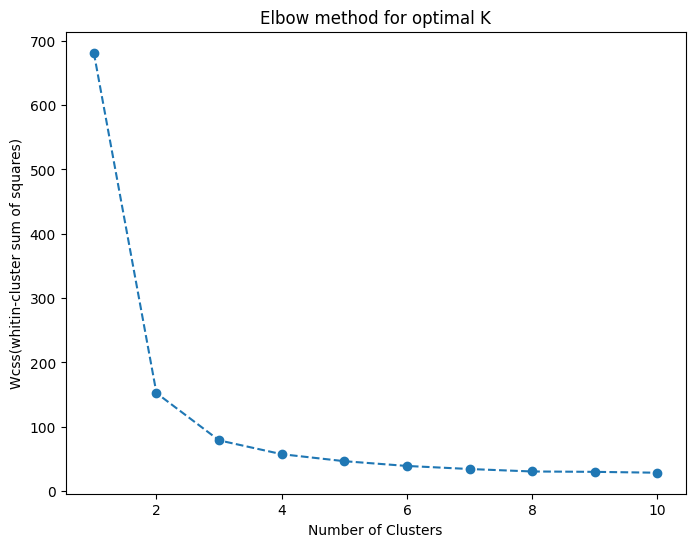
• elbow method: 급격한 감소가 완만해지는 지점이 최적의 클러스터 수
• 비지도 학습에서는 Elbow Method가 유용하지만 절대적인 기준은 아님

---

✅ 최적 K 값으로 K-Means 적용

optimal_k = 3
kmeans = KMeans(n_clusters=optimal_k, random_state=42)
kmeans.fit(X)
y_kmeans = kmeans.predict(X)

• 지도학습과의 차이점: fit(X)만 수행 (y 없음)
• 평가를 직접 할 수 없지만, 데이터셋이 레이블을 제공하면 평가 가능

---

📊 군집 평가 지표

1️⃣ Homogeneity Score

• 동일한 클래스를 가진 데이터들이 동일한 클러스터에 얼마나 잘 분배되었는지
• 1에 가까울수록 좋음

from sklearn.metrics import homogeneity_score

homogeneity = homogeneity_score(iris.target, y_kmeans)
print(f'Homogeneity Score : {homogeneity:.4f}')

---

2️⃣ Completeness Score

• 동일한 클러스터에 속한 데이터들이 실제로 동일한 클래스를 얼마나 잘 보존하는지
• 1에 가까울수록 좋음

from sklearn.metrics import completeness_score

completeness = completeness_score(iris.target, y_kmeans)
print(f'Completeness Score : {completeness:.4f}')

---

3️⃣ V-Measure Score

• Homogeneity + Completeness를 종합적으로 평가하는 지표
• 0~1 사이 값이며, 1에 가까울수록 좋음

from sklearn.metrics import v_measure_score

v_measure = v_measure_score(iris.target, y_kmeans)
print(f'V-Measure Score : {v_measure:.4f}')

---

4️⃣ Adjusted Rand Index (ARI)

• 군집화 결과와 실제 레이블 간 유사성 평가
• 1에 가까울수록 좋음, 0이면 무작위 군집화와 비슷함

from sklearn.metrics import adjusted_rand_score

ari = adjusted_rand_score(iris.target, y_kmeans)
print(f'Adjusted Rand Score : {ari:.4f}')

---

5️⃣ Silhouette Score (실루엣 점수)

• 군집 간 분리도와 군집 내 응집도를 평가
• 1에 가까울수록 군집화가 잘됨
• 0이면 군집이 겹쳐 있음, 음수면 잘못된 군집화

from sklearn.metrics import silhouette_score

silhouette_avg = silhouette_score(X, y_kmeans)
print(f'Silhouette Score : {silhouette_avg:.4f}')

---

6️⃣ Calinski-Harabasz Index

• 클러스터 내 분산과 클러스터 간 분산을 고려하여 군집 품질 평가
• 값이 클수록 군집화 품질이 좋음

from sklearn.metrics import calinski_harabasz_score

calinski_harabasz = calinski_harabasz_score(X, y_kmeans)
print(f'Calinski-Harabasz Score : {calinski_harabasz:.4f}')

---

7️⃣ Dunn Index

• 클러스터 간 거리 대비 클러스터 내 거리의 비율
• 값이 클수록 군집화 품질이 좋음

from scipy.spatial.distance import cdist

def dunn_index(X, labels):
    cluster_centers = np.array([X[labels == i].mean(axis=0) for i in np.unique(labels)])
    intra_cluster_distances = np.array([np.max(cdist(X[labels == i], [cluster_centers[i]])) for i in np.unique(labels)])
    inter_cluster_distances = np.array([[np.linalg.norm(cluster_centers[i] - cluster_centers[j]) for j in range(len(cluster_centers))] for i in range(len(cluster_centers))])
    np.fill_diagonal(inter_cluster_distances, np.inf)
    
    return np.min(inter_cluster_distances) / np.max(intra_cluster_distances)

dunn_idx = dunn_index(X, y_kmeans)
print(f'Dunn Index : {dunn_idx:.4f}')

---

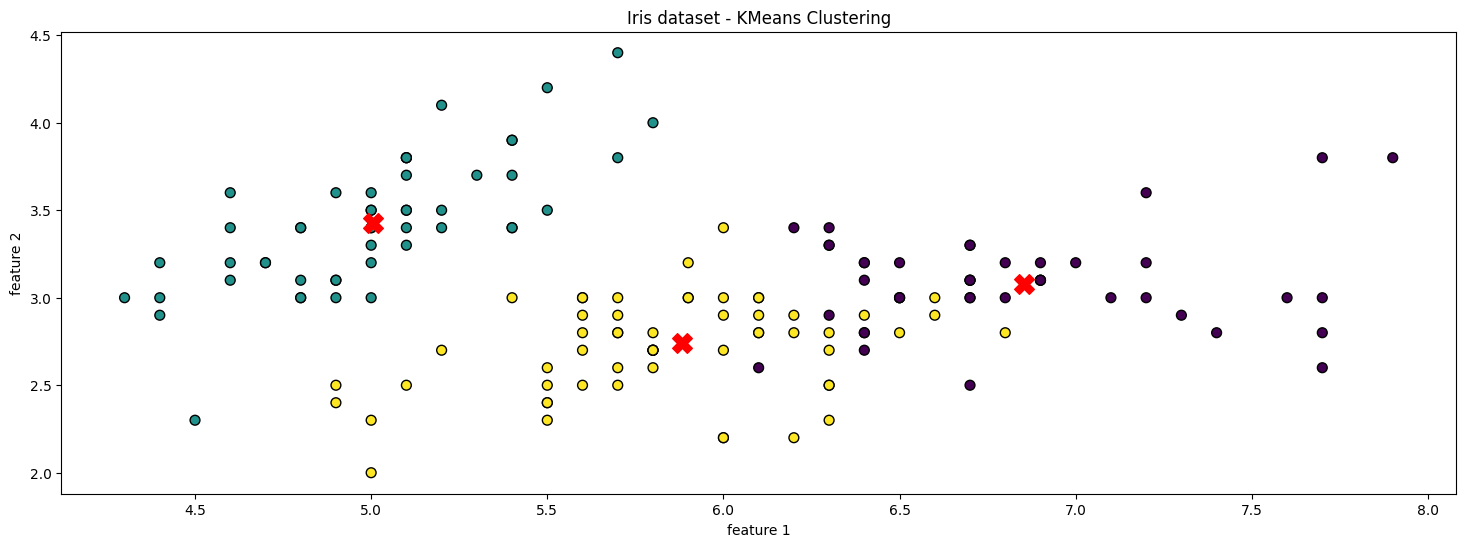
📌 K-Means 군집 시각화

import matplotlib.pyplot as plt

plt.figure(figsize=(8, 6))
plt.scatter(X[:, 0], X[:, 1], c=y_kmeans, cmap='viridis', edgecolors='k', s=50)

# KMeans 클러스터 중심 표시
plt.scatter(kmeans.cluster_centers_[:, 0], kmeans.cluster_centers_[:, 1], s=200, c='red', marker='X')
plt.title('Iris Dataset - KMeans Clustering')
plt.xlabel('Feature 1')
plt.ylabel('Feature 2')
plt.show()

---

scores

Homogeneity Score :  0.7364
completeness score : 0.7475
v_measure score : 0.7419
adjusted_rand_score : 0.7163
silhouette score 0.5512
Dunn Index : 1.0860

---

📝 정리

• Elbow Method로 최적의 클러스터 수 찾음
• Silhouette Score와 함께 군집 품질 평가
• K-Means는 이상치(outlier)에 민감함
• 비지도 학습이므로 라벨이 없으면 직접 라벨링 필요
• silhouette_score, elbow method 두 개가 가장 많이 사용됨