K-Means 클러스터링 정리
- K-Means는 데이터를 K개의 그룹으로 묶는 비지도 학습 알고리즘임
- 클러스터 중심(centroid)을 기준으로 데이터를 군집화함
- 초기 중심점 설정이 중요하며,
k-means++방식이 일반적임
K-Means 적용 코드
import mglearn
import numpy as np
import matplotlib.pyplot as plt
from sklearn.cluster import KMeans
from sklearn.datasets import make_blobs
# 데이터 생성
X, y = make_blobs(random_state=42)
# KMeans 클러스터링 (3개 군집)
kmeans = KMeans(n_clusters=3)
kmeans.fit(X)
# 군집 라벨 출력
print(kmeans.labels_)
# 데이터 시각화
mglearn.discrete_scatter(X[:, 0], X[:, 1], kmeans.labels_, markers='o')
mglearn.discrete_scatter(
kmeans.cluster_centers_[:, 0], kmeans.cluster_centers_[:, 1], [0, 1, 2],
markers='^', markeredgewidth=2)
plt.show()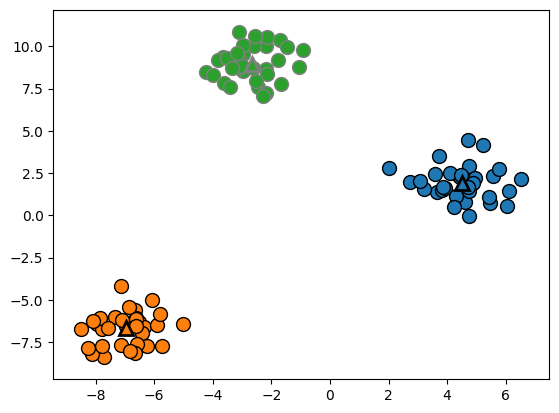
K 값 변화에 따른 군집화
- 클러스터 개수를 바꾸면 결과가 달라짐
- 3개 vs 5개 클러스터 비교
fig, axes = plt.subplots(1, 2, figsize=(10, 5))
# K=3
kmeans = KMeans(n_clusters=3)
kmeans.fit(X)
assignments = kmeans.labels_
mglearn.discrete_scatter(X[:, 0], X[:, 1], assignments, ax=axes[0])
# K=5
kmeans = KMeans(n_clusters=5)
kmeans.fit(X)
assignments = kmeans.labels_
mglearn.discrete_scatter(X[:, 0], X[:, 1], assignments, ax=axes[1])
plt.show()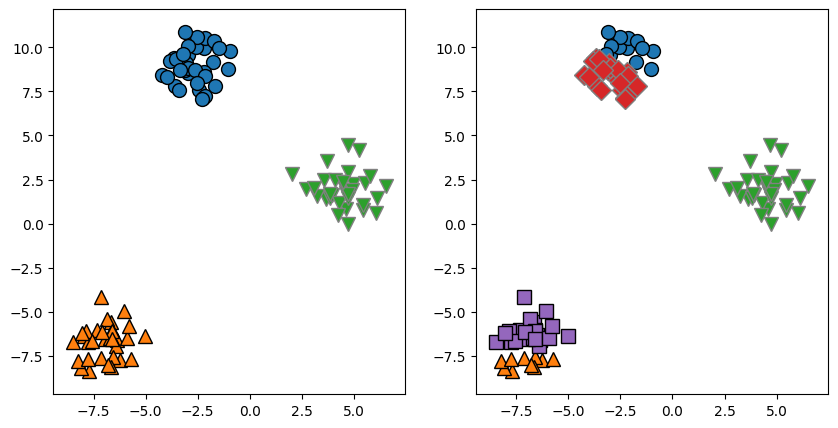
클러스터링이 잘 안 되는 경우
- 데이터가 퍼져있으면 클러스터링 성능 저하
- 아래와 같이 변형된 데이터에서는 K-Means가 적절하지 않음
X_varied, y_varied = make_blobs(n_samples=200,
cluster_std=[1.0, 2.5, 0.5],
random_state=170)
y_pred = KMeans(n_clusters=3, random_state=0).fit_predict(X_varied)
mglearn.discrete_scatter(X_varied[:, 0], X_varied[:, 1], y_pred)
plt.legend(["cluster 0", "cluster 1", "cluster 2"], loc='best')
plt.xlabel("atrr 0")
plt.ylabel("atrr 1")
plt.show() # 책에는 없음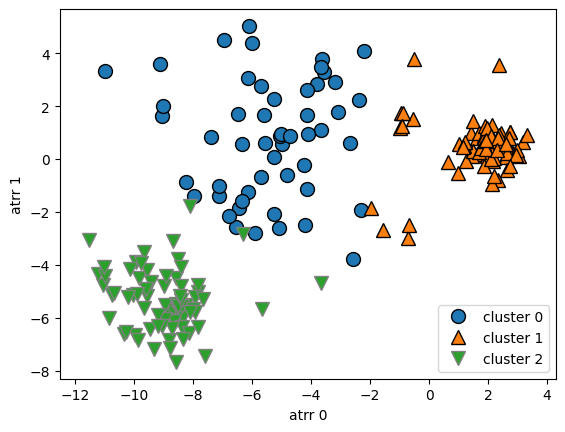
import numpy as np
# 무작위로 클러스터 데이터 생성합니다
X, y = make_blobs(random_state=170, n_samples=600)
rng = np.random.RandomState(74)
# 데이터가 길게 늘어지도록 변경합니다
transformation = rng.normal(size=(2, 2))
X = np.dot(X, transformation)
# 세 개의 클러스터로 데이터에 KMeans 알고리즘을 적용합니다
kmeans = KMeans(n_clusters=3)
kmeans.fit(X)
y_pred = kmeans.predict(X)
# 클러스터 할당과 클러스터 중심을 나타냅니다
mglearn.discrete_scatter(X[:, 0], X[:, 1], kmeans.labels_, markers='o')
mglearn.discrete_scatter(
kmeans.cluster_centers_[:, 0], kmeans.cluster_centers_[:, 1], [0, 1, 2],
markers='^', markeredgewidth=2)
plt.xlabel("특성 0")
plt.ylabel("특성 1")
plt.show() # 책에는 없음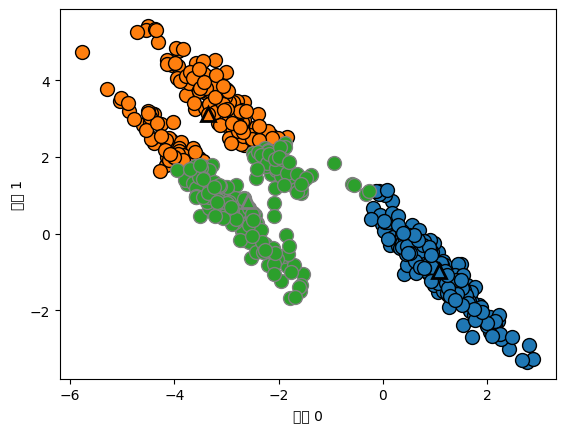
from sklearn.datasets import make_moons
X, y = make_moons(n_samples=200, noise=0.05, random_state=0)
# K=2로 클러스터링
kmeans = KMeans(n_clusters=2)
kmeans.fit(X)
y_pred = kmeans.predict(X)
# 시각화
plt.scatter(X[:, 0], X[:, 1], c=y_pred, cmap=mglearn.cm2, s=60, edgecolors='k')
plt.scatter(kmeans.cluster_centers_[:, 0], kmeans.cluster_centers_[:, 1],
marker='^', c=[mglearn.cm2(0), mglearn.cm2(1)], s=100, linewidth=2, edgecolors='k')
plt.xlabel("attr 0")
plt.ylabel("attr 1")
plt.show()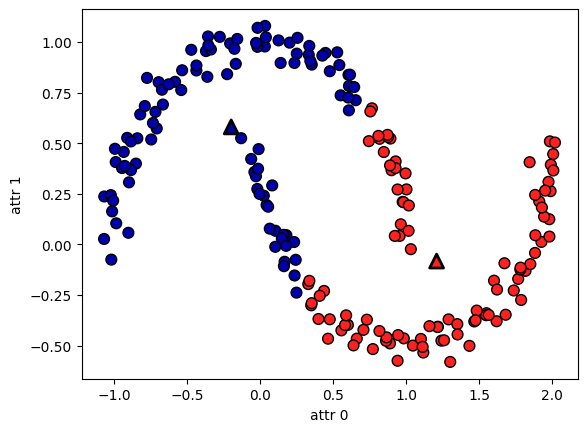
K-Means 성능 평가
- 여러 가지 평가 지표 존재
- 대표적인 지표: Silhouette Score, Calinski-Harabasz Score, V-measure 등
from sklearn.metrics import silhouette_score, calinski_harabasz_score, homogeneity_score, completeness_score, v_measure_score, adjusted_rand_score, rand_score
from sklearn.preprocessing import StandardScaler
from sklearn.datasets import load_iris
# 데이터 로드 및 표준화
iris = load_iris()
X = iris.data
scaler = StandardScaler()
X_std = scaler.fit_transform(X)
# KMeans 클러스터링
km = KMeans(n_clusters=3, init="k-means++", max_iter=100, n_init=1)
km.fit(X_std)
# 평가 지표 출력
print("Silhouette Coefficient: %.3f" % silhouette_score(X_std, km.labels_))
print("Calinski and Harabasz score: %.3f" % calinski_harabasz_score(X_std, km.labels_))
print("Homogeneity: %.3f" % homogeneity_score(iris.target, km.labels_))
print("Completeness: %.3f" % completeness_score(iris.target, km.labels_))
print("V-measure: %.3f" % v_measure_score(iris.target, km.labels_))
print("Rand-Index: %.3f" % rand_score(iris.target, km.labels_))
print("Adjusted Rand-Index: %.3f" % adjusted_rand_score(iris.target, km.labels_))적절한 K 값 찾기
- K 값이 너무 작거나 크면 군집화가 부적절할 수 있음
- Elbow Method를 사용해서 적절한 K 찾기
Objectives = []
K = range(2, 15)
for k in K:
km = KMeans(n_clusters=k)
km.fit(X_std)
Objectives.append(km.inertia_)
plt.plot(K, Objectives, 'bx-')
plt.xlabel('Number of clusters')
plt.ylabel('Objective Function Value')
plt.show()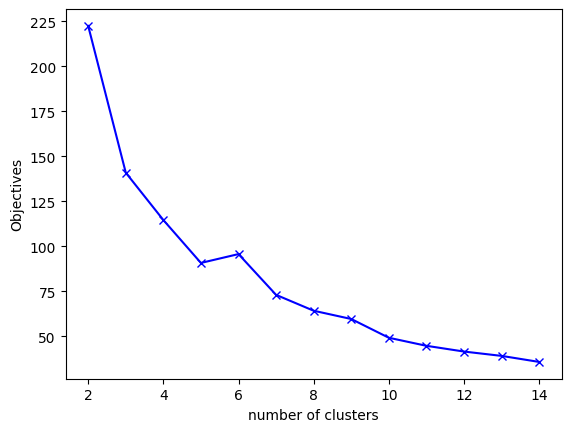
경사가 완만해지기 전이라 생각
K-Means 특징 요약
-
장점
- 대규모 데이터에 빠르게 적용 가능
- 해석이 직관적임
-
단점
- 이상치에 매우 민감
- 군집 개수를 미리 정해야 함
- 클러스터의 모양이 원형이 아니면 성능이 저하됨
