PCA(주성분 분석, Principal Component Analysis)

1. 개요

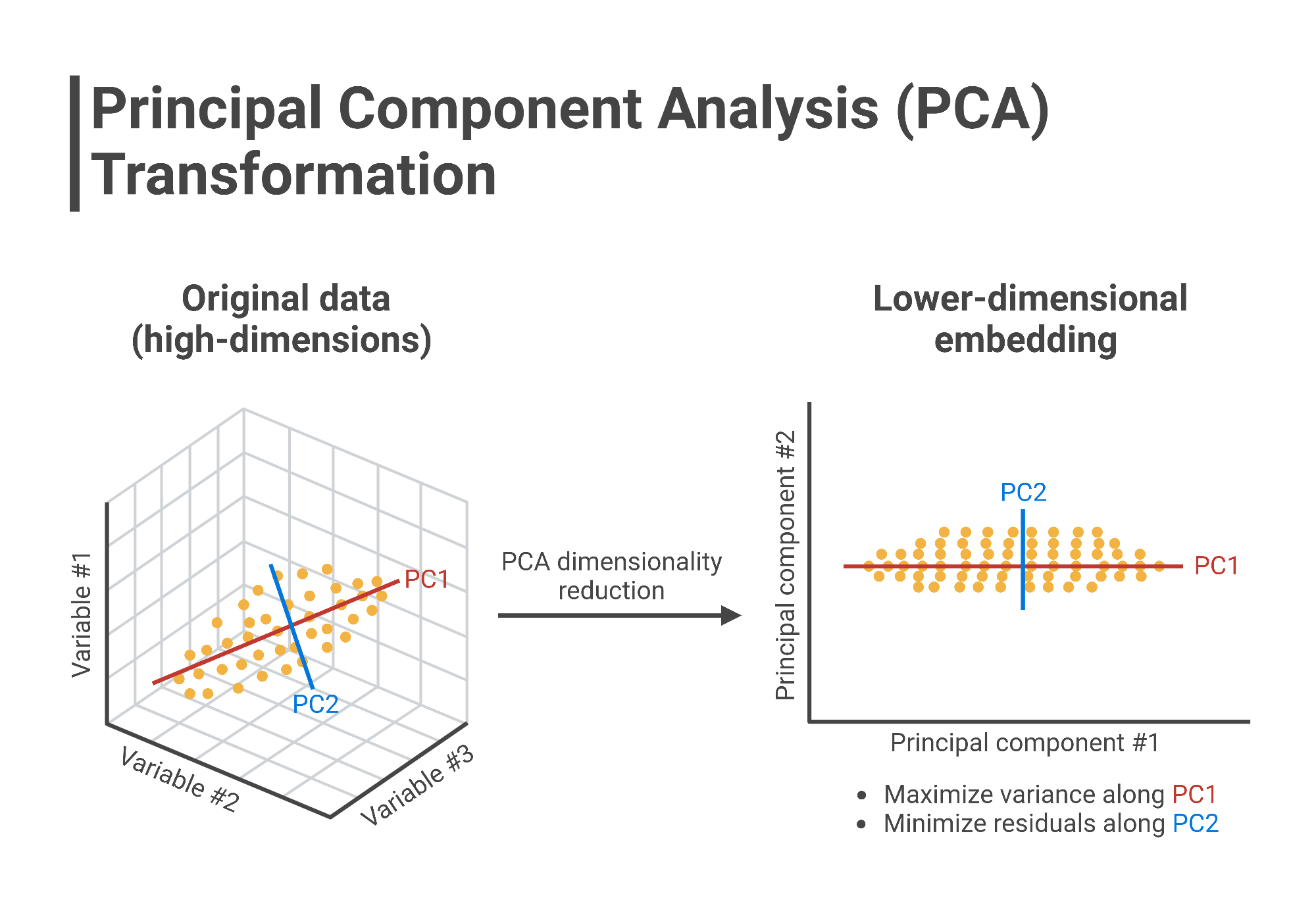
• PCA(Principal Component Analysis, 주성분 분석)는 고차원 데이터를 저차원으로 변환하는 차원 축소 기법
• 데이터의 중요한 특성을 유지하면서도 차원을 줄여 분석의 효율성을 높이고, 시각화를 용이하게 하는 데 사용
• PCA는 비지도 학습(Unsupervised Learning) 방식으로 작동하며, 데이터의 분산(Variance)이 최대가 되는 새로운 축(주성분)을 찾아 데이터를 투영(projection)하는 방법

---

2. 개념

2.1 차원 축소

• 고차원 데이터는 시각화가 어렵고 연산 비용이 크며 다중 공선성 문제가 발생함.
• PCA를 통해 차원을 줄이면 데이터의 핵심 정보를 유지하면서도 분석을 더 효율적으로 수행할 수 있음.

2.2 주성분

• PCA는 원본 데이터에서 서로 직교하는 새로운 축(주성분, Principal Components)을 찾아 데이터를 변환함.
• 각 주성분은 데이터의 분산을 최대한 보존하는 방향으로 정해짐.
• 주성분은 원본 데이터의 선형 결합(Linear Combination)으로 표현되며, 일반적으로 처음 몇 개의 주성분만 사용하여 데이터 차원을 축소함.

2.3 공분산 행렬과 분산 설명

• PCA는 공분산 행렬을 이용해 변수 간의 상관관계를 분석하고, 데이터의 주 방향(분산이 가장 큰 방향)을 찾음.
• 각 주성분이 전체 데이터 분산에서 차지하는 비율을 설명된 분산(Explained Variance)이라고 함.

---

3. 수행 과정

3.1 데이터 정규화

• 각 변수의 스케일이 다르면 PCA 결과에 영향을 줄 수 있기 때문에, 평균을 0, 분산을 1로 맞추는 표준화(Standardization)를 진행함.

3.2 공분산 행렬 계산

• 데이터의 분포를 분석하기 위해 공분산 행렬을 계산함.

3.3 고유값과 고유벡터 계산

• 공분산 행렬에서 고유값(Eigenvalues)과 고유벡터(Eigenvectors)를 계산함.
• 고유값이 큰 방향이 데이터의 주 방향(주성분)이며, 고유벡터는 해당 방향의 좌표축을 나타냄.

3.4 주성분 선택

• 고유값이 큰 순서대로 주성분을 선택함.
• 설명된 분산 비율을 보고, 원하는 차원까지 축소할 수 있음.

3.5 데이터 변환

• 원본 데이터를 선택한 주성분 공간으로 변환함.

---

4. 장점과 한계

4.1 장점

• ✅ 차원 축소 효과: 고차원 데이터를 저차원으로 변환하여 연산 속도를 개선하고 시각화를 가능하게 함.
• ✅ 노이즈 제거 기능: 중요하지 않은 특징을 제거하여 데이터의 핵심 패턴을 더 잘 파악할 수 있음.
• ✅ 자동 특징 선택: 수동으로 변수를 선택하는 대신, 주성분을 통해 데이터의 핵심 정보를 자동으로 추출할 수 있음.

4.2 한계

• ❌ 해석의 어려움: 변환된 주성분은 원본 변수와 다르기 때문에 해석이 어려울 수 있음.
• ❌ 선형 관계만 표현 가능: PCA는 선형적인 방법이므로, 비선형적인 관계를 잘 표현하지 못함.
• ❌ 정보 손실 가능성: 너무 많은 차원을 제거하면 중요한 정보가 손실될 수 있음.

---

5. 응용 사례

5.1 이미지 압축

• PCA는 이미지 데이터를 저차원으로 변환하여 저장 공간을 절약하면서도 원본 이미지와 유사한 품질을 유지하는 데 활용됨.
• 얼굴 인식(Face Recognition)에서 Eigenfaces(고유 얼굴) 기법이 대표적인 예시임.

5.2 데이터 시각화

• 고차원 데이터를 2차원 또는 3차원으로 축소하여 시각화할 때 사용됨.
• 유전자 데이터 분석, 고객 분류 등의 문제에서 유용함.

5.3 노이즈 제거

• 센서 데이터나 신호 처리에서 노이즈를 제거하고 주요 신호만 유지하는 데 사용됨.

5.4 금융 데이터 분석

• 주가 변동성을 설명하는 주요 요인을 찾거나, 시장 데이터를 요약하는 데 활용됨.

---

6. 결론

• PCA는 데이터의 주요 특성을 유지하면서 차원을 줄이는 강력한 기법임.
• 특히 데이터 시각화, 노이즈 제거, 머신러닝 모델 성능 향상 등에 유용함.
• 하지만 해석이 어려울 수 있으며, 선형 변환만 가능하다는 한계를 고려해야 함.
• PCA를 적절히 활용하면 복잡한 데이터에서도 핵심적인 패턴을 찾을 수 있음.