목표

파이토치로 MLP(Multi-Layer Perceptron, 여러 층으로 구성된 인공신경망)모델을 시각화해보자.

MLP는 다중회귀(Multiple Linear Regreesion)과 닮았으므로 이를 활용해보자.

• 라이브러리 import | 파이토치 핵심 라이브러리
• 비선형 데이터 생성| 텐서 연산 시 주의사항(차원 변경-squeeze, unsqueeze)
• 모델 정의 | 신경망 클래스의 은닉층과 활성화 함수 갯수 정의
• 손실함수 & 옵티마이저 | 손실함수 종류 및 옵티마이저 세부 조정
• 모델 학습 | 에폭, 기울기 초기화, 손실/미분/가중치
• 예측 | output 차원 변경, 예측값 생성
• 시각화 | 추세선
  

🔍 MLP란?

MLP는 Multi-Layer Perceptron으로, 여러 층으로 구성된 인공신경망(Artificial Neural Network)이다.
-Multi-Layer : 여러 층 (입력층, 은닉층, 출력층)
-Perceptron : 뉴런 하나에 해당하는 기본 단위 연산 (가중치 곱 + 편향 + 활성화 함수)

y = f(W2 * f(W1 * x + b1) + b2)

• x: 입력 (벡터)
• W1, W2: 가중치 행렬
• b1, b2: 편향
• f(): 비선형 함수 (예: ReLU, sigmoid 등)

📌 이 구조는 다중 회귀(Multiple Linear Regression) 와 아주 닮았다.

다중 회귀 vs 신경망(Multi-Layer Perceptrion)

📌 다중 회귀는 신경망의 가장 기초 형태 로 봐도 무방하다.
➡️ 다중 회귀 : 직선, 평면, 초평면
➡️ MLP : 곡선, 계단, 꺾임 등을 자유자재로 학습할 수 있음
➡️ MLP : 다중회귀보다 훨씬 강력한 표현력을 가진다

PyTorch의 장점

GPU 연산과 자동 미분(autograd)가 가능하며, 모듈화된 모델 구조를 이용할 수 있어서, MLP구현도 쉽고, 이후 CNN, RNN 확장도 간단하다.

0. Library import

import torch                      # PyTorch 핵심 라이브러리 (텐서, 연산, 모델 구성 등)
import torch.nn as nn             # 신경망 모델 구성 (nn.Linear, nn.ReLU 등)
import torch.optim as optim       # 옵티마이저 (파라미터 업데이트 알고리즘)
import matplotlib.pyplot as plt   # 시각화 도구 (데이터, 예측 결과 plot용)

1. 데이터 생성

x = torch.linspace(-10, 10, 100)            # x값: -10부터 10까지 균등하게 100개 생성 (1차원 텐서)
noise = 0.3 * torch.randn(100)              # 노이즈: 표준정규분포에서 100개 샘플, 크기 0.3배
y = torch.sin(x) + noise                    # 정답 y: sin 곡선 + 노이즈 (비선형 함수)

X_tensor = x.unsqueeze(1)                   # shape: (100,) → (100, 1), MLP 입력을 위해 2차원으로
y_tensor = y.unsqueeze(1)                   # shape: (100,) → (100, 1), MLP 출력과 비교 위해 2차원으로

📌 unsqueeze(1)은 MLP가 (batch_size, feature)의 행렬 구조 형식만 받기 때문에 꼭 필요하다.
🔍 왜 모델학습 전 unsqueeze를 먼저해줬는가? 내가 쓸 신경망 모델 Pythoch의 nn.Linear는 2차원 텐서를 입력받는다.

nn.Linear(1, 64)

L 위는 입력이 1개짜리인 뉴런이 64개 있는 은닉층.
L 한 번에 여러 개의 샘플(batch)을 넣고,그 각각이 1차원 벡터(즉, 특징이 1개짜리)여야 함.
L 그런데 x = torch.linspace(-10, 10, 100) 는 숫자 100개 일렬로 있는 1차원 벡터임.

📌 x에 unsqueeze(1) 을 하는 이유

X_tensor = x.unsqueeze(1)    # shape: (100,) → (100, 1)

unsqueeze(1)은 두 번째 차원(feature 차원)을 만들어줘서,100개의 샘플이 각각 [x] 모양의 행으로 있는 2차원 텐서가 됨.

📌 y에 unsqueeze(1) 을 하는 이유

y_tensor = x.unsqueeze(1)    # shape: (100,) → (100, 1)

예측값이 (100, 1)이 되기 때문에, 비교 대상인 실제값 y도 (100, 1) 로 만들어줘야 손실 함수에서 오류가 안난다. 손실 함수(MSELoss)는 shape이 정확히 일치해야 비교 가능하다.

📌 루프 안에서 처리하지 않고, 데이터 생성 시 처리한 이유
학습 전에 미리 처리해두면 코드가 깔끔하고, 실수도 줄고, 재사용도 쉬워진다. 이후 X_tensor만 모델에 넣으면 되기 때문이다.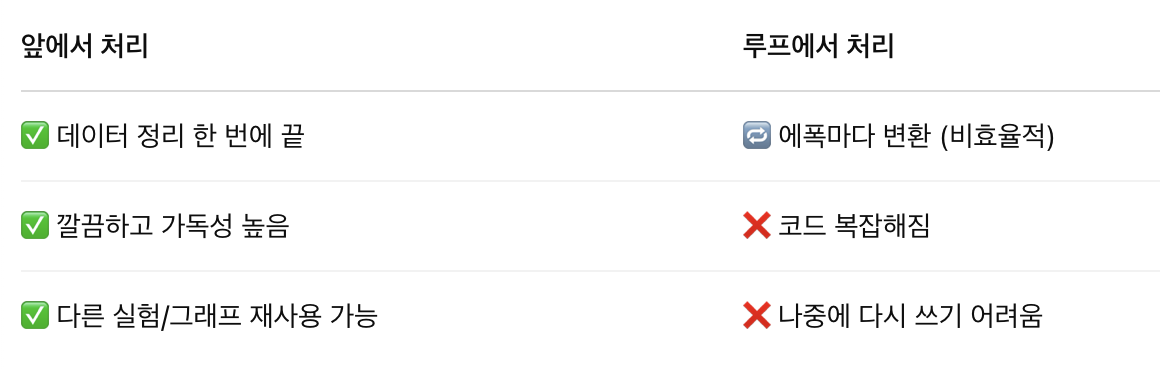

2. 모델 정의 - MLP 클래스

class BalancedMLP(nn.Module):               # PyTorch의 신경망 클래스 상속
    def __init__(self):
        super().__init__()                  # 상속받은 초기화 설정

        self.model = nn.Sequential(         # Sequential: 레이어들을 순서대로 쌓은 구조
            nn.Linear(1, 64),               # 입력 1개 → 첫 은닉층 64개 뉴런
            nn.ReLU(),                      # 비선형 함수 (활성화 함수)
            nn.Linear(64, 64),              # 은닉층 64 → 은닉층 64
            nn.ReLU(),                      # 비선형성 추가 (그래야 곡선 표현 가능)
            nn.Linear(64, 1)                # 마지막 은닉층 64 → 출력 1개 (예측값)
        )

    def forward(self, x):
        return self.model(x)                # 입력 x가 들어오면 위에 정의한 모델에 넣음

✅ ReLU : 비선형 활성화 함수. 입력값이 0보다 크면 그대로 통과, 0 이하면 0으로 잘라버림.
✅ 만약 ReLU 없이 Linear → Linear → Linear만 쌓으면?
👉 그냥 하나의 Linear 함수로 합쳐지므로, 층을 쌓아도 여전히 선형 모델이다.
👉 그래서 반드시 중간에 비선형 함수(ReLU, tanh 등) 를 넣어야 직선으로는 못 푸는 문제 (곡선, 계단 등) 도 풀 수 있다.
🎯 즉, ReLU 덕분에 MLP는 sin(x), 곡선, 계단, 꺾이는 함수 등 복잡한 형태를 학습할 수 있다.

Linear(1, 64)
Linear(64, 64)
Linear(64, 1)

👉 ReLU는 간단하고 빠르면서도 효과 좋으며, 딥러닝에서 기본은 ReLU이다.

📊 예시 비교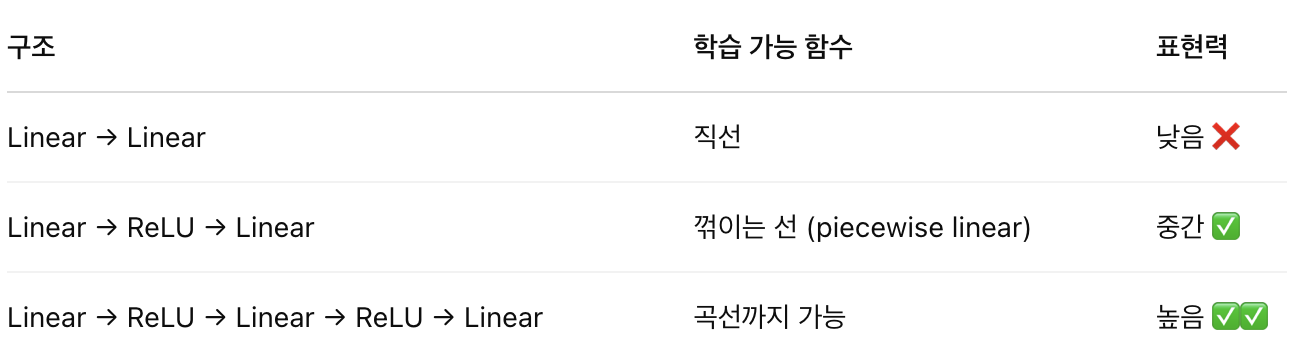

3. 손실 함수 & 옵티마이저

model = BalancedMLP()                                    # 모델 인스턴스 생성

optimizer = optim.Adam(model.parameters(), lr=0.01)      # Adam 옵티마이저, 학습률 0.01
loss_func = nn.MSELoss()                                 # MSE 손실함수: 예측값과 실제값 차이 제곱 평균

- 옵티마이저 : Adam 사용

손실을 줄이기 위해 모델의 파라미터(w, b 등) 를 업데이트하는 알고리즘
🔹 Adam: 빠르고 자동조정 가능해서 대부분의 상황에서 기본값 (Adaptive Moment Estimation)
🔹 SGD: 단순하고 가볍지만, 튜닝이 필요하고 학습이 느릴 수 있음 (확률적 경사 하강법)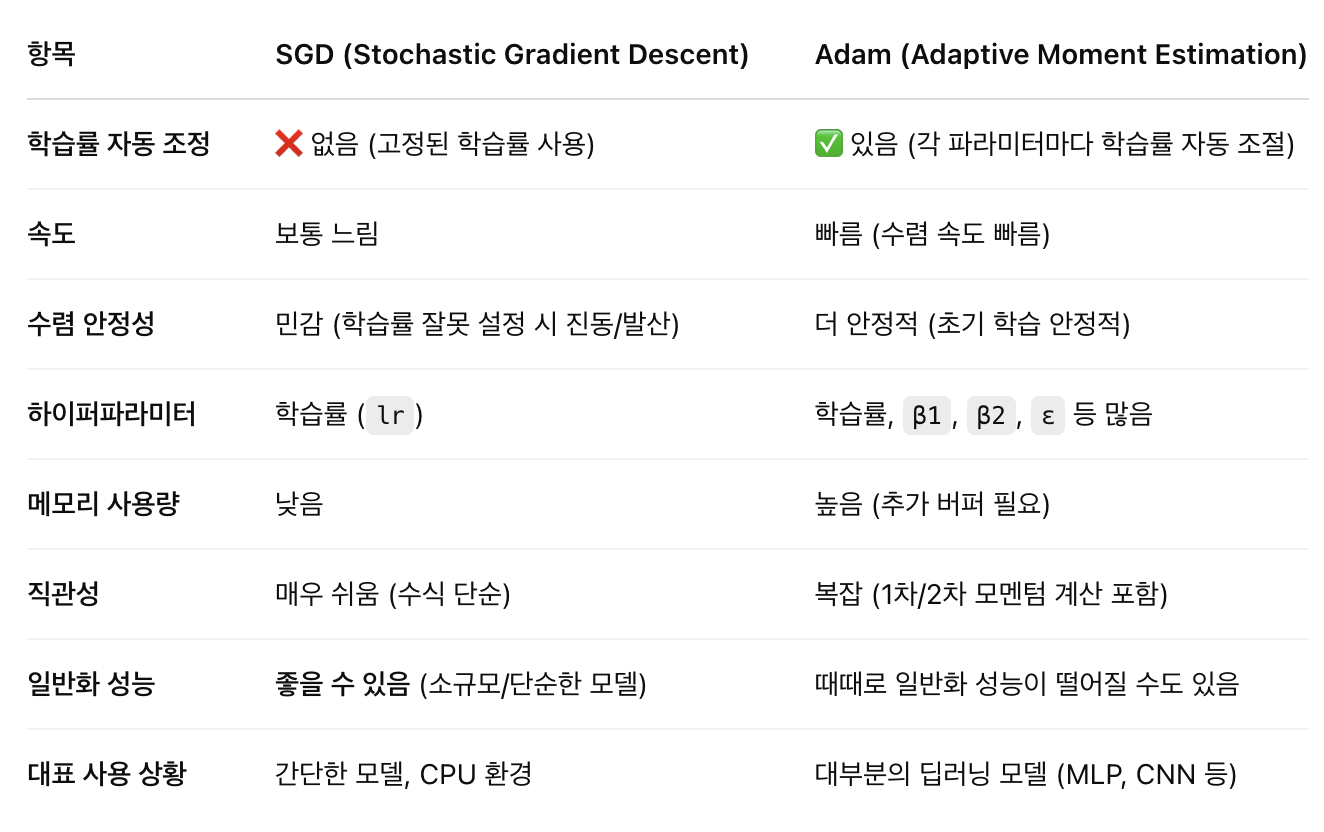
Adam은

• 1차 모멘텀(m): 이전 gradient의 평균 → 속도
• 2차 모멘텀(v): gradient 제곱의 평균 → 방향 안정성 을 추적
  📌 각 파라미터마다 다르게, 적응적으로 학습률 조정함. 덕분에 초기 학습 빠르고, 학습률 튜닝도 덜 예민함.

✅ 언제 어떤 옵티마이저를 써야할까?

- 학습률 lr=0.01 사용

학습할 때 가중치를 얼마나 크게 움직일지를 결정하는 값 (즉, 경사하강법에서 얼마나 크게 점프할지를 의미함)
너무 크면 튀고, 너무 작으면 느림. 0.01은 일반적으로 좋은 시작점이다.

• lr=0.01은 빠르게 학습되지만 불안정,
• lr=0.001은 느리지만 더 정밀하고 안정적이에요.
• 처음엔 빠르게 0.01로, 잘 되면 0.001로 다듬는 게 베스트 전략

✅ 학습률이 0.01일 때 vs 0.001일 때

✅ 언제 어떤 학습률이 좋을까?

✅ 보통 Adam에선 0.001,SGD에선 0.01 또는 더 작게 시작하기도 한다.
✅ 학습률을 초기에 크게, 이후 작게 줄이는 것도 많이 쓴다
👉 learning rate scheduler (예: StepLR, ReduceLROnPlateau 등)

- 손실함수 MSELoss 사용

MSE = Mean Squared Error(평균 제곱 오차)로 예측값과 실제값 사이의 차이(오차)를 제곱해서 평균 낸 값.
회귀 문제에서 가장 많이 쓰는 손실함수
✅ 왜 제곱을 할까?
예측값이 너무 멀리 떨어지면 오차를 더 크게 벌점 주기 위해, 마이너스가 상쇄되지 않게 절대값 대신 제곱 사용.

loss_fn = nn.MSELoss()
loss = loss_fn(y_pred, y_true)

4. 모델학습 (Traning loop)

loss_list = []  # 에폭마다 손실값(loss)을 저장할 리스트를 만들어둠

📌 학습이 진행될수록 손실(loss)이 줄어드는지 확인하기 위해 매 에폭마다 기록함.
✅ 나중에 plt.plot(loss_list) 해서 그래프로 확인가능하다.

for epoch in range(690):  # 총 690번 반복 = 690번 학습 (epoch: 전체 데이터셋 한 바퀴 학습)

🔁 1 epoch = 한 번 전체 데이터를 모델에 넣고 학습시키는 단위
여기선 690번 전체 데이터를 반복 학습함

optimizer.zero_grad()  # ① 이전에 계산된 기울기(gradient) 초기화

📌 PyTorch는 기본적으로 gradient를 누적해서 계산함. 그래서 매번 backward() 하기 전에 초기화를 꼭 해줘야 함!

output = model(X_tensor)  # ② 입력 X_tensor를 모델에 넣어서 예측값(output)을 얻음

✅ 입력 데이터를 MLP 모델에 넣어서 예측값을 만듦. 예: x값이 들어가면 y값을 예측함.

loss = loss_func(output, y_tensor)  # ③ 예측값과 실제값을 비교해서 손실(loss) 계산

✅ 예측값 output과 실제 정답 y_tensor 사이의 오차 계산
여기서 쓰는 loss_func는 nn.MSELoss() (평균 제곱 오차)

loss.backward()  # ④ 오차를 기준으로 모든 가중치에 대해 미분 → 기울기 계산

📌 손실을 각 파라미터에 대해 미분해서 기울기(gradient)를 계산
📌 이 과정이 역전파(backpropagation) 임

optimizer.step()  # ⑤ 기울기를 이용해 파라미터(가중치) 업데이트

📌 앞서 계산된 기울기를 바탕으로 파라미터를 업데이트해서 학습을 한 걸로 만듦
📌 옵티마이저가 여기서 SGD, Adam 등의 알고리즘을 수행함

loss_list.append(loss.item())  # 손실값(loss)을 리스트에 저장 (item()은 숫자로 꺼내는 함수)

📌 현재 에폭에서의 손실값을 loss_list에 저장
📌 loss.item()은 파이토치 텐서 → 일반 숫자(float)로 변환

5. 예측하기

x_dense = torch.linspace(-10, 10, 300).unsqueeze(1)   # (300,)1차원 텐서 → (300, 1)
y_pred = model(x_dense).detach().squeeze()            # 예측값 생성 (그래디언트 추적 제거 후 1차원으로)

📌 detach(): 예측 시에는 그래디언트 계산 안 함 (메모리 효율)
📌 unsqueeze(1) : MLP 모델은 2차원 입력만 받음 → (배치 크기, 특징 수) 형태
그래서 unsqueeze(1)로 (300,)을 (300, 1)로 바꿔줘야함.

📌 squeeze(): 2차원 텐서 (300, 1) → 1차원 (300,) 으로 줄여줌
✅ 시각화할 때 plt.plot(x, y)는 둘 다 1차원 벡터여야함
그래서 (300, 1)인 예측값을 squeeze()로 (300,)으로 바꿔줌
🎯unsqueeze(1)은 모델에 넣기 위해 차원 늘리고,
🎯squeeze()는 그래프로 그릴 수 있게 차원을 줄여준다.

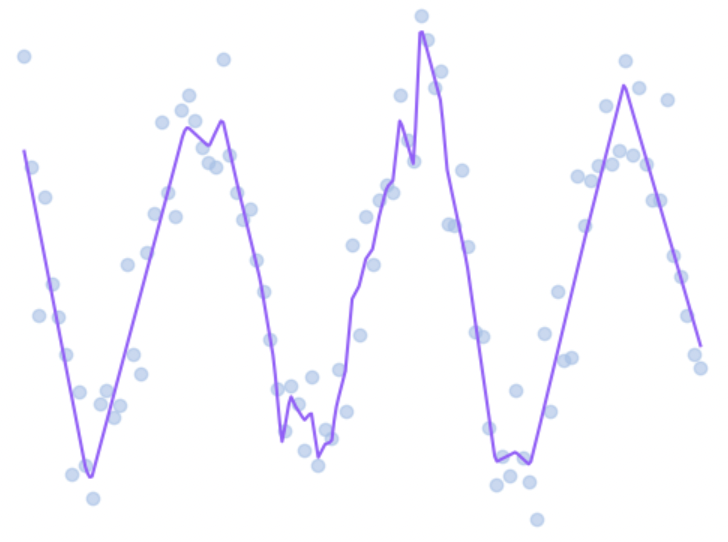
6. 시각화

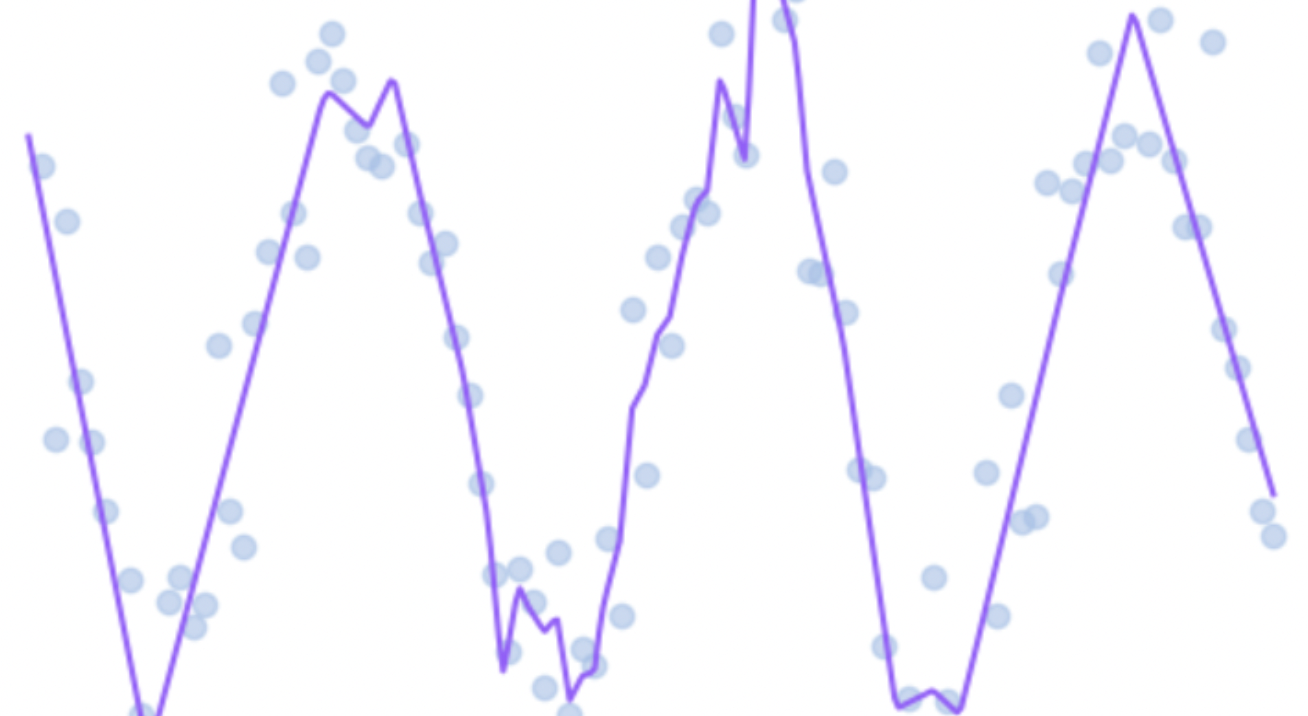
plt.scatter(x.numpy(), y.numpy())   # 원래 데이터 점 찍기 (노이즈 포함된 실제 데이터)
plt.plot(x_dense.numpy(), y_pred.numpy(), color='#')  # 모델이 예측한 부드러운 곡선 
plt.title("Final")
plt.xlabel("x")
plt.ylabel("y")
plt.show()

✅ scatter(): 파란 점 (실제 데이터)
✅ plot(): 빨간 선 (모델 예측 곡선)
✅ x_dense는 x의 "조밀한 샘플"이라 곡선이 부드럽게 나옴